含潜伏时滞效应和非线性发生率的SEIR模型的长时间行为*

杨若晨，马明菊，齐逸飞,李 君

(1. 圣约翰大学托宾商学院, 美国 纽约 NY11439；2. 莆田学院数学学院, 福建 莆田 351100；3. 西北师范大学经济学院,甘肃 兰州 730070；4. 西安电子科技大学, 陕西 西安 710071)



含潜伏时滞效应和非线性发生率的SEIR模型的长时间行为*

杨若晨1，马明菊2，齐逸飞3,李 君4

(1. 圣约翰大学托宾商学院, 美国 纽约 NY11439；2. 莆田学院数学学院, 福建 莆田 351100；3. 西北师范大学经济学院,甘肃 兰州 730070；4. 西安电子科技大学, 陕西 西安 710071)

研究了一类含有潜伏时滞和非线性发生率的SEIR流行病模型。给出了疾病流行的阈值条件，并且得到了无病平衡点和流行病平衡点的局部稳定性条件。通过构造适当的 Lyapunov 泛函, 结合 LaSalle 不变集原理, 证明了当基本再生数R0≤1时,无病平衡点是全局渐近稳定的；但当R0>1时，流行病平衡点是全局渐近稳定的, 同时利用数值模拟验证了分析的结果。

流行病；数学模型；潜伏期；复发；时滞；全局稳定性

在有关传染病模型的文献中, 常常假设疾病的潜伏期是可以忽略的, 基于这种假设的传染病模型被称为是模型, 但是在某些疾病中, 它们的潜伏期是不能被忽略的,例如结核, 流感, 麻疹等[1-2]。感染了相应病菌的染病者在潜伏期内是不具有传染性的, 他们会在发病前有一段潜伏期, 因此在描述这种潜伏期时, 引入时滞的因素是合理的[3-5]。Van den Driessche 和Zou 在文献[6]中指出, 有些康复者会由于休眠致病菌的复原作用而复发成为感染者, 例如人和牛肺结核[7-8], 及弓形体病毒感染[9]等。比率依赖型发生率最早是由Arditi等在文献[10]中引入, 后来由Li等应用于传染病模型中[11]。受文献[6]和文献[11]的启发, 考虑具有潜伏时滞影响的传染病模型。我们将人群分为四类, 其人数分别记作易感者S(t), 处于潜伏期的人E(t), 感染者I(t), 具有短暂免疫者R(t)。

(1)

S(θ)=φ1(θ),E(θ)=φ2(θ),

I(θ)=φ3(θ),R(θ)=φ4(θ)，

φi(θ)≥0,θ∈[-τ,0],

φi(0)>0,i=1,2,3,4

(2)

(3)

由文献[12],系统(1)有满足初始条件(2)和(3)的唯一解(S(t),E(t),I(t),R(t))。容易得到系统(1)初始值定义在[0,+∞)的所有解，当t≥0时为正。

1 平衡点和局部稳定性

(R0-1)

(4)

Aβe-μτ(μ+δ)>(aA+μ)·

[δ(μ+ε)+μ(μ+γ+ε)]>

aA[δ(μ+ε)+μ(μ+γ+ε)]

即

βe-μτ(μ+δ)>a[δ(μ+ε)+μ(μ+γ+ε)]

因此, 当R0>1时, 正平衡点存在。系统(1)在无病平衡点处的特征方程为

(λ+μ)2[λ2+P1(τ)λ+P0(τ)+

(Q1(τ)λ+Q0(τ))e-λτ]=0

(5)

其中

P1(τ)=2μ+δ+γ+ε,

P0(τ)=(μ+δ)(μ+γ+ε)-δγ,

显然, 方程(5)有一个负实根λ=-μ, 其余的根由下面的方程来决定

λ2+P1(τ)λ+P0(τ)+
(Q1(τ)λ+Q0(τ))e-λτ=0

(6)

当τ=0, 方程(6)变为

λ2+(P1(0)+Q1(0))λ+P0(0)+Q0(0)=0

直接计算得到

P1(0)+Q1(0)=

[(μ+γ+ε)μ+δ(μ+ε)](1-R0)>0

因此，当τ=0时，无病平衡点E1是局部渐近稳定的。当τ>0时，设iw(w>0)是方程(5)的一个纯虚根,代入(5)式中，分离实部、虚部，直接计算得

w2-P0(τ)=Q0(τ)coswτ+Q1(τ)wsinwt,

P1(τ)w=Q0(τ)sinwτ+Q1(τ)wcoswτ

平方相加得

(7)

[(μ+δ)4+δ2(γ(2μ+2ε+γ)+

2δγ(μ+δ)2+2μδγ(μ+γ+ε)]>0

因此, 当R0<1时, 方程(7)无实根。注意到无病平衡点E1当τ=0时是局部渐近稳定的。由文献[13]的定理4.1, 当R0<1时, 无病平衡点E1是局部渐近稳定的。

记

f(λ)=λ2+P1(τ)λ+P0(τ)+

(Q1(τ)λ+Q0(τ))e-λτ

如果R0>1, 则

f(0)=(1-R0)[μ(μ+γ+ε)+δ(μ+ε)]<0

另一方面，当λ→+∞时，f(λ)→+∞，故方程(5) 至少有一个正实根,因此当R0>1时，无病平衡点E1不稳定。

下面考虑流行病平衡点E2的稳定性。系统(1)在流行病平衡点E2处的特征方程为

(λ+μ)[λ3+p2(τ)λ2+p1(τ)λ+p0+

(q2(τ)λ2+q1(τ)λ+q0)e-λτ]=0

(8)

这里

(2μ+δ+γ+ε)+α(μ+δ)·

q2(τ)=-α,

q1(τ)=-α(2μ+δ),

q0(τ)=-αμ(μ+δ)

方程(8) 有一个负实根λ=-μ, 其余的根由下面的方程决定

λ3+p2(τ)λ2+p1(τ)λ+p0+

(q2(τ)λ2+q1(τ)λ+q0)e-λτ=0

(9)

当τ=0, 方程(9)变为

λ3+(p2(0)+q2(0))λ2+(p1(0)+
q1(0))λ+p0(0)+q0(0)=0

当R0>1时，经过计算

并且

(p1(τ)+q1(τ))(p2(τ)+q2(τ))-(p0(τ)+q0(τ))=

(2μ+δ)[μ(2μ+δ+γ+ε)-μα]+

[(2μ+δ)(2μ+δ+γ+ε)-α(μ+δ)]·

其中

F2=(2μ+δ)[μ(2μ+δ+γ+ε)-μα]>0,

F3=[(2μ+δ)(2μ+δ+γ+ε)-α(μ+δ)]·

因此, 当R0>1时, 方程(9) 没有正实根, 平衡点E2当τ=0时是局部渐近稳定的。当τ>0时, 设iw(w>0)是方程(9)的一个纯虚根, 带入(9)中, 分离实部、虚部, 直接计算得

p1(τ)w-w3=

(q0(τ)-q2(τ)w2)sinwτ-q1(τ)wcoswτ

p2(τ)w2-p0(τ)=

(q0(τ)-q2(τ)w2)coswτ-q1(τ)wsinwτ

平方相加得到

w6+a4,0w4+a2,0w2+a0,0=0

其中，

因此若R0>1时, 方程(9)没有实根。注意到平衡点E2当τ=0时是局部渐近稳定的, 根据文献[13]定理4.1, 得到当R0>1时, 平衡点E2存在并且是局部渐近稳定的。有下面的结论。

定理1 对于系统(1)有,

(i)若R0<1无病平衡点E1是局部渐近稳定的；如果R0>1,E1是不稳定的。

(ii)若R0>1，系统(1)有唯一的流行病平衡点E2，并且它是局部渐近稳定的。

2 全局稳定性

通过构造合适的Lyapunov泛函并利用LaSalle不变集原理讨论系统(1)的无病平衡点E1和流行病平衡点E2的全局稳定性。注意到在E(t)系统(1)的第一、第三和第四个方程中并未出现, 因此只需要考虑系统(1)的子系统的稳定性

(10)

证明 记S0=A/μ,(S(t),I(t),R(t))是系统(10)具有初始条件(2)的解。定义

则V1(t)沿着系统(10)的全导数为

(11)

将A=μS0代入(11)式有

(12)

其中α如(4)式所定义。构造如下形式的Lyapunov 泛函

(13)

由(12)式和(13)式

(R0-1)I(t)

(14)

当R0<1时，由(14)式知V′(t)≤0。由文献[14]的定理5.3.1，定义M为集合{V′(t)=0}的最大不变子集。又由(14)式,{V′(t)=0}当且仅当S(t))=0,I(t)=0。注意到集合M是不变的, 对于集合M中的每个元素,有I(t)=0,I′(t)=0。因此由(10)的第二个方程,

0=I′(t)=δR(t)

证明 设(S(t),E(t),I(t),R(t)) 是系统(1)满足初始条件(2)-(3)的正解，由系统(1)的第二个方程和条件(3)得到

(15)

再由定理2, 当R0<1,t→∞时,

(16)

由(15)-(16)式，得

注意到当R0<1时, 系统(1)的无病平衡点E1是局部稳定的, 因此E1是全局渐近稳定的, 证毕。

下面为了证明系统(1)的正平衡点E2的全局稳定性, 首先来证明系统(10)的正平衡点E2的全局渐近稳定性。

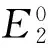
证明 设(S(t),I(t),R(t))是系统(10)具有初始条件(2)的正解, 定义

那么

另外，定义

构造如下形式的Lyapunov泛函

V2(t)=V2,0(t)+V2,1(t)

那么

函数

H(t)=1-f(t)+lnf(t)

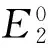
3 数值模拟

在本部分中, 对前面的相关的分析结果做数值模拟, 以验证这些结果。其中所采用的数据均是估算值。

例1 取参数值：A=0.9,μ=0.2,β=0.3,a=0.2,δ=0.2,γ=0.2,ε=0.2,τ=8, 此时经计算R0=0.286 906<1, 由推论1, 无病平衡点是全局渐近稳定的。如图1 所示。

图1 当R0<1时，系统(1)的无病平衡点E1是全局渐近稳定的Fig.1 The disease free- equilibrium E1is globally asymptotically stable whenR0<1

例2 取参数值：A=0.9,μ=0.2,β=0.3,a=0.2,δ=0.2,γ=0.2,ε=0.2,τ=0.6, 此时经计算R0=1.260 36>1, 由推论2, 无病平衡点是全局渐近稳定的。如图2 所示。

图2 当R0>1时，系统(1)的流行病平衡点E2是全局渐近稳定的Fig.2 The epidemic equilibrium E2is globally asymptotically stable whenR0>1

4 讨 论

在本文中,综合考虑了一类同时具有潜伏时滞, 复发因素的SEIR传染病模型,并完整地分析了模型的全局稳定性, 得到了疾病流行的基本再生数R0。如果R0<1,系统(1)的无病平衡点是全局渐近稳定的。相反,如果R0>1,流行病平衡点全局渐近稳定。由基本再生数的表达式容易得到,潜伏时滞越大,有效接触率越低, 基本再生数越小而且这种影响对于疾病的流行是指数级的。换言之,有效的控制疾病的潜伏期对于该类疾病的控制起着至关重要的作用，稍加延长疾病处在潜伏期内的时间就有可能大大减少疾病流行的可能性。

[1]FENGZ,HUANGW,CASTILLO-CHAVEZC.Ontheroleofvariablelatentperiodsinmathematicalmodelsfortuberculosis[J].JDynamDifferentialEquations, 2001, 13: 425-452.

[2]HUOH,FENGL.GlobalstabilityforanHIV/AIDSepidemicmodelwithdifferentlatentstagesandtreatment[J].ApplMathModel, 2013, 37:1480-1489.

[3]HETHCOTEHW,VANDENDRIESSCHEP.AnSISepidemicmodelwithvariablepopulationsizeandadelay[J].JMathBiol, 1995, 34:177-194.

[4]HETHCOTEHW,VANDENDRIESSCHEP.TwoSISepidemilogicmodelswithdelays[J].JMathBiol, 2000, 40: 3-26.

[5]GAOS,CHENL,TENGZ.PulsevaccinationofanSEIRepidemicmodelwithtimedelay[J].NonlinearAnal,RealWorldAppl, 2008, 9: 599-607.[6]VANDENDRIESSCHEP,ZOUX.Modelingrelapseininfectiousdiseases[J].MathBiosci, 2007, 207: 89-103.

[7]CHINJ.Controlofcommunicablediseasesmanual[M].Washington:AmericanPublicHealthAssociation, 1999.

[8]MARTINSW.Livestockdiseaseeradication:evaluationofthecooperativestate-federalbovinetuberculosiseradicationprogram[M].Washington:NationalAcademyPress, 1994.

[9]VANLANDINGHAMKE,MARSTELLERHB,ROSSGW,etal.Relapseofherpessimplexencephalitisafterconventionalacyclovirtherapy[J].JAMAJ,AmMedAsoc, 1988, 259: 1051-1053.

[10]ARDITIR,GINZBURGLR.Couplinginpredator-preydynamics:ratio-dependence[J].JTheorBiol, 1989, 139: 311-326.

[11]LID,MAW.AsymptoticpropertiesofanHIV-1infectionmodelwithtimedelay[J].JMathAnalAppl, 2007, 335: 683-691.

[12]COOKEK,VANDENDRIESSCHEP.AnalysisofanSEIRSepidemicmodelwithtwodelays[J].JMathBiol, 1996, 35: 240-260.

[13]KUANGY.Delaydifferentialequationswithapplicationsinpopulationdynamics[M].NewYork:AcademicPress, 1993.

[14]HALEJK,VERDUYNLUNELS.Introductiontofunctionaldifferentialequations[M].NewYork:Springer, 1993.

[15]HADDOCKJR,TERJEKIJ.Liapunov-Razumikhinfunctionsandaninvarianceprincipleforfunctional-differentialequations[J].JDifferEquations, 1983, 48: 95-122.

Long Time Behavior for an SEIR Epidemic Model with Latent Delay and Nonlinear Incidence Rate

YANGRuochen1,MAMingju2,QIYifei3,LIJun4

(1.Tobin College of Business, St.John’s University, New York NY11439, USA; 2. Department of Mathematics, Putian University, Putian 351100, China; 3. School of Economics, Northwest Normal University, Lanzhou 730070, China; 4..School of Mathematics and Statistics, Xidian University, Xi’an 710071, China)

A mathematical model describing the transmission dynamics of disease with nonlinear incidence rate and delay is constructed. The local stability of the disease-free equilibrium and epidemic equilibrium is established by analyzing the corresponding characteristic equation. Using suitable Lyapunov function and LaSalle’s invariance principle, it is proved that ifR0≤1thenthedisease-freeequilibriumisgloballyasymptoticallystable,butifR0>1thentheepidemicequilibriumisgloballyasymptoticallystable.Somenumericalsimulationsarealsogiventoexplaintheconclusions.

epidemic disease; mathematical model; incubation period; latent relapse; delay; global stability

2014-07-31

福建省教育厅中青年教师教育科研资助项目(JA13283)

杨若晨(1994年生), 男；研究方向：微分方程与动力系统；通讯作者：李君；E-mail:j.lee.nx@gmail.com

10.1347/j.cnki.acta.snus.2015.01.006

O

A

0529-6579(2015)01-0024-07