巧抓问题设计 力促“真学课堂”

罗世树

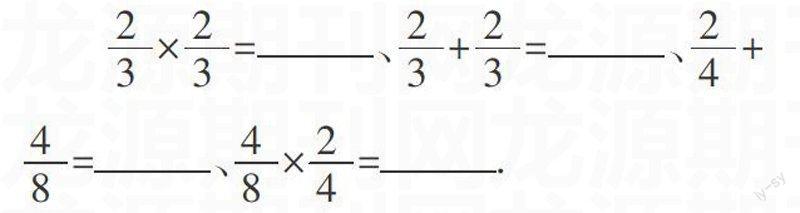
【关键词】问题设计 真学课堂

小学数学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2015）05A-

0073-01

在“真学课堂”中，所有的课堂教学设计都服务于学生的学习，其中也包括课堂问题的设计。教师应先把握好设计课堂问题的分寸，实现有效启发，再设计目标明确的问题，实现学生主动参与教学活动，最后要设计框架完整的问题，实现课堂知识的高效迁移，拓宽学生的思维路径。本文笔者将结合自身的教学经验，从三个方面来谈谈如何巧妙地做好问题设计，从而有效地促进“真学课堂”。

一、设计要有分寸，重在实现有效启发

在“真学课堂”的基本要求中，明确提出小学数学课堂要“注重启发，彰显自主”。因此，课堂问题的设计要把握好问题的分寸，重在实现有效启发。具体来说，把握好问题的分寸就是要有深度，能“开启”学生的思维。但深度并不代表难度，教师在设计问题时不但要熟知课本内容结构，还要对学生的数学技能掌握程度和知识水平有全面的了解。另外，分寸合理的问题是具有发展性的，难易不一，不能要求所有学生都能解答，难度较大的让优等生回答，中等难度问题由一般学生回答，容易的问题让成绩不太好的学生来思考回答，让他们在思考中提升知识水平。

例如，在教学人教版五年级上册《三角形的面积》时，教师可以先根据教学重难点设计好问题，然后让后进生回答概念性或导入性的问题：“平行四边形面积计算的公式是什么？”让中等生回答连接新旧知识的“跳板”问题：“三角形可以转变成什么图形？怎样才能把三角形变成平行四边形？”最后让优等生回答较困难的推导性问题：“平行四边形面积计算与三角形面积计算之间是否存在一定的联系？已知平行四边形的面积，我们是否可以推导出三角形面积计算的有关公式呢？”这样一来，课堂问题的分寸就能得到较好地把握，三个层面学生的数学思维都能得到启发，促进了“真学课堂”的形成。

二、设计要有目标，重在实现主动参与

“真学课堂”要求学生能以饱满的热情参与到学习过程中。因此，课堂问题的设计要有明确的目标，实现让学生主动参与课堂活动。要达到这个要求，教师不是指直接抛出一个课题让学生们自主研究，这不符合小学生的学习心理特点，而是指设计的问题要有具体目标，情境要贴合实际，难度指数要符合学生的能力水平。这样才能激发学生主动质疑，培养学生主动参与的意识。

例如，在教学人教版五年级数学下册《长方体和正方体》时，小学生对于空间立体图形的想象力较差，需要教师深入讲解，帮助学生掌握立体图形。为了调动学生参与到思考中，教师在讲解完基本概念后，明确立体图形是由多个相互交叉的面组合而成的，接着设置一个问题情境：在一个巨大的长方体木箱的一个角落，有一只蚂蚁在觅食，它通过嗅觉发现了箱子另一端的顶点上有食物，那么蚂蚁该怎么爬过去才能最快找到食物呢？蚂蚁是学生熟悉的昆虫，这个问题一下子吸引了学生的注意力，他们纷纷开始讨论。学生最终能否回答出来不重要，重要的是学生在思考这个问题的过程中，已经在脑海里形成了一个立体图形，锻炼了学生的空间想象能力，达到了调动学生积极性的目的，实现“真学课堂”。

三、设计要有框架，重在实现高效迁移

“加强联系，迁移应用”是“真学课堂”提出的另一个要求，要求加强不同知识点的联系教学，达到学生能迁移应用知识的目的。所以，课堂问题的设计要有框架，重在实现知识的高效迁移。有框架的课堂问题能给学生带来一个完整的知识架构，实现在同一框架内不同知识点的有效联系。设计有框架的问题一般要符合几个特点：存在新知与旧知之间的联系、学生有能力进行比较与辨认、能实现知识的迁移。学生在读题解题时尝试审视问题序列，发掘知识联系，自行探索发现规律，形成属于自己的知识网络，实现知识迁移。

例如，在教学人教版六年级数学上册《分数乘法》时，在讲授了分数乘法的基本原则后，为了实现分数加减和分数乘法知识的相互迁移应用，提高对分数乘法的认识，教师可以设置如下几道题目：

■×■=■、■+■=■、■+■=■、■×■=■.

学生通过训练，在分数运算法则的框架内，学会复习分数加法的运算规则，同时又会和刚学的分数乘法对比，发现分数加法和分数乘法之间的区别与联系：“分数加法分母必须一样才能运算，而乘法就不必，可以直接运算。”这样就实现了分数不同运算法则的知识迁移，形成“真学课堂”。

总之，只有摒弃以往“模式化”的问题设计，把摸索和思考的空间交给学生自己完成，让问题成为引导他们成长的指路棒，这样的课堂才是学生成长的磨炼场，智慧的增长源，能力的晋升地。

（责编 林 剑）