新疆少数民族数学文化情景教学素材开发研究

刘 超 马倩倩

（石河子大学师范学院，新疆 石河子832000）

一、新疆少数民族数学文化情景教学素材开发思路

新课改已进行10年有余，随着课改的不断深入，课堂教学也逐渐地因课改而精彩起来，通过数学教学提升学生数学素养、促进其全面发展的理念也逐渐清晰可见，中小学一线名师的课堂教学给我们带来了崭新的视觉享受。各版本教材也为适应课改变化，进行了全方位、大幅度地修订。人教版中学《数学》教材主编林群院士指出:希望教师们树立“以人为本”的教育思想，鼓励学生通过生动活泼、积极主动的学习，在培养更广泛的数学学习兴趣、不断增强用数学的意识和能力的同时，接受数学文化的熏陶，不断提升数学文化素养，促进人格品质的良好发展，更全面地发挥数学在科学教育与人文教育方面的功能。［1］

在新疆少数民族地区，课改的影响力也能从教师的教学行为、教学模式变化等方面发现，但与林群院士所提出的数学素养和能力目标还相去甚远。当前，新疆少数民族地区数学教育教学存在诸多问题。如教师学科专业知识和教育教学知识不足（南疆还普遍存在非数学专业教师从事数学教学），教师课程资源开发与应用能力不高等。新疆大部分地区目前选用的是人教版数学教材，非双语班的学生使用的是由汉语翻译成维吾尔语或哈萨克语或其他语言版的教材。不可否认的是，现行教材情境“城市化”倾向明显，如人教版教材里出现了“摩天轮、商场打折，甚至纳米、“神五”等实际例子，新疆的一些少数民族孩子对这些事物没有任何概念。教材中涉及的这些情景素材远离了少数民族地区生产生活实际，远离了少数民族学生的日常生活经验，教学中存在困难，甚至出现负面影响也是在所难免的。林群院士曾指出:应从学生的终身发展需要出发，不拘泥于教材中的内容，努力开发着眼于促进学生数学素养全面提升的学习素材。跨文化数学教育研究结论也表明:不同的经济环境和文化背景直接影响着不同地区不同民族青少年数学能力的发展，而直接影响数学教育的文化因素主要有数学文化、民族语言、传统观念、家庭环境、教育状况。［2］我们坚持认为，弥补当前国家统编数学教科书对于少数民族传统文化“缺失”或者“不足”之处，积极开发顺应少数民族儿童社会生活实际以及认知规律的、蕴含少数民族地区的民风民俗、风土人情、文化环境和教育观念的、着重凸显数学知识在少数民族人民社会生活中实际应用的数学课程资源或教材建设是推动少数民族地区数学教育发展的一项重要任务。

正是基于以上认识，我们开始了针对新疆少数民族传统文化的数学课程资源的研发工作。前期的田野调查、访谈以及文献阅读都表明，新疆少数民族数学课程资源开发利用的载体包括物质文化和非物质文化形式两大类，其中物质文化载体涉及新疆各少数民族特色饮食、民族传统服饰、刺绣工艺、地毯工艺、建筑装饰艺术等多个方面。这些凝结在实物上的潜在的数学文化内容只有通过分析、挖掘或抽象才能用文字语言、数学术语或几何图形重新概括表达出来。数学课程资源的非物质文化载体涉及新疆各少数民族人民在本民族社会历史实践过程中所创造的各种精神文化（涉及语言、文字、文学、科学、艺术、哲学、宗教、风俗、节日、传统等方面）方面使用的数学知识。此外，我们还可以从民间故事、民俗、民间美术、表演艺术、传统手工艺技能等多个方面提炼出情境教学素材。

在厘清少数民族数学课程资源载体形式的基础上，接下来就要通过文献、古籍以及史志检索、田野调查、访谈等搜集整理涉及数学知识应用的文化载体，并从数学的视角从中提炼出应用的数学知识，并加以整理、分析和细化。在整理少数民族传统数学文化的基础上，还要结合现行课程标准、现行国家统编教材、民族儿童认知规律等方面实现这些素材的教育学转化，开发应用于民族地区数学教育的不同形式的课程资源或教材建设（整个研发过程如图1所示）。

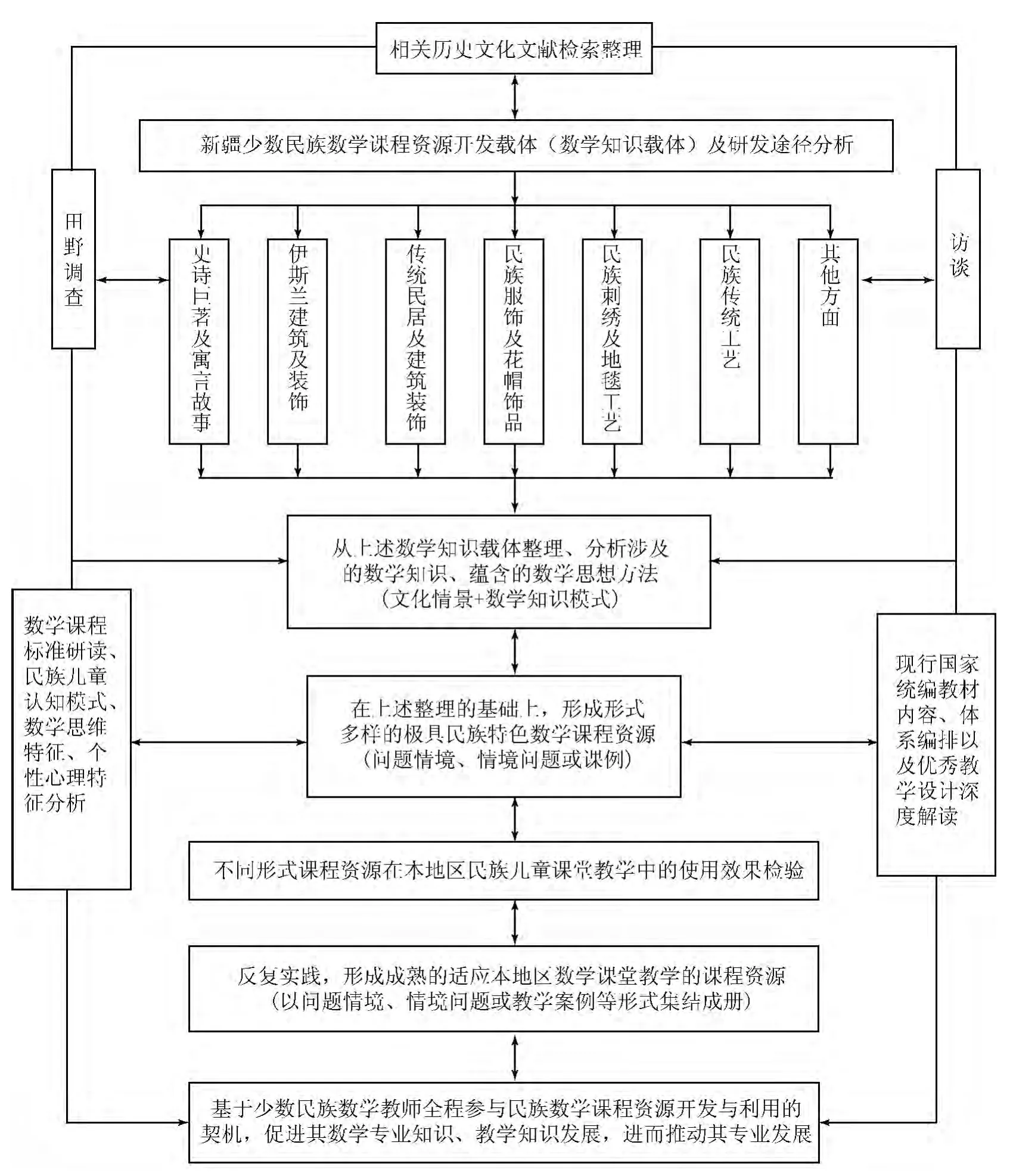
图1 新疆少数民族数学文化课程资源开发模式

二、新疆少数民族数学文化情景教学素材开发实践

1.代数方面

有关代数方面的情景素材主要是将包含新疆少数民族风土人情、民族风俗以及日常生活事物等作为情景来编制数学问题应用于课堂教学。

情景问题1:骆驼是被称为“沙漠之舟”的哺乳动物（如图2所示）。骆驼行走的速度是14.5～16 km/h。假如一只骆驼日夜不停地奔走，请问2天能行走多远？

情景问题2:新疆毛肉兼用细毛羊，简称新疆细毛羊（如图3所示）。

（1）一片牧场长满牧草，牧草均匀生长，这片牧草可供10只新疆细毛羊吃20天，可供15只细毛羊吃10天，问:如果是25只细毛羊可吃多少天？

（2）牧场原有库存饲料一定，而且每天都买进相等数量的饲料入库，5只羊连续吃20天可吃完，6只羊连续吃15天可吃完，若要求6天正好全部吃完，至少需要多少只羊？

情景问题3:世界最大的温度计位于新疆吐鲁番火焰山景区内（如图4所示），在火焰山风景区的地宫中心，高高伫立着一根巨大的温度计，这根落成于2004年8月16日的立体造型温度计，名叫“金箍棒”，曾获“大世界吉尼斯之最”。已知巨型温度计直径0.65m。

（1）从巨型温度计离地5m处向地面拉一条缆绳，这条缆绳在地面的固定点距离温度计底部12m，同样用这条缆绳从温度计的顶端拉到地面，固定点距温度计底端5m，请问巨型温度计有多高？

（2）试求巨型温度计的体积是多少？

图2 骆驼

图3 新疆细毛羊

图4 “金箍棒”温度计

2.几何方面

有关新疆少数民族传统文化几何方面的情境素材主要是应用在新疆各少数民族传统服饰、建筑图案及装饰工艺、日常生活的其他方面所使用的几何纹饰，这些几何纹饰表达了人们对美的追求。从这些几何纹饰可以发现，许多方面都是以几何学为基础。

情景问题4:新疆手鼓又称达卜，因敲击时发出“达”、“卜”两种音响而得名。手鼓是新疆各族人民庆祝丰收、节日的常用乐器。图5为很多不同型号的手鼓放到一个最大型号的手鼓里，把它抽象成图6所示图形，已知大圆O的半径为0.6m，根据图6回答以下问题:

图5 手鼓

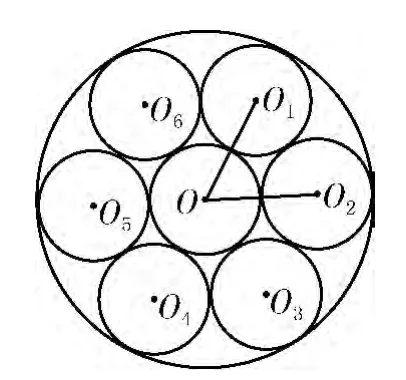
图6 手鼓几何图

（1）大圆O和小圆O有什么位置关系？

（2）大圆O 和圆O1，O2，O3，O4，O5，O6的位置关系是什么？

（3）小圆O和其他小圆有什么关系？

（4）求∠O1OO2的角度。

（5）求小圆O的半径和面积。

（6）分别求出大圆O与小圆O的半径、直径、面积比，并分析半径比、直径比以及面积比之间的关系。

情景问题5:皮山县隶属和田地区，图7为皮山县古代民间屋顶图案，屋顶造型简洁，具有明显的几何特征。图8是图7的几何图形。如图8，圆O是正六边形ABCDEF内接圆，已知正六边形ABCDEF边长为5cm，根据图8回答下列问题:

（1）圆O的半径是多少？圆O的面积是多少？

（2）若正六边形ABCDEF与正六边形A′B′C′E′F′的边长比为3∶5，请问面积比是多少？写出详细过程。

（3）图8是轴对称图形吗？如果是，请画出对称轴；如果不是，请说明理由。

（4）以点O为直角坐标系原点建立直角坐标系，求出点D和E′的坐标值。

图7 古代民屋顶图案

图8 古代民屋顶图案几何图

情景问题6:新疆的房屋千姿百态，或款式不同，或装饰部位不同，或图案和工艺不同。房屋注重审美，朴素与华贵相得益彰，展示出人们的聪慧和高超技艺，是民族文化之瑰宝。

图9是建筑的窗户局部图案，图10是图9其中一个图案的放大图，这些图案造型简洁，色彩明快，具有明显的几何特征。图11是图9窗户内部花纹的几何图形。在图11的正六边形A1B1C1D1E1F1中，

图9 窗户局部图案

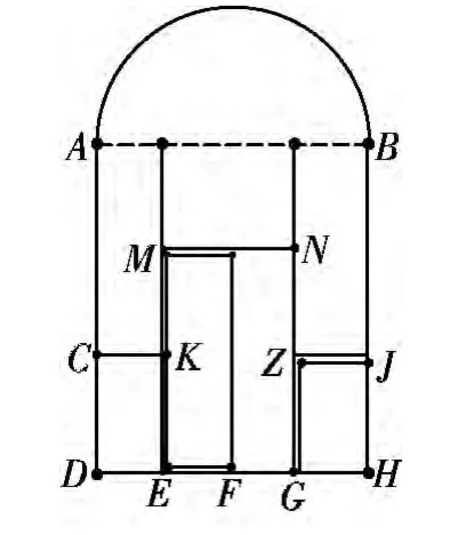
图10 窗户局部图案放大图

图11 窗户内部花纹的几何图

点A2，B2，C2，D2，E2，F2是线段A1O，B1O，C1O，D1O，E1O，F1O 的中点。在图10中E，F，G 是线段DH的四等分点，C，J分别是线段AD，BH 的三等分点。K，Z分别是线段ME，NG的中点。请回答下列问题:

（1）如果三条直径将六边形分为6等份，那么每个三角形是什么样的三角形？

（2）如图10窗户平面图中有哪些平面图形？可分为几个区域？

（3）图10中有哪些面积相等的平面图形？

（4）图11中若A1B1＝4m，则内部小正六边形A2B2C2D2E2F2的周长为多少？

如上呈现的是我们开发的部分情景教学案例，笔者认为，开发少数民族数学情景教学素材及课程资源的最终目的是实现本地区数学课堂的有效教学、数学教育质量的提高以及儿童数学素养的提升。但我们也应认识到，基于少数民族传统文化的数学课程资源与主流数学（课本上的数学）相比，仍然有一定的局限性。因此，在开发与使用课程资源的过程中还必须考虑其与主流数学的关联，尽可能地从数学的精神、思想和方法上实现两者的共通。

［1］课程教材研究所.教师培训手册（数学:七—九年级）［M］.北京:人民教育出版社，2014:23－26.

［2］罗永超，吕传汉.民族数学文化引入高校数学课堂的实践与探索——以苗族侗族数学文化为例［J］.数学教育学报，2014，23（1）:70－74.