小学生个性化特征对学习资源选择的影响研究
2015-06-12胡灵敏吴敏华骆力明
胡灵敏 吴敏华 骆力明
(首都师范大学信息工程学院,北京100048)
泛在学习环境下,学习者学习方式的改变促进着教材形式的变革。数字教材作为推行教学改革、提升教学质量的关键环节,越来越得到人们的重视。[1]在这种新的学习环境下,数字教材不仅要为学习者提供丰富的学习资源,而且要满足学习者的不同需求,即实现个性化学习。但是,由于学习资源数量和种类繁多,学习者对各类学习资源的需求亦是层出不穷,如何实现学习资源对学习者的个性化推送成为众多教育研究者的研究话题。[2]
多数国内外研究者在对学生进行个性化资源推送时,主要将学习风格、认知风格作为个性化资源推荐的依据,推断出其可能感兴趣的学习资源类型和内容,进而进行算法和系统的设计,以满足向学习者个性化推荐学习资源的需求。[3-7]但是除学习风格、认知风格外,对于学习者的其他个性化特征与个性化资源之间关系的研究并不多见。笔者通过对一线教师和专家的访谈,了解到学生的学习兴趣、学习过程、网络自我效能感对学生的资源选择偏好会产生一定的影响。鉴于此,本文以小学英语学习资源为例,从学习者的英语学习兴趣、学习过程、网络自我效能感三个方面分析影响学习者选择不同类型学习资源的因素,采用层次分析法来确定了学习兴趣、学习过程、网络自我效能感对于学生选择不同类型学习资源的影响权重,并以视频有字幕与视频无字幕两种资源为例验证所建立的指标体系的有效性,以期为今后个性化资源推荐系统的研究和算法的设计提供一定的理论支持。
一、资源选择指标体系的建立
1.层次分析法
层次分析法(Analytic Hierarchy Process,AHP)是20世纪70年代由美国著名运筹学家T.L.Satty提出的,该方法可以将经验认知与理性分析相互结合,利用思维过程的数量化大大降低主观因素对结论的影响,因而在权重运算中获得广泛的应用。[8]由于AHP同样适合于评价结构复杂、难以量化的对象[9],作为一种定性与定量相结合的决策分析方法,它的整个决策过程可以充分反映决策者对决策问题的认识。层次分析法采用梯级决策方式,将复杂问题分解成若干层次和因素,并将各因素进行比较,进而计算各因素对决策问题的权值,为最佳方案的选择提供依据。[10]为更准确地确定学习者的个性化特征对于学生的影响程度,本次研究选用层次分析法作为主要的数据分析方法。
2.指标体系的构建
(1)一级准则层的确定。在此次研究中,小学英语个性化资源的选择将作为层次分析模型的最终目标,将学习兴趣、学习过程、网络自我效能感作为准则层的一级指标。
(2)二级准则层的确定。对于学习兴趣,我们根据周明星、邓新华的英语学科学习兴趣量表,并对量表题目进行归类分析,将学习兴趣分为两个维度——文字兴趣与视听说兴趣。为了更精确地描述学生在学习过程中的状态,我们根据Kember的学习过程分类方法及学习过程量表的结构,将学习过程分为深度学习和浅层学习两个部分。[11]Ying-Tien Wu等将学生的网络自我效能感分为一般自我效能和交流自我效能两个子因素。[12]因此,本文将一般自我效能和交流自我效能作为网络自我效能感的下一级指标。
根据以上分析,建立学生学习资源选择指标体系(如图1所示)。

图1 学生学习资源选择偏好指标体系
二、指标权重系数的确定
1.判断矩阵的确定
在层次分析模型中,判断矩阵是根据模型中同一层次的元素关于上层元素的重要程度建立的,同一层元素两两比较的结果构成判断矩阵A=[aij],其中aij代表本层指标中指标i相对于指标j的重要程度。1970年美国运筹学家萨蒂(Saaty)提出的1~9标度法[13],是目前在建立判断矩阵时运用较为广泛的相对客观的主观赋权法。本文同样采用此方法来对元素间的重要性程度进行标注(如表1所示)。

表1 1~9标度法
本文主要采用专家调查法来确定其各因素之间的相对重要程度。将专家调查的结果汇总,一级准则层各因素相对重要程度结果如表2所示。

表2 一级准则层各因素的相对重要程度
二级准则层各因素相对重要程度结果如表3所示。

表3 二级准则层各因素的相对重要程度
根据表2和表3分别构造出各层次指标两两比较的判断矩阵,所有判断矩阵如下:

2.层次单排序及一致性检验
层次单排序是指每个判断矩阵各因素针对上层指标的相对权重,本质上是计算权向量。利用线性代数的知识,计算层次分析模型中各判断矩阵的最大特征值及其对应的特征向量,并将特征向量标准化(归一化),所得的向量即为该判断矩阵对应的权向量。[14]计算判断矩阵的特征向量与最大特征值的方法有幂法、和积法、方根法等等,本次研究采用方根法计算特征向量和最大特征值[15],步骤如下:
(1)计算判断矩阵每行元素的乘积

(2)计算乘积的m方根

(3)将权向量归一化

W=(w1,w2,…,wm)即为所求特征向量,向量中的各数值即为其对应指标的权重。
(4)计算判断矩阵的最大特征值
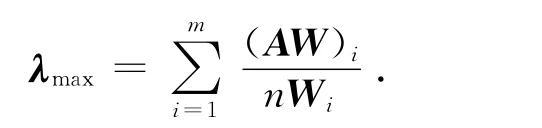
在指标体系复杂度较高的情况下,有时两两比较可能会出现不一致的情况,因此对于建立的判断矩阵需要进行一致性检验。一致性程度使用随机一致性比率CR=CI/RI来表示,其中λmax为矩阵的最大特征值,RI由随机一致性指标来表示(如表4所示)。m为判断矩阵维数。当CR<0.1时表示矩阵具有满意的一致性,即判断矩阵通过了一致性检验,否则需要对判断矩阵重新调整。

表4 随机一致性指标
对所有判断矩阵进行层次单排序和一致性检验,最终结果如表5所示。

表5 层次单排序及一致性检验
进而计算得各指标的具体权重值如表6所示。

表6 各指标的具体权重值
由此我们可以看出,二级准则层各因素对学生资源选择的影响程度从大到小依次为深度学习、视听说兴趣、交流自我效能、文字兴趣、浅层学习、一般自我效能。
三、有效性验证
本次研究通过设计资源选择实验并将学生的资源选择结果与层次分析结果进行对比来分析所建立的资源选择指标体系的有效性。
1.层次分析法资源选择方案
根据小学生的年龄特点,视频类型的资源对其更具有吸引力,故此,本文选用视频有字幕(标记为A)与视频无字幕(标记为B)两种资源作为验证资源选择指标体系的资源方案(如图2所示)。

图2 学生学习资源选择偏好模型
(1)方案层层次单排序及一致性检验。方案层各类资源相对重要程度的专家调查结果如表7所示。

表7 方案层各类型资源的相对重要程度
根据一级准则层判断矩阵建立方法和表7的数据,建立方案层判断矩阵如下:

方案层各资源的层次单排序结果如表8所示。

表8 层次单排序结果及一致性检验
(2)层次总排序。总排序是指每一个判断矩阵各因素针对目标层的相对权重。这一权重的计算采用从上而下的方法,逐层合成。假设第k层n个元素对于上一层(第k层)第j个元素的单排序权重是,其中不受j支配的元素的权重为零,表示第k层元素对第k-1层元素的排序。若第k层元素对于总目标的总排序为[16]
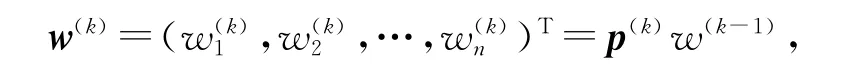
则

同样,也需要对总排序结果进行一致性检验。
根据资源选择指标体系及方案层层次单排序结果,对整体层次分析模型进行层次总排序,最终确定最佳资源选择方案,结果如表9所示。

表9 层次总排序结果及一致性检验
由此可以看出,相对于视频无字幕的学习资源来说,学生更容易选择视频有字幕类型的资源来进行学习。
2.学生学习资源选择实验
本文对北京市某小学五年级3个班的学生进行了资源选择实验。在实验过程中3个班各有2名实验者进行监督,保证实验的正常进行。资源选择实验在学生机房进行,学生每人一台电脑,每台电脑上都存放着由一线教师和相关教育专家经过多次调查与筛选所得的学习资源,其中资源类型分为视频有字幕、视频无字幕两种,每种类型5个资源,各类型资源难度与相关课程标准要求相当,资源内容与五年学生学习水平相当。学生按照要求依次查看学习资源,选择2个自己最喜欢的资源并记录在研究人员事先准备好的空白打印纸上,最后由研究人员将学生选择的资源情况录入Excle表格进行统计分析。统计后得出全体学生共选择了211个资源,其中视频有字幕120个,视频无字幕91个(两种资源选择比例如表10所示)。

表10 学生学习资源选择情况
将表9与表10进行对比可以看出,根据指标体系计算所得的资源选择情况与学生实际选择情况基本一致,所建立指标体系能够为学生的资源选择提供一定的参考依据。
四、结论
由以上分析我们可以看出,在学习兴趣、学习过程、网络自我效能感三个学生个性化特征中,学习过程对学生资源选择的影响程度最大,学习兴趣次之,网络自我效能感最后。指标体系的二级准则层各因素对学生的资源选择的影响程度从大到小依次为深度学习、视听说兴趣、交流自我效能、文字兴趣、浅层学习和一般自我效能。
根据资源选择指标体系及其权重系数,并结合资源选择模型,我们可以推算出某个学生的资源选择偏好。
W={0.103 6,0.207 2,0.411 2,0.082 2,0.065 3,0.130 5},表示资源选择模型中二级指标层权重向量。
F={U11,U12,U21,U22,U31,U32},表示学生具有二级指标层各项特征的程度向量。
以视频有字幕与视频无字幕两种类型的资源为例,将表8数据转换成学生个性化特征——资源矩阵(R)

则不同的学生对于两种学习资源的偏好程度可以用下式表示:
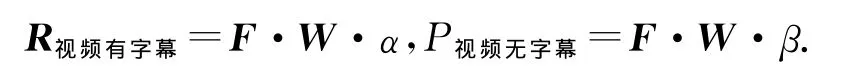
本文根据课堂观察及对教师的访谈情况,主要针对学习兴趣、学习过程、网络自我效能感对学生资源选择的影响进行了分析,并以某小学5年级学生作为研究样本,分析了学习兴趣、学习过程、网络自我效能感及其子因素对于学生资源选择的影响情况,建立了基于学生个性化特征的学习资源选择指标体系,确定了各因素对学生学习资源选择的权重,最后通过学生资源选择实验进行了指标体系的验证,为当前学习资源个性化推荐系统的算法设计提供一定的理论支撑。在未来的研究中将会对本次研究所建立的指标体系进行进一步的完善,并在此基础上进行个性化资源推荐算法的设计。
[1]胡畔,王冬青,许俊,韩后.数字教材的形态特征与功能模型[J].现代远程教育研究,2014(2):93-99.
[2]杨丽娜,肖克曦,刘淑霞.面向泛在学习环境的个性化资源服务框架[J].中国电化教育,2012(7):84-88.
[3]陈敏,余胜泉,杨现民,黄昆.泛在学习的内容个性化推荐模型设计[J].现代教育技术,2011,21(6):13-18.
[4]Karampiperis P,Sampson D.Adaptive Learning Resources Sequencing in Educational Hypermedia Systems.Educational Technology & Society,2005,8(4):128-147.
[5]Yang T C,Hwang G J,Yang S J H.Development of an Adaptive Learning System with Multiple Perspectives Based on Students'Learning Styles and Cognitive Styles[J].Educational Technology & Society,2013,16(4):185-200.
[6]刘建国.教学资源个性化服务模型及其实现技术研究[D].重庆:西南师范大学,2004.
[7]孙众,骆力明,綦欣.数字教材中个性化学习资源的推送策略与技术实现[J].电化教育研究,2014(9):64-70.
[8]Saaty T L.Decision-making for leaders:The Analytical Hierarchy Process for Decisions in a Complex World[J].Pittsburgh,PA:RWS Publications,1995.
[9]周蓉.高校教师远程教学胜任力评估体系构建[J].电化教育研究,2014(4):112-120.
[10]王元放,俞晓安,薛阳,敬忠良,周宏仁.基于层次分析法的信息化项目评估模型[J].计算机工程,2007,33(8):68-70.
[11]Kember D,Biggs J,Leung D Y P.Examining the Multidimensionality of Approaches to Learning Through the Development of a Revised Version of the Learning Process Questionnaire[J].British Journal of Educational Psychology,2004,74(2):261-280.
[12]Wu Y T,Tsai C C.University Students'Internet Attitudes and Internet Self-efficacy:a Study at Three Universities in Taiwan[J].CyberPsycholgy & Behavior,2006(9):441-450.
[13]Saaty T L.The Analytic Hierarchy Process[M].New York:McGraw-Hill,1980.
[14]道客巴巴.层次分析法实例[EB/OL].[2014-09-02].http://www.doc88.com/p-271833857833.html.
[15]黄倩,王蔚.层次分析法在电子游戏教育性评价中的应用研究[J].中国远程教育,2010(10):18-21.
[16]百度文库.层次分析法步骤[EB/OL].[2014-09-02].http://wenku.baidu.com/view/95fc165077232f60ddcca192.html.
