且探且反思
——含参绝对值二次函数解法的教学思考
2015-06-12江口中学浙江奉化315504
●江 杨 (江口中学 浙江奉化 315504)
且探且反思
——含参绝对值二次函数解法的教学思考
●江 杨 (江口中学 浙江奉化 315504)
二次函数一直是高中数学的重要内容,通过二次函数可以研究函数的许多性质(单调性、奇偶性、最值等)以及“3个二次”的综合运用等问题.其中含参数绝对值的二次函数,由于涉及数学思想方法多、综合性强、分析能力要求高等特点,在高考中也常有体现.随着浙江省数学高考“导数退位,函数扶正”,含参绝对值二次函数的题型很可能涉及.下面笔者结合一堂教学课,也谈解法,更贵反思,望同行批评指正.
1 题目呈现
例1 已知函数f(x)=x2-2x|x-a|,a∈R在区间[0,2]上的最小值为-1,则a=______.
例2 设集合A={x|x2-|x+a|+2a<0,a∈R},B={x|x<2},若A≠φ且A⊆B,则实数a的取值范围是______.
(2014年浙江省杭州市第2次高考质量检测试题)
2 学生思维寻迹
例1是一道期中考试的填空题,从学生考后的情况来看,大部分是“逃”和“猜”2种对策,少部分有思路但也答而不全,答对的更寥寥无几.因此,联系到2015年的数学高考实际,笔者就含参绝对值二次函数这一内容设计了一堂专题课.课堂上,笔者先让学生“还原”了他们的思维过程:
师:这个函数在区间[0,2]上的单调性确定吗?不确定怎么能直接代入呢?
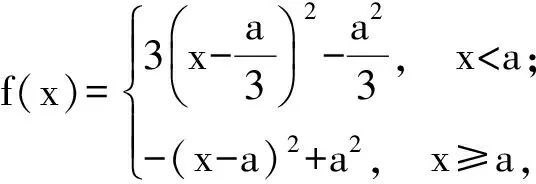
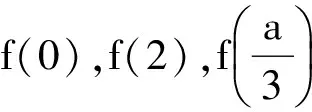
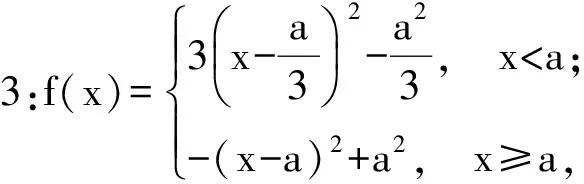
当a≤0时,f(x)在x∈(0,2)上为单调递减函数,从而
f(x)min=f(2)=-(2-a)2+a2=-1,
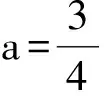
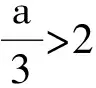
f(x)min=f(2)=-(2-a)2+a2=-1,
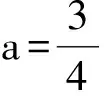
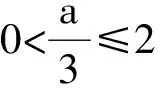
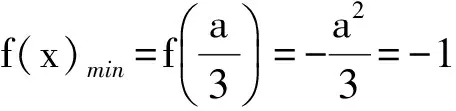
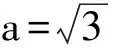
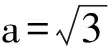
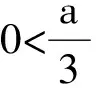

当a≤0时,f(x)在x∈(0,2)上为单调递减函数,从而
f(x)min=f(2)=-(2-a)2+a2=-1,
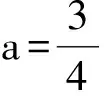
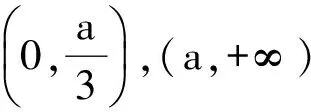
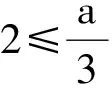
f(x)min=f(2)=-(2-a)2+a2=-1,
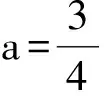
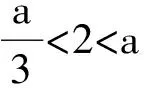
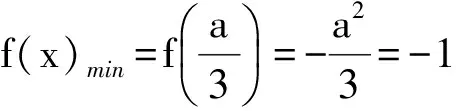
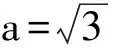
3)当a≤2时,
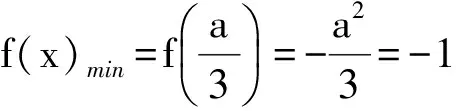
或
f(x)min=f(2)=-1,
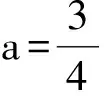
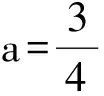
本题笔者仅就解法探讨在此提供另外一种方法——导数法.

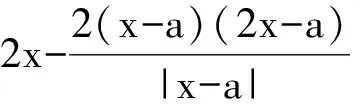
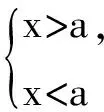
当a≤0时,f(x)在R上为单调递减函数,从而
f(x)min=f(2)=-(2-a)2+a2=-1,
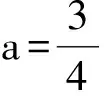
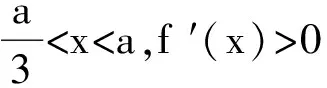
若问题仅仅止步于此,那还只是浅尝辄止,未及该类问题全部.笔者认为合格的数学教师应该有由点及面的推广总结能力、拨云见日的剖析归类能力,例2便是例1的推广归纳(教师引导,学生自主完成).
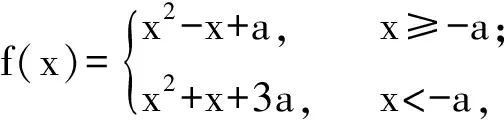
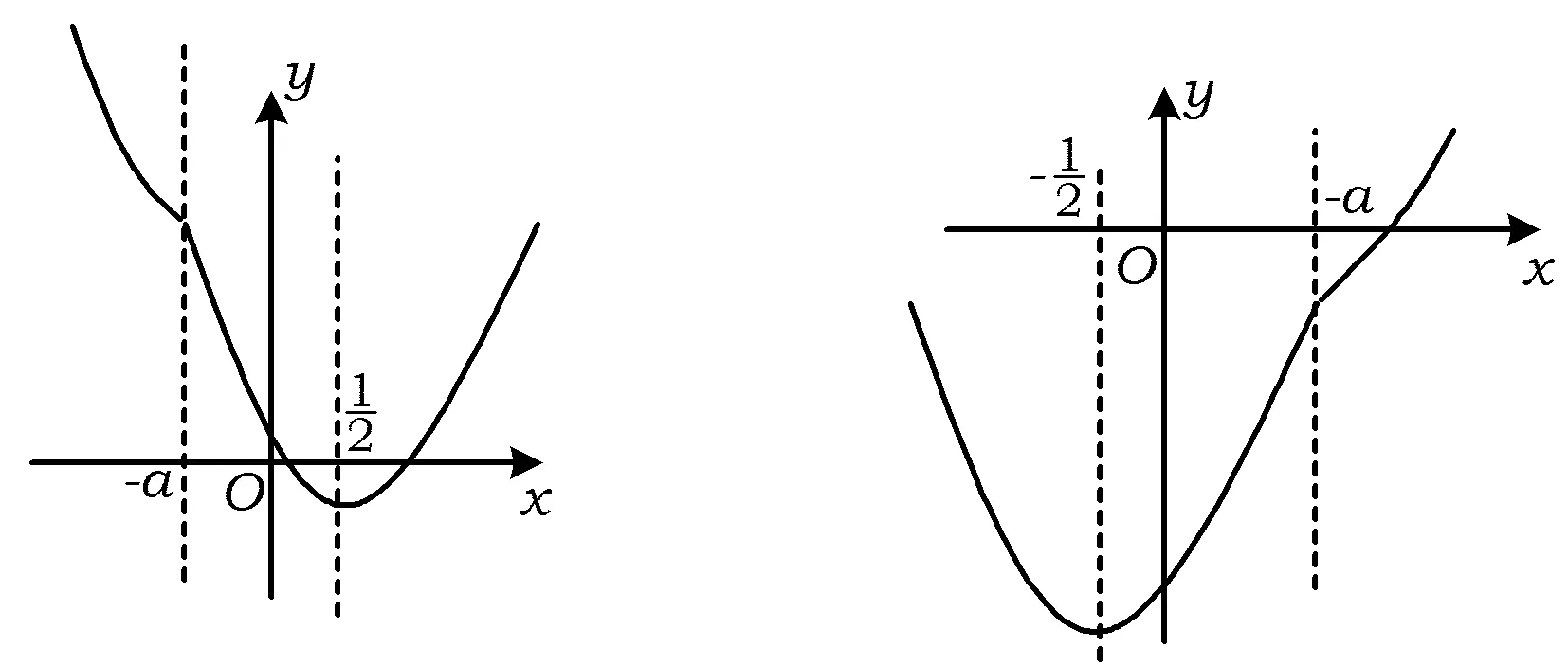
图1 图2
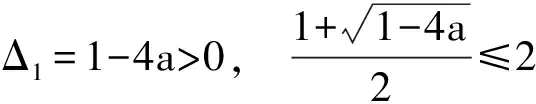
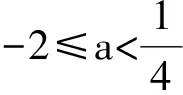
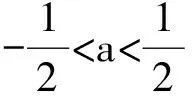

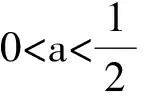
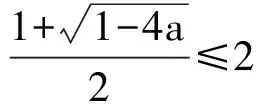
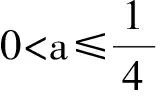
1.3 统计学方法 采用SPSS 19.0统计学软件对数据进行分析。计量资料用均数±标准差表示,组间比较采用t检验。在分析过程中,多组间的数据比较处理采用One-way ANOVA方法进行分析。以P<0.05为差异有统计学意义。
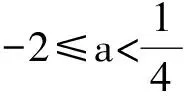
3 推广归纳类型,总结提炼方法
例1可推广归纳为“f(x)=bx|x+a|+g(x)(其中g(x)至多为二次函数,a,b之一为参数)”型.
此类函数的绝对值涉及二次项,若b为参数,a为常数,转为分段函数后图像开口确定需结合b的值进行讨论;若a为参数,b为常数,则先由分界点-a去掉绝对值,当g(x)为一次函数时,f(x)的图像由开口向上和向下的2段抛物线拼接成,分类讨论a,再结合区间分析,当g(x)为二次函数时,图像不同,方法相同.
例2可推广归纳为“f(x)=b|x+a|+g(x)(其中g(x)为二次函数,参数为a,b中之一)”型.
此类函数的绝对值涉及一次项,无论参数为a或b,开口确定,转为分段函数后,若b为参数,对称轴需结合b的值进行讨论,若a为参数,对称轴确定,图像需按分界点-a讨论.
以上涵盖了含参绝对值二次函数的一般类型.笔者再列举几道高考试题作为巩固.
1.设a为实数,函数f(x)=x2+|x-a|+1,x∈R.
1)讨论f(x)的奇偶性;
2)求f(x)的最小值.
(2002年全国数学高考理科试题)
2.设a为实数,函数f(x)=2x2+(x-a)|x-a|.若f(x)≥1,
1)求a的取值范围;
2)求f(x)的最小值;
3)设函数h(x)=f(x),其中x∈(a,+∞),直接写出不等式h(x)≥1的解集(不需给出演算步骤).
(2009年江苏省数学高考试题)
4 学生思维停滞溯源
高中学生惧怕甚至不会分类讨论,笔者认为有以下几个方面的原因:
1)对用分类讨论思想解决问题的步骤性、有效性缺乏成功的体验.
2)对分类讨论的常见类型(①由数学概念引起的;②由性质、定理、公式的限制引起;③由数学运算和字母参数的变化引起;④由图形的不确定性;⑤由实际意义引起)还缺乏足够地认识和学习.
3)对分类讨论对象的分类标准还缺乏更多实际的经验.
回到本题,结合学生的反馈和笔者个人的理解,造成思维停滞的主要原因是忽略了参数对图像的“决定性”牵制,对参数的分类讨论是解决这类含参问题的着力点和必经点,对学生来说也是最难点.而生3有分类讨论的思想,但在对称轴和分段端点都变化的情况下,找不准参数的讨论临界点及对讨论的问题缺乏严谨性思考是问题关键所在.
5 教学思考
针对以上问题,笔者认为在平常的教学中要着重做好以下几个方面:
1)数学教学要“下得厨房,上得厅堂”.
数学教学中,有基本知识与基本技能的训练,更需有策略与思想引领的培养,数学思想则是数学中最顶层的东西.教师在平常的教学中不要仅会“下”些习题“小菜”,也要经常从中“上”升到思想方法的“厅堂”上来,只有提升学生的思维品质,才能达到居高俯瞰.
2)数学教学要“由点及面”.
通过解答一个典型问题的“点”进而推广扩散到“面”,借“题”发挥,由此及彼,引导学生,达到对一类题型及相关知识体系内涵关联的有效掌握,提升学生解题的全面性和思维的整体性.
3)数学教学要使学生“拨云见日”的能力不断提升.
“授人以鱼,不如授人以渔”.反复不断地试探学生是否掌握核心知识的方法和技能,教学应始终围绕提升“拨云”的剖析归类能力,让学生真正能独立思考和解决问题.
6 结束语
2015年的新高考,函数将更加归全反真,而二次函数作为函数家族的“当家花旦”,最有可能推到前台唱出高考好声音.因此,在二次函数的复习中,除了做好基本的图像性质、最值问题、“3个二次”的关系研究等基础问题和基本类型的复习工作外,还需对一些特殊类型的函数模型和特别的解题方法模式加以渗透和研究,只有做好平常的杜隙防微,才能在高考的战场上任性由我!
[1] 于亦香.对一道函数绝对值问题的探究[J].中学数学,2012(4):86.
