与有心圆锥曲线的共轭直径相关的一类轨迹问题

范伟峰 (天台中学 浙江天台 317200)



与有心圆锥曲线的共轭直径相关的一类轨迹问题

范伟峰 (天台中学 浙江天台 317200)

数学家波利亚认为：“一个重大的发现可以解决一道重大的题目，但是在解答任何一道题目过程中也会有点滴的发现.”近日，笔者在求解一道解析几何题时，就经历了这一过程，与读者分享.

图1

( )

片段1 笔者首先就此题给出了初步解答：

设P(x1,y1)，Q(x2,y2),则

即

x1x2+2y1y2=0,

片段2 对于一般的情形，设P(x1,y1)，Q(x2,y2),则

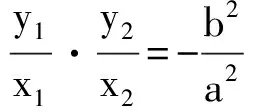
即

b2x1x2+a2y1y2=0.

我们也可以从变换的角度给出PQ中点N的轨迹的几何解释，从而更深刻地揭示该问题的本质．

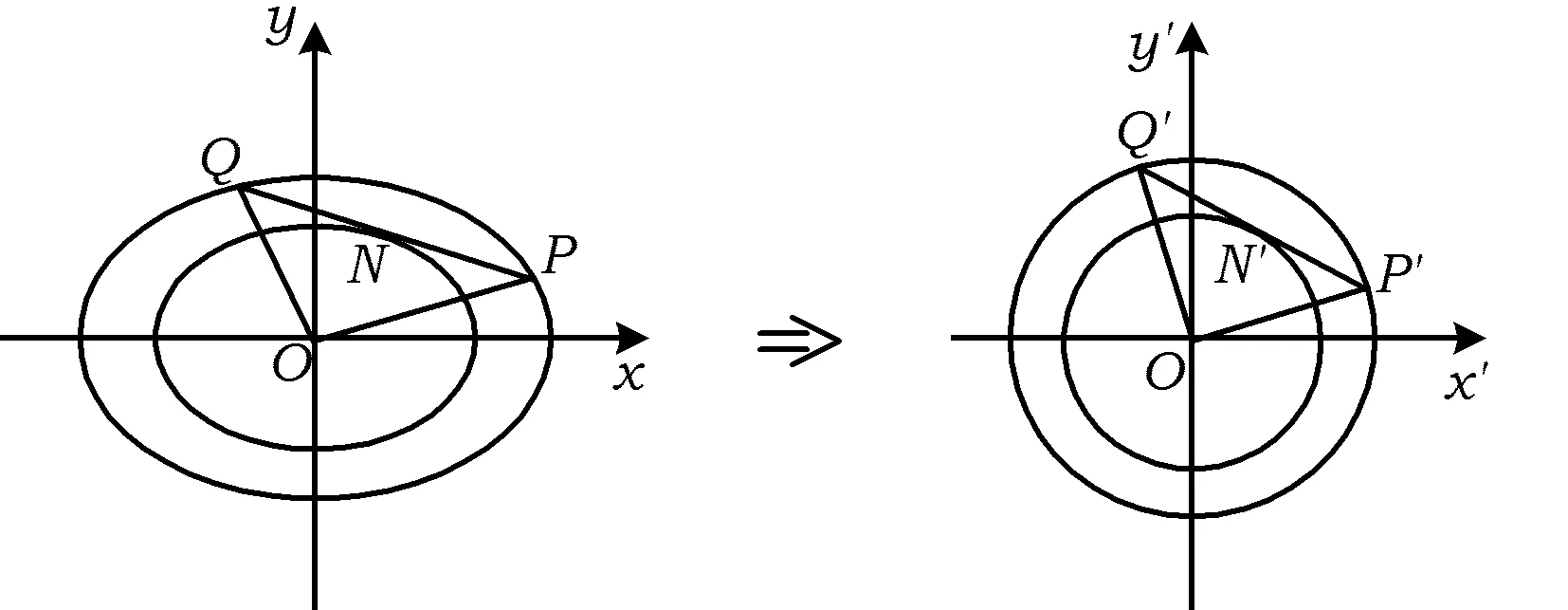
图2

将以上性质进行推广，得到了如下的性质：

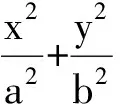
证明 设P(x1,y1)，Q(x2,y2),则

即

b2x1x2+a2y1y2=0.

由N(λx1+μx2,λy1+μy2)，令x=λx1+μx2,y=λy1+μy2，从而

b2x2+a2y2=b2(λx1+μx2)2+a2(λy1+μy2)2=

类似地，对于双曲线，有以下性质.

众所周知：双曲线的渐近线是退化了的双曲线，若P,Q是双曲线的渐近线上2个不同的点，也具有类似于上述的性质.

证明 设P(x1,y1)，Q(x2,y2),则

由S△OPQ=ab得

即

x1x2=a2.

由N(λx1+μx2,λy1+μy2)，令x=λx1+μx2,y=λy1+μy2,从而

b2x2-a2y2=b2(λx1+μx2)2-a2(λy1+μy2)2=

2λμ(b2x1x2-a2y1y2)=

2λμ(b2x1x2-a2y1y2)=

4λμb2x1x2=4λμa2b2,

每一个数学问题都有它的本质.面对一个问题，如果只看到它的表层，就无法深入到内核，从而看不透问题的本质，正所谓“不识庐山真面目，只缘身在此山中”.因此，在平时的解题和探究过程中，教师应通过问题的解决揭示问题的本质，使数学问题的解决变得简单而自然．

[1] 杜山,卢伟峰.椭圆共轭直径的一组性质[J].数学通讯，2008(15):19-20.

[2] 汤敬鹏.利用仿射变换解决与椭圆有关的高考试题[J].数学通讯，2010(4):44-46.