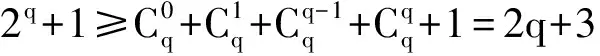简中求道
——利用二项式定理的放缩功能解题举例
2015-06-12杨元韡常州高级中学江苏常州213003
杨元韡 (常州高级中学 江苏常州 213003)
简中求道
——利用二项式定理的放缩功能解题举例
杨元韡 (常州高级中学 江苏常州 213003)
数学的简洁美是数学重要的美学特征.数学中有一些重要公式(如二项式定理表达式)结构对称,体现了数学公式的对称美.灵活运用它,可以简捷地解决某一类问题,其过程也体现出数学的简洁美.二项式定理可以把指数式放缩成适当的多项式(往往通过去掉某些正项的方式),从而可以简捷明快地解决以“底数大于1的指数函数比多项式形式的函数增长的速度快”为命题背景的问题.这类问题通俗地表达,就是当a>1时,函数y=an将随着n的增大会“爆炸式”地增大,如常用于励志的“1.01365≈37.8”正说明了这个道理.下面笔者给出利用二项式定理放缩功能解题的一些例子,说明二项式定理放缩功能的应用使得问题的解决更加简捷、漂亮.
1 利用二项式定理放缩证明数列不等式
在数列的综合问题中,常常出现求某个数列的最大项或者最小项,这类问题往往可以转化成考查数列的单调性问题.而研究数列单调性的基本方法有:作差法、作商法(正项数列)、考察相应函数的单调性(利用导数研究函数的方法)等.对于通项公式为an=an-g(n)(其中常数a>1,g(n)是关于n的多项式)的数列{an}项的符号判断,可以尝试使用二项式定理放缩来解决.

1)求an和bn.
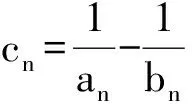
①求Sn;
②求正整数k,使得对任意的n∈N*,Sk≥Sn.
(2014年浙江省数学高考理科试题)
分析 我们主要研究第②小题,其实质是求{Sn}最大项的项序号.为此,可采用作差法研究{Sn}的单调性,即判定Sn-Sn-1(其中n≥2)的符号,亦即判定cn的符号;再利用作差法研究数列{cn}的单调性即可.根据数列的结构特点,也可以尝试使用二项式定理解决.
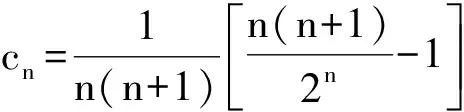

因此,当n≥5时,cn<0.
综上所述,对任意的n∈N*,S4≥Sn,即k=4.
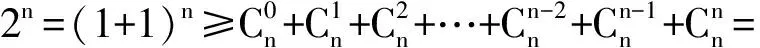
n2+n+2>n(n+1),
这里n≥5,故2n展开式至少有6项,从而
综上所述,对任意的n∈N*,S4≥Sn,即k=4.

2 利用二项式定理放缩证明函数不等式
我们知道,形如f(x)=ax-g(x)(其中a>1,g(x)是关于x的多项式)的函数,只要x充分大,总会有f(x)>0.尽管这个模型是连续的函数模型,但有时可以先将它转化成离散模型(如数列模型),再利用二项式定理也能简捷明了地加以处理.
例2 已知函数f(x)=ex,g(x)=ax2+bx+c.
1),2)略.
3)若b=c=0,试证明:对任意给定的正数a,总存在正数m,当x∈(m,+∞)时,恒有f(x)>g(x)成立.
(2015年江苏省扬州市高三期末考试试题)
分析 本题实际上就是证明对任意给定的正数a,存在正数m,当x∈(m,+∞)时,恒有ex>ax2.常规的方法是利用导数的方法解决,为此需要构造新函数来处理,但需要多次构造函数.但基于这2个函数结构的特殊性,也可尝试使用二项式定理来解决.
证法1 当0
x>2lnx+lna.
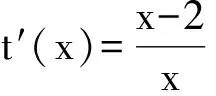
t(x0)=e2a-4-3lna>7a-4-3lna>
4(a-1)+3(a-lna)>0,
这里实际上还需要证明a-lna>0,即存在m=ae2,当x∈(m,+∞),恒有f(x)>g(x)成立.
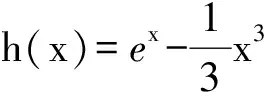
证法3 考虑x>6,并设n≤x ex>2x≥(1+1)n= 待证不等式右边可以放大,作如下放缩: ax2 (注意当n≥6时,有n+1<2n-4). 从而取m=max{6,24a+3},当x>m时,有ex>ax2. 评注 证法1和证法2都是利用导数的符号去研究函数的单调性,需要多次构造新的函数,不断研究这些新的函数,最后获解,但相对而言证法1的取值是比较困难的.证法2和证法3的共同之处在于,插入了一个三次多项式结构的中间量:证法2利用导数巧妙地证明了ex大于一个三次多项式函数,再证明当x充分大时,三次多项式函数大于二次多项式函数;证法3先把连续的函数放缩成离散的数列模型,待证不等式的左边缩小成关于正整数n的三次多项式,右边放大成关于n的二次多项式;证法3的优点是简洁,回避了所有函数的求导问题. 在数列问题中,常常出现判断某个值是不是该数列中的项,或者数列中是否有某3项成等差(或等比)等问题,这类问题最终都可转化成某些方程是否有正整数解的问题.如果这个方程中既有形如an(其中a>1),又有形如关于n的多项式g(n),则可以根据二项式定理判断当n充分大时该方程不成立,从而控制n的范围,再通过枚举验证方程是否有正整数解,或者求出正整数解. 例3 设{an}是公差为d的等差数列,{bn}为公比为q(其中q≠1)的等比数列,及cn=an+bn. 1)略. 2)若数列{cn}的前4项分别是4,10,19,34. ①求数列{an}和{bn}的通项公式; ②是否存在元素均为正整数的集合A={n1,n2,…,nk}(其中k≥4,k∈N*),使得数列cn1,cn2,…,cnk为等差数列. (2015年江苏省南通市期末考试试题) 分析 我们主要研究第②小题,易得an=3n-2,bn=3·2n-1,从而cn=3·2n-1+3n-2.问题中问的是数列{cn}中是否存在至少4项依次成等差数列,不妨考虑项数最小的情形,即假定{cn}恰有不同的4项成等差数列,设这4项分别为cp,cq,cr,cs(其中p (1) 方程右边的最高次幂为r-1(显然r-1≥q). 当2r-1>2q时,即2r-1≥2q+1,方程(1)的右边为 2r-1+2p-1-2q≥2q+1+2p-1-2q=2q+2p-1≥ (此处q≥3,二项展开式至少有4项),而方程(1)的左边2q-p-r<2q,故方程(1)不成立.当q=2时直接验证可知也不成立. 通过上面的分析,我们知道2r-1=2q,即q=r-1,同理可得s=r+1.由cr-1,cr,cr+1成等差数列得到2cr=cr-1+cr+1,化简得2r-2=0,矛盾.因此,可以知道不存在元素均为正整数的集合A满足条件. 上述得到矛盾的关键是紧紧抓住方程(1)右边的最高次幂,因为它的增长速度是最“快”的.利用二项式定理把它放缩成比方程左边大的多项式即可得到矛盾.但放缩时要注意项数,当q≥3时至少4项,可以直接导出矛盾,而当q=2时单独检验即可. 总之,二项式定理在处理指数函数比多项式函数增长得“快”为命题背景的问题中往往能起到化繁为简的效果.在使用二项式定理的放缩功能的过程中要注意2点:1)指数的大小要适当,例如展开式需要保留多少项,需要删除多少项,这些都要跟指数相关,指数至少要比展开式的所有项的项数多1(二项式定理本身也说明这一点);2)明确放缩的方向,也就是明确保留的项(多项式)的最高次是什么,例如3个例题中保留的项的最高次数分别为2次、3次、1次.若能利用二项式定理处理这类问题,并结合刚才给出的注意点,仔细分析,往往能事半功倍! 数学教育的基本功能之一是培养学生的数学求简意识,数学也正因为有着简单的一面才熠熠生辉,令人折服!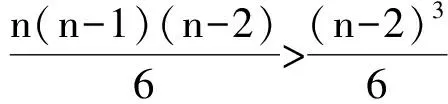
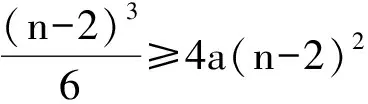
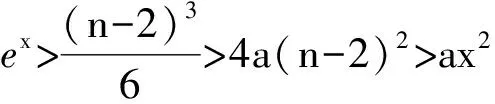
3 利用二项式定理放缩判断方程的解的问题