拂案坐去衫不冷 踏花归来马蹄香*——谈谈参加赛课的过程性思考

史 嘉 (亳州市第一中学 安徽亳州 236800)



拂案坐去衫不冷 踏花归来马蹄香*
——谈谈参加赛课的过程性思考

史 嘉 (亳州市第一中学 安徽亳州 236800)

笔者多次问自己：为什么要参加赛课？

从2013年4月学校选拔，到市，再到省，最终2014年12月7号到重庆参加第7届全国高中青年数学教师优秀课展示，在这近2年的时间里，笔者先后打磨了3个课题：“正弦定理”、“直线与平面平行的判定”和“函数的单调性”.现结合这3个课题谈谈个人对备课的思考和赛课收获，其中教训多于经验，仅供同仁参考，更期待批评指正.

1 理解学生比理解数学更“重要”

针对新课改下的数学教学现状，章建跃老师概括出指导教学的三大法宝——理解数学，理解学生，理解教学.我们知道“‘理解数学’是当好数学教师的前提”，但从参加比赛的角度说，理解学生比理解数学更要先行，甚至可以说更重要一些.因为课题一般都是举办方提供的，虽然他们在选择课题时会考虑承办学校的进度，但不同班级还是有差距的.

省赛时，笔者抽到的课题是：直线与平面平行的判定,这是北师大版教材第5节的内容.但笔者所任教的班级才刚刚开始学习“立体几何初步”，学生没有学习“直观图”、“三视图”、“空间图形的基本关系与公理”，连直线与平面有哪些位置关系都还没学，如何学习“平行关系”(直线与平面平行)呢？上课前才了解到学情，致使笔者一时乱了阵脚，“复习回顾”成了“学习新知”，即便极力调整教学程序和教学速度，“预设与生成”也难免大打折扣.

曲高自然和寡.因此，比赛前最好能先了解一下所任教班级的教学进度和学生的上课状态.备课要先备学情，理解学生比理解数学更“重要”.

2 构思教学设计要创新，更要继承

俗话说，巧妇难为无米之炊.这“米”便是各种资源，但有了“米”，若想做出特色，需要先熟知已有做法，才能推陈出新.因此，确定课题后(即使临时抽题，也会提前给备选课题)，除了要研读教材和教参，还要围绕课题搜集相关案例和课件等.海选不可取，建议从中国知网上筛选.因为能够发表的文章都饱含作者的心血，或多或少都有可借鉴之处，根据自己的教学需要和风格甄选、整合、深加工.

图1

设计“直线与平面平行的判定”时，笔者看到一个案例，在探究判定定理前先给出问题：请你判定直线与平面是怎样的位置关系(配图1，平面上斜放一条直线).感觉此题很好，不仅让学生感受到线面平行定义的“中看不中用”——不可操作性，直观感知不可靠，而且还自然引出定理的探究.在此基础上笔者设计了如下学习单.

学习单1 你相信自己的眼睛吗？

在带领学生一起观察身边的实例(红绿灯横梁与马路、单杠与地面、足球门横梁与操场、日光灯与天花板等)后，“回顾”线面平行的定义，接着推出“学习单1”，问：“直线a与平面α平行吗？”学生七嘴八舌，通过举手自然把学生分成3组：认为平行、相交和不置可否.然后发挥多媒体动态优势——延长直线作成相交的效果，平移直线作成平行的效果.总结出“你的眼睛欺骗了你的心，”紧跟着追问：“眼见都不一定为实，该怎样判定直线与平面平行呢？”开启探究之旅.

3 “用教材教”的教材总共有6套

本次课改倡导“不是教教材，而是用教材教”和“创造性地使用教材”的理念，这对教师提出了较高的要求.理念中的“教材”应该包括5套课标教材(人教A版、人教B版、北师大版、苏教版、湘教版)和上教版教材，这些都是备课所需要参考的.把6套教材对比学习是一件特别有意义的事，对相同内容的不同或近似的组织和讲述方式定会给我们启发，选择例题和练习题的空间也大了许多.

根据教学设计的需要，笔者选择了后者.原因有3个：1)函数解析式是分式形式，更具有示范的价值；2)解释物理学中的定律，锻炼学生的应用意识；3)题中“当体积V减小时”与单调性定义中“随x的增大”的表述方向相反，能发散学生的思维.

因此，选择案例固然重要，但研读各版本教材才是根本.

4 创设的情境需要做到“3个贴近”

常言道，良好的开端是成功的一半.确实，一个好的问题情境能迅速抓住学生，激发其学习兴趣，达到“转轴拨弦三两声，未成曲调先有情”的效果.教师常为此殚精竭虑，这或许也是“万事开头难”的原因之一吧.

好情境至少要做到“3个贴近”：1)贴近学生.是指贴近学生的知识经验和生活经验，贴近学生的思维水平.学生身处熟悉的情境容易启动思考，思维也活跃.2)贴近数学.是指具有数学味，贴近数学本质.好情境要蕴含数学概念、定理和公式的胚胎或雏形，能揭示数学的本质和思想，不仅能把学生引到问题的起点，而且为学生开启探究之路，即具有思考性.3)贴近教学.情境是为课堂教学服务的，要有利于学生对数学的理解，达成预期的教学目标.因此，创设的情境要具有教学性，即典型、简短、明了、易操作，兼顾文化性和趣味性.

图2

在设计“正弦定理”时，笔者借鉴下面这个问题开始探究.

引题 如图2，在△ABD中，AB=AD，C为BD边上一点，分别作△ABC和△ACD的外接圆.问：2个外接圆的大小关系如何？为什么？

从实际教学效果看该情境还是不错的，能把学生推向“愤悱”状态，达到了预期的目的.不过，有些教师一语点中其软肋——“复杂化了”、“不自然”.毕竟三角形的外接圆及其半径是三角形的相关要素，完全可以从其基本要素(边、角关系)入手——从定性到定量.情境只是情境，即使“数学归纳法”经典的引入情境(多米诺骨牌游戏)也有其不足：不满足命题P(n)的无限性.这确实值得我们再思考.

5 明确“教”的目标性和“学”的必要性

课堂教学目标是一节课的指南针，时刻指引着课堂教学的方向.对此，我们都能给予足够的重视.但是，特征鲜明的“三维目标”容易使课堂教学目标流于形式，定向和矫正功能不强.因此，科学合理的课堂教学目标应强调具体化、可操作和可检测，还要以具体知识为载体体现数学思想.

与“教”的目标性相比，“学”的必要性也是需要课前思考的，但多数时候并没有得到足够的重视.比如学习函数的单调性，“图像上升或下降”直观明了，“y随x的增大而增大或减小”通俗易懂.处理问题一路顺风顺水，学生心中难免会产生疑问：为什么高中要学习函数单调性的形式化定义？为解学生心头疑惑，笔者特意设计如下认知冲突情境.

图3

学习单2 设置问题，形成冲突

1)图3是函数y=f(x)的图像，它在定义域R上是递增的吗？

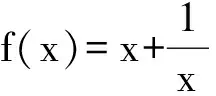
教学时先提出问题1)，学生回答后给出此函数图像的解析式f(x)=0.001x+1.再推出问题2)，学生会不置可否，或者凭感觉猜测，可追问其判定依据.

问题1)说明函数图像虽然直观，但是缺乏精确性，必须结合函数解析式；问题2)说明单凭解析式常常也难以判断其单调性.以此得出“函数图像不可靠，解析式也不明朗”的结论，让学生意识到学习的必要性，为形式化定义的出场“造势”.

6 在教学重、难点处要“舍得下功夫”

根据教学内容和课堂教学目标，每一节课都有“轻重缓急”之分.因此，设计教学程序应“因材施教”，在重、难点处要本着“高立意、低起点、小跨度、多层次”的理念，做到“不惜时、不惜力”，浓墨重彩绘重点，抽丝剥茧破难点.

以“函数的单调性”为例，难点(亦重点)是：如何突破用静态的数学符号刻画动态的函数变化趋势.“不断改进教学方法唯一直接的途径，就是把学生置于必须思考、促进思考和考验思考的情境之中……困惑是思考的不可或缺的刺激”(杜威语).基于此，我们设计了下面的问题串.

学习单3 引导探索，生成新知

1)如何理解“y随x的增大而增大”，怎样用数学符号描述函数图像的“上升”特征？

设计说明 以函数f(x)=x2(其中x≥0)为例，用几何画板演示“y随x的增大而增大”，生成表格，引导学生抽象出：若x1

2)已知a

设计说明 给学生充足的时间思考，交流后，拖动“点M”改变函数y=f(x)在区间[a,b]上的图像，验证2个定点并不能确定函数的单调性.

3)已知a

设计说明 拖动“点M”验证3个点也不行.那么，很多点、无数个点行不行呢？引导学生体会取值的“任意性”.

4)已知a

设计说明 先请赞同者说明理由，再请反对者画图反驳.有意引发争论，促进理解.追问：无数个x也不行，那该怎么办？若学生回答取完或任取，追问：总不能一一验证吧？

5)教材中子集的概念(略).

设计说明 PPT展示概念的截图，提取出“任意……都……”的表达句式.唤醒已有认知经验，寻找知识的固着点.

7 精品课必须经历打磨、打磨、再打磨

公开课、比赛课等常被人诟病为作秀课、假课，甚至有人偏激地认为：参加赛课，只需要练好普通话，至于怎么设计教学那是智囊团的事.致使此类看法的主要原因可能是认为翻来覆去的磨课，远离了常态课，演戏的成分大，指导意义不强.其实打磨的过程正是自我反思、自我总结、自我完善的过程，能促使青年教师专业化快速成长.

事实上，无论课前准备多充分，都不如进课堂检验一次，完整地、放开地试讲一遍，成败得失便知十之八九.修改后再试讲时，一定要请指导老师听课，最好请3位左右，这样讨论针对性强，而且高效.建议用录音笔录下整节课和评课教师的“狂轰乱炸”，他们不经意的一句话可能就会让你豁然开朗，或启发出奇思妙想.若能定稿，第3次试讲最好录像，方便全面“纠正”语言零碎、倾听不力、表情僵硬、手势凌乱、走位不周等现象，包括时间的安排、课件的合理性等.好课是从课堂中磨砺出来的.一般，课磨5遍为宜，太少心理不踏实，太多自己也就没了激情.

通过打磨，我们磨出了对教材深刻的理解，磨出了富有创意的设计，磨出了因势而变、顺学而导的驾驭力；磨掉了不经意的口头禅、表达不清的乱说、指向不明的乱问，磨掉了干扰学生思考和打断学生回答的抢话，磨掉了只想上完不管教学效果的赶课，磨掉了目中无生和原地不动的自我陶醉.

8 精彩的生成需要精心的培育

课堂教学具有动态性和生成性，也因此充满挑战性，这恰是课堂教学的魅力所在.正如叶澜教授所言：“课堂是向未知方向挺进的旅程，随时都可能发现意外的通道和美丽的风景，不会是一切都必须遵循固定路线而没有激情的行程.”

经过几次打磨，一节课的“预设生成”和“意外精彩”教师心中应该是有数的.如何把这些“生成”和“精彩”尽可能多地集中到一节课上，需要我们精心地培育和耐心地引导.

比如“函数的单调性中学习单3问题4)，该问题思维空间很大，是学生争论最激烈的地方，是突破难点的关键，也是所谓的亮点或出彩之处.在学生讨论交流时，教师需要深入学生，摸清哪些学生持赞同观点，在学生交流时有意先请他们发言，如此定会“一石激起千层浪”，激活反对者的发言欲望和激情，于是出现激烈交锋场面.若僵持不下，可请旁观者出手相助，问题越辩越明朗.精彩的生成也就在精心的培育下自然绽放了.

9 自述要“述”教学构想、突破过程及效果

全国赛课是以录像课展示和自述的形式进行的.有30分钟的时间限制，因此更要思考展示什么、自述什么.通常，除了“述”教学内容解析、学生学情分析、课堂教学目标和教学反思，更重要的是“述”教学策略分析，并具体到教学过程中展示，以视频佐证教学构想、突破过程和教学效果.把45分钟剪辑成25分钟，是一个痛苦的割舍过程，不可能把所有环节都展示，因此要选择必要的、突破难点的、反映独特设计思想的、精彩的环节展示.比如，函数单调性形式化定义的突破，笔者足足用了12分24秒(视频总长23分22秒)连续播放，把“核心”部分如实展示.

自述和教学基本一样，要力求语言准确、简洁、口语化、抑扬顿挫、有感染力及亲和力，过渡合理，衔接自然，手势等肢体语言得体、大方.同时，自述还要力求条理清晰、节奏明快，脱稿而不背稿.当然，幽默风趣也是我们追求的，但要贴合整体教学风格，不恰当的幽默宁可不要.比如在讲授线面平行“学习单2”时，说到“线面平行的定义‘中看不中用’”，其实笔者想表达的意思是定义不具有操作性，但专家质疑：“一切都是从定义出发的，怎么能说‘不中用’呢？”再比如，在全国展示时笔者被安排在B组第一个，是否可结合单调性就此幽默一把？一来缓解紧张情绪，二来调动会场气氛.于是拟定开场：“尊敬的评委、各位老师，大家上午好！我是……非常荣幸能作为我们B组这个递增区间的左端点.”征求几位教师的意见后放弃了.主要是担心评委和教师会不会感觉莫名其妙；中间选手会不会想：凭什么说我不是最大值；评委会不会想：你不是在暗指我们的打分会越来越高吗？更致命的是，B组是区间吗？没有十足的把握，宁舍毋滥.

10 教学课件要实用、简洁、不喧宾夺主

最后说说课件.此类课要使用多媒体是不成文的规定，既然必须使用，那就把信息技术的优势发挥到淋漓尽致.

信息技术在展示、计算、绘图、动态和直观等方面是传统教学手段无法比拟的，大大提高了数学的教学效率和效果.但是，信息技术只是辅助工具，使用的唯一原则是有利于学生对数学的理解和掌握.这要求我们要深入“理解技术”(继“3个理解”之后的第4个理解).除传统的投影仪外，数学教学最常用PPT、几何画板、Excel、图形计算器等工具.在了解各软件优势的基础上，设计教学程序时，要先考虑好哪些环节可不用、可用、必须用、用什么、怎么用等问题，还要注意教学多媒体和传统手段的“组合运用”.

针对PPT的使用，应注意以下几点：1)课件整体颜色鲜明，干净大气，要统一风格；2)一页内容不能太多，字体颜色和背景对比清晰，32号黑体且加粗为宜；3)要尽可能地减少点击次数，使用翻页笔播放；4)推出或退出方式不宜太花哨，最好不要添加声效；5)一定不要有小马等动画不停地播放，容易分散学生的注意力；6)若需要用几何画板等，镶嵌的效果好于链接，上课前可先打开几何画板；7)注意各版本的兼容性，以防课件变形，甚至打不开.因此，调试课件时一定要一项一项地播放，还要注意“屏幕分辨率”的匹配情况.

结束语 为什么要参加赛课呢？笔者的理解是：虽然说“教学永远是一门遗憾的艺术”，但教师的一生总得有一节至少让自己满意的课吧.事实上，赛课是最好的学习方式之一，是促使教师专业化快速成长的一条快捷通道.教学切忌“轻过程、重结果”，赛课也是一样.只要我们用心做“拂案坐去衫不冷”的过程，“踏花归来马蹄香”的结果便是水到渠成般的自然.

[1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003.

[2] 曹才翰，章建跃.中学数学教学概论[M].2版.北京：北京师范大学出版社，2008.

[3] 曹才翰，章建跃.数学教育心理学[M].2版.北京：北京师范大学出版社，2007.

[4] 章建跃.中学数学课改的十个论题[J].中学数学教学参考：上旬，2010(1/2):3-6.

[5] 章建跃.中学数学课改的十个论题(续)[J].中学数学教学参考：上旬，2010(3):2-5;11.

[6] 章建跃.中学数学课改的十个论题(续)[J].中学数学教学参考：上旬，2010(4):2-6.

[7] 章建跃.中学数学课改的十个论题(续)[J].中学数学教学参考：上旬，2010(5):2-5.

安徽省教育规划课题《“文化数学”理念下高中数学学习单的实践研究》(项目编号：JG13105)和《基于基本活动经验的高中数学教学实践研究》(项目编号：JG14071)的阶段性研究成果.