基于统计模型的非饱和土渗透系数函数研究

王晓峰，时红莲，唐志政，牛超颖

（1.中国地质大学（武汉）工程学院，武汉 430074；2.山东正元建设工程有限责任公司，山东烟台 264670）

基于统计模型的非饱和土渗透系数函数研究

王晓峰1，2，时红莲1，唐志政1，牛超颖1

（1.中国地质大学（武汉）工程学院，武汉 430074；2.山东正元建设工程有限责任公司，山东烟台 264670）

对比分析2种基于统计模型预测非饱和土渗透系数的方法（Kunze法与Fredlund法），得出：2种方法本质相同，仅选取的积分限和积分变量形式不同，是对同一问题的2种不同表述。对其简化计算方法中各参数的选取进行深入分析，结果表明：分段数m取值介于15～50时较为合理，且Fredlund方法中取ln（1 000 000）（假定残余含水率为0）为积分上限、进气值的对数为积分下限，理论上会使预测结果偏大。当接近饱和含水率时，非饱和渗透系数随含水率的变化较为敏感，当接近残余含水率时，渗透系数变化率很小且差异性趋于不明显。

非饱和土；渗透系数；统计模型；Kunze法；Fredlund法；残余含水率

2015，32（01）：102－105

1 研究背景

作为土力学的3大经典问题之一，渗流问题一直倍受关注。现有的研究大都限于饱和土，有关非饱和土渗流特性的研究相对较少，尤其是受到实验条件的限制。为此，前人开发了很多数学预测模型，主要有经验模型、宏观模型、统计模型和分形模型。经验、宏观模型需通过多组实测数据求解拟合参数，仍不能摆脱试验条件的限制，分形理论在这方面应用时间较短，预测结果有待检验，而统计模型因其推导过程严谨、预测准确等特点被不断完善和发展。统计模型假定，在土体中孔径为ri的孔隙频率分布函数为f（ri），并且对于每一个特定尺寸的孔隙，认为Hagen-Poiseuille方程成立，则对所有孔隙进行积分就可得到土体的渗透系数 K。同时假定，基于Kelvin毛细模型，非饱和土的土水特征曲线可以表征其孔隙频率分布函数。于是，在土－水特征曲线已知的情况下，以孔隙频率分布函数作为中间函数可推导出渗透系数曲线。

基于该理论，国内外学者开发了众多预测方程，尤其是Kunze修正方法［1］（1968）和由此延伸出的Fredlund（1994）方法［2］被广泛应用于实际工程和科研。叶为民等［3］利用Fredlund方法预测了上海非饱和软土的渗透系数，并认为：虽然以进气值作为积分下限，但实际上任何0到ψaev之间的值都可以使用，换言之，没必要知道精确的进气值。张锐等［4］利用Kunze修正法预测了广西宁明2种膨胀土的原状样和重塑样的非饱和渗透系数，进而得到了非饱和膨胀土的含水量－渗透系数关系及其变化规律。张红芬等［5］利用Kunze修正法对黄河大堤非饱和土的渗透系数进行预测，跟实测结果对比发现当体积含水率为7%～23%时，直接法和间接法所得渗透系数比较接近。围压200 kPa条件下，当体积含水量等于0.13时，相对误差为0；大于0.13时，相对误差为负，即间接法所得渗透系数小于实测值；小于0.13时，相对误差为正，即间接法所得渗透系数大于实测值。随后李小伟等［6］、梁艳等［7］、常波等［8］等利用Kunze修正法分别研究了密度对非饱和土渗透系数的影响、临江Ⅱ号崩滑堆积体的滑带土及滑体土的渗透特性和晚更新世黄土竖直与水平方向的非饱和渗透系数分布规律。

可见，统计模型方法为研究非饱和土的渗透特性带来了便利。但在应用过程中依然存在很多问题，如：分段数m的确定、土－水特征曲线拟合公式及积分限的选取等。为研究这些因素对预测结果的影响，本文通过选取不同参数值对渗透曲线的变化规律做了深入分析，并对2种常用方法进行了评价。

2 方法解析与简化

2.1 Kunze法与Fredlund法的联系与区别

Childs和Collis-George［9］（1950）最先提出渗透系数K与不同孔径连通率函数之间的关系式，Marshall［10］（1958）将其理论扩展得到一个饱和渗透系数函数，结合Young-Laplace方程推导出了非饱和土的渗透系数表达式，并最终由Kunze等（1968）进行修正，其相对渗透系数的积分形式见式（1）。

式中：Kr为相对渗透系数；θL为试验土－水特征曲线上最低的体积含水率（一般取θr）；θs为饱和含水率。

Fredlund发现，在应用上述方法时必须求得残余含水率，而通常情况下该值并不易获取。Croney and Coleman［11］（1961）实践和Richards［12］（1965）理论证明，对于不同类型土体0含水率所对应的吸力值是一个常数，约为106kPa。于是，Fredlund和Xing［13］（1994）提出一个描述土－水特征曲线在整个吸力范围内（即0～106kPa）的总方程为

式中：e为自然数；a为土的进气值；n为控制土－水特征曲线中拐点处斜率的参数；m为与残余含水率相关的参数；C（ψ）为修正因子，可使模型能够表征0含水率时的吸力值为

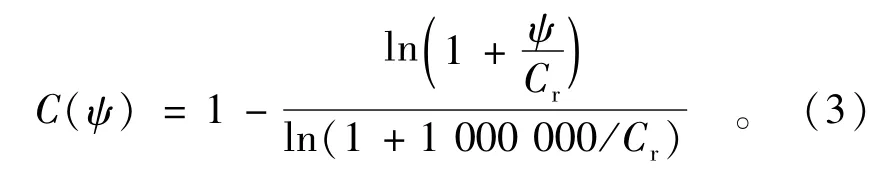
式中：Cr是残余含水率状态时的吸力值（kPa），Fredlund-Xing模型假定残余含水率为0。若考虑的是整个吸力范围，则体积含水率以0含水率为基准，从而避免求解残余含水率。最终将式（1）化为式（4），即

式中：ψaev为进气值；b＝ln（1 000 000）；y为吸力对数的积分虚拟变量。

分析可知，Kunze法与Fredlund法本质相同，都是由土－水特征曲线，以相同孔隙分布概率函数作为过渡准则推导渗透系数曲线，是同一问题的2种不同表达形式。同一土体在同一路径上的土－水特征曲线客观存在，具有唯一性，若拟合效果足够准确，不管选用何种形式的方程，不影响积分结果。Kunze法的积分区间为θL～θs，Fredlund法的积分区间为ψaev～ln（1 000 000），用含水率表示为0～θa（θa为进气值对应的含水率，其值小于θs）。由此看出，2种方法的本质差别在于积分区间两端位置的选取不同。并且，当积分区间取值相同时，Kunze法与Fredlund法完全等效，只不过前者是以θ为积分变量，而后者是以lnψ为积分变量。根据相关数学理论，积分结果与积分变量的选取无关。

2.2 简化计算方法

Kunze法与Fredlund法本质相同，均可通过以下简化形式求解［14］：

式中：Kw（θw）i为用相应于第i个间段的体积含水率（θw）i确定的水渗透系数（m/s）；i为间段编号，随体积含水率的减小而增加，例如，当i＝1时，表示第一个间段，即紧靠最大体积含水率 θmax（理论上θmax＝θs）；当i＝m时，则表示最末一个间段，相应于试验土－水特征曲线上最低的体积含水率θL（理论上θL＝θr）；j为从“i”到“m”的某个数；m为在土－水特征曲线上，从最大体积含水率θmax到最低体积含水率θL的间段点总数；Ks为实测饱和渗透系数（m/s）；Ksc为计算饱和渗透系数（m/s）；ua为非饱和土体内孔隙气压力（kPa）；uw为非饱和土体内孔隙水压力（kPa）；Ad为调整常数，该计算值不会影响Kw（θw）i的最终值，具体请参阅文献［14］。

该方法将土－水特征曲线沿体积含水率轴分成m等份，如图1所示，相应于每一个等分中点的基质吸力可用于计算渗透系数。计算过程中，假设统计模型理论成立且土－水特征曲线方程足够准确，则m值的确定，积分上、下限的选取是影响预测结果的主要因素。

图1 根据土水特征曲线预测渗透系数Fig.1 Prediction of hydraulic conductivity according to soil-water characteristic curve

3 参数选取对渗透系数的影响

3.1 “m”值对预测结果的影响

试验测定某黄土试样的土－水特征曲线方程见式（7），结合式（5）、式（6）计算出体积含水率与相对渗透系数的关系曲线见图2，计算时最大体积含水量取θs，最小体积含水量取θr，m分别取5，10，15，20，40。

由图2知，m＝5时，预测结果偏大，而m＞10时，预测曲线几乎重合。虽然理论上m取无穷大时最接近真实值，但实际，当m＞10，即使m成倍增加，曲线的预测精度提高很少。因此，利用简化的Kunze法或Fredlund法预测非饱和土的渗透系数时，m在 15～50范围内取值即可，既能保证预测结果的精确度，又可减少计算量，提高工作效率。

图2 体积含水率与渗透系数的关系曲线Fig.2 Relationship between volumetric water content and hydraulic conductivity

3.2 积分限对预测结果的影响

通常情况下残余含水率时水分类型以结合水为主，土体内水分运移主要以蒸汽形式进行，对应的渗透系数为0，因此，选取饱和含水率为积分上限、残余含水率为积分下限最合理。为研究上下限取不同值时对计算精度的影响，将各参数设置如表1进行分析，计算出的体积含水率与相对渗透系数关系曲线见图3。

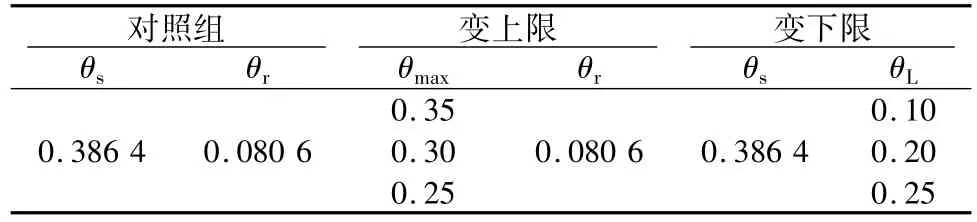
表1 参数设置表Table 1Parameter settings

由图3知，随积分上限θmax取值的减小预测值偏大，随积分下限θL取值的增大预测值偏小，且变化相同幅度，上限变化时预测结果严重偏离对照组，下限变化时偏离很小。可见，预测精度对上限的变化相当敏感，而下限的变化对预测结果影响较小。θL由0.080 6变到0.20时计算出的曲线几乎重合，只有当下限值变化幅度非常大时才会对计算结果产生明显影响。

图3 体积含水量与渗透系数的关系曲线Fig.3 Relationship between volumetric water content and hydraulic conductivity

Fredlund-Xing模型假定残余含水率为0，积分上限变为b＝ln（1 000 000），即该方法将0含水率作为渗透系数为0的基准点，而不是以残余含水率，换言之，残余含水率对应的渗透系数必然大于0，从而导致预测结果偏大。但通过图3分析可知，积分限θL取值的变化对预测结果的影响很小，即使偏大，其程度微乎其微，尤其对于残余含水率较小的土体。所以，Fredlund假定残余含水率为0，既避免了求解残余含水率又可保证预测精度。

同时，Fredlund将积分下限变为lnψae，对应的含水率为θa（小于饱和含水率θs），即该方法将进气值对应的含水率作为饱和渗透系数基准点，实际上该点渗透系数要小于饱和渗透系数，最终同样使预测结果偏大。分析知，当饱和度较高时，含水率的微小变化将导致渗透系数大幅变化，此时积分限的变化对预测结果的影响不能忽略。所以，在利用该方法进行计算时，应求出进气值对应的渗透系数Ka，则Kw（θw）i＝Ka×Kr，且仅能预测进气值以后吸力范围的非饱和渗透系数。

4 结 论

本文通过对比分析Kunze法与Fredlund法的联系和区别，得出以下结论：

（1）Kunze法与Fredlund法本质相同，都是由土－水特征曲线，以相同中间函数为过渡准则推导渗透系数方程，是同一问题的不同表述，Fredlund法虽然能避免求解残余含水率，简化计算，但理论上使预测结果偏大。

（2）在利用简化方法进行计算时，理论上m取值越大越精确，但实际中，当m＞10时，即使m成倍增加，预测精度提高并不明显，取值在15～50范围内即可满足要求。

（3）非饱和渗透系数在饱和度较高时对含水率的变化非常敏感，而当含水率接近残余含水率时，渗透系数变化率很小且差异性趋于不明显。

［1］KUNZE R J，UEHARA G，GRAHAM K.Factors Important in the Calculation of Hydraulic Conductivity［J］.Soil Science Society of America Journal，1968，32（6）：760－765.

［2］FREDLUND D G，XING A，HUANG S.Predicting the Permeability Function for Unsaturated Soils Using the Soilwater Characteristic Curve［J］.Canadian Geotechnical Journal，1994，31（4）：533－546.

［3］叶为民，钱丽鑫，白 云，等.由土－水特征曲线预测上海非饱和软土渗透系数［J］.岩土工程学报，2005，27（11）：1262－1265.（YEWei-min，QIAN Li-xin，BAI Yun，et al.Predicting Coefficient of Permeability from Soil-water Characteristic Curve for Shanghai Soft Soil［J］.Chinese Journal of Geotechnical Engineering，2005，27（11）：1262－1265.（in Chinese））

［4］张 锐，郑健龙，杨和平.宁明膨胀土渗透特性试验研究［J］.桂林工学院学报，2008，28（1）：48－53.（ZHANG Rui，ZHENG Jian-long，YANG He-ping.Permeability Test of Ningming Expansive Soil［J］.Journal of Guilin University of Technology，2008，28（1）：48－53.（in Chinese））

［5］张红芬，李永乐，刘翠然，等.非饱和土渗透系数直接试验法和间接计算法［J］.人民黄河，2011，33（4）：139－141.（ZHANG Hong-fen，LIYong-le，LIUCui-ran，et al.Method of Direct Testand Method of Indirect Calculation of Percolation Coefficient of Unsaturated Soil［J］.Yangtze River，2011，33（4）：139－141.（in Chinese））

［6］李小伟，王世梅，黄净萍.密度对非饱和粘土渗透系数的影响研究［J］.西北地震学报，2011，33（B08）：214－217.（LI Xiao-wei，WANG Shi-mei，HUANG Jing-ping.Influence of Density on Permeability Coefficient of Unsaturated Soil［J］.Northwestern Seismological Journal，2011，33（B08）：214－217.（in Chinese））

［7］梁 燕，邢鲜丽，李同录，等.晚更新世黄土渗透性的各向异性及其机制研究［J］.岩土力学，2012，33（5）：1313－1318.（LIANG Yan，XING Xian-li，LITong-lu，et al.Study of the Anisotropic Permeability and Mechanism of Q3 Loess［J］.Rock and Soil Mechanics，2012，33（5）：1313－1318.（in Chinese））

［8］常 波，吴益平，何高峰，等.临江Ⅱ号崩滑体土水特征曲线试验研究［J］.长江科学院院报，2012，29（9）：53－58.（CHANG Bo，WU Yi-ping，HEGao-feng，etal.Tests for Soil-Water Characteristic Curve of Riverside Slump-mass［J］.Journal of Yangtze River Scientific Research Institute，2012，29（9）：53－58.（in Chinese））

［9］CHILDS E C，COLLIS-GEORGE N.The Permeability of Porous Materials［J］.Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences，1950，201（1066）：392－405.

［10］MARSHALL T J.A Relation between Permeability and Size Distribution of Pores［J］.Journal of Soil Science，1958，9（1）：1－8.

［11］CRONEY D，COLEMAN JD.Pore Pressure and Suction in Soil［C］∥Proceedings of Conference on Pore Pressure and Suction in Soils.Institution of Civil Engineers.Butterworths，London，March 30－31，1960：31－37.

［12］RICHARDSL A.Physical Condition ofWater in Soil［M］∥Methods of Soil Analysis.Part 1.Physical and Mineralogical Properties，Including Statistics of Measurement and Sampling.Madison：American Society of Agronomy，1965：128－152.

［13］FREDLUND D G，XING A.Equations for the Soil-water Characteristic Curve［J］.Canadian Geotechnical Journal，1994，31（4）：521－532.

［14］FREDLUND DG，RAHARDJO H.SoilMechanics for Unsaturated Soils［M］.New York：John Wiley＆Sons，1993：256－278.

（编辑：王 慰）

Hydraulic Conductivity Functions for Unsaturated Soils Based on Statistical M odels

WANG Xiao-feng1，2，SHIHong-lian1，TANG Zhi-zheng1，NIU Chao-ying1
（1.Faculty of Engineering，China University of Geosciences，Wuhan 430074，China；2.Shandong Zhengyuan Construction Engineering Co.，Ltd.，Yantai 264670，China）

By comparing and analyzing twomethods（Kunze’smethod and Fredlund’smethod）based on statistical models to predicting the hydraulic conductivity of unsaturated soils，we found that they are exactly the same in essence justwith different limits of integration and integration variable forms.Moreover，by analyzing the selection of parameters in their simplified calculation we obtain that it ismore reasonable to determine the value of m within 15－50.Theoretically the prediction resultwill be larger if ln（1000000）（residualwater content is assumed to be 0）is taken as the integration upper limit and logarithm of air-entry value as the integration lower limit in Fredlund method.

unsaturated soil；hydraulic conductivity；statisticalmodel；Kunze’smethod；Fredlund’smethod；residual water content

TU411.91

A

1001－5485（2015）01－0102－04

10.3969/j.issn.1001－5485.2015.01.021

2013－08－21；

2013－09－26

国家自然科学基金项目（41272307）；教育部长江三峡库区地质灾害研究中心开放基金（TGRC201011）

王晓峰（1988－），男，山东滨州人，硕士，主要从事土－水相互作用机理研究和岩土工程设计工作，（电话）13655352233（电子信箱）964547554＠qq.com。

时红莲（1969－），女，河南郑州人，副教授，硕士，主要从事岩土工程性质的试验及基础工程设计工作，（电话）13871279685（电子信箱）shhl2000＠126.com。