基于最大加权信息熵模型的水污染物总量分配

刘 杰

（陕西理工学院数学与计算机科学学院，陕西汉中 723000）

基于最大加权信息熵模型的水污染物总量分配

刘 杰

（陕西理工学院数学与计算机科学学院，陕西汉中 723000）

为了建立公平有效的区域间水污染物总量分配机制，将信息熵概念应用在环境领域。以汉江发源地汉中市的水污染物COD（Chemical Oxygen Demand，化学需氧量）总量分配为例，充分考虑各区域自然和经济等因素的客观差异，选取与水污染物COD排放紧密相关的各项指标并将其量化，利用熵值法确定各指标权重，建立单位指标负荷污染物量的信息熵加权和最大的目标规划模型，最后利用智能的和声搜索算法求解得出更具公平性的削减方案。实验结果表明该方法能够通过量化多种公平性准则，根据各区域的实际情况得出优化可行的分配方案。为汉江水源地汉中的水质保护和COD总量控制提供了理论参考。

水污染物；公平分配；COD；总量分配；信息熵；最大加权；和声搜索算法；陕西汉中

2015，32（01）：16－20

1 研究背景

排污者都有排污权，但排污数量不能超过环境负荷。为了解决经济发展带来的水环境污染问题并且有效发挥环境资源利用率，早在20世纪70年代，美国联邦环境保护局便提出水污染物总量控制，逐渐成为有效改善水资源环境效用的管理办法。水污染物总量控制是我国实施水污染防治的重要举措，而污染物总量分配是实现总量控制目标的关键因素。在污染物总量确定的情况下，排污量分配方案与排污者自身利益息息相关，如何对污染物总量进行公平有效的分配从而实现经济发展和环境保护的双赢成为当前的研究热点。国内研究者们已经提出一些具体的分配方案，例如曹瑞玉［1］等以最小治理成本为目标建立了污染物总量分配模型；王有乐［2］运用多目标规划方法，建立了污染削减目标、最小治理费用，最大收益的多目标规划的数学模型；李如忠［3］等从经济、环境整体效益出发设计出一种多层次总量分配模型；盛虎［4］以最小控制成本为目标建立排污交易模型得到流域最优污染控制方案。本文将多种指标进行公平性量化，避免了分配的主观性，利用信息熵概念，建立最大加权信息熵的优化分配模型，并将该模型应用于汉江发源地汉中地区水污染物COD总量优化分配中。

2 信息熵在污染物总量分配中的应用

2.1 信息熵

“熵”是德国物理学家克劳修斯于1850年提出的概念，是热力学和统计物理学中特有的宏观量。它用来表示任何一种能量在空间中分布的均匀程度。系统的熵值和系统状态的无序度存在一一对应的关系，熵值越小，系统的状态越是有序，越不均匀；系统的熵值越大，它所处的状态越是无序，越均匀［5］。信息论之父C.E.Shannon在1948年发表的论文“通信的数学理论（A Mathematical Theory of Communication）”中将熵的概念引入信息论，称为“信息熵”。即对于一个不确定性系统，若用随机变量X表示其状态特征，对于离散型随机变量，设X的取值为X＝｛x1，x2，…，xn｝（n≥2），每一取值对应的概率为P＝｛p1，p2，…，pn｝（0≤pi≤1，i＝1，2，…，n）且有：，则该系统的信息熵为。

2.2 信息熵与污染物总量分配的公平性

在目前的水污染物总量分配中存在较多的人为因素，公平性如何进行量化存在很大争议。衡量公平的准则也分为需求类准则（经济、人口）和供给类准则（水资源量，水环境容量，土地面积）2大类。分配的公平性不是绝对的等量平分或者等比例平分，而是在充分考虑各地区经济、人口、水资源量、水环境容量等多项可以量化的公平性指标基础上实行统一规则的差额分配办法，从而实现分配的排污量与该区域客观因素的公平匹配，也就是虽然各区域的排放总量不同，但是各区域每个单位指标下的负荷污染物量相等。信息熵可以用来评价系统的均衡性，个体之间越是接近，表示他们的差异越不显著，信息熵值就越大，系统就越均衡［7］。因此，每项指标的单位负荷污染物量的信息熵值就反应了所选取指标的单位指标负荷污染物量的区域差异程度。单位指标负荷水污染物量的信息熵值越大，区域间的发展就越均衡，区域间的单位指标负荷污染物量的差异就越小。那么度量各区域单位指标负荷污染物量的差异程度就成为实现公平分配的关键问题。

2.3 熵值法确定权重

水污染物COD的排放量对不同的指标有不同的依赖程度。根据信息熵理论，信息熵是信息不确定性的度量，熵值越小，所蕴涵的信息量越大，若某个属性下的熵值越小，则说明该属性在决策时所起的作用越大，应赋予该属性较大的权重。对于给定的第j项指标，各区域的该指标值的差异性越小，那么该项指标的信息熵值越大，当所有区域的该项指标值全部相等时，该指标的信息熵值为最大值，即ej＝1，表示该项指标与污染物的排放量几乎毫无关系。相反地，当各区域某项指标值相差越大时，该指标的熵值越小，则该项指标与污染物排放量之间关系越大。根据文献［8］中利用熵值法来确定属性权重的方法，可以利用熵值法来确定某项指标在实行总量分配中的权重。依据指标的熵值大小ej与该指标下各区域的偏差程度相反的原则，定义指标j的差异因数即偏差程度系数为

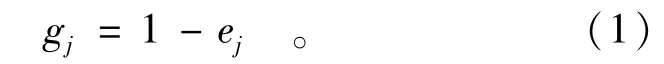
则当gj越大时，第j项指标就越重要，那么假设共有m项指标用差异因数gj来确定第j项指标的权重，即

3 基于最大加权信息熵模型的水污染物总量分配

3.1 量化公平性指标

根据衡量公平性的准则，本文选取与各区域水污染物排放量密切相关的人口、地区生产总值、水资源量和水环境容量作为4项基础指标。各区域的各个指标值如表1的指标矩阵所示。

表1 指标矩阵Table 1 M atrix of indexes

3.2 最大加权信息熵模型

3.2.1 优化模型

以各个区域的削减比例为决策变量，计算各指标的信息熵，利用熵值法确定各指标权重，并以各个指标信息熵值的最大加权和为目标函数，建立最大加权信息熵模型，即

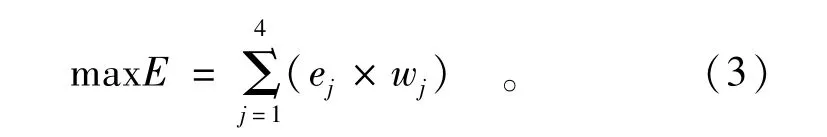
（1）计算不同区域各单位指标负荷的水污染物数量Xij，即

式中：Xij指第i个区域内第j项指标的单位负荷污染物量；qi指第i个区域的削减比例；W0（i）指第i个区域污染物排放量的现状值；Zij指第i个区域内第j项指标的值。

（2）计算第j项指标下第i个区域值在此指标中所占的比重Pij，即

（3）计算第j项指标的单位负荷污染物量的信息熵ej（这里采用的是实际信息熵与最大信息熵ln n的比值，将熵的取值范围修订在0～1之间，也就是说如果各个区县之间完全没有差异，即Pij＝1/n，则ej＝1；如果只有一个区域的熵值，其他区域全部为0，即Pij＝1，则ej＝0），即

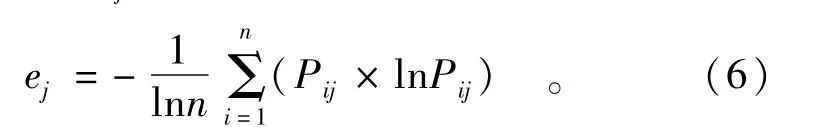
（4）熵值法确定各指标权重wj，即

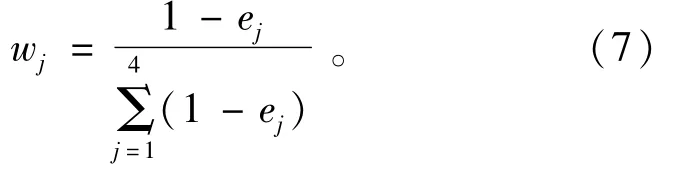
3.2.2 约束条件

（1）总量削减目标约束为

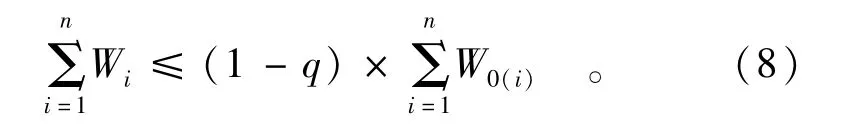
式中Wi指分配给第i个区域的污染物排放量。

（2）各区域可行的削减比例约束为

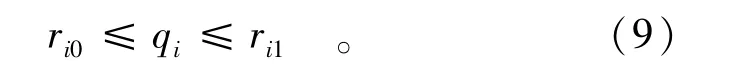
式中：ri0指第i个区域削减比例的下限；ri1指第i个区域削减比例的上限。

4 实例应用

4.1 简 介

汉中乃汉江发源地，汉江是长江的最大支流，全长1 577 km，总流域面积15.1万km2，其中汉中境内长270 km，大小支流共计346条，境内流域面积1.97万km2，占全市国土面积的72.3%，年平均径流量100亿m3。同时，汉中又作为南水北调中线工程和引汉济渭工程的重要水源地［9］，随着社会和经济的发展，汉江流域汉中段水质由70%的优Ⅱ类水质逐步转为Ⅲ类水质，因此本文以汉江流域汉中段各区域的水污染物总量分配为研究对象，采用该模型对汉中市的11个行政区域的水污染物总量分配方案进行评估和案例分析，为下一个五年计划汉中地区实施更具公平性的区域总量分配方案提供参考和指导意见。

4.2 技术方案及基础数据

4.2.1 技术方案

“十二五”期间国家要求总量控制的主要水污染物仍然为化学需氧量（COD），因此本文也以COD的区域总量分配为研究对象。根据《国民经济和社会发展“十二五”规划》，计划到2015年全国的主要水污染物排放总量比2010年减少10%，即总量削减比例q＝10%，最终各县区的分配结果就取决于各县区的削减比例，根据不同区域的实际情况，为了保证削减方案能有效实施，本课题提供3组不同的削减比例上下限，在具体实施总量分配时供决策者参考选择：①ri0＝1%，ri1＝15%；②ri0＝1%，ri1＝25%；③ri0＝1%，ri1＝30%。

本研究按照如图1的技术路线进行水污染物总量分配方案的研究。

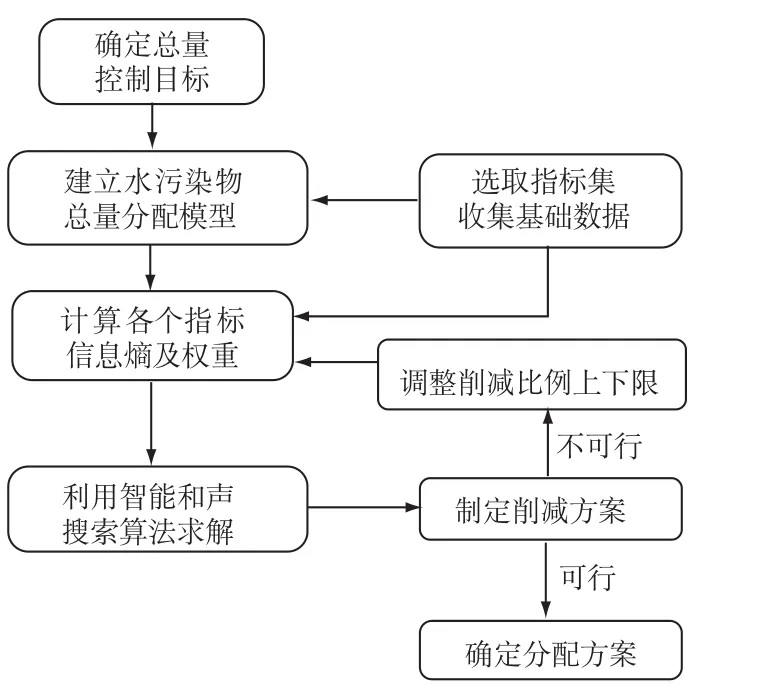
图1 基于最大加权信息熵的水污染物总量分配技术路线Fig.1 Technical route of the total amount allocation of water pollutant based on maximum sum of weighted information entropy

4.2.2 基础数据及现状分析

依据典型性、可量化、易采集、消除人为因素的原则，本文以汉中市2010年各县区的人口、生产总值、水资源量、水环境容量这4项指标值和2010年各区域的COD的排放量为基础数据。这些基础数据均来自于《2010年汉中市统计年鉴》和《2010年汉中市环保局环境统计公报》，如表2所示。

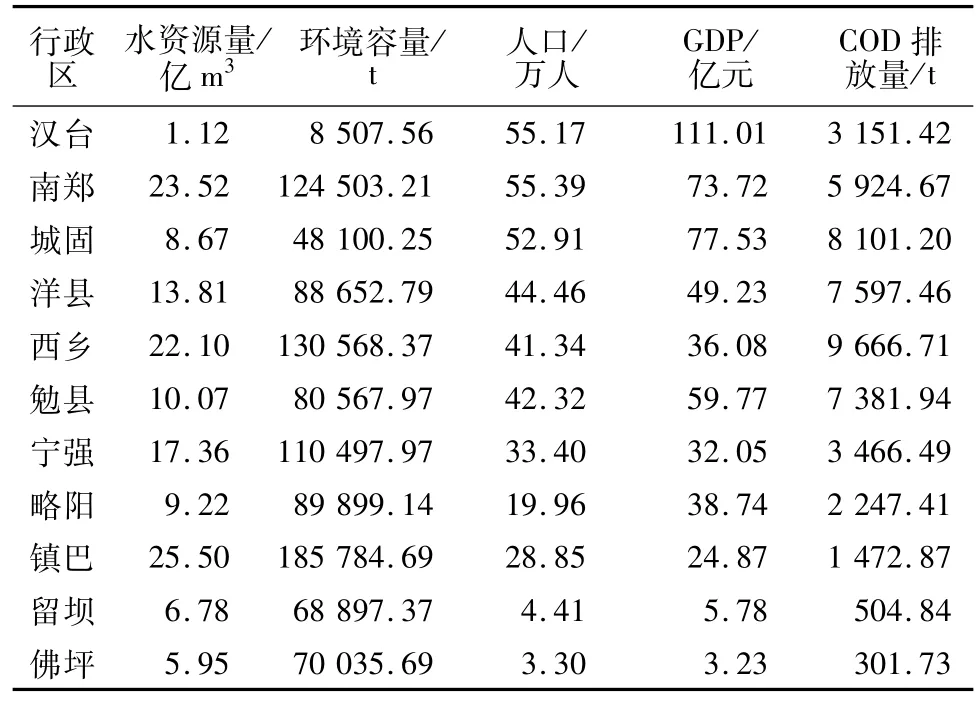
表2 汉中市2010年社会经济环境指标Table 2 Indexes of society，econom y and environment in Hanzhong in 2010

根据加权信息熵的分配模型，计算出2010年各项指标单位负荷污染物量的信息熵及加权信息熵总和，计算结果如表3所示。

表3 汉中市2010年各指标信息熵及信息熵加权和Table 3 The inform ation entropy and the sum of weighted information entropy of indexes in Hanzhong in 2010

从上述结果可以看出水资源量和环境容量这2项指标所负荷的污染物量的信息熵明显偏低，说明各区域间对水资源和水环境容量的利用水平差异较大，排污量与水资源量和环境容量不协调，汉台区属于中心城区，水资源量最少，COD排放量却明显超过水资源丰富和环境容量大的佛坪、留坝、宁强等山区。人口和GDP这2项指标的信息熵比较高，说明各地区污染物的排放量与人口数量和经济发展状况基本适应。

4.3 优化分配方案

按照上述模型以各区域削减比例为决策变量，根据决策变量的约束条件，采用3种分配方案，按照基于最大加权信息熵的总量分配模型，利用现代智能优化算法和声搜索算法求解，得到如表4所示的信息熵优化结果和表5所示的具体分配方案。

4.4 结果分析

从表4的信息熵优化结果来看，人口和生产总值2个指标下的单位指标污染物负荷基本平衡，因此随着削减比例的增大，这2项指标的信息熵值变化很小，说明这2项指标下的COD排放量分布较为均匀。表5的结果表明随着相对于现状的削减比例逐渐增大，各区域可优化的比例增加，各指标的信息熵值也随之增加，说明公平性也随之增强。表5中的结果表明：汉台区、城固和勉县3个行政区的削减比例较大，属于重点削减区域。结合表2可以看出汉台区、城固和勉县3个县区的水资源量和环境容量占到全市总量的约13%，水污染物COD的排放量却占到全市总量的37%，尤其是汉台区的水资源量仅仅占0.7%，COD排放量却占到6%，说明这些地区的单位水资源和环境容量指标的污染物负荷偏大，应该加大削减力度，另外南郑和洋县拥有全市10%的水资源，却占有全市22%的COD排放量，也应适当加大削减力度。3种削减方案中，方案3能够完成在2010年总量（49 816 t）的基础上完成削减任务，方案2在3个重点削减区域的削减比例全部取上限值时也能顺利完成。

表4 基于最大加权信息熵模型的优化结果Table 4 Optim ized results based on themodel ofmaximum sum of weighted information entropy

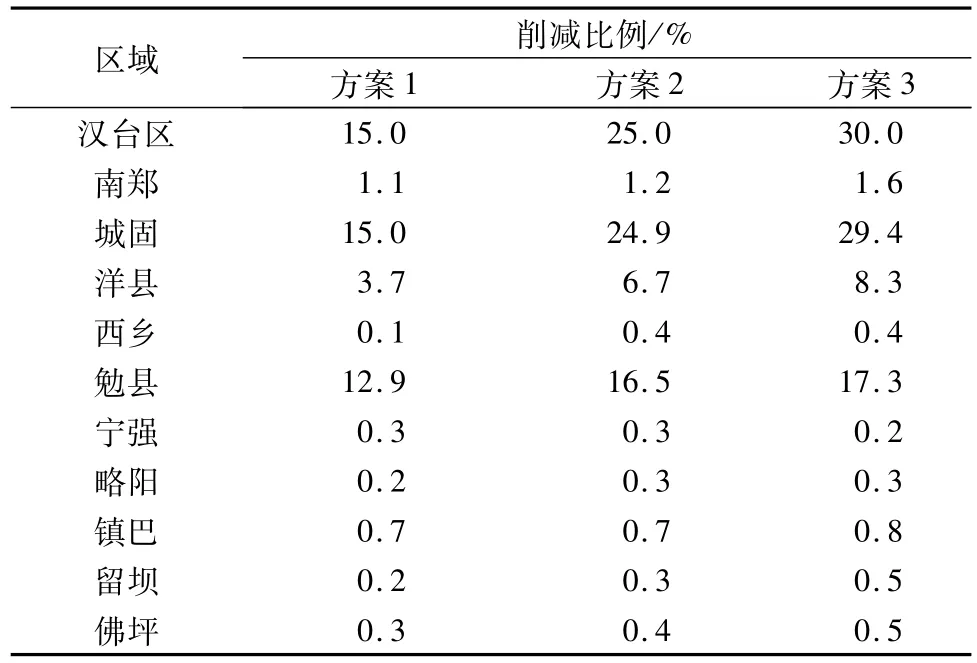
表5 基于最大加权信息熵模型的3种方案削减比例Table 5 Rate of em ission reduction in three schemes based on themodel ofmaximum sum of weighted information entropy

5 结 语

水污染物的公平分配方法目前仍然是个有争议的研究热点问题，分配方式也有很多种。实现区域的公平分配必须考虑区域间的自然和经济发展差异状况，必须将与COD排放密切相关的每个因素量化为衡量公平的指标，杜绝任何影响分配结果的主观因素才能最大程度地实现公平分配。本文利用信息熵概念，建立各个指标的信息熵最大加权和目标函数，研究了汉江流域汉中段各区域的COD排放总量优化分配问题，并利用了现代新型智能算法和声搜索算法，经过多次试验，最终给出了汉中地区水污染物COD的分配方案。结果显示汉台区、城固和勉县3个行政区的单位水资源和环境容量2个指标下COD负荷偏高，属于重点削减区域，该情况与实际情况相符。优化分配后进一步减小了各区域COD排放量与其本身的自然经济状况之间的差异，更大程度地体现了公平性，为汉江水源地汉中的水质保护和COD总量控制提供了理论参考。

［1］曹瑞钰，顾国维.水环境治理工程费用优化模型［J］.同济大学学报，1997，25（5）：548－552.（CAO Rui-yu，GU Guo-wei.Optimum Cost Model for Environmental Water Treatment Engineering［J］.Journal of Tongji University，1997，25（5）：548－552.（in Chinese））

［2］王有乐.区域水污染控制多目标组合规划模型研究［J］.环境科学学报，2002，22（1）：107－110.（WANG You-le.Study on the Multi-purpose Combination Planning Model of RegionalWater Pollution Control［J］.Acta Scientiae Circumstantiae，2002，22（1）：107－110.（in Chinese））

［3］李如忠，汪家权，钱家忠.区域水污染负荷分配的Delphi-AHP法［J］.哈尔滨工业大学学报，2005，37（1）：84－88.（LI Ru-zhong，WANG Jia-quan，QIAN Jiazhong.RegionalWater Pollution Load Distribution of Delphi-AHP Method［J］.Journal of Harbin Institute of Technology University，2005，37（1）：84－88.（in Chinese））

［4］盛 虎，李 娜，郭怀成.流域容量总量分配及排污交易潜力分析［J］.环境科学学报，2010，（3）：655－662.（SHENG Hu，LINa，GUO Huai-cheng.Analysis of Total Amount Allocation and Emission Trading Potential in a Watershed［J］.Acta Scientiae Circumstantiae，2010，（3）：655－662.（in Chinese））

［5］黄耀英，郑 宏，田 斌.信息熵理论在岩体结构加速流变破坏分析中的应用研究［J］.长江科学院院报，2011，（8）：50－54.（HUANG Yao-ying，ZHENG Hong，TIAN Bin.Application of Information EntropyTheory to the Failure Analysis of Accelerated Rheology of Rock Structure［J］.Journal of Yangtze River Scientific Research Institute，2011，（8）：50－54.（in Chinese））

［6］张 妍，杨志峰，何孟常，等.基于信息熵的城市生态系统演化分析［J］.环境科学学报，2005，25（8）：1127－1134.（ZHANG Yan，YANG Zhi-feng，HE Meng-chang，etal.Analyses on Evolution of Urban Complex Ecosystem Based on Information Entropy［J］.Acta Scientiae Circumstantiae，2005，25（8）：1127－1134.（in Chinese））

［7］刘 燕，胡安焱，邓亚芝.基于信息熵的用水系统结构演化研究［J］.西北农林科技大学学报（自然科学版），2006，34（6）：141－144.（LIU Yan，HU An-yan，DENG Ya-zhi.Study on the Evolution ofWater Resource Structure Based on Information Entropy［J］.Journal of Northwest Sci-Tech University of Agriculture and Forestry（Natural Science Edition），2006，34（6）：141－144.（in Chinese））

［8］朱方霞，陈华友.确定区间数决策矩阵属性权重的方法——熵值法［J］.安徽大学学报（自然科学版），2005，30（5）：4－6.（ZHU Fang-xia，CHEN Hua-you.A Method of Entropy for Obtaining the Attribute Weights of Interval Numbers Decision-making Matrix［J］.Journal of Anhui University（Natural Science Edition），2005，30（5）：4－6.（in Chinese））

［9］常福宣，陈 进，张洲英.汉江中下游水资源风险分析与对策研究［J］.长江科学院院报，2013，（7）：11－15.（CHANG Fu-xuan，CHEN Jin，ZHANG Zhou-ying.Water Supply Risk in the Middle and Lower Reaches of Hanjiang River and Its Countermeasures［J］.Journal of Yangtze River Scientific Research Institute，2013，（7）：11－15.（in Chinese） ）

（编辑：赵卫兵）

Total Amount Allocation of W ater Pollutant Based on M odel of M aximum W eighted Information Entropy

LIU Jie
（School of Mathematics and Computer Science，Shaanxi University of Technology，Hanzhong 723000，China）

Information entropy is applied to establish a fair and efficient allocation system of totalwater pollutant between areas.With COD（Chemical Oxygen Demand）in Hanzhong city which is the birthplace of Hanjiang river as an example，we select some indexes that are closely related with the emission of COD and quantified them in consideration of the natural and economic differences between areas.Then the index weights are decided by entropy evaluation method.The goal programmingmodel is thus established for themaximal sum ofweighted information entropy.Finally，the intelligent Harmony Search Algorithm is used to solve this problem to obtain fairer cuts.The results show that thismethod could quantify various fair standards and get optimized and feasible allocation schemes.

water pollutant；fair allocation；COD；total amount allocation；information entropy；maximum weighted；Harmony Search Algorithm；Hanzhong in Shaanxi Province

X522

A

1001－5485（2015）01－0016－05

10.3969/j.issn.1001－5485.2015.01.004

2013－10－25；

2013－11－18

陕西省教育厅科研计划项目自然科学专项（2013JK1161）

刘 杰（1982－），女，陕西汉中人，讲师，硕士，主要研究智能算法及应用，（电话）15029764288（电子信箱）slg＿liujie＠126.com。