频率测量模式在薄板分层损伤探测中的应用*

2015-06-09成鑫磊肖光宏Kennedy成培江

振动、测试与诊断 2015年3期

关键词：合板薄板固有频率

成鑫磊，肖光宏， Kennedy D, 成培江

(1.重庆交通大学土木建筑学院重庆，400074) (2.卡迪夫大学工程学院英国，卡迪夫,CF24 3AA)

(3.后勤工程学院土木工程系重庆，401311)

频率测量模式在薄板分层损伤探测中的应用*

成鑫磊1,2，肖光宏1， Kennedy D2, 成培江3

(1.重庆交通大学土木建筑学院重庆，400074) (2.卡迪夫大学工程学院英国，卡迪夫,CF24 3AA)

(3.后勤工程学院土木工程系重庆，401311)

分层损伤是复合材料的主要破坏形式之一，该类损伤发展到一定程度时，不仅会导致结构承载力降低，更有可能因结构失效而引起灾难性破坏。针对此问题，基于固有频率易于测量、测量精度高的特点，将正交化后的固有频率变化量应用于含有分层损伤的复合材料薄板结构中，提出了一种新型反向确定结构损伤位置的理论方法。该方法应用于无损检测中，作为结构损伤定量检测的前期工作，在定量无损检测之前，可以一定范围内准确地预测分层损伤的位置，提高检测效率。利用该方法对复合材料薄板分层损伤位置进行了探测，并与试验结果进行了对比分析。结果表明，该方法具有较好的精确性，实施步骤简单、可靠，并具有一定的抗噪性。

固有频率；薄板结构；分层损伤；位置预测

引言

当今，碳纤维增强树脂基复合材料(carbon fibre reinforled polymer,简称CFRP)越来越多地应用于航空、航天结构中，其轻质、高强的特点满足航空、航天领域轻质量化设计的要求。随着对复合材料的不断深入研发和试验应用，民用飞机结构中，包括作为主要承力构件的机翼和机身部分，越来越多地使用复合材料。应用碳纤维复合材料的翼肋、机身腹板通常假设为薄板结构[1]，相比于传统金属材料，CFRP具有较高的比刚度和良好的抗疲劳特性，可以满足结构特定的加载要求。但是这种材料在制造或使用过程中，容易在内部产生不易察觉的分层损伤，并且随着分层损伤的扩大化，导致材料的结构强度和刚度大幅度下降，同时造成结构抗失稳能力急剧降低，影响航空、航天器中复合材料薄板结构的使用性和安全性。目前，对复合材料进行无损检测的技术方法主要有超声检测法、微波检测法、涡流法和液体渗透检测法等多种技术。其中，超声检测，如超声扫描成像技术、基于Lamb波的检测方法等，是目前应用在复合材料中最为广泛的定量无损检测技术[2]。分层损伤导致结构的整体刚度降低，结构固有频率的大小也会因整体刚度的降低而减小[3-4]。固有频率的降低程度与分层损伤的严重程度及所处位置相关，因此，基于固有频率易于测量、测量精度高的特点，通过研究固有频率的变化，反向确定结构损伤位置，在薄板结构实施定量无损检测之前，快速、高效地确定结构分层损伤位置，作为结构损伤定量检测的前期工作，可以加快检测工作，提高检测效率，降低维护成本。目前，利用测量固有频率对框架梁、柱损伤进行分析，可以有效预测结构的损伤位置[5-7]。由于利用固有频率实现薄板结构的分层损伤预测还处于起步阶段，理论预测方法较为复杂[8-9]，因此，对复合材料薄板结构，提出了一种利用正交化后的固有频率变化量，反向确定结构分层损伤位置的理论方法。该方法应用于无损探测中，可以在一定范围内准确地预测分层损伤的位置，对快速确定机翼等薄板结构中分层损伤位置具有一定的意义。

在薄板结构的自由振动分析中，精确刚度阵法在横向使用动力刚度阵法，在纵向假设以正弦波形振动。与有限单元法及条分法相比，该方法不仅可以避免结构离散产生的误差，同时可以将结构视为无限自由度体系，利用振动微分方程导出的动力刚度矩阵集成到整体动力刚度矩阵中，将结构的自由振动分析转化为求解具有超越方程的动力刚度矩阵，从而得到所需的自振频率[10]。对于此类非线性超越特征值问题，Wittrick-Williams算法能够可靠、高效地加以解决，该算法可以获得任意阶数、任意精度的特征值。基于动力刚度阵法和Wittrick-Williams算法，英国卡迪夫大学研发的薄板结构设计和优化电脑程序VICONOPT[11]作为薄板结构与受损结构建模的工具，并获得固有频率。利用薄板结构与受损结构中的频率变化，反向确定分层损伤位置的理论算法将通过自编程序由Matlab软件实现。

1 薄板结构分层损伤模型及机理

固有频率的降低程度与分层损伤的严重程度及所处位置相关。基于频率测量模式的分层损伤探测方法的原理为：通过研究固有频率变化量，引入影响分层损伤严重程度因素及影响分层损伤位置因素的概念，可以预测分层损伤位置。

图1所示长为l、宽为b、厚为h,x方向两长边自由、y方向两短边简支的薄板结构，y方向设置中心对称，距左侧支座距离为B，存在长为d、宽为β、厚度无穷小的分层损伤，同时分层损伤形心沿x方向距边缘距离为D。从图1可以看出，在分层损伤的建模过程中，分层损伤由所处坐标轴3个方向的位置(D，B和hd)、分层损伤自身长度(d)与宽度(β)5个参数构成。

由于VICONOPT建模的输入要求，薄板结构沿x方向的材料、截面性质及受力状态需保持恒定不变，使得复合材料薄板结构中最常见的内部矩形

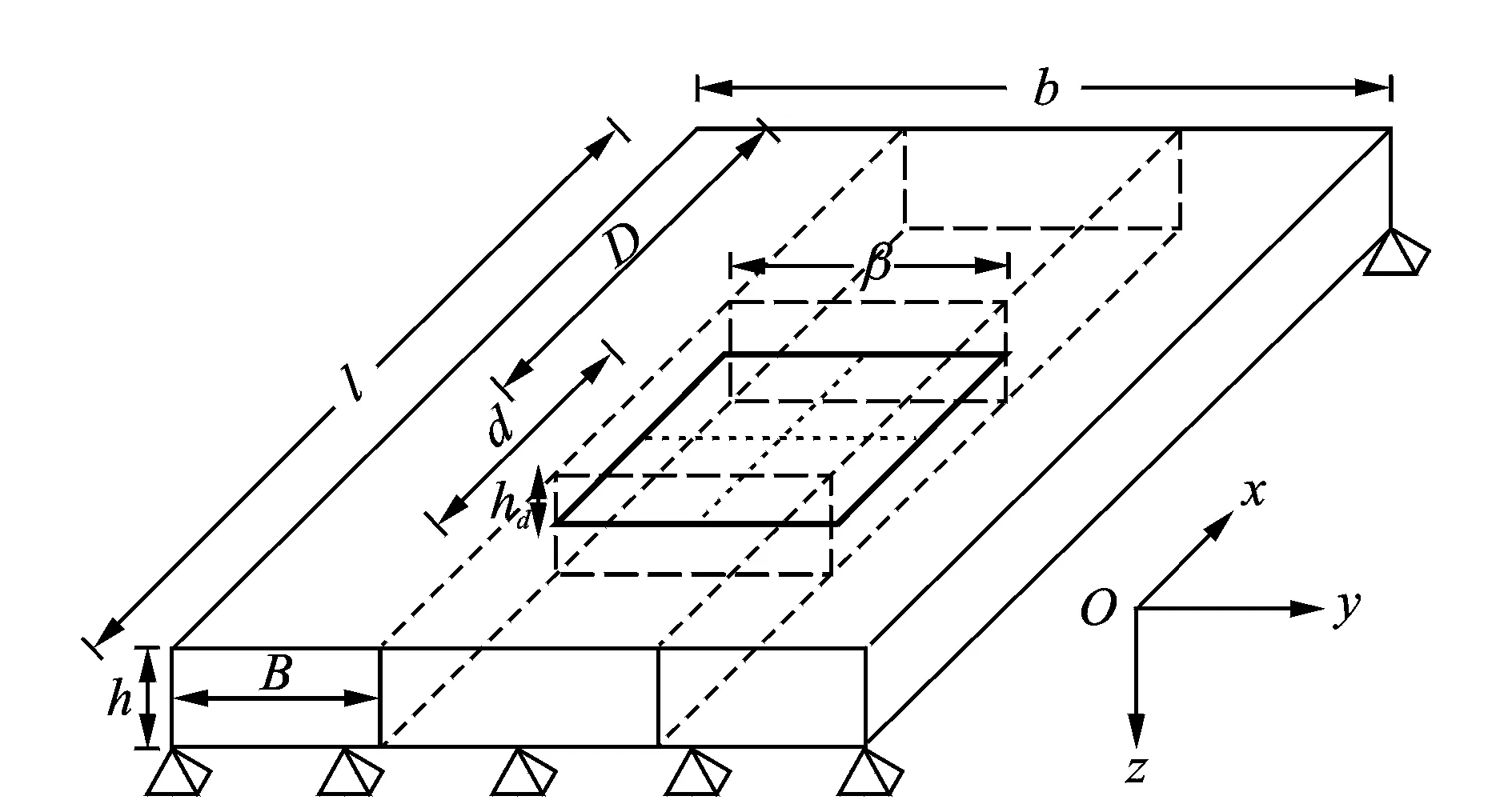
图1 薄板结构中分层损伤模型的位置与尺寸Fig.1 Position and dimension of delamination model in plate structure

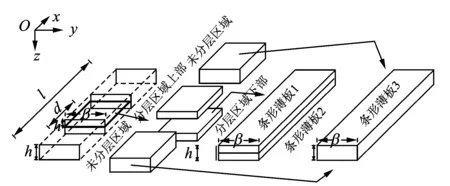
图2 分层损伤模型中的涂敷法Fig.2 Sketch of using smearing method on delamination model

分层损伤无法直接建立模型。Damghani等[4]基于软件性质，提出涂敷法将薄板结构中含有分层损伤的条形区域划分为3个部分，即分层区域上下部与未分层区域,如图2所示。通过分析薄板结构中分层区域与未分层区域对结构势能的影响，将结构中含有分层损伤的条形区域的3个部分，分别转化为处于同样位置的3个不同的条形薄板。

记μ=d/l，ξ=D/l，得到结构x方向薄板含有分层损伤的条形区域的等效刚度矩阵，记为

(1)

其中：K为条形区域未分层部分的单位长度刚度矩阵；k为条形区域处分层部分的单位长度刚度矩阵；m为0到∞的正整数，是x方向出现半波的个数。

从式(1)可以看出，增加分层损伤长度d=μl会导致结构等效刚度矩阵降低，从而导致结构固有频率值降低。此外，宽度β作为分层损伤的另一个尺寸因素，其增长扩大亦造成结构等效刚度矩阵被削弱(将长宽旋转90°可以得到宽度方向的公式(1))，同样会导致结构固有频率值降低。分层损伤深度hd将截面划分为二，导致截面相对高度h降低，由薄板抗弯刚度公式D=Eh3/12(1-υ2)可知，分层损伤使得结构刚度下降，导致结构固有频率值降低。

2 薄板结构分层损伤探测的原理

在探测分层损伤的过程中，为简化分析，假设分层损伤沿x方向成条形完全覆盖，因此在探测分析中将不考虑分层损伤长度及在x方向位置2个参数的影响。由于结构刚度会随分层损伤宽度的增大而降低，当分层损伤宽度β增大到一定范围时，会导致损伤区域的振动模式与薄板结构的振动模型不再一致(称为局部振动模式)，从而使得薄板结构损伤区域的固有频率产生大幅度下降[3-4]；因此，分层损伤的宽度被定义为影响分层损伤严重程度的因素。当分层损伤的位置沿z方向从薄板平面中心hd=h/2向边缘移动时，结构会因为分层损伤在z方向过于接近表面，造成损伤区域屈曲分层，使得薄板结构损伤区域的固有频率产生大幅度下降；因此，在z方向移动分层损伤的位置同样被认为是影响分层损伤严重程度的因素。在分层损伤模型的所有参数中，只有分层损伤在y方向的移动是由于不同位置的分层损伤而引起固有频率在线性范围变化的因素，并不会导致损伤区域进入局部振动模式，产生大幅度下降；所以，将分层损伤在y方向的移动定义为唯一影响分层损伤位置的因素。

固有频率受分层损伤严重程度的影响，其下降趋势为：首先是小幅度的线性降低，然后超过某一临界值后以抛物线形式急剧下降[3-4]。参考Damghani等[3]关于条形分层损伤的有限元模拟以及VICONOPT计算模型，笔者将考虑β=0.2B为触发损伤区域振动模式改变的临界值。当固有频率的下降仍处于线性范围内，由于损伤区域振动模式与薄板结构振动模式仍保持一致(称为整体振动模式)，此时通过模拟受损结构建立关于固有频率的损伤数据库，结合区间算术原理，结构真实分层损伤在y方向的位置可以被本方法探测到，然后再通过定量无损检测，确定损伤实际宽度β和z方向位置hd。尽管分层损伤区域进入局部振动模式时，本方法失效，然而使用本方法的目的是在分层损伤严重程度扩大化、引起严重的结构失效破坏之前，提前预警并快速、准确地将其位置探测出来，进行修复，以保证结构的安全性和使用性。

3 薄板结构分层损伤探测的方法

以图1中x方向两长边自由、y方向两短边简支、分层损伤沿x方向完全覆盖的薄板结构为例，假设结构在x方向以半波λ的正弦形式振动。在此边界条件下，探测计算会选取λ=l，l/2，l/3和l/4各自的前4个固有频率ωijo和ωij，分别由不含分层损伤的完好结构和含有分层损伤的受损结构计算所得，用于分层损伤位置的探测。薄板结构的固有频率变化量在探测计算理论中被定义为δij

(2)

(3)

其中：i为薄板结构x方向出现正弦半波的个数；j为y方向振动的模态数；s为分层损伤严重程度的函数，且与结构振动模态数不相关；fij(B/b)为分层损伤距y方向支座距离的无量纲函数。

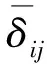
(4)

其中：分母同时对δij的下标i和j求平方和；分子为任意固有频率变化量δij。

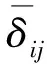
(5)

其中：-1.0 ≤Gij(B/b)≤1.0。

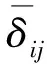
(6)

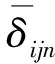
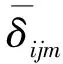
图3所示在b=100 mm的薄板结构中，处于y方向不同位置β=10 mm，hd=h/2的条形分层损伤与某受损结构某半波下4个实测固有频率形成的Gij(B/b)曲线图(考虑简支约束的对称性，因为(b-β)/2=45 mm，所以图中横轴数值B/b在此仅取至0.45)。

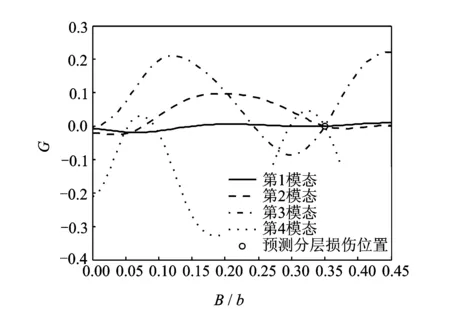
图3 不同位置的分层损伤形成的G曲线Fig.3 G curve for delamination at varying location

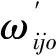
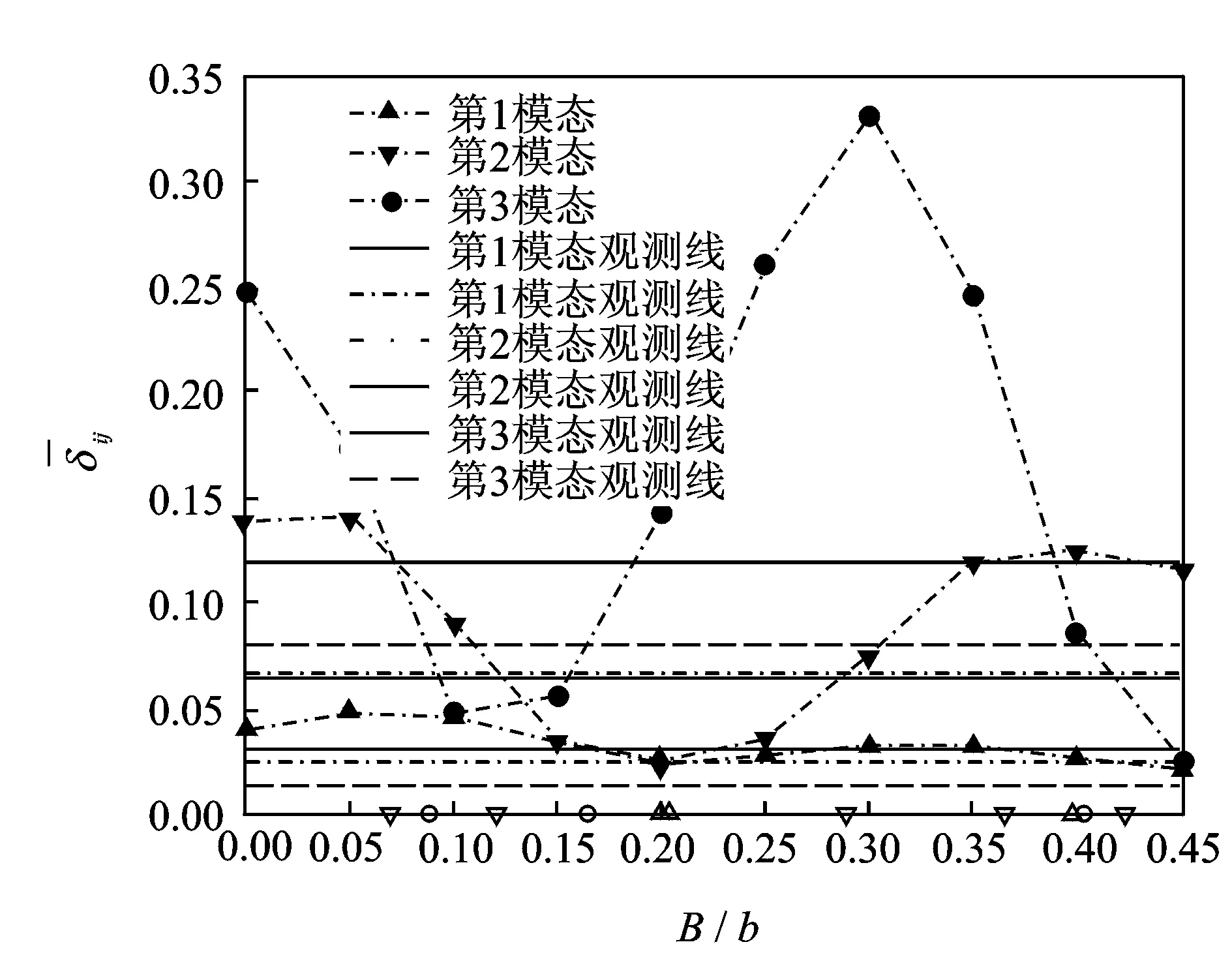
图4 结合3个半波下的与值的损伤位置预测Fig.4 Detection using and value combined 3 half-wavelength

4 探测方法试验验证

4.1 试验背景宏观描述

基于笔者以Matlab为平台的自编程序，利用文献[8]中的试验结果反向确定复合材料薄板结构中分层损伤的位置，以验证该方法的可靠性。文献[8]使用16层按 [0/0/90/90/0/0/90/90]s铺设的层合板进行自由振动试验，并完成对该结构的振动响应参数测量。该层合板长l=240 mm，宽b=180 mm，厚度h=2.08 mm。材料参数分别为：E1=125 GPa；E2=E3=8.5 GPa；G12=G13=4.5 GPa；G23=3.27 GPa；υ12=υ13=υ23=0.3；密度ρ=2 400 kg/m3。从图5可以看出该结构的边界条件：x方向两长边自由，y方向两短边简支约束。在层合板的第4层和第5层处，即hd=h/4处，预埋长d=36 mm、宽β=24 mm、厚度h=0.015 mm的矩形聚酯薄膜模拟分层损伤，分层损伤位置中心如图5所示。同时，该图也展示了面积为15 mm×25 mm、厚度h=0.3 mm的压电陶瓷片作为激振器贴在层合板上下表面处。图6所示为层合板上表面安装有一个加速度计及发出激励信号、记录响应信号的过程。该试验的激励信号由波形发生器TTi TGA1241产生，功率放大器与电荷放大器分别用来增强信号发生器与变换器的信号，试验的激励信号及响应信号均由FFT的频谱分析仪(B&K 3550)进行记录和分析。为消除测量误差的影响，Wei等[8]将试验重复8次，取测量平均值作为最终试验数据。

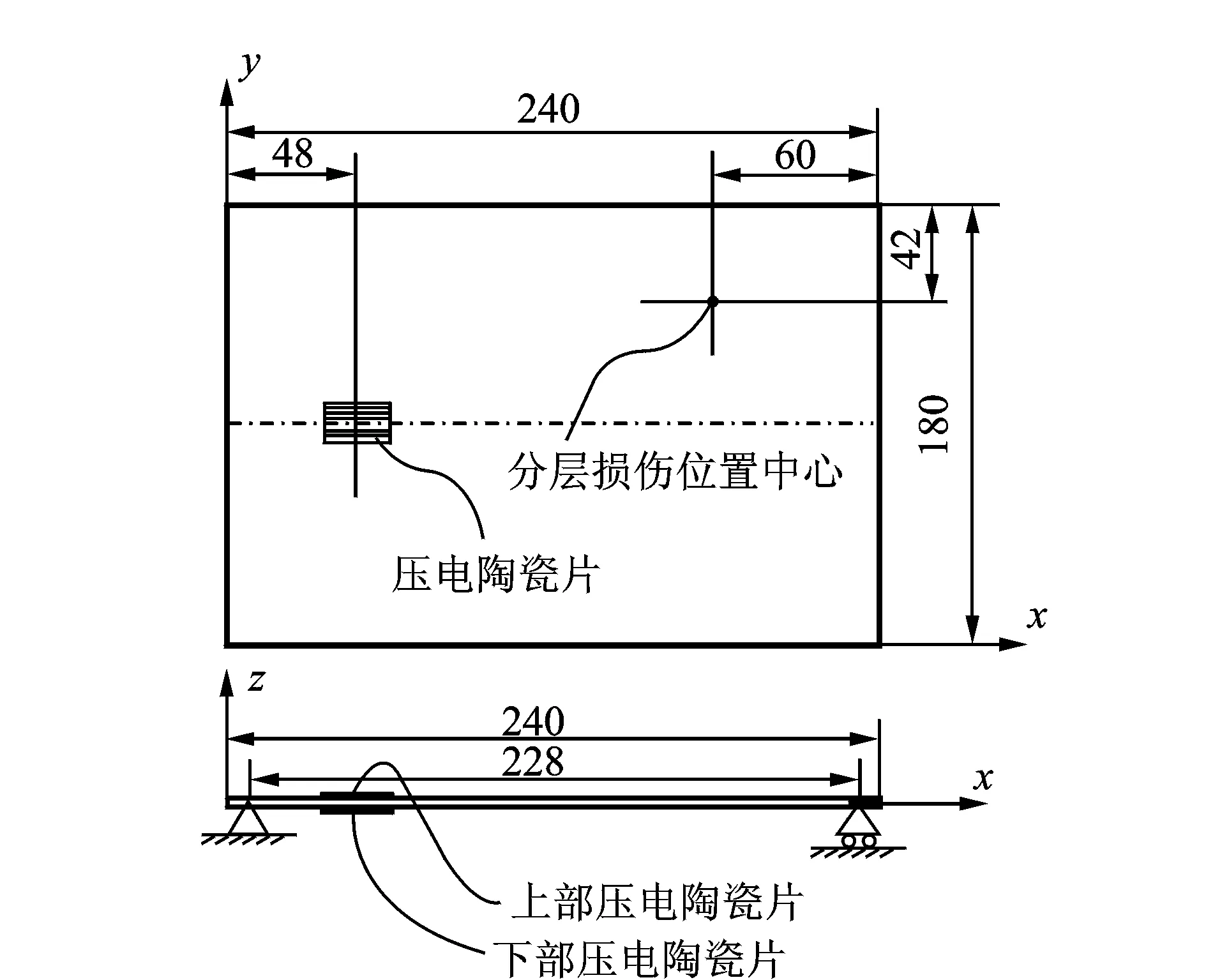
图5 层合板试件及压电陶瓷片位置(单位：mm)Fig.5 Sample dimension and the locations of actuators(unit:mm)

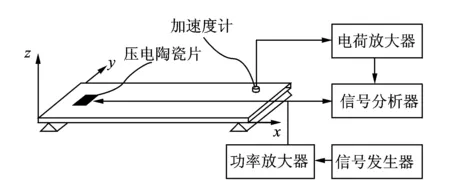
图6 层合板振动试验的激励及响应过程Fig.6 The experimental set-up for response of the composite plates

4.2 探测方法试验验证及误差分析

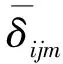
从图7、图8可以看出，区域[24.31, 33.00]是基于各模态下所预测出的最有可能的实际分层损伤位置，即距支座24.31～33.00 mm处存在宽度β=25 mm，hd=h/2的条形分层损伤。Wei等[8]试验中，β=24 mm，hd=h/4的真实分层损伤距离支座30 mm处，两者对比表明该方法探测的损伤区域结果具有一定的可靠性。然后沿y方向对薄板的[24.31, 33.00]所处的条形区域进行定量人工无损检测，再确定真实试件中的分层损伤位置和程度。

表1 复合材料层合板向自由振动分析结果

Tab.1 Free vibration analysis results of a healthy laminate

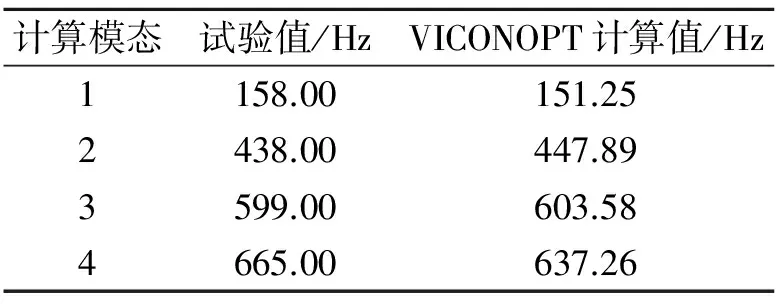
计算模态试验值/HzVICONOPT计算值/Hz1158．00151．252438．00447．893599．00603．584665．00637．26

表2 含有分层损伤的复合材料层合板向自由振动分析结果

Tab.2 Free vibration analysis 2 results for a delaminated laminate

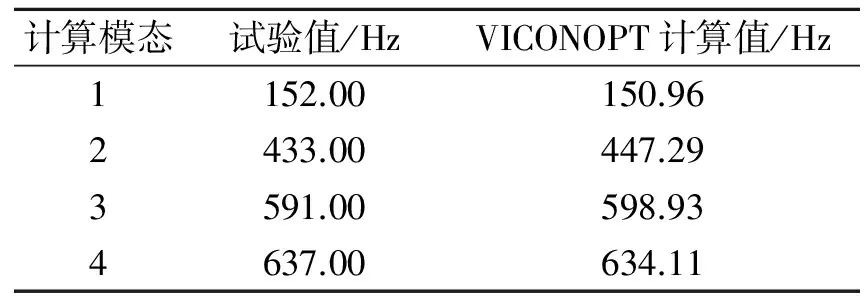
计算模态试验值/HzVICONOPT计算值/Hz1152．00150．962433．00447．293591．00598．934637．00634．11

表3 各模态下所预测的分层损伤位置

Tab.3 Results of the predicted delamination location in plate

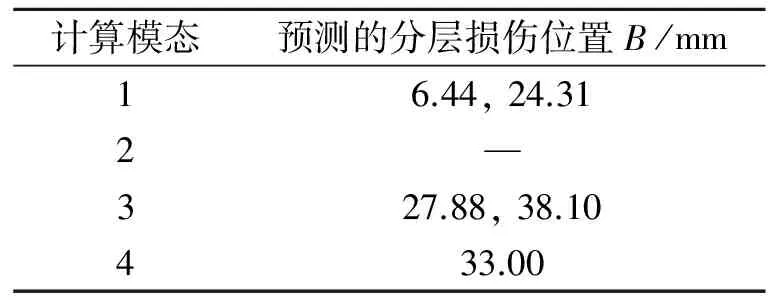
计算模态预测的分层损伤位置B/mm16．44，24．312—327．88，38．10433．00

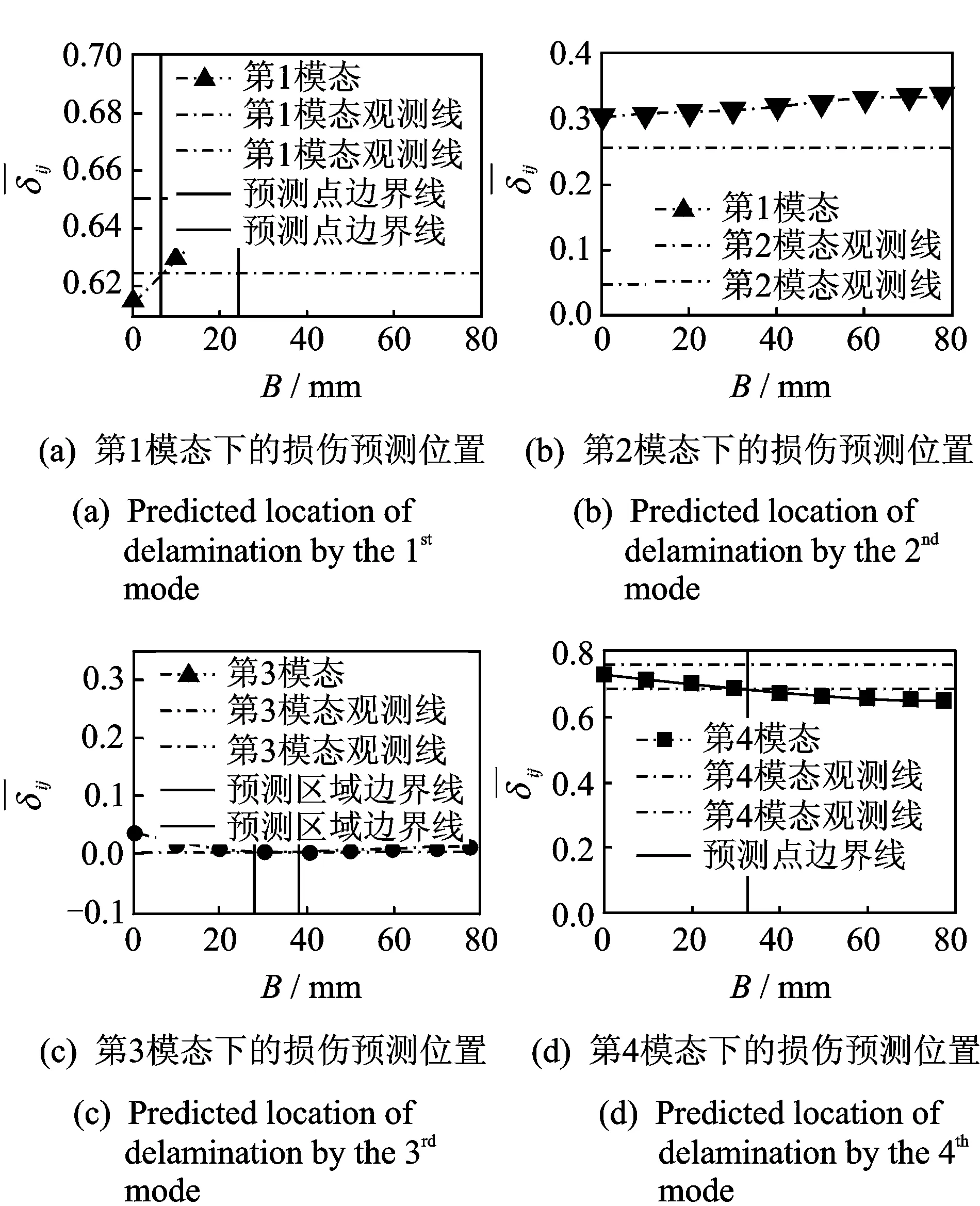
图7 各模态下可能的分层损伤的位置Fig.7 Predicted delamination location by each mode

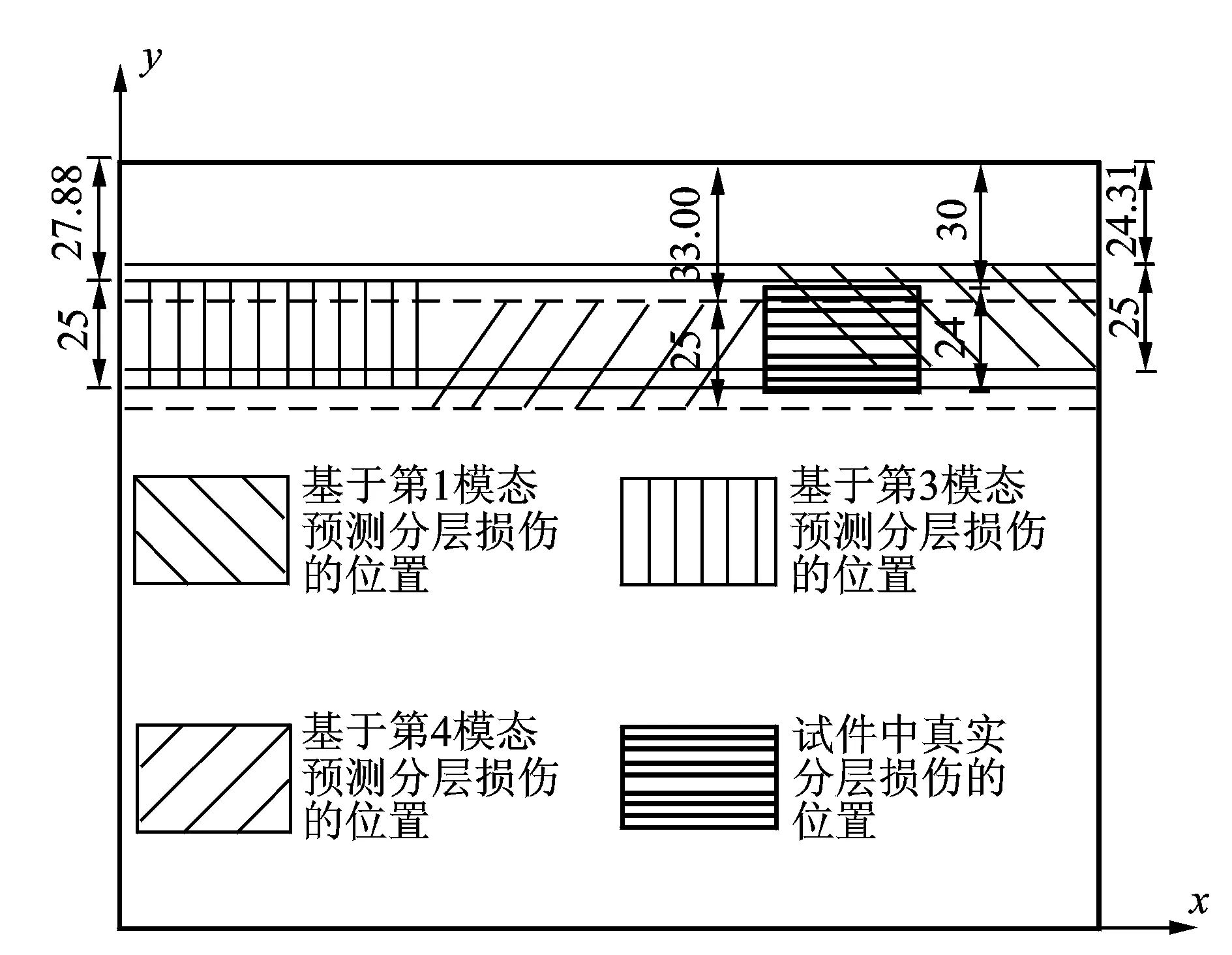
图8 各模态下所预测的分层损伤位置及真实分层损伤位置(单位：mm)Fig.8 Predicted delamination location by each mode and actual delamination location in experiment (unit: mm)

5 结束语

基于固有频率测量精度高、测量方法简单的特点，提出了一种新型的、利用正交化的固有频率变化量，反向确定复合材料薄板结构中分层损伤位置的无损探测方法。通过研究结构固有频率变化趋势，引入影响分层损伤严重程度因素及影响分层损伤位置因素的概念。在此基础上，利用复合材料层合板试验数据建模，通过对比该方法所预测的分层损伤位置与真实试件中分层损伤位置，分析预测结果的精确性，验证了该方法的可靠性，且计算过程快速、简单。试验结果表明，不同宽度β、不同深度hd的分层损伤的位置可以在同一模型中被探测出来，一定程度上扩大了分层损伤的探测范围，简化了探测工作。基于频率测量模式的分层损伤探测方法可以作为薄板结构分层损伤无损探测的理论基础，对快速确定复合材料薄板结构中分层损伤位置具有一定的意义。

[1] 赵群. 复合材料翼面结构布局优化设计方法研究[D]. 南京: 南京航空航天大学,2010.

[2] 裘进浩，张超，季宏丽，等. 基于激光激励技术的结构损伤成像[J]. 振动、测试与诊断,2014, 34(4): 603-609.

Qiu Jinhao,Zhang Chao, Ji Hongli, et al. Damage imaging for plate structures based on laser excitation [J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(4): 603-609. (in Chinese)

[3] Damghani M, Kennedy D, Featherston C. Critical buckling of delaminated composite plates using exact stiffness analysis [J]. Computers and Structures, 2011, 89(13-14): 1286-1294.

[4] Damghani M, Kennedy D, Featherston C. Global buckling of composite plates containing rectangular delaminations using exact stiffness analysis and smearing method [J]. Computers and Structures, 2014, 134: 32-47.

[5] Labib A, Kennedy D, Featherston C. Free vibration analysis of beams and frames with multiple cracks for damage detection [J]. Journal of Sound and Vibration, 2014, 333(20): 4991-5003.

[6] Khan K, Maiti S K. Delamination detection in a laminated composite beam based on changes in natural frequencies [J]. Mechanisms and Machine Science, 2014, 23(2): 519-533.

[7] 杨智春，党晓娟，王乐，等. 复合材料结构损伤联合定位法试验研[J]. 振动、测试与诊断,2010, 30(2): 115-118.

Yang Zhichun, Dang Xiaojuan, Wang Le, et al. Experimental investigation on a combined damage localization method for composite beams and plates [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 115-118. (in Chinese)

[8] Wei Z, Yam L H, Cheng L. Detection of internal delamination in multi-layer composites using wavelet packets combined with modal parameter analysis [J]. Composite Structures, 2004, 64(3-4): 377-387.

[9] Yang Zhibo, Chen Xuefeng, Yu Jie, et al. A damage identification approach for plate structures based on frequency measurements [J]. Nondestructive Testing and Evaluation, 2013, 28(4): 321-341.

[10]Wittrick W H, Williams F W. A general algorithm for computing natural frequencies of elastic structures [J]. Quarterly Journal of Mechanics and Applied Mathematics, 1971, 24(3): 263-284.

[11]Kennedy D, Williams F W, Anderson S. Buckling and vibration analysis of laminated panels using VICONOPT [J]. Journal of Aerospace Engineering, 1994, 7(3): 245-262.