基于电磁感应原理的薄壁件铣削振动抑制*

2015-06-09杨毅青龚继文

振动、测试与诊断 2015年3期

关键词：阻尼力电磁感应阻尼器

杨毅青，龚继文

(北京航空航天大学机械工程及自动化学院北京，100191)

基于电磁感应原理的薄壁件铣削振动抑制*

杨毅青，龚继文

(北京航空航天大学机械工程及自动化学院北京，100191)

航空结构中的薄壁件由于刚性差，在加工中容易发生变形、让刀等现象，对加工精度及表面质量构成严重影响。针对上述问题，基于电磁感应原理，笔者研究设计了适用于薄壁件的铣削加工减振装置，将工件的振动应用于磁感线切割，通过作用反力的产生来实现工件减振的目的，并推导了磁铁在铜管内运动时的电磁感应阻尼力，结果表明阻尼力与相对运动速度成线形关系，但方向相反。冲击实验表明，该减振装置能显著缩短薄壁件的振荡时间；颤振稳定域仿真表明，该装置可将薄壁零件的临界稳定切深从0.4 mm提高到5.1 mm。最后，结合切削实验对该装置的抑振效果进行验证。

薄壁件; 电磁感应; 铣削; 振动抑制

引言

整体薄壁零件在航空结构中大量存在。薄壁零件由于刚性差，加工中易发生变形、让刀等现象，使得加工精度及表面质量难以达到设计要求;因此,实现薄壁零件的高效高质切削是目前制造技术中所面临的难点问题。针对薄壁零件的数控铣削加工，国内外学者在工艺规划、工件装夹以及切削变形预测与控制等领域开展了大量研究。装夹变形是影响薄壁工件加工精度与表面质量的重要因素。以航空薄壁件为对象，秦国华等[1]提出了基于最小总余能原理的接触力求解技术，利用有限元法模拟了夹紧方案对工件变形的影响。Aoyama等[2]应用低温合金实现了对薄壁柔性零件的多点均匀支撑，有效抑制了工件加工中的弹性变形。Shamoto等[3]采用同步双面铣削技术加工薄壁件，通过使两工作主轴采取不同的转速以抑制颤振，加工精度及效率比传统的单面铣削方法提高3倍。Ratchev等[4]提出了考虑薄壁结构弹性的力-变形模型以预测加工误差，通过在加工之前对刀轨进行补偿和优化，表面误差明显减小。随着加工过程中工件材料的逐渐去除，工件本身的动力学特性在发生变化，从而改变了加工工艺系统的稳定性，薄壁零件尤其明显。不少学者对薄壁零件的铣削稳定性进行了研究[5-6]。上述工作为薄壁零件数控加工方案的解决提供了良好的借鉴，不过在目前的工程实际应用中，薄壁零件的加工仍然是难点。此外，通过采用主动与被动控制的方法来抑制切削加工中工艺系统的振动在众多文献中也有述及。Dohner等[7]设计了针对刀具的主动控制回路，将铣削加工的材料去除率提高了一个量级。结合压电驱动器，Rashid等[8]利用自适应控制策略对工装进行主动控制，提高了铣削加工的表面质量以及刀具寿命。主动控制采用反馈控制的原理，对系统进行连续的调节，具有较强的适应性，但成本高，实现复杂。Duncan和Rashid等[9-10]研究了单自由度被动阻尼器对铣削颤振的抑制。杨毅青等[11]设计了梁式结构的多重被动阻尼器以抑制车削颤振。被动阻尼器抑振频带较窄，需要结合一定的优化准则对阻尼器的结构参数进行优化后方能发挥其功用，而且被动阻尼器形式多样，增加了其结构建模以及参数优化工作的复杂程度。同时，切削过程的多变性也制约了被动阻尼器效能的发挥。

磁场环境下，闭合回路中的导体作切割磁力线运动时会产生作用反力，即阻尼力，而且阻尼力的大小随导体运动的速度而变化。基于此，笔者拟研究基于电磁感应原理的阻尼减振装置，通过将切削加工时工件的振动应用于磁感线切割，将工件振动的动能转化为势能，从而实现薄壁件铣削振动的抑制。本研究主要内容包括电磁感应阻尼器阻尼力建模、电磁感应阻尼器结构设计、阻尼器动态特性测试，并通过切削实验对电磁感应阻尼器的抑振效果进行验证。

1 电磁感应阻尼器原理分析

1.1 电磁感应原理

根据楞次定律，如果感应电流是由组成回路的导体作切割磁感线运动而产生，那么运动导体所受的磁场力(安培力)总是反抗(或阻碍)导体的运动。从能量守恒的角度，在磁场环境下导体的动能可转换成势能。基于该原理，设计电磁感应阻尼减振装置，将工件振动应用于磁感线切割，从而产生安培力并实现工件切削振动的抑制。

闭合回路的部分导体在均匀磁场中切割磁感线时产生感应电动势以及感应电流(见图1)

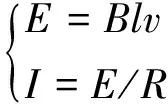
(1)

其中：B为磁感应强度；l为切割磁力线的导线长度；v为单元环与磁体相对运动速度；R为导体电阻，R=ρl/S；ρ为单位圆环金属材料的电阻率；S为单位圆环横截面积。

在磁场环境下，该导体受到安培力F的作用，其方向总是与产生感应电动势的运动方向相反

F=BIl

(2)

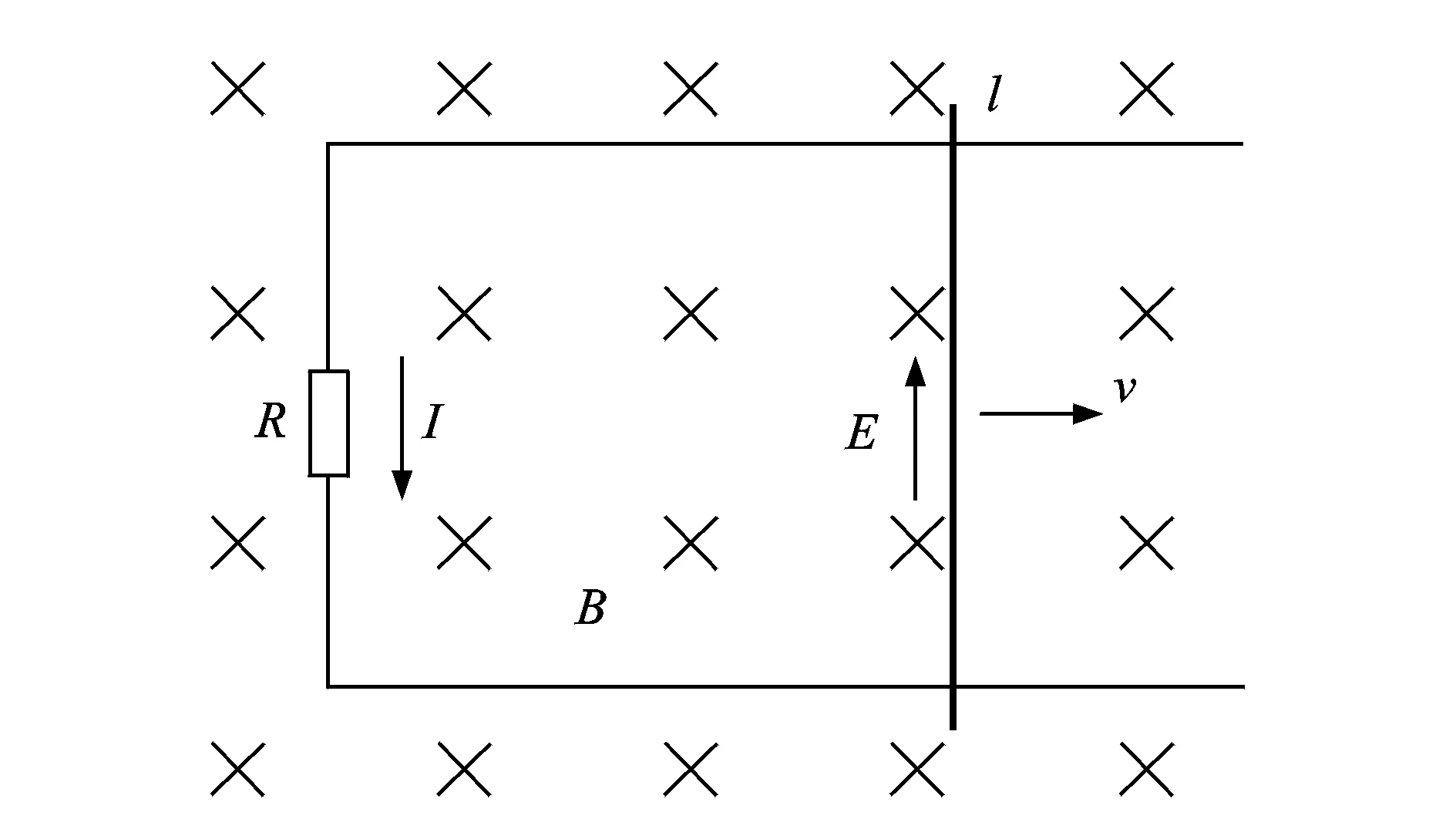
图1 电磁感应原理示意图Fig.1 Electromagnetic induction

结合式(1)和式(2)，可获得安培力F与导体运动速度v之间的关系表达式

(3)

1.2 电磁感应阻尼力

1.2.1 磁场强度空间分布函数推导

本研究的电磁感应阻尼装置设计拟采用扁圆柱形磁铁，该磁铁的磁场强度分布与圆电流产生的磁场相同，如图2所示。通常情况下，圆电流磁场可近似等效为磁偶极子模型[12]。据此，可得点P(rcosθ，rsinθ，z)处的磁感应强度B的矢量表达式[12-13]为

(4)

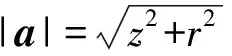
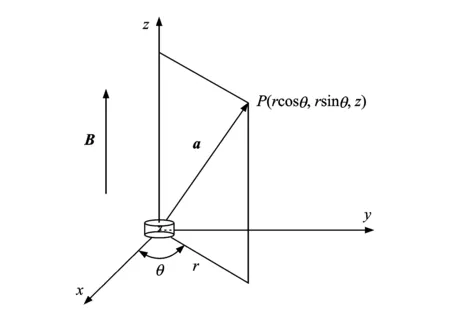
图2 空间任意点P处的磁场强度Fig.2 Magnetic field at Point P

扁圆柱形磁铁磁偶极矩m计算公式[12-13]如下

(5)

其中：r1为圆柱形磁铁半径；h为圆柱形磁铁高度；M0为磁铁的磁化强度，M0=Br/μ0，Br为剩磁。

结合式(4)、式(5)并将磁场强度B沿空间坐标系进行分解，获得x，y，z向的分量如下

(6)

1.2.2 圆环导体电磁感应阻尼力推导

当圆环导体沿z轴方向以速度v运动时(见图3)，仅切割磁偶极子水平方向上的磁感线分量。在磁偶极子作用下，同一水平面内且距z轴距离相等的所有点处的磁场强度相同，其水平分量Bxy为

(7)

根据式(1)～式(3)，圆环导体的阻尼力dF为

(8)

其中：r2为圆环半径；t为圆环厚度；dz为圆环高度；圆环长度l=2πr2；圆环截面积S=tdz。

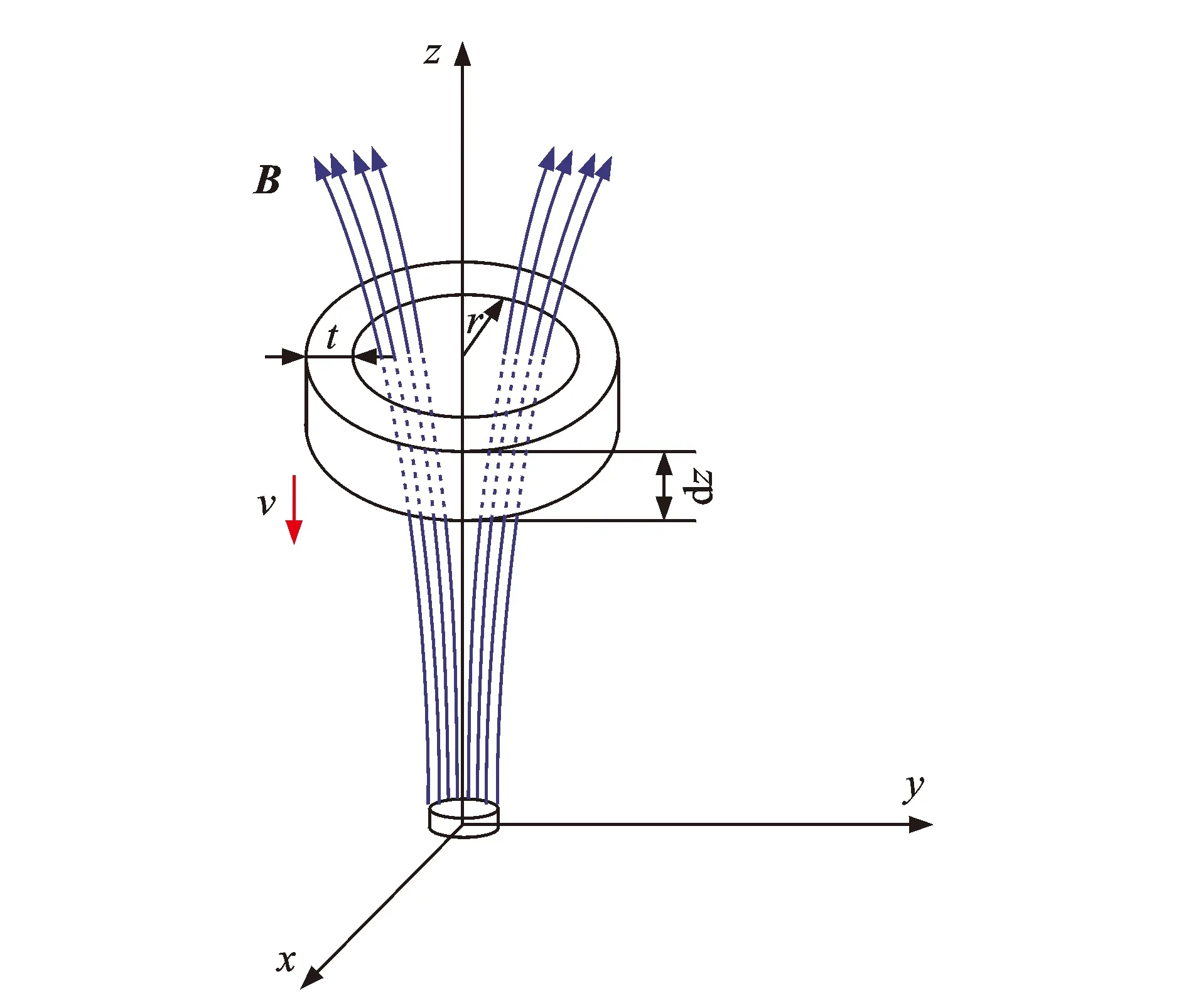
图3 圆环导体切割磁感线示意图Fig.3 Motion of a circular ring in the magnetic field

1.2.3 电磁感应阻尼力计算

近似情况下，铜管可视为由无数水平放置的单位圆环叠加而成。假设铜管长度为L，沿铜管方向对式(8)积分，获得铜管在电磁感应作用下所受到的阻尼合力为

F=Cv

(9)

其中：

C可定义为电磁感应阻尼系数，与磁铁和铜管的物理属性、位置等因素相关。由式(9)可得，电磁感应阻尼力F与圆环导体速度v之间成线性关系，但方向相反，效果与黏性阻尼类似。

2 电磁感应阻尼器结构设计及特性测试

2.1 电磁感应阻尼器结构设计

上述推导为电磁感应阻尼器设计的可行性提供了理论支撑。在此基础上，设计阻尼器结构如图4所示。工件与支撑固定在机床工作台的T型槽中，磁铁、空心铝棒、工件之间可通过强力胶水连接。铜管在支撑上的上下位置可通过螺母来调节。当薄壁工件受到切削力作用而发生振动时，磁铁跟随工件一起振动，使得铜管与磁场之间产生了切割磁感线的相对运动，从而产生了作用反力，有助于降低薄壁件振动的幅值。

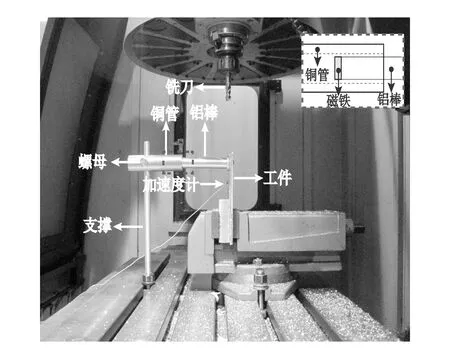
图4 电磁感应阻尼器结构方案设计Fig.4 Vibration suppression device design based on the electromagnetic induction

2.2 电磁感应阻尼器特性测试

在相同冲击下，分别测试薄壁件在使用与不使用阻尼器情况下的振动响应信号。测试结果如图5所示。在相同冲击力的情况下，安装阻尼器后工件的振动幅值能更加快速衰减。以90 N的瞬时冲击力为例(图5(a))，在不使用阻尼器的情况下，响应曲线进入稳态值±5%误差带所用时间为0.232 s；使用阻尼器后，缩短至0.089 s。在电磁感应作用下所产生的阻尼力起到了明显抑制工件振动的效果。

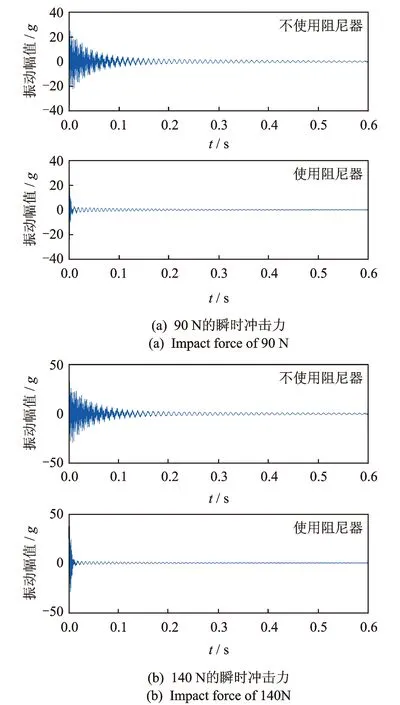
图5 使用与不使用阻尼器情况下薄壁件的振动信号Fig.5 Workpiece vibration comparison between using and without using the damper

3 实验验证

3.1 实验装置

切削实验在三轴铣床VMC0850B上开展，采用刀具为Sandvik圆柱螺旋立铣刀，直径φ=12 mm，刀齿数N=2。工件材料为铝合金2A12，尺寸为200 mm×160 mm×5 mm。实验过程中通过加速度计(Kistler 8776A50)及数据采集卡(NI 9233)获取工件的振动信号，数据采集软件为Cutpro V9.3。

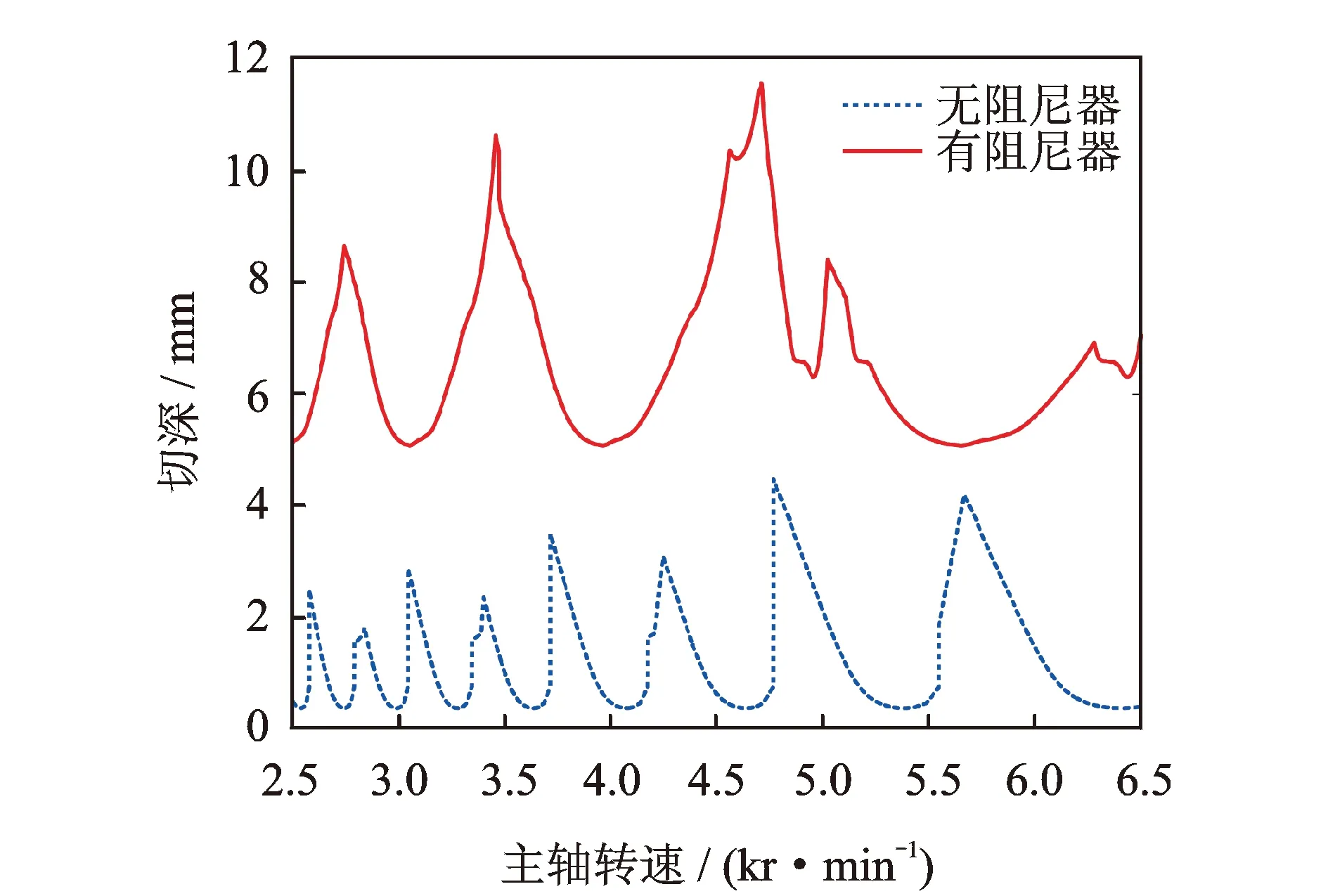
图6 阻尼器安装前后的薄壁工件颤振稳定域图对比Fig.6 Stability comparison between using and without using the damper

为合理选择切削参数，首先通过模态测试预测薄壁件的铣削颤振稳定域图。以切宽ae=2 mm，进给速度F=300 mm/min，顺铣为例，阻尼器安装前后的颤振稳定域图对比如图6所示。阻尼器安装之前，工件的颤振稳定域临界切深仅为0.4 mm；阻尼器安装之后，临界稳定切深增加到5.1 mm。仿真结果表明，阻尼器对薄壁件的切削稳定性有了明显提升。

3.2 切削实验结果

根据铣削稳定域图(见图6)，选取主轴转速S=3 kr/min为例。在不使用阻尼器的条件下，当切深为1 mm时，薄壁工件切削过程中采集到的振动信号如图7(a)所示。可见工件振动的幅值迅速增加且振动信号不平稳，瞬时加速度最大达到40g。对时域振动信号进行FFT变换后，以0～500 Hz区间为例，在刀齿切削频率fT=100 Hz以及倍频(100，300，400 Hz等)之外，频谱图显示在296,392,396 Hz等频率处还存在明显谐波分量，其中396 Hz的谐波分量(幅值为3.8)超过400 Hz频率(幅值为2.5)处，据此可判断切削过程发生颤振。保持切削参数不变，使用该减振装置后(见图7(b))，切削过程中工件振动的瞬时加速度下降至10g，且振动信号平稳。观察频谱，仅在刀齿切削频率及其倍频处存在明显谐波分量，表明切削过程处于稳态。

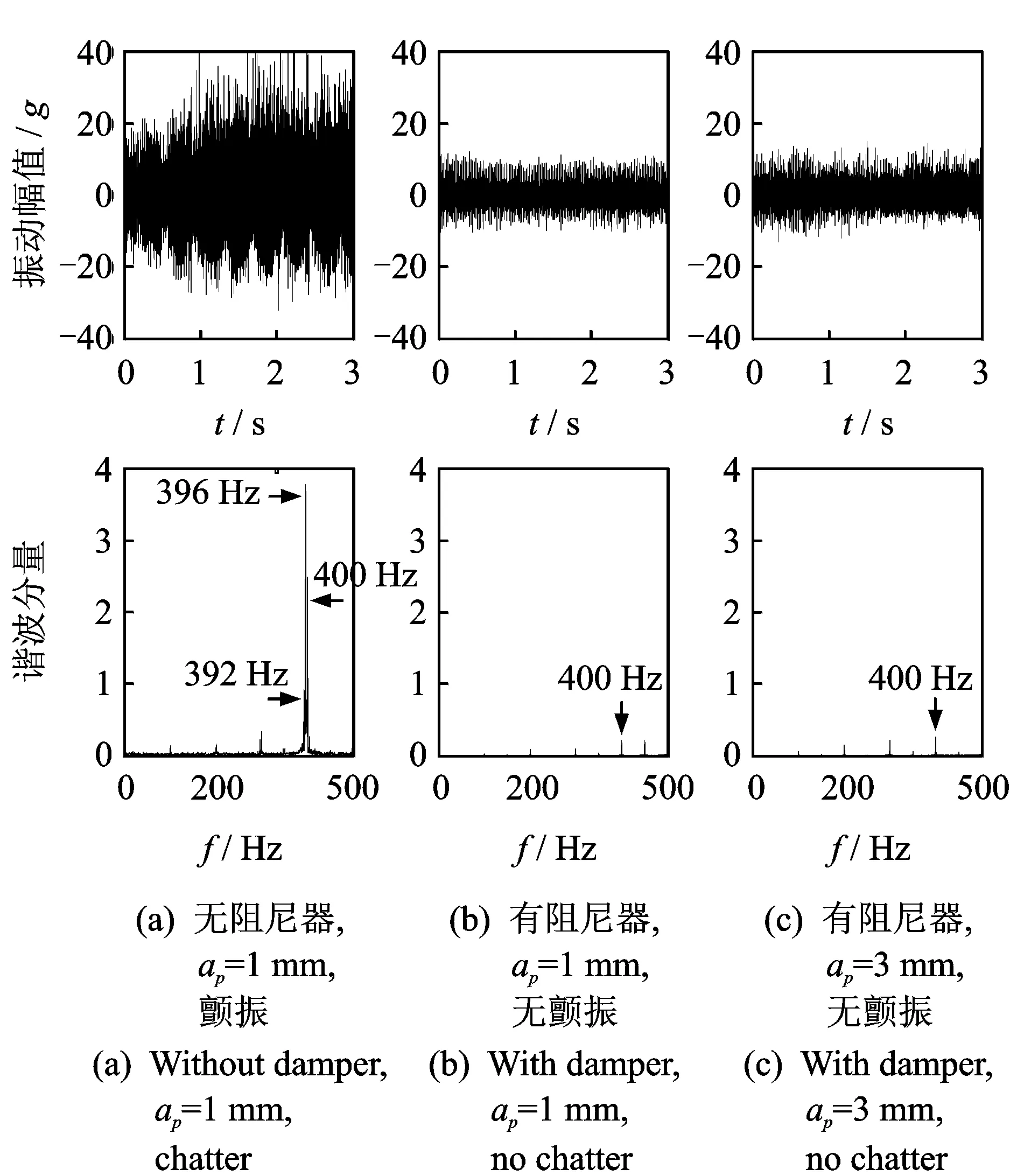
图7 切削过程中工件振动的加速度时频域信号Fig.7 Workpiece vibration in the time and frequency domain during the machining process

增加切深至3 mm，保持其余切削参数不变，工件振动的时频域信号如图7(c)所示。可见工件振动信号平稳，且最大谐波分量位于刀齿切削频率的4倍频处(400 Hz)，可推断切削过程处于稳态。切削实验表明，阻尼器的使用显著提升了薄壁零件的铣削稳定性。

4 结论

1) 该阻尼减振装置结构简单，使用方便，切削实验表明该装置可明显提升薄壁零件的铣削稳定性。

2) 理论推导表明，该装置所产生的阻尼力大小与磁铁切割磁力线的速度，即薄壁件的振动速度成线性关系，而且方向相反，所产生的作用效果与黏性阻尼相同。同时，该装置减振性能的发挥不受切削过程、材料去除等因素的干扰，具备一定的自适应性。

3) 该减振装置所产生的阻尼力还受到装置结构设计因素的影响，如：铜管材料、高度、壁厚等。在后续研究工作中将对此作进一步分析。

[1] 秦国华，吴竹溪，张卫红.薄壁件的装夹变形机理分析与控制技术[J].机械工程学报，2007,43(4)：211-216.

Qin Guohua, Wu Zhuxi, Zhang Weihong. Analysis and control technique of fixturing deformation mechanism of thin-walled workpieced[J]. Chinese Journal of Mechanical Engineering, 2007,43(4)：211-216. (in Chinese)

[2] Aoyama T, Kakinuma Y. Development of fixture devices for thin and compliant workpieces[J]. CIRP Annals - Manufacturing Technology, 2005,54(1):325-328.

[3] Shamoto E, Mori T, Nishimura K, et al. Suppression of regenerative chatter vibration in simultaneous double-sided milling of flexible plates by speed difference[J]. CIRP Annals-Manufacturing Technology, 2010,59(1):387-390.

[4] Ratchev S, Liu S, Becker A A. Error compensation strategy in milling flexible thin-wall parts[J]. Journal of Materials Processing Technology, 2005,162-163:673-681.

[5] Budak E. Mechanics and dynamics of milling thin walled structures[D]. Vancouver, Canada: The University of British Columbia, 1994.

[6] 梁睿君,叶文华.薄壁零件高速铣削稳定性预测与验证[J].机械工程学报,2009,45(11)：146-151.

Liang Ruijun, Ye Wenhua. Stability prediction for high-speed milling of thin walled structures and experimental validation[J]. Journal of Mechanical Engineering, 2009,45(11)：146-151. (in Chinese)

[7] Dohner J L, Lauffer J P, Hinnerichs T D. Mitigation of chatter instabilities in milling by active structural control[J]. Journal of Sound and Vibration, 2004,269(1-2):197-211.

[8] Rashid A, Nicolescu C M. Active vibration control in palletised workholding system for milling[J]. International Journal of Machine Tools and Manufacture, 2006,46(12-13):1626-1636.

[9] Duncan G S, Tummond M F, Schmitz T L. An investigation of the dynamic absorber effect in high-speed machining[J]. International Journal of Machine Tools and Manufacture, 2005,45(4-5):497-507.

[10]Rashid A, Nicolescu C M. Design and implementation of tuned viscoelastic dampers for vibration control in milling[J]. International Journal of Machine Tools and Manufacture, 2008,48(9):1036-1053.

[11]杨毅青，刘强，王民.面向车削颤振抑制的多重阻尼器优化设计[J].振动工程学报,2010,23(4):468-474.

Yang Yiqing, Liu Qiang, Wang Min. Optimization of multiple tuned mass dampers for chatter suppression in turning[J]. Journal of Vibration Engineering, 2010,23(4):468-474. (in Chinese)

[12]张三慧.大学物理学·电磁学[M].3版A版．北京：清华大学出版社，2008:410-422.

[13]Young H D, Freedman R A. University Physics[M]. 10th Edition. San Francisco: Addison-Wesley, 2000:21-32.