不确定性因素对某橡胶隔振器连接刚度的影响*

2015-06-09陈学前沈展鹏刘信恩王玉军

振动、测试与诊断 2015年3期

关键词：概率密度后验贝叶斯

陈学前，沈展鹏，刘信恩，王玉军

(中国工程物理研究院总体工程研究所绵阳，621999)

不确定性因素对某橡胶隔振器连接刚度的影响*

陈学前，沈展鹏，刘信恩，王玉军

(中国工程物理研究院总体工程研究所绵阳，621999)

设计了两类可以分离某橡胶隔振系统不确定性源的模态试验，并对每类试验进行了重复试验。根据试验结果，基于传统有限元模型修正方法对隔振系统的连接刚度进行了识别。基于贝叶斯方法并结合马尔可夫链蒙特卡罗(Markov chain Monte Carlo, 简称MCMC)抽样研究得到了连接刚度的概率密度，并结合随机变量的运算量化了各不确定性源对隔振器连接刚度的影响，最后通过确认试验验证了连接刚度不确定性模型的有效性。研究结果表明，隔振系统装配不确定性对连接刚度的影响比隔振器橡胶材料分散性的影响低一个数量级。

橡胶隔振器; 不确定性源; 贝叶斯方法; 不确定性量化

引言

在航空、航天及武器工程结构中，为了降低电子设备在实际工作环境中受到的各种振动，各种形式的隔振器被广泛采用，其中橡胶隔振器由于其结构简单、工艺性好、成本低等优点，是目前工程中应用最广泛的一类隔振器[1]。为了深入认识隔振器的静、动态力学行为，以便更好为设计服务，许多学者研究了其静、动态特性。张平等[2]利用某橡胶材料各种受力状态下的试验应力-应变关系曲线，计算了某汽车动力总成橡胶隔振器x，y和z方向静刚度。Richards等[3-4]设计了不同试验装置，研究了某橡胶隔振器的非线性静、动刚度，建立了连接的Maxwell模型。Ibrahim[5]对橡胶隔振器非线性本构模型的研究情况进行了总结。林松等[6]基于M-RT模型，研究了某橡胶隔振器的动刚度、动态阻尼与幅值、频率之间的关系。国内外对橡胶隔振器连接刚度及本构模型的研究，均没有考虑不确定性的影响，但由于橡胶材料本身力学参数就具有较大的分散性，且加工成隔振器构件后，这种不确定性将显现得更明显。为了研究并建立隔振器连接刚度的不确定性模型，需要开展多次重复试验研究，但由于时间及经费限制，试验次数通常不会很多，利用传统概率统计方法去量化不确定性刚度可能带来较大误差，此时通常采用贝叶斯方法来修正并量化不确定性参数。如Miranda等[7]采用贝叶斯方法，根据试验测得某地下岩石弹性模量的一批数据，修正并建立了该岩石弹性模量的概率模型。

笔者在对某橡胶隔振器连接结构进行大量模态试验的基础上，对每一试验工况下橡胶隔振器的连接刚度进行了识别，并基于贝叶斯方法并结合MCMC抽样建立了各不确定性源对隔振器连接刚度影响的概率模型，并且分析了各不确定性源对连接刚度的影响程度。

1 橡胶隔振器的模态试验

1.1 试验方法

用于橡胶隔振器连接结构的模态试验的试验装置包括Agilent公司的VXI/E1432A数据采集硬件、MTS I-deas Test数据采集分析软件、PCB力锤、压电加速度传感器、E3242A信号调理模块等，如图 1 所示。力锤敲击试件激起响应，加速度传感器测得的振动信号输入到VXI/E1432A数据采集系统，进行数据存贮及分析。

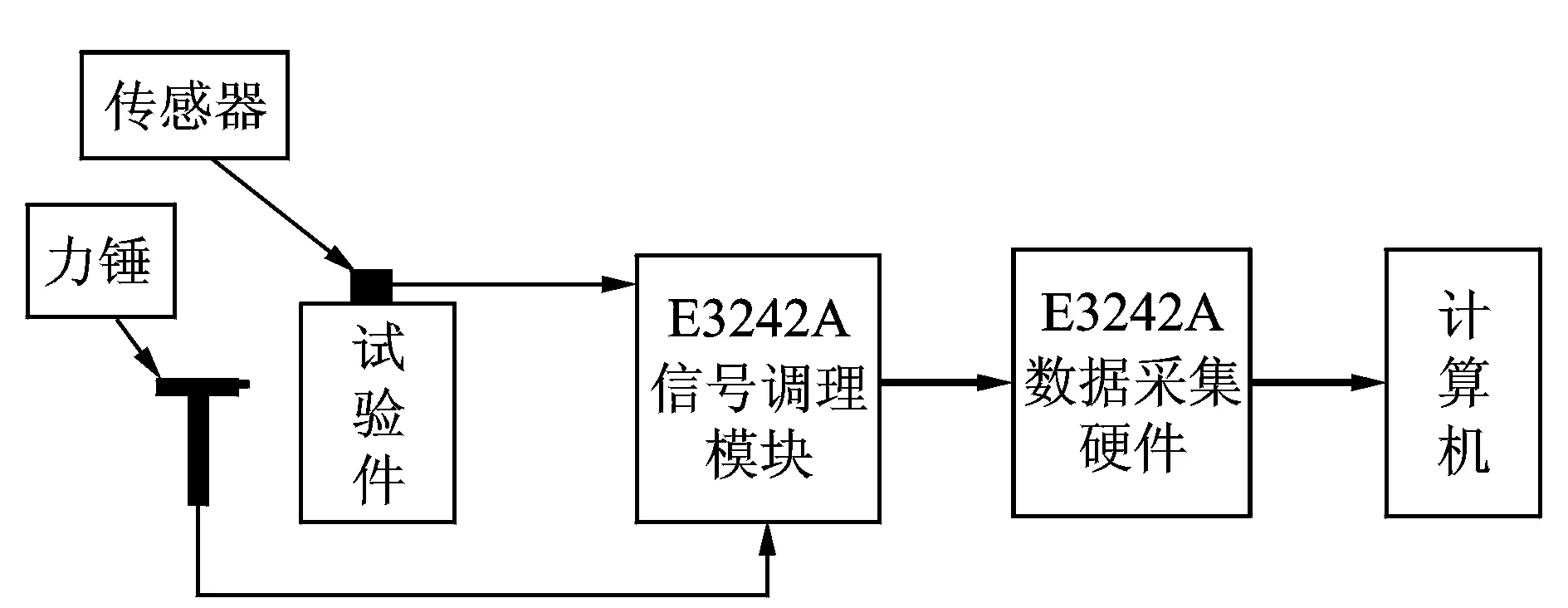
图1 试验测试系统配置图Fig.1 Test system scheme map

本试验用的隔振器由2个T型中空的橡胶构件通过钢制套筒组合而成，如图2所示。试验件由厚基础圆型钢板(直径为230 mm，厚为10 mm，质量为3.26 kg)、配重块(直径为79 mm，高度为26 mm，质量为1.12 kg)及4个隔振器组成。由于笔者主要研究不确定性因素对橡胶隔振器连接刚度的影响，故在试验装置中包含的不确定性因素越少越好。相比较，自由状态比固支状态的模态试验包含更少的不确定性因素，有利于更好分离影响隔振器连接刚度的不确定性因素，故通过橡皮绳悬挂试件对其进行自由状态模态试验，如图3所示。

图2 试验用隔振器Fig.2 Isolators used to test

图3 试件试验状态图Fig.3 Test state of the structure

通过力锤敲击配重块中心附近位置，采用单输入、多输出方式采集模态试验信号。由于笔者只关注各不确定性源对隔振器连接轴向刚度的影响，故只测试垂直于安装板方向的信号。由于下面识别隔振器连接刚度时是根据其轴向1阶伸缩频率，因此，对测试信号分析时采用单自由度模态拟合方法。

1.2 试验设计

为了量化研究各不确定性源对隔振器连接刚度的影响，需要分析试验过程中可能存在的不确定性源，并设计试验分离各不确定性源对刚度的影响。在该隔振器连接装置的模态试验中，不确定性源主要包括测试系统带来的不确定性、装配带来的不确定性以及隔振器自身材料的不确定性。根据工程经验，测试系统对这类结构的固有频率测试带来的不确定性很小，可忽略，笔者将其与装配不确定性一起考虑作为一个不确定性源。因此，设计两类模态试验，Ⅰ类试验用来研究测试系统及装配带来的不确定性，可以在某组隔振器选定的基础上，每次试验后重新拆装隔振器试件再重复模态试验，共重复25次，假定其影响隔振器连接刚度的不确定性量为A。Ⅱ类试验包含上述所有不确定性，即每次试验后重新拆装隔振器试件，且每次更换不同的隔振器，共重复25次，假定其影响隔振器连接刚度的不确定性量为B。每次装配时，保持隔振器相同的预压量。根据上述两个不确定性量，求出隔振器自身材料分散性对连接刚度的影响C=B-A。A，C为独立的随机变量，根据随机变量的运算[8]，可以很方便得到隔振器自身材料分散性对连接刚度影响的均值与方差

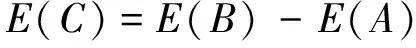
(1)

var(C)=var(B)-var(A)

(2)

1.3 试验结果

隔振器系统的连接刚度主要通过其1阶轴向伸缩振型对应的频率来识别。对测试点的传递函数进行模态拟合，得到各工况的传递函数，根据拟合曲线峰值识别系统的1阶固有频率。图4为工况2的传递函数曲线。根据两类试验中各工况的传递函数曲线，分析得到隔振器连接的1阶固有频率如表1所示。

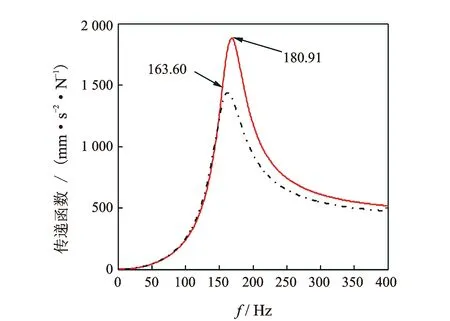
图4 工况2的传递函数曲线Fig.4 Curves of transfer functions in case 2

表1 隔振器的1阶固有频率

Tab.1 First inherent frequency of the isolator

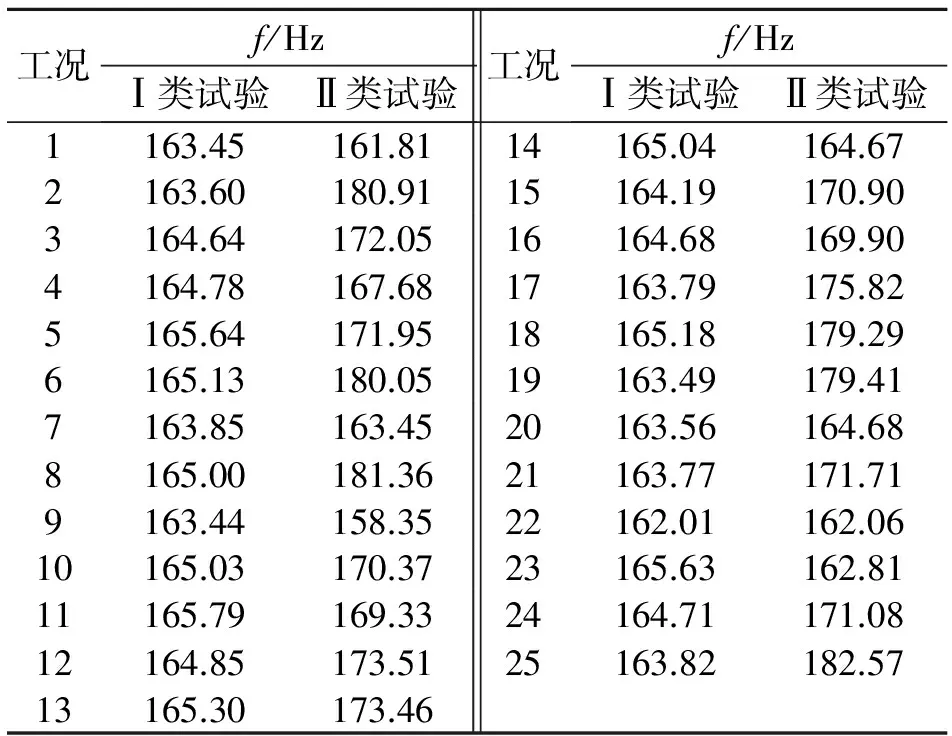
工况f/HzⅠ类试验Ⅱ类试验工况f/HzⅠ类试验Ⅱ类试验1163．45161．8114165．04164．672163．60180．9115164．19170．903164．64172．0516164．68169．904164．78167．6817163．79175．825165．64171．9518165．18179．296165．13180．0519163．49179．417163．85163．4520163．56164．688165．00181．3621163．77171．719163．44158．3522162．01162．0610165．03170．3723165．63162．8111165．79169．3324164．71171．0812164．85173．5125163．82182．5713165．30173．46

2 刚度的不确定性量化

2.1 参数识别

在ANSYS中建立试验件的有限元模型，其中基础钢板与配重采用SOLID45单元离散，隔振器采用COMBIN14弹簧单元离散。这样，系统中的不确定性就转化为弹簧刚度参数的不确定性。针对每一次试验工况，按照传统有限元模型修正方法，可直接调用ANSYS的优化模块完成刚度参数的识别，定义优化的目标函数为

(3)

其中：fc1，ft1分别为结构1阶固有频率的计算值与试验值。

根据上述参数识别策略，识别出两类试验各工况的弹簧刚度(隔振器刚度叠加不确定性源对刚度的影响值)，如表2所示。根据表2中的数据，结合贝叶斯推断，可完成刚度的量化。

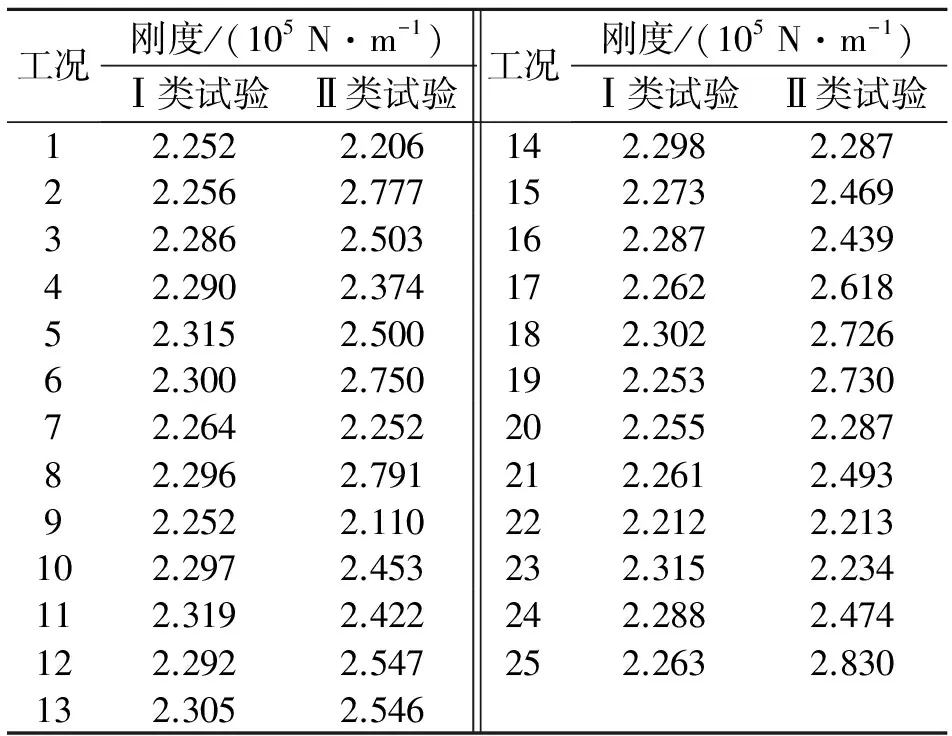
表2 弹簧刚度的识别结果

2.2 贝叶斯理论

若已知参数θ的先验分布为p(θ)，试验观察集为y，则参数的后验分布表示在获得试验观察信息y后参数θ的分布规律，可以用如下贝叶斯公式求得

(4)

其中：p(θ|y)为参数的后验分布密度函数；p(y|θ)为参数的似然函数。

考虑某随机系列X=(x1,x2，…,xn)的均值μ和标准差σ是未知的，且它们无先验信息。在没有任何信息可以利用的条件下叫做无信息先验，主要有Jeffreys先验分布和共轭先验分布等。下面仅考虑Jeffreys先验，在先验未知的情况下，均值μ和标准差σ的Jeffreys先验有如下形式

(5)

根据贝叶斯理论，未知均值及标准差的后验分布有如下形式

p(μ,σ2|X)∝p(μ,σ2)p(X|μ,σ2)∝σ-n-2×

(6)

(7)

(8)

2.3 刚度量化

后验概率在工程上常通过采用MCMC求解贝叶斯公式获得，常用的MCMC采样方法有Gibbs采样、Metropolis-Hastings算法等，笔者采用Gibbs采样方法[9]求解后验概率。针对Ⅰ类试验，通过求解贝叶斯公式获得其均值与标准差的后验分布，假定装配不确定性对刚度的影响是正态分布，重抽样得到该类试验下系统轴向刚度的概率密度,再将均值后验及刚度后验减去刚度后验的均值(Ⅰ类试验中隔振器的刚度)，得到不确定性对刚度影响的概率密度,如图5所示。采用同样的抽样方法可以得到考虑所有不确定性的Ⅱ类试验中系统轴向刚度的概率密度，如图6所示。根据图5、图6中各曲线数据，再结合式(1)、式(2)可求出隔振器自身材料分散性对连接刚度影响的均值与标准差的概率密度，并假定其为正态分布，进而得到隔振器自身材料分散性对连接刚度影响的概率密度，如图7所示。

从图5(c)及图7(c)可以看出，系统装配不确定性对连接刚度的影响比隔振器自身材料不确定性对刚度的影响要低一个数量级。

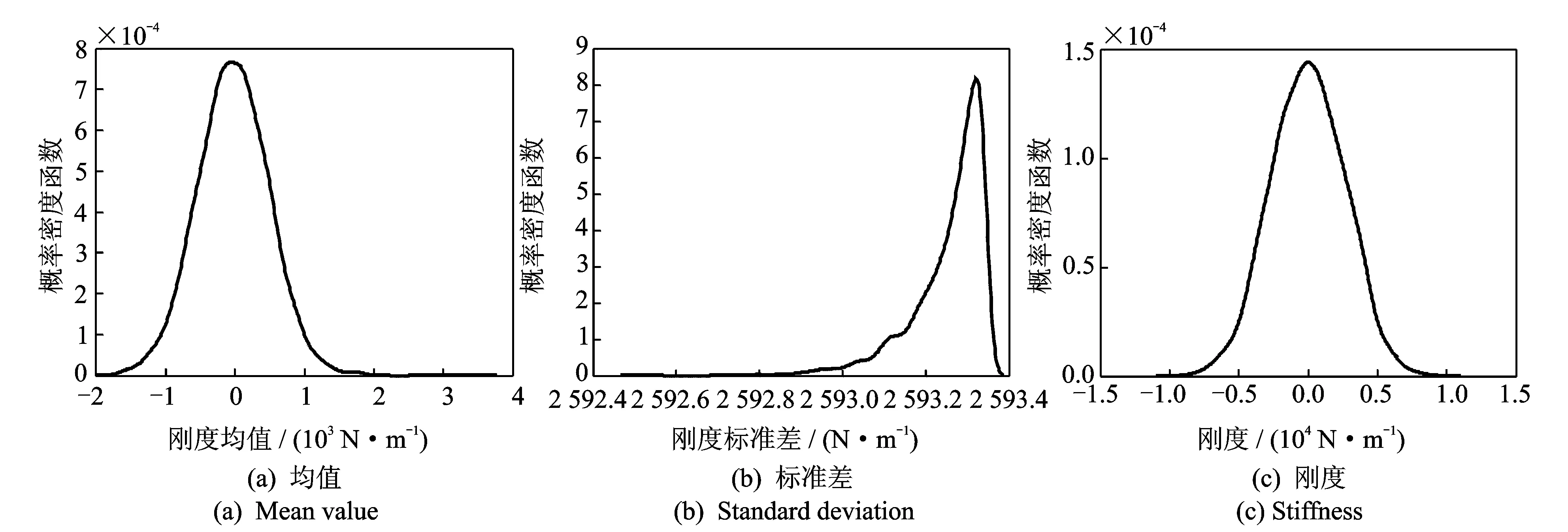
图5 装配不确定性对系统轴向刚度影响的概率密度Fig.5 Probability density of the axial stiffness affecting by the assembling uncertainty

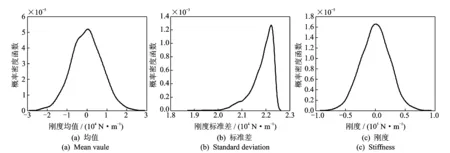
图6 所有不确定性对系统轴向刚度影响的概率密度Fig.6 Probability density of the axial stiffness affecting by all of the uncertainty

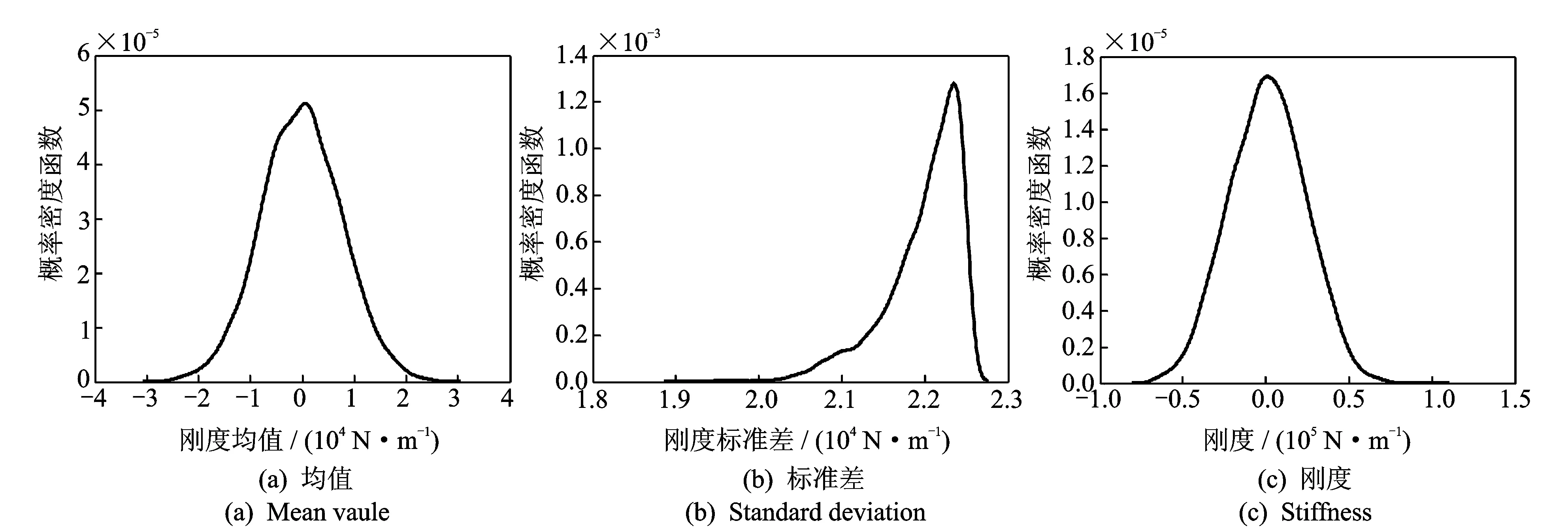
图7 隔振器自身材料不确定性对系统轴向刚度影响的概率密度Fig.7 Probability density of the axial stiffness affecting by the uncertainty of the isolator material

2.4 模型确认

通过对隔振器自身材料与装配不确定性对隔振系统连接刚度的影响进行量化，得到了各自的概率模型。为了验证量化结果的正确性，另外开展了两个工况的Ⅱ类试验，得到试验系统1阶固有频率分别为161.45，170.51 Hz。同时，基于所建立各不确定性源的概率模型，通过蒙特卡罗抽样仿真得到系统的1阶固有频率的概率密度曲线，如图8所示。其95%置信区间为[156.33 184.97]，验证试验结果全部落在该区间。根据模型确认中的95%置信区间确认度量准则[10-11]，认为对各不确定性源的量化结果是正确的。

图8 系统1阶固有频率计算结果的概率密度及95%置信区间Fig.8 Probability density and 95% confidence interval of the first inherent frequency computed

3 结束语

笔者基于模态试验研究了某橡胶隔振器系统的主要不确定性源对其连接刚度的影响，采用贝叶斯方法并结合MCMC抽样，量化了对刚度影响的不确定性。通过对比刚度的量化模型与验证试验结果，确认了量化模型的有效性。量化结果表明，试验系统及装配不确定性引起的不确定性比隔振器自身材料的不确定性要低一个数量级。通过研究可知，橡胶隔振器连接刚度的不确定性是客观存在的，工程中根据设计要求选择相应隔振器时需要考虑这一因素对隔振效果的影响。

[1] 张阿舟，姚起航.振动控制工程[M].北京：航空工业出版社，1989:104-147.

[2] 张平，柴国钟，潘孝勇，等.橡胶隔振器静态特性计算方法研究[J].振动、测试与诊断，2010，30(2):105-110.

Zhang Ping, Chai Guozhong, Pan Xiaoyong, et al. Investigation on calculation method for the static characteristics of a rubber isolator[J]. Journal of Vibration, Measurement & Diagnosis,2010，30(2):105-110. (in Chinese)

[3] Richards C M, Singh R. Characterization of rubber isolator nonlinearities in the context of single-and multi-degree-of-freedom experimental systems[J]. Journal of Sound and Vibration, 2001,247(5):807-834.

[4] Zhang Jie, Richards C M. Parameter identification of analytical and experimental rubber isolators by Maxwell models[J]. Mechanical Systems and Signal Processing, 2007,21:2814-2816.

[5] Ibrahim R A. Recent advances in nonlinear passive vibration isolators[J]. Journal of Sound and Vibration, 2008,314:371-452.

[6] 林松，张鲲，孙磊，等.橡胶隔振器动态特性的本构研究[J]．振动与冲击，2011，30(3):177-180.

Lin Song, Zhang Kun, Sun Lei, et al. Study on dynamic characteristics of rubber isolator[J]. Journal of Vibration and Shock，2011，30(3):177-180. (in Chinese)

[7] Miranda T, Gomes Correia A, Ribeiro e Sousa L. Bayesian methodology for updating geomechanical parameters and uncertainty quantification[J]. International Journal of Rock Mechanics & Mining Sciences, 2009,46:1144-1153.

[8] 庄表中，梁以德，张佑启.结构随机振动[M].北京：国防工业出版社，1993:218.

[9] David M W, Pérez-Barbería F J, Glenn M. Stochastic modelling of ecological processes using hybrid Gibbs samplers[J]. Ecological Modelling, 2006,198(2):40-52.

[10]Oberkampf W L, Matthew F B. Measures of agreement between computation and experiment: validation metrics[J]. Journal of Computational Physics, 2006,217:5-36.

[11]Roy C J, Oberkampf W L. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200:2131-2144.