基于车内综合声场贡献分析的车身板件声振优化

靳 畅，周 鋐

(同济大学新能源汽车工程中心，上海 201804)



2015242

基于车内综合声场贡献分析的车身板件声振优化

靳 畅，周 鋐

(同济大学新能源汽车工程中心，上海 201804)

在应用声传递向量技术对某商用客车的车内噪声进行板件声学贡献分析的基础上，提出了引入特征频率计权系数和场点权重系数确定多特征频率下对车内综合声场声学贡献量最大的关键车身板件的方法。接着采用中心组合设计通过最小二乘拟合建立了以关键板件振速和1阶模态频率为目标，板件与阻尼层厚度为变量的非线性的响应面模型，通过优化确定了变量的最佳组合。优化方案的实车试验结果显示车内噪声改善效果明显。

车身板件；声学贡献；声传递向量；中心组合设计；响应面模型；优化

前言

汽车车身大部分由薄钢板构成，当其受到发动机或路面不平引起的边界载荷激励时引起板件结构振动向车内辐射声能形成车内噪声，因此板件是车内结构声[1]传递的一个重要环节。确定对车内关键位置噪声贡献最大的结构板件是进行车内降噪的重要前提，之后对关键板件的振动抑制是降低车内低频噪声的有效手段。文献[2]中基于有限元法(FEM)预测了车身板件辐射引起的100～500Hz车内噪声，但其研究中以激振器作为加载而非实际的载荷。文献[3]和文献[4]中采用了基于边界元法(BEM)[5]和有限元法的声传递向量(ATV)法[6]对怠速时的车身板件声学贡献做了相应的研究，但都只针对车内单个噪声场点或单个问题特征频率，无法体现板件在多个特征频率下对整体车内声场的声学贡献量。文献[7]中以“声学贡献和”和“声场总贡献”来衡量车身板件对乘员室声压响应的声学贡献，但在板件降噪措施上并未做系统的优化分析。本文中在声传递向量法分析板件声学贡献的基础上，提出了引入特征频率计权系数和场点权重系数以确定多特征频率下车内综合声场声学贡献量最大的关键车身板件，并提出了基于非线性响应面模型的近似拟合来建立板件振速、1阶模态频率与板件、阻尼层厚度之间的关系，系统地优化了板件与阻尼层厚度组合以达到最佳降噪效果。

1 声传递向量板件声学贡献

声传递向量(acoustic transfer vector, ATV)法是有限元-边界元耦合分析法的发展，声传递向量ATV在场点声压与结构振动表面之间建立了一种对应关系，其物理意义可以理解为单元在特定频率下的单位速度在场点上引起的声压值[6]。将车身板件划分成K个有限单元，车内某场点的总声压p可以表示为这K个有限单元振动引起的声压的矢量叠加，则在某点处的声压为

(1)

式中：K为单元总数；ve,j(ω)为单元j的法向振速。

单元e对某场点的声学贡献量De是该单元振动引起的那部分声压pe在该点总声压p矢量上的投影，板件区域由k个单元划分组成，其归一化的声学贡献量为

(2)

根据声传递向量法对某商用客车以70km/h的车速在粗糙路面行驶工况下进行板件声学贡献分析。为了反映整个车内声场特性在驾驶员和第1～5排乘客右耳5个位置布置噪声场点测点，试验在半消声室内的比利时路面底盘测功机上进行，采用LMS公司SC305数据采集系统测量噪声，由分析软件Test.Lab计算的A计权噪声自功率谱如图1所示，在43，75，188和225Hz处有明显噪声峰值，将其作为分析的特征频率。建立车身的结构和声腔模型，结构有限元模型材料参数如表1所示，车内声腔边界元模型和板件划分区域见图2。在70km/h下经过轮胎、悬架和车架传至车身底部4个连接点(图3)的3方向激励力(图4)作为模型的载荷输入，采用LMS Virtual.Lab软件计算声传递向量后得到各特征频率处车内各场点的板件声学贡献，如图5所示。由图可见，同一场点在不同特征频率处的贡献是不一样的，甚至会有正负之差。因此应该综合考虑板件、场点和频率因素的不同，避免在抑制板件振动降低某一频率声压响应的同时，造成另一频率位置的噪声恶化。

表1 车身模型主要材料参数

2 多特征频率车内综合声场声学贡献

根据上述分析，车身板件在各特征频率下对各场点的声学贡献是不同的。但可以根据场点和特征频率在车内综合声场中的重要性，赋予每个场点和每个响应特征频率不同的计权。本文中提出了一个车内整体声学贡献的表达式为

(3)

式中：(pc)Total为所有板件在多特征频率车内综合声场下的贡献量集；(pc)i,N为所有划分的板件对某场点N声压响应中的某特征频率i处的声学贡献量；n为板件贡献量分析关心的特征频率数量；m为场点数量；αi为每个特征频率的计权系数，表示对特征频率的不同重视程度；βN为第N个场点的权重系数。权重系数βN可根据在场点N处的主要特征频率总声压响应占所有场点声压响应总和比例的大小而确定，可表示为

(4)

式中DN,i为场点N在特征频率i下的声压频率响应值。

式(3)的多特征频率车内综合声场贡献量可全面地表征板件对车内声场整体声学特性的影响，其量值表示该板件对车内声场整体声学特性贡献量的大小。结合所研究的车辆，板件区域数量为36，n=4，m=5；对每个特征频率都给予相同的重视程度，αi=1；βN则按式(4)计算得到，见表2。板件的整体声学贡献量排序结果如图6所示，6号板件即左后顶围区域为对车内整体声场具有最大的声学正贡献量，因此需要对其进行修改优化。

表2 各场点计权系数βN

3 基于非线性响应面模型的板件振速优化

根据声传递向量原理，板件的振速直接关系到车内的声学特性，抑制板件的振动是车内降噪的有效手段。根据研究[8]，改变板件厚度和铺设阻尼层都会对振速产生抑制作用。因此，通过修改关键板件和阻尼层厚度来优化结构的声振特性以降低车内噪声。

3.1 非线性响应面模型

在结构优化之前首先要明确板件振速与厚度间定性和定量的关系。对于铺设阻尼层的车身板件复合结构所涉及的结构振动优化问题一般是非线性且非常复杂的，采用仿真计算的方法费时费力，为降低优化的复杂程度，减少计算时间，近似拟合是一个有效的方法，响应面法(response surface method, RSM)能够很好地表述目标函数和约束函数与设计变量之间的非线性关系[9-10]。其基本思想是通过有限的输入变量和输出响应的样本点进行回归分析，拟合出解析表达式来代替真实响应面。

一般地，系统的响应量y与设计变量(x1,x2,…,xk)可以表示为

y=g(x1,x2,…,xk)+ε

(5)

通过有限样本点而得的系统函数f(x1,x2,…,xk)也可写为

y=f(x1,x2,…,xk)+ε

(6)

式中ε表示响应的观测误差或噪声。f(x1,x2,…,xk)是对g(x1,x2,…,xk)的近似，对于非线性的响应关系，用2阶多项式表示为

(7)

响应面法建模的关键是模拟的准确性和效率，利用实验设计可以用有限的数值计算样本点保证较高的响应面模型精度。基于中心组合设计(CCD)[11]的2阶响应面建模使用较少的实验点，并能保证回归分析的精度。通过实验设计拟合出响应面模型，从而确定设计变量的最佳组合，结构的优化问题就变成一个纯粹的数学优化问题，其流程如图7所示。

以关键板件的单元最大振速vn和阻尼复合板件的1阶模态频率ω作为响应面模型的分析目标，选取板件厚度t1和阻尼层厚度t2作为设计变量。关键板件6号左后顶围的基础厚度为0.8mm，考虑到工程实际中板件厚度可改变的范围，表3列出了设计变量t1和t2的初始取值。将设计变量转换为无量纲的编码以方便进行中心组合实验，新的无量纲变量为

(8)

表3 设计变量初始值

原设计变量初始值转变为如表4的3种无量纲初始水平。

采用两个变量一个中心点的中心组合设计方法，选取9个数值仿真样本点进行回归分析。对应左后顶围关键板件在车身有限元模型相应位置以体(Solid)单元模拟沥青材料阻尼层，设置其弹性模量为71MPa，密度为1 200kg/m3，泊松比为0.45，阻尼材料的损耗因子取常数0.8。用公共节点法来模拟阻尼与板件的粘接作用。以70km/h下车身工作力边界载荷添加20～300Hz的激励计算9组设计变量下关键板件的vn和ω，结果如表5所示。

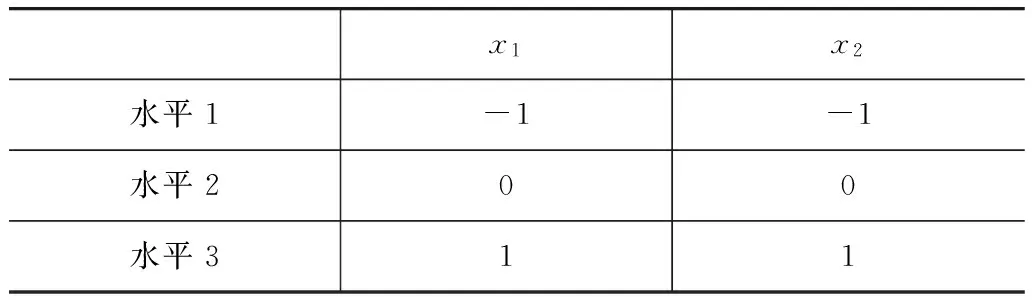
表4 中心组合设计的设计变量取值

表5 中心组合设计的数值计算样本

取得了分析目标和设计变量的样本数据后，就可进行回归分析，确定它们之间的定量关系，建立响应面模型。考虑到目标与变量之间关系较为复杂，因此采用式(7)的二阶多项式来拟合响应面。多项式中的各项系数可用基于最小二乘法的回归分析来确定[12]，未知系数β的解为

(9)

对于二次多项式，有

X=[1,x1,…,xn,x12,x1x2,…,x1xn,…,xn2]T

未知系数的解为

(10)

式中：n为样本点总数；k为设计变量数。

以中心组合设计结合最小二乘法得到板件振速2阶多项式响应面拟合为

vn= 31.13-2.34x1-1.53x2+1.07x1x2-

0.21x12-1.14x22

(11)

板件1阶模态频率2阶多项式响应面拟合为

ω= 29.14+6.84x1-0.77x2-0.54x1x2-

1.46x12+0.21x22

(12)

为检验所得的响应面模型的正确性，在设计变量取值范围内任意取3组设计变量组合(x1,x2)进行数值计算，并与响应面模型的计算结果相比较并计算偏差，结果如表6和表7所示。可以看出，结果偏差都在3%以内，证实响应面模型能较真实地反映阻尼复合板件的响应特性。

表6 板件最大振速vn数值计算与响应面计算结果对比

表7 板件1阶模态频率ω数值计算与响应面计算结果对比

图8和图9直观地显示了分析目标响应面模型的图形。可以看出，当板件厚度一定且较薄时(接近-1)阻尼复合板件的振速随阻尼层厚度的增加而降低；当板件厚度较厚时(接近1)振速随阻尼厚度先升高后降低；当阻尼层厚度一定时，振速随基层厚度的增加而快速下降。1阶模态频率随板件厚度的减小而迅速降低，同时板件厚度对1阶模态频率的影响要远大于阻尼厚度。可以看到，设计变量的变化对分析目标的影响是复杂的，因此需要确定变量的最佳组合来优化阻尼复合板件结构，从而达到减振降噪的目的。

3.2 板件振速优化

建立响应面模型的最终目的就是找出变量在设计范围内对分析目标的最优点，板件振速是影响其向车内辐射噪声的主要因素，因此将其作为优化的目标。而1阶模态频率直接反映了板件的结构刚度，应保证优化后不低于原状态1阶模态频率，将其作为约束条件之一。另外，考虑到轻量化的需求，阻尼复合后的板件质量也不能过大，将其设为不高于原质量的50%作为另一个约束条件。关键板件基础厚度为0.8mm，质量为8.1kg，面积为1.267m2，1阶模态频率为32.7Hz。优化设计的变量为板件厚度x1和阻尼厚度x2。由此建立如下的优化模型：

(13)

式(13)的数学模型属于带约束的最小化优化问题，采用MATLAB的fmincon优化函数[13]进行求解。

整个优化函数的详细表达式为

(14)

令初始值x1=0，x2=0，优化求解得

(15)

根据式(9)将无量纲的变量转换为实际厚度得到：

(16)

根据工程实际，取板件厚度为整数t1=0.9mm后，由响应面模型计算得到的板件振速vn=29.7625mm/s。这就是考虑了板件1阶模态和板件质量约束条件下的厚度最优组合。

4 实车试验验证

针对上文的优化结果对实车进行方案实施并试验。改变左后顶围区域板件厚度为0.9mm并铺设沥青阻尼层，厚度2mm，如图10所示。按照优化前相同的运行工况和场点布置进行车内噪声试验，由于是考察车内多个场点改善的综合效果，在此引入一个综合性的指标体现措施前后的差别：

(17)

式中：psyn为车内多场点的综合噪声指标；pN(ω)为场点N的噪声频谱。

图11为板件优化前后车内多场点综合噪声频谱的对比，表8列出了优化前后4个特征频率下以及总噪声的变化，图12为每个场点总声压级的变化。可以看出，改善的效果明显。因此，本文中提出的基于车内综合声场声学贡献分析的车身板件声振优化方法是有效的。

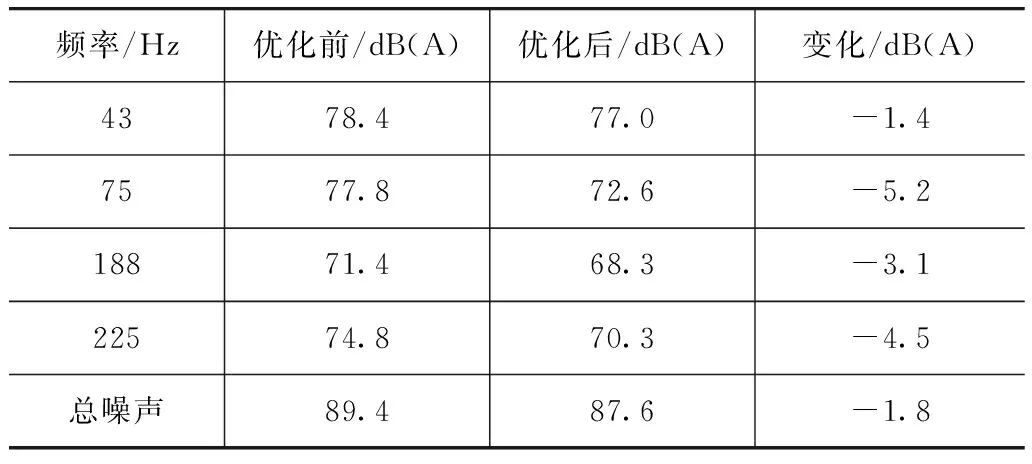
频率/Hz优化前/dB(A)优化后/dB(A)变化/dB(A)4378.477.0-1.47577.872.6-5.218871.468.3-3.122574.870.3-4.5总噪声89.487.6-1.8

5 结论

(1) 在采用声传递向量法分析板件声学贡献的基础上，提出了引入特征频率计权系数和场点权重系数来确定多特征频率下对车内综合声场声学贡献最大的关键车身板件。

(2) 提出基于响应面法寻求板件优化的目标。建立了以关键板件振速与1阶模态频率为目标、板件和阻尼厚度为变量的非线性响应面模型。该模型显示，当板件厚度一定且较薄时阻尼复合板件的振速随阻尼层厚度的增加而降低；当板件厚度较厚时振速随阻尼厚度先升高后降低；当阻尼层厚度一定时，振速随基层厚度的增加而快速下降。1阶模态频率随板件厚度的减小而迅速降低，同时板件厚度对1阶模态频率的影响要远大于阻尼厚度。

(3) 以板件振速最小化为目标，1阶模态频率和质量为约束条件确定了板件与阻尼厚度的最优组合。实车试验结果显示优化方案对各特征频率和各场点的车内噪声改善明显。因此，本文中所提出的基于车内综合声场的响应面板件优化是有效可行的，为车身板件的减振降噪提供了一种较为完整、系统的优化方法。

[1] 庞剑,湛刚,何华.汽车噪声与振动[M].北京:北京理工大学出版社,2006:312-319.

[2] Teik C Lim. Automotive Panel Noise Contribution Modeling Based on Finite Element and Measured Structural-acoustic Spectra[J]. Applied Acoustics,2000,60:505-519.

[3] 赵静,周鋐,梁映珍,等.车身板件振动声学贡献分析与优化[J].机械工程学报,2010,46(24):96-100.

[4] 王二兵,周鋐,徐刚,等.基于车身板件声学贡献分析的声振优化[J].江苏大学学报,2012,33(1):25-29.

[5] 靳晓雄,张立军.汽车噪声的预测与控制[M].上海:同济大学出版社,2004.

[6] 李增刚,詹福良.Virtual. Lab Acoustics声学仿真计算高级应用实例[M].北京:国防工业出版社,2010.

[7] 韩旭,林海东,郭永进,等.基于壁板声学贡献分析的轿车乘员室声场降噪研究[J].上海交通大学学报,2008,42(8):1254-1258.

[8] 梁新华.汽车车身薄壁件阻尼复合结构振动-声学分析与优化[D].上海:上海交通大学,2007.

[9] 王永菲,王成国.响应面法的理论与应用[J].中央民族大学学报(自然科学版),2005(3):236-240.

[10] Roux W J, Stander N, Haftka R T. Response Surface Approximations for Structural Optimization[J]. Int J Numer Methods Eng,1998,3(42):517-534.

[11] 陈立周.稳健设计[M].北京:机械工业出版社,2000.

[12] 邱秩兵.实验设计与数据处理[M].安徽:中国科学技术大学出版社,2008:185.

[13] 曹卫华,郭正.最优化方法及MATLAB实现[M].北京:化学工业出版社,2005:78-89.

Vibro-acoustic Optimization of Vehicle Body Panels Basedon Overall Interior Noise Contribution Analysis

Jin Chang & Zhou Hong

CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804

Acoustic transfer vector technique is applied to an analysis on panel acoustic contribution to the interior noise of a commercial bus. Based on the analysis, a scheme is proposed of introducing weighting coefficients for characteristic frequencies and field points to determine the dominant body panels having the most acoustic contribution to overall interior sound field. Then central composite design and least square fitting are adopted to build a nonlinear response surface model with the vibration velocity of key panels and the 1st order modal frequency as objective and the thicknesses of panels and damping layers as design variables, and an optimum combination of variables is determined by optimization in the end. The results of real vehicle test with optimized scheme demonstrate an apparent noise improvement effect.

vehicle body panel; acoustic contribution; acoustic transfer vector; central composite design; response surface model; optimization

原稿收到日期为2014年5月19日，修改稿收到日期为2014年8月4日。