基于动态规划算法的并联混合动力客车控制策略优化*
2015-06-09高印寒王庆年曾小华宋大凤
巴 特,高印寒,王庆年,曾小华,宋大凤
(吉林大学,汽车仿真与控制国家重点实验室,长春 130025)
2015229
基于动态规划算法的并联混合动力客车控制策略优化*
巴 特,高印寒,王庆年,曾小华,宋大凤
(吉林大学,汽车仿真与控制国家重点实验室,长春 130025)
针对传统动态规划算法中存在的成本函数受SOC变化影响大、权系数的确定缺乏理论依据等问题,本文中为一并联混合动力客车提出了以等效油耗为成本函数和采用割线迭代法计算权系数的动态规划优化算法。根据一定假设搭建SIMULINK简化模型,按照成本函数和反向递推公式求取最优控制变量集合,并提炼出有效的控制规则,以改进控制策略。SIMULINK仿真和SIMULINK/CRUISE联合仿真两种结果表明,在中国城市综合工况下,动态规划优化算法比传统动态规划算法分别节油6.06%和3.23%,说明本文所提出的优化算法更加合理和节能。
混合动力客车;动态规划;控制规则;算法优化
前言
能量控制策略是影响混合动力汽车燃油经济性的主要因素之一,为使车辆更加节油,控制策略也在不断优化,从瞬时最优算法到全局最优算法。而全局最优算法中以动态规划算法最为突出,因其优化效果明显已成为国内研究热点,但动态规划算法也存在一定的问题和缺点。如针对动态规划计算量大、耗时长问题,文献[1]~文献[3]中根据电池充放电电流确定不同时刻SOC的可行域,减小计算量;文献[4]中采用较为稀疏的变量网格来减少计算量,再通过多次迭代提高计算精度,逼近最优解。对于从最优变量中提取控制规则所需工作量大的问题,文献[4]中应用神经网络提炼控制规则,提高工作效率;文献[5]中在规则提炼上提出了功率分配比,既能表示所处的模式,又可明确转矩分配。针对动态规划算法不适用于不确定工况的实车控制问题,文献[6]和文献[7]中利用马尔科夫模型预测未来工况计算功率分配,在一定程度上适应实际工况的不确定性;而文献[8]中为了解决维灾难采用了神经元动态规划来替代基于马尔科夫模型的随机动态规划,更是提高了策略的实时性;相对马尔科夫和神经预测方法,文献[9]和文献[10]中采用GPS和GIS预测未来工况,并结合动态规划优化控制。然而,对于优化动态规划成本函数和权系数计算方法的研究却较为少见,其中文献[11]中采用间接控制,以功率损失替代成本函数中的油耗项,获得了更好的优化效果,但这两种成本函数本质上是相同的,都以SOC罚函数为修正项。SOC罚函数是SOC变化量的平方项,所以传统成本函数值受SOC变化影响较大,进而将影响动态规划的全局优化效果。另一方面成本函数中各项权系数的计算方法也并不明确且缺乏理论依据,权系数的确定直接关系到动态规划的优化效果和SOC的平衡。
通过对上述文献研究现状的分析,本文中针对ISG并联混合动力系统提出以等效油耗为成本函数和割线迭代法为权系数计算方法的动态规划优化算法,并结合SIMULINK中搭建的简化模型,依据成本函数和反向递推公式求解最优控制变量解集,进而提炼控制规划改进控制策略,通过在SIMULINK和CUIRSE中与传统动态规划算法仿真对比,验证了优化算法的合理性和节能优势。
1 整车建模
本文中的混合动力客车采用单轴并联的结构,ISG电机与发动机通过离合器相连,离合器控制发动机是否参与驱动,电机后连接5挡变速器输入轴,通过变速器减速增矩可以对发动机及电机的工作点进行调节,系统结构如图1所示。
由于动态规划算法建模的目的是确定系统能量分配,对于变速器和离合器动态过程可以忽略,所以假设:忽略变速器、主减速器的转动惯量;变速器换挡可以在瞬间完成;离合器的接合和分离状态与发动机起动和关闭相对应,且接合和分离可以瞬间完成,效率为100%;轮胎滚动阻力系数为恒定;路面附着力系数充分大。
1.1 发动机模型
由于发动机理论建模须基于很多假设,会降低模型精度,而且复杂的解析表达式会降低计算速度,所以采用实验建模法依据实验数据建立查表性质模型,其输入输出关系可以精确表示发动机的稳态特性。假设发动机已经完全预热,其外特性和万有特性如图2所示。
1.2 电机模型
电机建模与发动机相似,也采用实验数据建模法,主要考虑电机机械特性,其功率表达式为
(1)
其中ηm=f(Tm,ωm)
(2)
式中ωm,Tm和ηm分别为电机的转速、转矩和效率。电机效率是电机转矩和转速的函数。函数f由电机实验数据确定,通过查取二维表实现,电机万有特性如图3所示。
1.3 电池模型
电池可以简化为内阻模型,如图4所示。忽略温度对开路电压和内阻的影响,则电池组SOC的计算公式为
SOC(k+1)=SOC(k)-
(3)
式中:开路电压Uoc和内阻Rint为SOC的函数;Rt为终端电阻;Qmax为电池组的最大容量。
1.4 传动系模型
传动系模型包括离合器、变速器和驱动桥,其中对离合器模型进行了一定的简化,其开度γcl满足:
(4)
其中开度为1代表离合器分离,0代表离合器接合,假设离合器可以瞬间分离和接合。而变速器也假设可以瞬间完成换挡,所以实际挡位gact等于目标挡位gdes。
传动系中车轮的转速ωw可由动力学方程计算:
(5)
其中Td=igi0ηT(Te+Tm)
(6)
式中:Tb为所有制动器制动转矩;rw为车轮半径;Ff和Fw分别为车辆滚动阻力和空气阻力;δ为汽车旋转质量换算系数;m为整车满载质量;Td为主减速器输出转矩;Te和Tm为发动机和电机转矩;ig和i0为变速器和主减速器的传动比;ηT为传动系效率。
2 动态规划算法优化
动态规划算法是在约束条件下多目标优化的问题。多目标寻优须要确定目标函数和权系数,这关系到动态规划算法的优化效果,而在传统算法中存在着目标函数受SOC变化影响大、权系数确定方法缺乏理论依据的问题,所以目标函数和权系数是本文中优化的关键方向。
2.1 目标函数的确定
动态规划寻优求解首先需要明确目标函数,即成本函数,其0~N时刻的成本函数可表示为
(7)
x(k+1)=f(x(k),u(k)),k=0,1,…,N-1
(8)
式中:Lk为单步状态转移成本函数;J为累积成本函数;x(k)为k时刻的系统状态变量,即电池组荷电状态SOC;u(k)为系统控制变量,包括发动机节气门开度γe和变速器目标挡位gdes。
在单步寻优过程中,除了保证油耗最少,还需要考虑SOC平衡和尽量减少换挡操作,所以传统算法中单步成本函数可表示为
Lk(x(k),u(k))=Lfuel(k)+αLSOC(k)+βLgs(k)
(9)
式中:Lfuel,LSOC和Lgs分别为燃油消耗函数、SOC罚函数和换挡罚函数;α和β分别为罚函数的权系数。为使SOC快速返回参考值SOCref,SOC罚函数通常为SOC变化量的平方:
LSOC(k)=(SOC(k)-SOCref)2
(10)
然而这种成本函数通常受SOC变化量的影响较大,这将导致电能的不合理使用,从而削弱动态规划的全局优化效果,说明采用SOC罚函数的成本函数不能找到使全局油耗最少的最优解。而全局油耗最少是能量分配策略的目标,所以设置合理的成本函数的前提是清楚这一目标的实质,那么能量分配策略的目标函数可表示为
(11)
(12)

ΔQe(k)=-ΔEb(k)/keq(k)
(13)

(14)
从式(14)可以发现求全局油耗最小值问题的等价式与油电转换系数keq密切相关,可以尝试以等效油耗函数为成本函数。而成本函数的作用是设置与能量分配策略目标本质上相同的标准,确定最优控制变量。如果等效油耗成本函数满足图5所示的验证条件,则可证明它更加合理。
假设存在工况油电转换系数Keq,以其倒数1/Keq为权系数,它与电能消耗函数Lele(k)的乘积作为等效油耗成本函数中的罚函数,可使电池SOC在工况前后一致,且初步的研究没有发现频繁换挡现象,所以成本函数可表示为
ΔEb(k)/Keq)
(15)
(16)
因为式(15)的成本函数可使SOC平衡,所以存在如下条件:
(17)
则式(16)可进一步化简为
(18)
式(18)的推导结果与式(14)完全相同,说明等效油耗成本函数在保证SOC平衡的前提下,可使动态规划算法的目标函数和能量分配策略所需实现的全局油耗最少目标相同,所以这种成本函数更加合理。
2.2 反向递推求最优解
依据Bellman原理,在明确成本函数后,需要在约束条件下递推寻优,条件如下:
(19)
然后从第N步开始反向递推求最优解。
第N步:
(20)
第k步(0≤k (21) (22) 然而所求变量为最优控制变量的前提是权系数1/Keq的设置可使SOC保持平衡,故权系数的计算是动态规划优化算法的另一个重要环节。 2.3 权系数的计算 传统动态规划算法中的权系数通常依据经验通过反复尝试确定,缺少充分的解释说明和理论依据。本文中权系数1/Keq的确定需要满足SOC平衡的条件,所以权系数的计算等同于求SOC变化量为0的近似解的过程。 ΔSOC=f(Keq) (23) 混合动力系统是非线性的,工况前后SOC变化量与工况油电转换系数Keq的关系难以准确列出,所以求f函数零值近似解考虑采用牛顿迭代法的衍生方法——割线法,它和牛顿迭代法都具有收敛性,但又不需要明确f(Keq)的表达式。 设f(x)在[a,b]上有唯一的零点x*,取x0=a,x1=b,则过P0(x0,f(x0))和P1(x1,f(x1))的割线的方程为 (24) n=1,2,… (25) 应用割线方程中的斜率得到xn迭代公式的方法称为割线法。 那么假设两个工况油电转换系数Keq0和Keq1,通过动态规划算法求解,得到ΔSOC0和ΔSOC1,应用点(Keq0,ΔSOC0)和(Keq1,ΔSOC1)迭代求解。 油电转换系数迭代求解如图6所示。经过4次迭代,|Keq4-Keq3|<0.01,所以判定keq4即为近似解。 2.4 动态规划算法求解 将第4次迭代的工况油电转换系数Keq4代入单步成本函数中,并反向递推求解最优控制变量及系统各信号的变化曲线,如图7和图8所示。 由图可见,并联混合动力客车的SIMULINK模型在中国城市综合工况下,车速跟随良好,发动机与电机的转矩分配合理,换挡既保证了对工作点的调节又不会过于频繁。 图9为SOC及其罚函数值的变化曲线。由图可见,由于SOC罚函数为SOC变化的平方项,SOC接近0.695的过程中罚函数值快速增大,受罚函数值的影响发动机与电机的转矩分配更倾向于驱动并发电维持SOC平衡,而一旦SOC平衡,罚函数值再次变小,转矩分配倾向于电动行驶,这样转矩分配对工况考虑较少,将削弱全局优化效果,影响整车经济性。 表1为动态算法SIMULINK仿真对比。由表可见,由于本文中提出的动态规划优化算法具有更加合理的SOC平衡控制,使百公里油耗约减少1L,整车经济性优化6.06%,但由于动态规划算法求解所建模型是基于一定假设的简化模型,所以还需要在CRUISE中进行仿真验证。 表1 动态规划算法SIMULINK仿真对比 在联合仿真平台验证动态规划算法,首先要将基于时间的最优控制变量提炼为基于需求转矩、车速或转速等多种输入信号的控制规则。 3.1 控制规则的提炼 根据模式切换、换挡和转矩分配3方面控制规则可分为制动换挡规则、驱动模式切换及换挡规则、驱动转矩分配规则。制动工况下尽可能回收再生制动能量,所以只考虑其换挡规则。 图10为制动模式下的换挡规则,其中圆点为1~4挡的电机制动工作点,根据工作点位置可画出1-2挡、2-3挡、3-4挡的换挡曲线。 根据驱动模式切换和换挡的边界工作点,图11提炼了驱动模式间的切换规则和换挡规则,曲线1与坐标轴所围区域为电机单独驱动,曲线2为发动机在各挡位下可输出的最大转矩线,曲线1与2所围区域为发动机和电机同时工作,电机驱动或发电,而超出曲线2区域发动机和电机联合驱动,发动机输出最大转矩。曲线1与2所围区域两个动力源之间的转矩分配如图12所示。 3.2 联合仿真结果对比 根据所提炼的控制规则改进控制策略,并在CRUISE/SIMULINK仿真平台上进行联合仿真。由于CRUISE仿真中发动机参与驱动需要起机和转速同步控制,这与动态规划建模所假设的情况不同,所以影响了所提出算法的优化效果。表2为与传统动态规划算法在中国城市综合工况下的对比结果。由表可见,动态规划优化算法虽然没有完全达到SIMULINK中的效果,但仍然进一步优化了3.23%,整车百公里油耗减少0.55L。 动态规划算法作为全局最优算法中的研究热点,仍然存在着成本函数受SOC变化影响大、权系数确定方法缺乏理论依据等问题。针对以上两个问题,本文中提出了动态规划优化算法,这种算法的核心是以等效油耗为单步成本函数,同时采用割线法迭代计算最优油电转换系数即权系数。在此基础上以并联混合动力客车为研究对象,在SIMULINK中搭建简化模型,并依据成本函数和反向递推公式求取最优控制变量集合,进而提炼基于动态规划优化算法的控制规则。最后根据控制规则改进控制策略在SIMULINK和CRUISE两个仿真平台下与传统动态规划算法进行仿真对比,结果显示中国城市综合工况下动态规划优化算法在两种仿真平台分别提升整车经济性6.06%和3.23%,最多约节约燃油消耗1L。进一步说明本文中所提出的优化算法更为合理可行。 [1] 左义和,项昌乐,等.基于动态规划算法的混联混合动力汽车控制策略[J].吉林大学学报(工学版),2011,41(4):898-903. [2] 申彩英,夏超英.基于改进型动态规划算法的串联混合动力汽车控制策略[J].控制理论与应用,2011,28(3):427-432. [3] 吴迪.ISG混合动力汽车能量优化管理策略研究[D].合肥:合肥工业大学,2013:1-131. [4] 王磊.一种混联式混合动力客车能量管理及模式切换协调控制[D].上海:上海交通大学机械与动力工程学院,2013:1-170. [5] 邹渊,侯仕杰,韩尔樑,等.基于动态规划的混合动力商用车能量管理策略优化[J].汽车工程,2012,34(8):663-668. [6] 林歆悠,孙冬野,等.基于随机动态规划的混联混合动力客车能量管理策略[J].汽车工程,2012,34(9):830-836. [7] 肖仁鑫,李涛,等.基于随机动态规划的混联混合动力汽车能量管理策略[J].汽车工程,2013,35(4):317-321. [8] 李卫民.混合动力汽车控制系统与能量管理策略研究[D].上海:上海交通大学电子信息与电气工程学院,2008:1-122. [9] 舒红,蒋勇,等.中度混合动力模型预测控制策略[J].重庆大学学报,2010,33(1):36-41. [10] 舒红,高银平,等.中度混合动力汽车燃油经济性预测控制研究[J].公路交通科技,2009,26(1):149-153. [11] 欧阳易时,金达锋,罗禹贡.并联混合动力汽车功率分配最优控制及其动态规划性能指标的研究[J].汽车工程,2006,28(2):117-121. [12] 于永涛.混联式混合动力车辆优化设计与控制[D].长春:吉林大学汽车工程学院,2010:1-151. Control Strategy Optimization for a Parallel Hybrid Electric BusBased on Dynamic Programming Algorithm Ba Te, Gao Yinhan, Wang Qingnian, Zeng Xiaohua & Song Dafeng JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130025 Aiming at the problems of the great influence of SOC changes on cost function and the lack of theoretical basis in determining weighting coefficients in traditional dynamic programming algorithm, a dynamic programming optimization algorithm for a parallel hybrid electric bus is proposed in this paper, with the equivalent fuel consumption as cost function and using secant iterative method to calculate weighting coefficients. According to the simplified SIMULINK model constructed with certain assumptions, an optimal control variable set is obtained by using cost function and reverse recursive formula, and effective control rules are refined to improve control strategy. The results of SIMULINK simulation and SIMULINK/CRUISE co-simulation show that with comprehensive driving cycle for Chinese city, the fuel consumption with dynamic programming optimization algorithm is 6.06% and 3.23% less than that with traditional dynamic programming algorithm respectively, demonstrating the better reasonability and energy saving effects of the optimization algorithm proposed. hybrid electric bus; dynamic programming; control rules; algorithm optimization *国家自然科学基金青年基金(51305155)资助。 原稿收到日期为2015年1月12日,修改稿收到日期为2015年8月14日。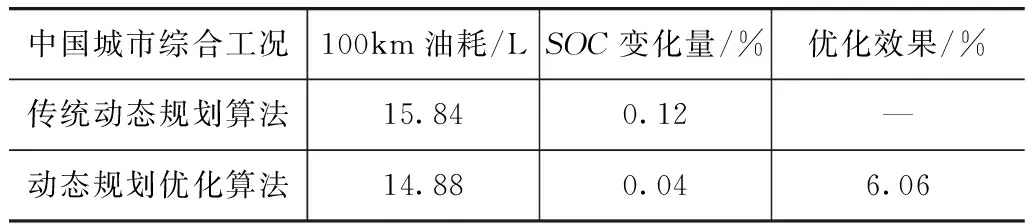
3 CRUISE/SIMULINK联合仿真验证
4 结论
