计及不均匀发热与温度分布的锂离子单电池电化学-热力学耦合三维有限元模型

张立军，李文博，程洪正

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804)



2015233

计及不均匀发热与温度分布的锂离子单电池电化学-热力学耦合三维有限元模型

张立军，李文博，程洪正

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804)

为预测锂离子电池的内部温度场,应用多孔电极理论，建立了锂离子电池的一维电化学生热模型，同时考虑正负极集流板和电解液的欧姆热，与基于温度场相似准则建立的锂离子单电池三维分层模型耦合，组成锂离子单电池温度场有限元模型。基于模型进行1倍率恒流放电工况下的热力学计算，系统考察了电池温度变化与分布特征，并对比分析了各层不均匀发热率分布情况。仿真结果表明，所建立模型能较准确地预测锂离子电池内部分层结构发热分布和温度场，有助于后续的关键影响因素分析。

锂离子电池；电化学；相似准则；温度场；生热

前言

动力电池是电动汽车的核心部件，而锂离子电池因其优异的综合性能倍受关注，并被视为未来极具实用化前景的电动汽车储能方案之一[1-3]。

锂离子动力电池在充放电过程中伴随复杂的化学、电化学反应和物质传输过程，电池反应生热和运行工况、冷却方式等共同影响电池的温度场，进而影响其综合性能。当电池温度分布极不均匀，或温度过高过低时，可能会导致电池损坏乃至安全事故。因此，针对锂离子电池进行热动力学建模，预测内部温度场，进行电池热管理已经成为锂离子电池开发的核心技术[4-7]，意义重大。

目前，采用有限元方法进行电池多物理场的建模与分析已经比较普遍。建模时往往采用不分层的集总参数模型，结合一维电化学模型进行单体锂离子电池的电化学-热耦合分析[8]，或者忽略单电池厚度方向的温度梯度，仅仅预测电池表面温度分布[9-11]。实际上，锂离子电池是三维结构，而且不同部分具有不同的发热机制和发热量，必然存在内部温度场及温度梯度。为了克服电池多层三维结构尺寸的跨尺度困难，作者曾提出了一种基于相似原理的电池多物理场的有限元建模与分析方法[12-13]，但当时假设电池内部为均匀体发热，与实际不相符。

为了对锂离子单电池各结构层的生热分布和内部温度场进行更加精准的预测，本文中在前期基于相似原理建立的温度场有限元模型的基础上，针对某型锂离子电池(正极为磷酸铁锂，负极为碳化锂)，利用一维电化学模型计算电极电化学热，结合电极集流板和电解液的欧姆热，实现了发热模型和相似原理有限元温度场模型的集成，给出了锂离子电池内部温度场的仿真分析方法。本文中的研究工作可为锂离子电池的模块集成和热管理开发提供重要依据。

1 锂离子单电池的建模

1.1 总体建模思路

图1为锂离子电池电化学-热耦合模型的总体框架图。锂离子单电池生热由正、负电极电化学热和正、负集流板(含极耳)、电解液的欧姆热构成。其中，锂离子单电池正、负电极的电化学热与电解液生热可以由一维电化学模型计算得到，正、负集流板的欧姆热和电池的温度场分布可由基于相似性原理建立的三维热模型计算得到。另外，正、负电极电化学热的计算利用正、负电极的平均温度。

1.2 锂离子电池温度场的相似性准则与热平衡

基于相似性原理建立锂离子单电池三维分层模型的方法详见文献[13]，其要点如下。

1.2.1 温度场相似性准则[13]

电池的生热散热过程是一个典型的三维、内热源的非稳态导热过程，可以利用三维常物性、非稳态、第三类边界条件下的导热微分方程进行描述。

控制方程：

(1)

第三类边界条件：

(2)

初始条件：

t=0；T(x,y,z,t)=T0

(3)

式中：λx,λy和λz分别为电池x，y和z方向的导热率；T为温度；Q为单位体积生热率；a，b和c为x，y和z方向长度；ρ为密度；Cp为比热容；t为时间。

为将式(1)～式(3)作无量纲化处理，引入长度、时间和温度3个标尺。

长度标尺取δx，δy和δz，温度标尺取θ,时间标尺取τ,分别为

(4)

无量纲化导热微分方程为

(5)

式中：Θ为无量纲温度;X,Y和Z为无量纲位置坐标；Tref为参考温度；Fo为傅里叶数；表征无量纲时间。

第三类边界条件：

(6)

式中：Θ=θ/θ0

式中：Bix，Biy和Biz为毕渥数，表征无量纲对流散热系数；A，B和C为无量纲对流边界位置。

初值条件：

Fo=0；Θ=1

(7)

由式(5)～式(7)可以看出，无量纲过余温度Θ为Bix，Biy，Biz，Fo，Q′，X，Y，Z，A，B和C的函数。

以上为三维常物性、非稳态、第三类边界条件下非稳态导热问题的相似准则数。

1.2.2 温度场相似关系

基于相似理论提出将厚度方向尺寸放大N倍的温度场相似模型。根据前面的分析，要实现温度场相似，相似准则数必须相等。由此确定相似模型与原型之间的参数必须满足如表1所示的比例关系。当满足表1条件时，模型与原型的温度场相似。

表1 模型参数设置比例关系(原型∶模型)

1.2.3 锂离子单电池热平衡

本文中主要考虑锂离子单电池的3种生热形式：可逆热、极化热和欧姆热[14]。

电池内部能量守恒方程如下：

Q=Qrev+Qirre

(8)

式中： Qrev为可逆热；Qirre为不可逆热。

(9)

式中：Sa,i为比表面积；jloc,i为局部电流源；Ui为开路电压；下标i=n,p,s，分别代表多孔电极负极、多孔电极正极和隔膜，下同。

Qirre=Qact+Qohm

(10)

式中：Qact为极化热，Qohm为欧姆热。

Qact=Sa,ijioc,i(φ1,i-φ2,i-Ui)

(11)

式中：φ1,i为电极固相电势；φ2,i为液相电势。

(12)

(13)

式中：κ1,i为固相锂离子电导率；κ1,eff,i为固相有效锂离子电导率；ε1,i为固相活性物质体积分数；γ1,i为固相布鲁格曼常数；κ2,eff为有效液相锂离子电导率；κ2为液相锂离子电导率；ε2为液相体积分数；γ2为液相布鲁格曼常数；c2为液相中锂离子浓度；Li为正极、负极或隔膜厚度，见图2。

热边界条件为对流热边界，即

(14)

式中：Tabm为环境温度；h 为对流换热系数。

1. 3 电化学模型

本文中基于多孔电极理论，在COMSOL软件的环境下对锂离子电池进行一维电化学建模，一维模型结构如图2所示。

1.3.1 电荷守恒

固相电荷平衡方程式：

Liφ1,i)=-LiSa,ijloc,i

(15)

(16)

其中，φ1在边界1上设置为0；边界4上，电荷流量等于电池的平均电流密度；边界2和3上没有电荷流动，设置为绝缘。

(17)

(18)

液相电荷守恒的控制方程为

(19)

式中：F为法拉第常数；t+为溶液中锂离子的迁移数。

液相接界电势方程为

(20)

式中：ν与电解液活跃度相关，是温度与电解液浓度的导数；f为液相活化系数。

外边界无电流，故在边界2和边界3可以设置如下：

(21)

1.3.2 质量平衡

固相中锂离子在电极活性嵌入颗粒的质量平衡方程，用菲克第二定律描述(假设颗粒为球体)为

(22)

式中：c1,i为固体活性颗粒中锂离子浓度；D1,i为锂离子在固相中的扩散速率；ri为活性颗粒半径。

边界条件为颗粒的中心没有锂离子的流动，颗粒的边界上，由于化学反应产生的锂离子流动为锂离子的嵌入或脱嵌速率。

(23)

液相中质量平衡方程为

(24)

(25)

式中：jloc,i为局部电流源；D2为锂离子在液相中的扩散速率；D2，eff为锂离子在液相中的等效扩散速率。

在边界1和边界4上，液相的传质均为0；在边界2和边界3上其传质是连续的。

1.3.3 电化学反应速度

巴特勒—伏尔摩运动方程：

(26)

式中：j0,i为交换电流；ηi为过电势；jloc,i由过电势决定，过电势是由固相电势与液相电势之差，减去固相的热力学平衡势；j0,i是一个与温度和浓度有关的变量，正负极所对应的方程不同。

ηi=φ1,i-φ2,i-Ui

(27)

其中开路电压Ui由正负极锂离子浓度及参考温度决定：

(28)

式中：Ui,ref为参考温度下的开路电压；Tref为参考温度，此处设为298.15K。

1. 4 模型参数设置

模型固定参数设置分为几何参数设置，电化学参数设置和热特性参数设置，分别如表2～表5所示[13-15]。

表2 单电池各层长度 μm

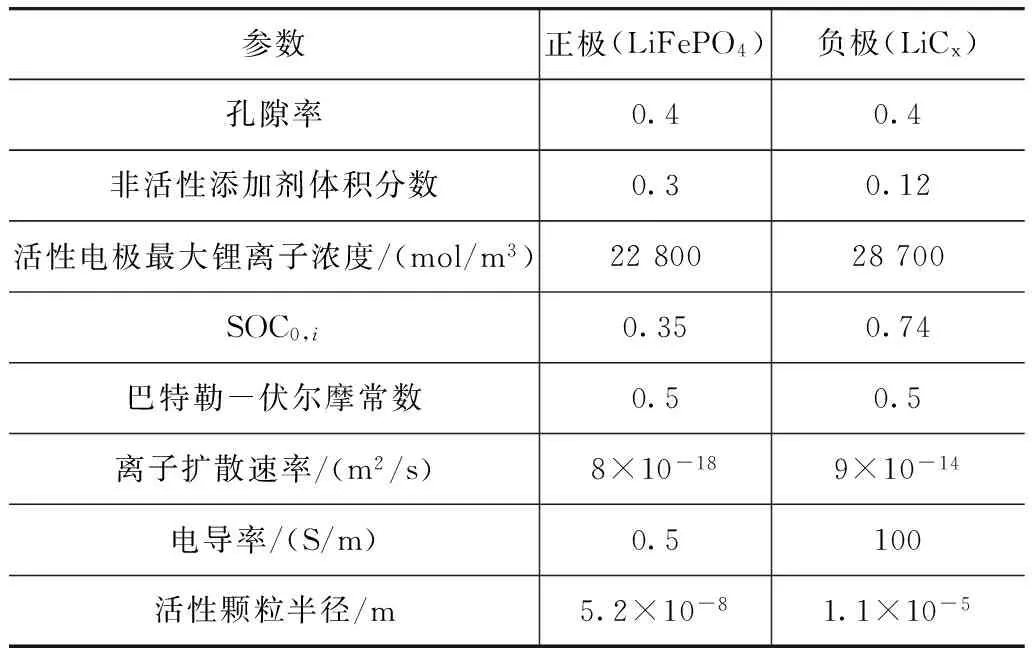
表3 正负多孔极电化学参数

表4 隔膜电化学参数

表5 关于生热传热的参数

模型可变参数设置如下[13,15]：

(1)电解液电导率

(29)

(2)溶液中锂离子传递系数

(30)

(3)活度系数

(31)

(4)交换电流密度

(32)

式中：正极为j0,ref,p=(1.34×10-3)e(-15000/8.314T)；负极为j0,ref,n=20e(-30000/8.314T)；c2为溶液中锂离子浓度；T为温度；cref为溶液中锂离子的参考浓度值为1mol/m3；c1,i,ref取自于各电极SOC为50%时固相颗粒的锂离子浓度。本文中定义“电极SOC”为正极或负极所含的锂离子浓度与对应正极或负极最大锂离子浓度之比：

(33)

式中：c1,max,i为固相颗粒最大锂离子浓度。

(5)磷酸铁锂电池平衡势随SOCi的变化关系

正极平衡势随SOCp的变化关系为

Up,ref=

(34)

负极平衡势随SOCn的变化关系：

Un,ref=

(35)

(6)磷酸铁锂电池熵变化引起的发热变化

正极：

1.9635SOCp5-0.98716SOCp4+0.28857SOCp3-

0.046272SOCp2+0.0032158SOCp-1.1986×10-5

(36)

负极：

0.8520278805SOCn+0.36229929SOCn2+0.2698001697)/1000

(37)

1.5 初始条件与工况设定

初始条件和工况设置如下。

(1)电池运行工况为40A放电，单体电池由154个单电池并联组成，等效到每个单电池的极耳电流为0.259 7A，放电时间设为1 800s。

(2)单电池模型初始参数设置为：初始温度为298.15K；初始电解液浓度为1 000mol/L；负极初始SOC为0.74，正极初始SOC为0.35。

(3)三维焦耳热模型参数按照锂离子电池温度场相似性准则进行设置，在软件中材料设置为各向异性，在Z方向其尺寸扩大了1 000倍，参数设置如表6所示。

表6 基于相似性原理的三维焦耳热模型的传热参数设置[13]

2 仿真结果与分析

2.1 温度特性分析

2.1.1 总体温升特性分析

锂离子电池放电是一个典型的，有时变内热源的瞬态导热过程。图3为锂离子单电池各层平均温度随放电时间的变化。由图3可见，在整个放电过程中，电池的平均温度呈非线性上升。但是，电池平均温度上升并非呈严格的线性上升。这是因为，电池温度的升高会影响发热量的变化。另外，与其它各层相比，正负极极耳处的平均温度稍高。

2.1.2 温度不均匀性分析

图4为锂离子单电池最大温差随放电时间的变化。由图4可见，最大温差随着放电过程进行而增大，但是，到放电结束时最大温差也只有0.3K左右，说明在所仿真的工况下，电池的温度总体上比较均匀。

图5为放电结束时电池温度的总体分布情况。由图5可见：放电结束时，电池中心的温度最高，并由中心向两侧逐渐降低；但在单电池厚度方向上基本不存在温度梯度。

图6为放电结束时电池的各层温度分布情况。由图6可见：(1)温度在各层中心平面分布形态相似；(2)各层最高温度值相同，且基本上都集中在中心偏上的位置，各层最低温度相同，且都集中在左下角；(3)正负极极耳的温度稍高。

2.2 生热特性分析

2.2.1 各层生热特性分析

锂离子电池各层生热与温度场的分布有着极为密切的联系。图7所示为各层平均生热速率随放电时间的变化。由图7可知，各层平均生热速率存在很大的差别：(1)负极平均生热速率变化程度最大，且随着放电过程的进行，其平均生热速率逐渐增大；(2)正极平均生热速率随放电时间增加而缓慢上升，变化较小；(3)由于是恒电流放电，正负集流板欧姆热与溶液欧姆热基本保持不变。

图8和图9分别为放电结束时正负极集流板生热速率和电流密度分布情况。从图8和图9可以看出，极耳处存在发热集中，这是因为极耳处的电流密度最大。

2.2.2 不同生热机理生热特性分析

图10所示为正负极可逆热与不可逆热随时间的变化历程。由图可得如下结果。

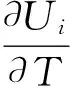
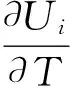
3 结论

本文中建立锂离子单电池一维电化学和基于相似原理的三维热耦合模型，并进行仿真分析，主要得到以下结论。

(1)应用一维电化学模型和基于锂离子单电池相似准则的三维温度场模型耦合建立的电化学热耦合模型进行锂离子单电池的温升特性与生热特性分析是可行的；

(2)在恒流放电工况下，单电池厚度方向上温度较为一致，但平面方向的温度由中心向边缘逐渐降低，且极耳处存在热集中；

(3)放电过程中各层平均温度和平均生热速率均呈上升趋势，且放电后期负极生热，尤其是负极的可逆热占主导地位。

本文的研究为进行复杂工况下的温度场计算与评价和指导多电池组成的电池单体和电池模块的热力学特性计算提供新的方法，但模型参数和预测精确性仍需要在后续的电池试验中予以检验。

[1] Song L, Li X, Wang Z, et al. Thermo-Electrochemical Study on the Heat Effects of LiFePO4Lithium-ion Battery During Charge-Discharge Process[J]. International Journal of Electrochemical Science, 2012, 7(8).

[2] Guo G, Long B, Cheng B, et al. Three-Dimensional Thermal Finite Element Modeling of Lithium-ion Battery in Thermal Abuse Application[J]. Journal of Power Sources, 2010, 195(8): 2393-2398.

[3] Doyle M, Fuller T F, Newman J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.

[4] 宋丽, 魏学哲, 戴海峰, 等. 锂离子电池单体热模型研究动态[J]. 汽车工程, 2013，35(3): 285-291.

[5] Wu M S, Liu K H, Wang Y Y, et al. Heat Dissipation Design for Lithium-ion Batteries[J]. Journal of Power Sources, 2002, 109(1): 160-166.

[6] 彭强.电动车用锂离子电池热效应研究[D].长春：吉林大学，2012.

[7] 李腾，林成涛，陈全世.锂离子电池热模型研究进展[J].电源技术，2009，33(10)：927-932.

[8] Kim G H, Smith K, Lee K J, et al. Multi-Domain Modeling of Lithium-ion Batteries Encompassing Multi-Physics in Varied Length Scales[J]. Journal of The Electrochemical Society, 2011, 158(8): A955-A969.

[9] Guo M, White R E. A Distributed Thermal Model for a Li-ion Electrode Plate Pair[J]. Journal of Power Sources, 2013, 221: 334-344.

[10] Kim U S, Yi J, Shin C B, et al. Modeling the Dependence of the Discharge Behavior of a Lithium-ion Battery on the Environmental Temperature[J]. Journal of The Electrochemical Society, 2011, 158(5): A611-A618.

[11] Kim U S, Shin C B, Kim C S. Modeling for the Scale-up of a Lithium-ion Polymer Battery[J]. Journal of Power Sources, 2009, 189(1): 841-846.

[12] 程洪正, 张立军, 阮丞, 等. 锂离子电池应力应变场的相似准则推导与有限元验证[J]. 中国科学: 技术科学, 2013 (6): 670-683.

[13] 程洪正, 张立军, 阮丞, 等. 锂离子电池温度场相似准则推导与有限元验证[J]. 同济大学学报(自然科学版), 2013, 41(8).

[14] Ye Y, Shi Y, Cai N, et al. Electro-Thermal Modeling and Experimental Validation for Lithium-ion Battery[J]. Journal of Power Sources, 2012, 199: 227-238.

[15] Gerver R E, Meyers J P. Three-Dimensional modeling of Electrochemical Performance and Heat Generation of Lithium-ion Batteries in Tabbed Planar Configurations[J]. Journal of The Electrochemical Society, 2011, 158(7): A835-A843.

Coupled Thermodynamic-Electrochemical 3D FE Model for Single Lithium-ion Battery with Consideration of Uneven Heat Generation and Temperature Distribution

Zhang Lijun,Li Wenbo & Cheng Hongzheng

1.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804;2.NewCleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804

For predicting the internal temperature field of lithium-ion battery, an one-dimensional electrochemical heat gereration model for a single lithium-ion battery is built by applying porous electrode theory, with concurrent consideration on the ohmic heat generation of cathode and anode current collectors and electrolyte, and coupled with a three-dimensional layered model based on temperature field similarity criterion to compose a temperture field FE model for lithium-ion battery. Based on the model a thermodynamics calculation in 1C discharge condition is conducted, the variation and distribution features of battery temperature is investigated, and the distribution of uneven heat generation rate in each layer is comparatively analyzed. The results of simulation show that the model built can rather acccurately predict the heat generation distribution and temperature field of internal layered structure of lithium-ion battery, inducive to subsequent key influencing factor analysis.

lithium-ion battery; electrochemistry; similarity criterion; temperature field; heat generation

*国家973 计划项目( 2011CB711201) 资助。

原稿收到日期为2014年3月24日，修改稿收到日期为2014年7月4日。