关于Diophantine方程x3-1=91y2
2015-06-09钱立凯普粉丽
钱立凯,普粉丽
(1.曲靖师范学院教师教育学院,云南曲靖655011;2.普洱学院数学与统计学院,云南普洱665000)
关于Diophantine方程x3-1=91y2
钱立凯1,普粉丽2
(1.曲靖师范学院教师教育学院,云南曲靖655011;2.普洱学院数学与统计学院,云南普洱665000)
利用初等方法证明了Diophantine方程x3-1=91y2仅有整数解(x,y)=(1,0)。
Diophantine方程;整数解;同余式;平方剩余;Legendre符号;递归序列
关于方程x3-1=Dy2(D>0是非平方数)是一类重要的三次Diophantine方程,其整数解已有不少人研究过。当D不含6k+1形素因子时,文[1]证明了当D>2,D无平方因子且不含3及6k+1形素因子时,方程x3-1=Dy2无非平凡解;文[2]证明了当D>2,D无平方因子且不含6k+1形素因子时,方程x3-1=Dy2无非平凡解。但当D含6k+1形素因子时,方程的非平凡解的求解较为困难,文[3]给出了当0 定理 Diophantine方程 x3-1=91y2 (1) 仅有整数解(x,y)=(1,0)。 引理1[5]方程4x4-3y2=1仅有整数解(x,y)=(±1,±1)。 引理2[6]方程x4-3y2=1仅有整数解(x,y)=(±1,0)。 引理3[5]方程x2-3y4=1仅有整数解(x,y)=(±2,±1),(±7,±2),(±1,0)。 证明:因为(x-1,x2+x+1)=(x-1,(x-1)2+3(x-1)+3)=(x-1,3)=1或3,故Diophantine方程(1)给出以下8种分解: 情形(Ⅰ)x-1=13u2,x2+x+1=7v2,y=uv,(u,v)=1 情形(Ⅱ)x-1=7u2,x2+x+1=13v2,y=uv,(u,v)=1 情形(Ⅲ)x-1=u2,x2+x+1=91v2,y=uv,(u,v)=1 情形(Ⅳ)x-1=91u2,x2+x+1=v2,y=uv,(u,v)=1 情形(Ⅴ)x-1=39u2,x2+x+1=21v2,y=3uv,(u,v)=1 情形(Ⅵ)x-1=21u2,x2+x+1=39v2,y=3uv,(u,v)=1 情形(Ⅶ)x-1=3u2,x2+x+1=273v2,y=3uv,(u,v)=1 情形(Ⅷ)x-1=273u2,x2+x+1=3v2,y=3uv,(u,v)=1 备注:文中用符号(u,v)表示整数u,v的最大公约数,其中u,v∈Z。 情形(Ⅰ)将x-1=13u2代入x2+x+1=7v2,得(26u2+3)2+3=7(2v)2,即 (26u2+3)2-7(2v)2=-3 (2) 因为方程X2-7Y2=-3由两个结合类得到,其基本解为(5,2),而Pell方程X2-7Y2=1的基本解为(8,3),故(2)式的全部整数解由以下两个结合类给出: 26u2=±xn-3 (3) 由式(3)得xn≡±(mod 26)。 容易验证下式成立: xn+2=16xn+1-xn,x0=5,x1=82 (4) 对递归数列(4)取模26,其剩余类周期为14,且xn≢±3(mod 26)。所以(3)式不成立。故该情形Diophantine方程(1)无整数解。 情形(Ⅱ) 由x-1=7u2知x=7u2+1,从而x≡0,1,5(mod 8),则x2+x+1≡1,3,7(mod 8)。而v为奇数,故v2≡1(mod 8),则13v2≡5(mod 8),这与x2+x+1=13v2矛盾,故该情形Diophantine方程(1)无整数解。 情形(Ⅲ) 将x-1=u2代入x2+x+1=91v2,得(2u2+3)2+3=91(2v)2,则有(2u2+3)2+3≡ 情形(Ⅳ) 解x2+x+1=v2,得x=0,-1,均不适合第一式,故该情形Diophantine方程(1)无整数解。 情形(Ⅴ) 由x-1=39u2知x=39u2+1,从而x≡0,1,5(mod8),则x2+x+1≡1,3,7(mod8)。而v为奇数,故v2≡1(mod8),则21v2≡5(mod8),这与x2+x+1=21v2矛盾,故该情形Diophantine方程(1)无整数解。 情形(Ⅵ) 将x-1=21u2代入x2+x+1=39v2,得(42u2+3)2+3=39(2v)2,即 (42u2+3)2-39(2v)2=-3 (5) 因为方程X2-39Y2=-3由一个结合类得到,其基本解为(6,1),而Pell方程X2-39Y2=1的基本解为(25,4),故方程(5)的全部整数解可表示为: 因此X2-39Y2=-3不存在满足2|Y的整数解,故方程(5)无整数解,所以该情形Diophantine方程(1)无整数解。 情形(Ⅶ) 由x-1=3u2知x=3u2+1,从而x≡1,4,5(mod8),则x2+x+1≡3,5,7(mod8)。而v为奇数,故v2≡1(mod8),则273v2≡1(mod8),这与x2+x+1=273v2矛盾,故该情形Diophantine方程(1)无整数解。 情形(Ⅷ) 将x-1=273u2代入x2+x+1=3v2,得(546u2+3)2+3=3(2v)2,即 (2v)2-3(182u2+1)2=1 (6) 因为Pell方程X2-3Y2=1的基本解为(2,1),因此方程(6)的一切整数解可表示为: 因此有182u2+1=±yn(n∈Z),即182u2=±yn-1。又y-n=-yn,所以只需考虑: 182u2=yn-1 (7) 由(7)得 yn≡1(mod2) (8) 容易验证下列各式成立: yn+2=4yn+1-yn,y0=0,y1=1 (9) yn+1=xn+2yn,xn+1=2xn+3yn (10) (11) (12) y2n=2xnxn (13) 对递归序列(9)取模2,得周期为2的剩余类序列,且仅当n≡1(mod2)时yn≡1(mod2),故(8)要成立,需n≡1(mod2)。 对递归数列(9)取模7,其剩余类周期为8,当n≡5,7(mod8)时,有yn≡6(mod7),则有0≡182u2=yn-1≡5(mod7),矛盾,故(7)式不成立。 对递归数列(9)取模13,其剩余类周期为12,当n≡3,7,9,11(mod12)时,有yn≡2,12,11,12(mod13),则有0≡182u2=yn-1≡1,10,11(mod13),矛盾,故(7)式不成立。从而n≡1(mod8)。 91u2=x4m+1y4m (14) 又对递归序列取模7,得周期为8的剩余类序列:1,4,1,0,6,3,6,0,…,当n≡0,4(mod8)时,有yn≡0(mod7),则y4m≡0(mod7)。 由式(10),得(x4m+1,y4m)=(2x4m+3y4m,y4m)=(2x4m,y4m)=2,故(14)可以分解为以下两种情形: x4m+1=2a2,y4m=182b2,u=2ab (15) 或x4m+1=26a2,y4m=14b2,u=2ab (16) 由(16)的y4m=14b2得2x2my2m=14b2,即x2my2m=7b2,则有 x2m=c2,y2m=7d2,b=cd (17) 或x2m=7c2,y2m=d2,b=cd (18) (7c2)2-3d4=1 (19) 由引理3知(19)仅有整数解(c,d)=(±1,±2),所以d=±2,则y2m=4,即m=1,此时n=9,所以由(7),得182u2=y9-1=40544,即13u2=2896,显然无解。故该情形Diophantine方程(1)无整数解。 综上有,Diophantine方程(1)仅有整数解(x,y)=(1,0)。 [1]柯召,孙琦.关于丢番图方程x3±1=Dy2[J].中国科学,1981,24(12):1453-1457. [2]柯召,孙琦.关于丢番图方程x3±1=3DY2[J].四川大学学报,1981,18(2):1-5. [3]倪谷炎.关于丢番图方程x3=Dy2+1[J].国防科技大学学报(自然科学版),1999,21(5):109-111. [4]罗明,黄勇庆.关于不定方程x3-1=26y2[J].西南大学学报(自然科学版),2007,29(6):5-7. [5]曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989:188-189. [6]柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,2011,3:64. [责任编辑 毕 伟] On the Diophantine Equationx3-1=91y2 QIAN Li-kai1,PU Fen-li2 (1.College of Teacher Education,Qujing Normal University,Qujing 655011,China; Using the elementary methods,it was proved that the Diophantine equationx3-1=91y2has only trivial solution. Diophantine equation; integer solution; congruence; quadratic remainder; Legendre symbol; recurrent sequence 2014-11-26 云南省教育厅科研基金(2014Y462) 钱立凯(1982—),男,云南洱源人,曲靖师范学院讲师。 O156 A 1004-602X(2015)02-0051-031 相关引理
2 定理证明
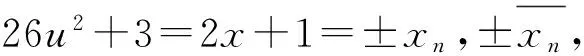
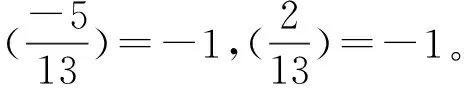
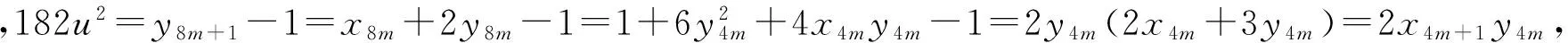
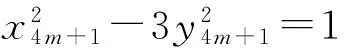
2.College of Mathematics and statistics,Puer University,Puer 665000,China)
