M-矩阵Hadamard积的新下界

蒋建新，李艳艳

(文山学院数学学院，云南文山663000)

M-矩阵Hadamard积的新下界

蒋建新，李艳艳

(文山学院数学学院，云南文山663000)

利用r次Hadamard幂与柯西-施瓦茨不等式，给出了M-矩阵A与非奇异M矩阵B的逆矩阵B-1的Hadamard积的最小特征值q(A∘B-1)的新下界。数值算例说明新的估计式提高了现有的结果。

M-矩阵；Hadamard积；最小特征值；Hadamard幂；下界

1 预备知识

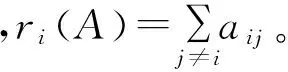
设A=(aij)∈Rn×n，1)如果aij≥0，称A为非负矩阵(A≥0)；2)如果aij≤0，i≠j，称A为Z矩阵，进一步若A-1≥0，就称A为非奇异M矩阵，用Mn表示该类矩阵的集合。q(A)表示非奇异M矩阵A的最小特征值。

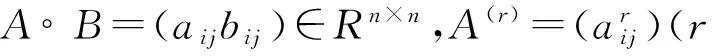
若A，B∈Mn，Fiedler M[1]1991年证明了A∘B-1∈Mn。

引理1[2]设a=(a1，a2，…，an)r≥0，b=(b1,b2,…,bn)T≥0，则有

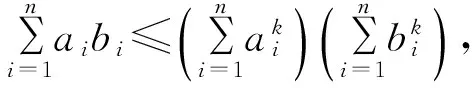
引理2[3]设A=(aij)∈Rn×n是严格对角占优的M-矩阵，则

下面给出迭代矩阵的定义[4]：

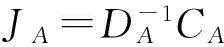
2 主要结果

这部分给出q(A∘B-1)新的下界。

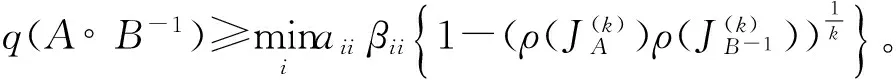
证明：下面分别证明A∘B-1不可约与可约

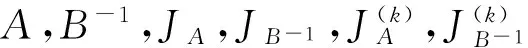
设U=diag(u1，u2，…，un)，V=diag(v1,v2，…，vn)，W=UV=diag(u1v1,u2v2，…，unvn)，则

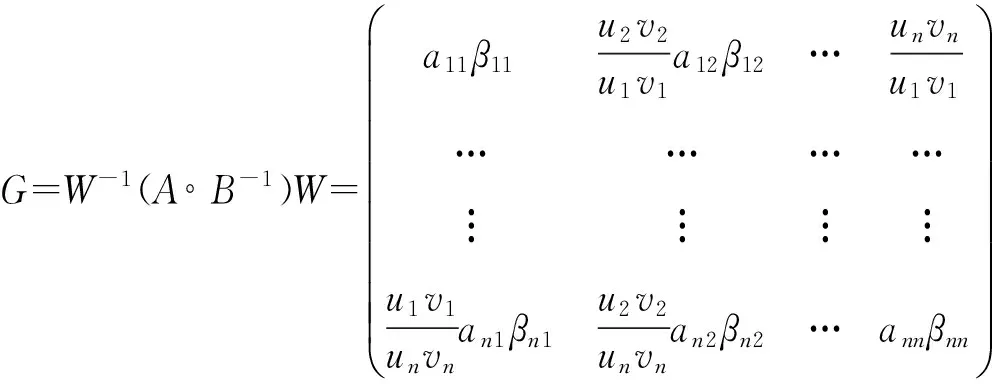
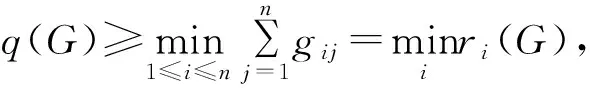
对ri(G)应用引理1得

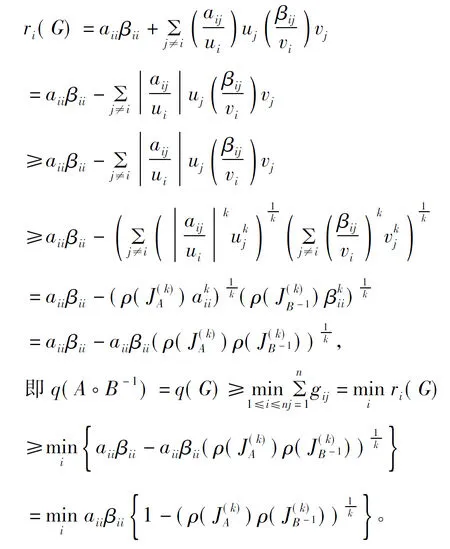
上式对k=1，2成立。

2.若A∘B-1可约，这种情况的证明与文献[5]的证明类似。

当定理1中的B-1=A-1时，可得下面的推论：

推论1A=(aij)∈Rn×n是严格对角占优的M-矩阵，则A-1=(αij)∈Rn×n≥0，且

3 数值算例

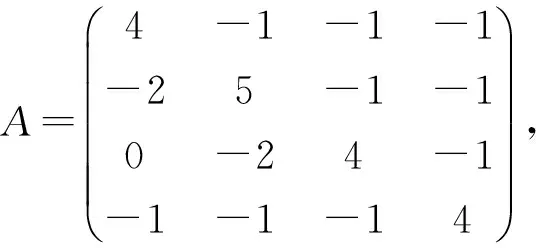
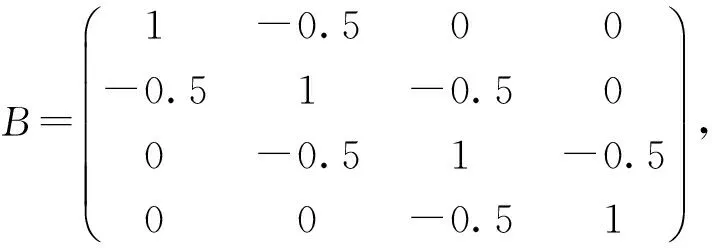
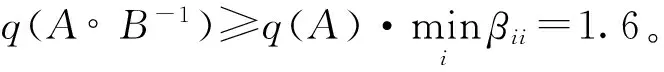
应用2004年陈省生[7]的结果

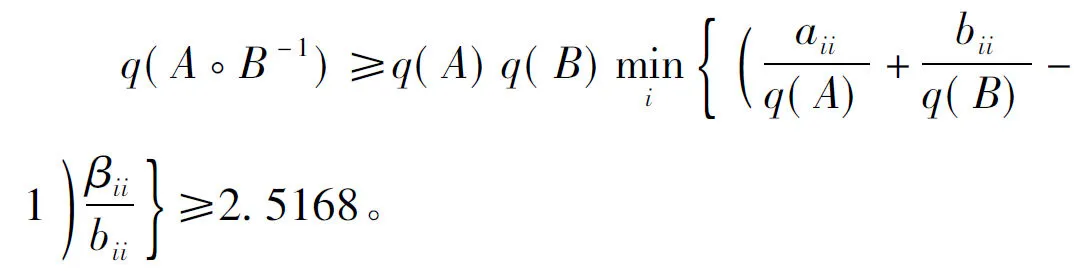
应用本文结果当k=2时，q(A∘B-1)≥2.6515；当k=1时，q(A∘B-1)≥-0.1478。

对于q(A∘A-1)的估计，当k=2时，q(A∘A-1)≥0.3025，事实上q(A∘A-1)=0.3367。

[1]Shivakumar P N,Williams J J,Ye Q,et al.On two-sided bounds related to weakly diagonally dominantM-matrices with application to digital circuit dynamics[J]. SIAMJ Matrix Anal Appl.,1996,17(2):298-312.

[2]杜琨.矩阵Hadamard积和Fan积的特征值的界[J].华东师范大学学报，2008,24(5)：45-50.

[3]Fiedler M and Markham T.An inequality for the Hadamard product of anM-matrix and inverseM-matrix[J]. Linear Algebra Appl,1988,101:1-8.

[4]陈景良，陈向晖. 特殊矩阵[M]. 北京：清华大学出版社，2000：239-276.

[5]HUANG Rong. Some inequalities for the Hadamard product and the Fan product of matrices[J]. Linear Algebra and its Applications,2008,428:1551-1559.

[6]Horn R A,Johnson C R. Topics in Matrix Analysis[M].New York:Cambridge University Press,1991.

[7]CHENG Xing-sheng. A Lower bound for the minimum eigenvalue of the Hadamard product of matrix[J]. Linear Algebra Appl,2004,378:159-166.

[责任编辑 毕 伟]

2014-12-22

云南省教育厅科学研究基金项目(No.2013Y585)；文山学院重点学科数学建设项目(No.12WSXK01)

蒋建新(1981—)，男，甘肃天水人，文山学院讲师。

O151.21

A

1004-602X(2015)02-0054-02