用“小资源”做“大文章”
2015-06-08王金花
王金花

教学应该以人为本,关注学生、关注过程、关注发展。以教材为载体,灵活有效地组织教学,拓展课堂教学空间,力求提高课堂教学的有效性。我们平时关注更多的可能是教材中的例题教学,其实教材中的习题、思考题,还有“你知道吗”这些内容也应予以关注并发挥它们应有的作用。
苏教版小学数学修订版五年级上册第二单元内容是《多边形的面积》,在学习了《三角形的面积计算》后,教材安排了相关的练习,当中有这样两组习题(第12页第10题):
25×12÷2 122×8÷2
25×(12÷2) 122×(8÷2)
笔者让学生先观察每一组两个算式有什么特点,学生说每一组的第二题比第一题多了小括号,其他都一样。我又让学生猜猜每组的两题结果是否相等,有说相等的,有说不等的。接下来,学生通过分组计算发现每一组的两题计算结果均相等,那么以后碰到先乘后除的两步算式,是不是都可以先算后面的除法呢?请学生每个人举一个这样的例子,在四人小组里说一说。最后大家达成共识,凡是此种乘除混合乘法在前的算式,如果计算简便的话都可以先算后面的除法。
到这儿,这个练习似乎可以画上句号了,但是编者的意图到底是什么?难道仅仅是为了计算而计算?我请学生联系三角形的面积计算公式S=a×h÷2思考,能给你带来什么启发吗?学生小越提出在计算时可以先算h÷2。我随即举例,一个三角形的底是30厘米,高是46厘米,三角形的面积是多少平方厘米?学生尝试列式计算:
30×46÷2
=30×(46÷2)
=30×23
=690(平方厘米)
相比于先算30×46显然简便了一些。
接着我又举一例,一个三角形底是40厘米,高是35厘米,三角形的面积是多少平方厘米?学生列式计算:
40×35÷2
=1400÷2
=700(平方厘米)
“怎么不按刚才的方法算了?”
生答:“35除以2有余数。”
“还有别的计算方法吗?”我问。
小思同学站起来说:“老师,我刚刚算了一下,如果先算40÷2=20,再用20×35也是等于700平方厘米。”我把她说的算法也板书在黑板上:
40×35÷2
=40÷2×35
=20×35
=700(平方厘米)
“高先除以2行不通,是不是可以先用底除以2呢?事实证明,可以(同级运算的交换律)。”我肯定了该生的想法,表扬她是个善于思考的孩子。
在进行这个环节的小结时,学生们纷纷说了自己的收获:计算三角形面积时,可以先算底乘高再除以2,可以先用高除以2再与底相乘,也可以先用底除以2再与高相乘。
孩子们似乎明白了在计算三角形的面积时,可以根据数据的特点合理地安排计算的顺序。可是,我总觉得还缺了点什么,尽管学生并没有提出疑问。将三角形面积计算公式中的运算顺序进行调整,除了从表面上看到的得数相同之外,还有什么更有力的支撑吗?
笔者当即想到教材第10页的“你知道吗”,这一内容在上节课研究三角形面积计算时没有也并不适合拿出来讨论。而现在是三角形面积计算的练习课,学生对前一节课的知识已经有所掌握,此时介绍“你知道吗”应该跟这两组计算题的教学目的相辅相成。
另外,笔者在进行单元备课时就想过,除了教材介绍的转化方法,还可以在适当的时候跟学生介绍一些别的转化方法,比如,只用一个三角形或梯形,将其转化成平行四边形来计算面积。这也正好与教材第27页的思考题要求相符,现在或许是个适当的时候。
在心里飞快地权衡了一下,决定临时改变下面的练习计划。笔者让学生自己先用心阅读“你知道吗”的内容,这部分内容图文并茂,主要是理解“半广以乘正从”的意思。学生读完后让大家谈谈对这句话的理解,发现很多孩子都是就字面意思来理解,即用“三角形底的一半乘高”,当再追问为什么是底的一半乘高呢?只有极个别学生能借助教材中的图形解释清楚。
我在黑板上画了一个三角形,问大家:“老师画的三角形与书上的有什么不一样?”学生很快回答,书上的三角形是个等腰三角形,黑板上画的是一个一般三角形。“我们现在用一个一般三角形,按照书上的方法试一试,看看能不能得到三角形的面积计算公式。”其实,我是特意画了一个一般三角形,意在告诉学生任何一个三角形都能用这种方法转化成平行四边形。
接下来我带领学生在黑板上一边画图一边感受着古代数学家们的智慧。
如图,取三角形任意两条边的中点A、B(本想把图中每个顶点都标上字母,怕学生眼花缭乱,所以只标出两个中点),从两个中点出发分别向底边作垂直线段,将左边的直角三角形绕A点顺时针旋转180度,将右边的直角三角形绕B点逆时针旋转180度,就把三角形转化成了一个长方形。长方形的长相当于原来三角形的高,也就是“从”;长方形的宽相当于原来三角形底的一半,因为原来三角形的底分开后变成长方形的两条宽,一条宽就是三角形底的一半,也就是“半广”。长方形的面积=长×宽,所以三角形的面积=底÷2×高。
学生理解了“半广以乘正从”的意思,也真正认同了计算三角形的面积时可以先算底除以2。那么,计算三角形的面积时先算高除以2又有什么道理在其中呢?我让学生自己先动手试一试。
正好上一节课研究三角形面积计算公式时学生那儿都准备了一些三角形,这会儿都拿出来动手剪也好拼也罢,目标是把它转化成平行四边形。孩子们先自己摸索着,一会儿有人主动跟周围的人进行了小声的讨论。汇报时,有学生想到沿着三角形的高把它剪成两个三角形,把其中一个反转以后平移,认为拼成了一个平行四边形。但很快被同学否定了,因为那只是一个一般四边形。我故意若有所思地自言自语:“这种方法倒也不是完全行不通。”学生小梁答道:“如果是等腰三角形或者等边三角形沿着高剪开能拼成平行四边形。”“等腰三角形只能沿着底边上的高剪开哦。”我又补充道。
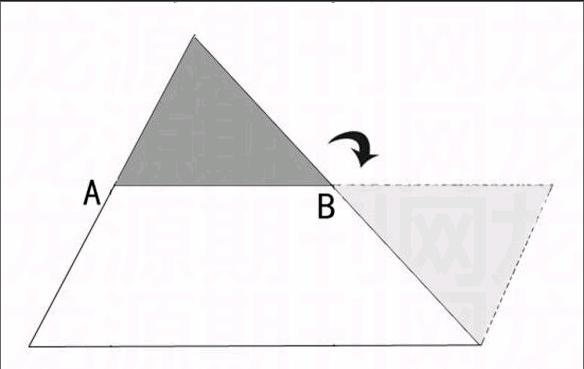
见学生打不开思路,我在黑板上画了一个三角形,并且找出了任意两条边的中点,连成一条线段。学生思考后终于想到了方法。如下图:
连接三角形任意两条边的中点A和B,将上面的小三角形绕B点顺时针旋转180度,或者将小三角形绕A点逆时针旋转180度,就能把三角形转化成一个平行四边形(详细论证,到中学再解决)。当然,把下面的梯形旋转到三角形的旁边也是一样的结果。平行四边形的底相当于原来三角形的底,平行四边形的高相当于原来三角形高的一半,由此得出,三角形的面积=底×(高÷2)。
这样,黑板上出现了三个公式:三角形的面积=底×高÷2,三角形的面积=底÷2×高,三角形的面积=底×(高÷2)。学生观察、比较、交流、小结,这三个公式本质上是一样的,都是用转化的方法得到公式,都用底乘高除以2,只不过考虑谁先除以2,考验大家计算的灵活性,提高计算的正确率。
这节课,学生们都感受到了一种挑战,也有了“原来还可以这样”的收获。“教材无非是个例子”,但用好教材却真的不易,哪怕是一道小小的练习,一篇短短的“你知道吗”。我们应该充分利用这些“小资源”,让学生不断挑战思维,增强思维的宽度与深度,并强化比对沟通,体验点滴成功,从而使他们一点点做好探究数学、爱上数学的“大文章”。
(责任编辑:李雪虹)
