跨阶数的概念及其应用
2015-06-07孙建新
孙建新
(绍兴文理学院 数学系,浙江 绍兴 312000)
跨阶数的概念及其应用
孙建新
(绍兴文理学院 数学系,浙江 绍兴 312000)


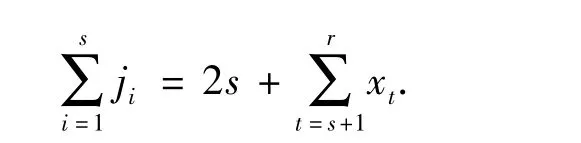
注意到
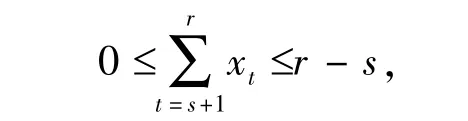
所以
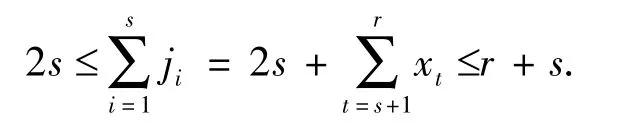
即s>1时(12)式也成立.
若记r阶正则幂指数序列的集合为Jr,则有如下
引理4.3 r阶正则幂指数序列恰有2r-1个.即则|Jr|=2r-1.
证明 对r用数学归纳法证之.
当r=1时,因为1阶正则幂指数序列仅有1个,即J1={2},所以命题为真;
假设1≤r<m时命题为真,即|Jr|=2r-1(1≤r<m).要证r=m时命题亦真.
事实上,在r=m时,有2≤j1≤m+1.由ja取值的不同,可分为m种情况.其中当j1=m+1时,仅有1种:(m+1)11…1;当j1=s(2≤s≤m)时,必有j1=j2=… =js-1=1而jsjs+1…jm根据归纳假设应有2m-s个元素.于是在r=m时,共有元素为
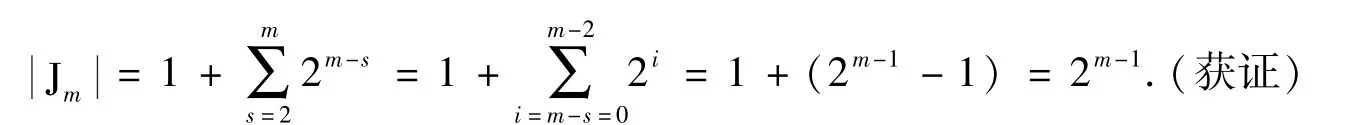
由引理4.1、4.2与4.3,不难写出任何r阶的2r-1个幂指数序列,其低阶的幂指数序列举例如下:

定理4.4 设cr为引理2.2中的系数,则

证明 对下标r用数学归纳法证之.
注意到c0=1,由引理3.1可得可知命题对r≤2成立.
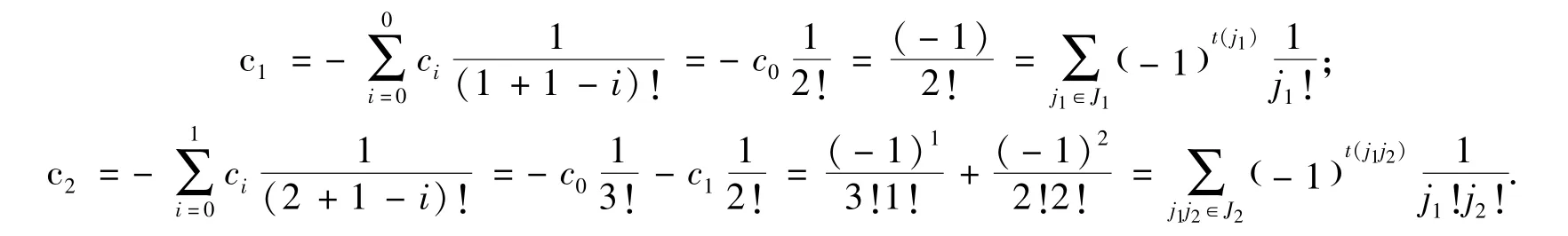
假设命题对r<m成立,要证明r=m时也成立.
事实上,若j1+j2+… +jr=2m,由引理4.1可设s=j1≥2,则有j2=… =js-1=1,js≥2.所以j1+j2+…js-1=s+(s-2)=2s-2,由此可得js+js+1+… +jm=2(m-s+1),(s>1).即jsjs+1…jm∈ Jm-s+1.
由引理3.1以及归纳假设可得
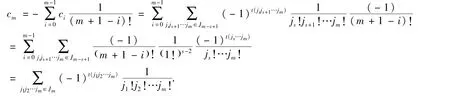
其中,j1=m+1-i≥2(0≤i≤m-1),j2=j3=… =js-1=1.(获证)
5 堆垒级数部分和Sk的展开式系数bk,j的新计算公式
定理5.1 设bk,j为k-1阶堆垒级数部分和Sk-1的关于n的展开式的系数,则

证明 由引理2.1、2.2与2.3可得
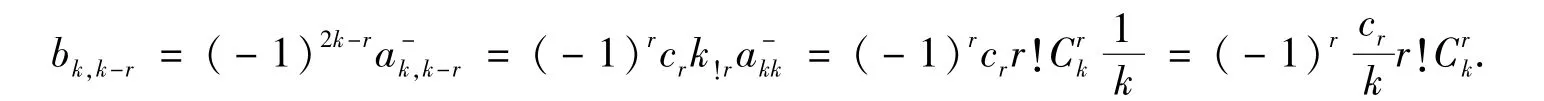
定理5.2 Sk-1的关于n的展开式(14)的系数bkj(j=k-r)的直接计算公式为
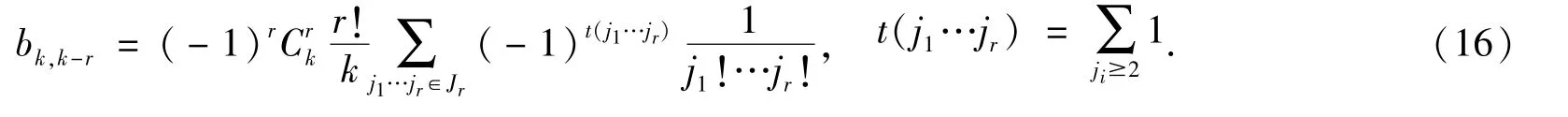
证明 由定理5.1以及定理4.4即得.
由定理5.2,取r=0,1…,7,即得如下推论:
推论5.3 (1) bk,k=1/k(k≥1);
(2) bk,k-1=1/2(k≥2);
(3) bk,k-2=(k-1)/12(k≥3);
(4) bk,k-3=0(k≥4,b4,1=0);
(5) bk,k-4=-(k-1)!3/720(k≥5);
(6) bk,k-5=0(k≥6,b6,1=0);
(7) bk,k-6=(k-1)!5/30240(k≥7);
(8) bk,k-7=-(k-1)!6/30240(k≥8).
[1]孙建新.堆垒级数部分和的一般公式[J].绍兴文理学院学报,2010,30(7):21-25.
[2]孙建新.关于堆垒级数部分和公式的注记[J].绍兴文理学院学报,2011,31(7):1-5.
[3]方开泰.有限差算子及其应用[J].应用数学与计算数学,1984(4):22-31.
(责任编辑 鲁越青)
The Concept of Poly-step Number and Its Application
Sun Jianxin
(Department of Mathematics,Shaoxing University,Shaoxing,Zhejiang 312000)
The new concept,poly-step number,is introduced and applied in the research of the partial sum of stacking series.Then more properties and computational formulas of c r and b kj are obtained.
regular sequence of power exponents;poly-step number;stacking series;partial sum;coefficient of expansion;computational formula
