关于一Qi型积分不等式指数推广

2015-06-07倪仁兴陈厘蒙

绍兴文理学院学报(自然科学版) 2015年1期

关键词：数学系文理学院正整数

倪仁兴陈厘蒙李矗陈辉

(绍兴文理学院数学系,浙江绍兴312000)

关于一Qi型积分不等式指数推广

倪仁兴陈厘蒙李矗陈辉

(绍兴文理学院数学系,浙江绍兴312000)

利用格玛函数和柯西中值定理建立了一Qi型积分不等式的指数推广的两结果,将此Qi型积分不等式的成立范围由正整数拓广至正实数,这从另一角度肯定地回答了2000年F.Qi教授提出的一开问题.另外还修正了2006年Chen和Kimball为回答F.Qi教授开问题所得的一个结果.

格玛函数;柯西中值定理;积分不等式;指数推广;开问题

1 引言与预备

2000年,Feng Qi[1]证得了如下一令人非常感兴趣的积分不等式,即下列定理1:

定理1[1]设f(x)在 a,b[ ]上连续,在(a,b)上可微且f(a)=0.若对x∈(a,b)有f′(x)≥1,则;若对x∈(a,b)有0≤f′(x)≤1,则

同时,Feng Qi将上述定理1的结果从一阶可微拓展到n阶可微的情况,其相应的结论也成立,有如下定理2:

定理2[1]设n是正整数,f(x)在 a,b[ ]上有n阶连续导数,若f(i)(a)≥0(0≤i≤n-1,i∈N+)且f(n)(x)≥n!,则

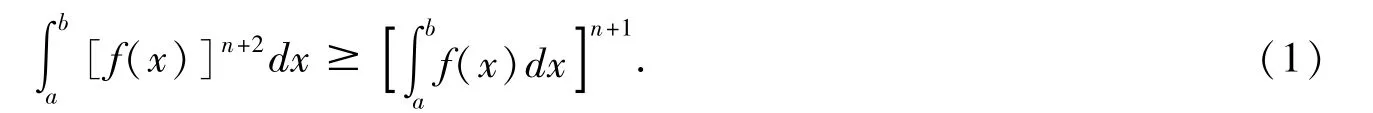
受定理2的启发,自然地,2000年Feng Qi提出了如下一开问题:在什么条件下,将(1)中的正整数n用正实数p来代替,结论仍成立?

许多学者从不同角度对Feng Qi提出的上开问题试图进行回答,如[2～9]等.2006年,Chen和Kimball[2]在上述文献的基础上给出了Feng Qi提出的上述开问题一个回答,得到了如下定理3.

定理3[2]设p是正实数,f(x)在 a,b[ ]上连续,在(a,b)上可微,且f(a)=0,若对x∈(a,b)时有,则

On the Exponential Generalization of Qi type Integral Inequality

Ni Renxing Chen Limeng Li Chu Chen Fai

(Department of Mathematics,Shaoxing University,Shaoxing Zhejiang,312000)

Using Gamma function and Cauchy’smean value theorem,two results of the exponential generalization on the Qi type integral inequality are established,the scope of the exponential establishment of Qi type integral inequality is still true from positive integer to any positive real number,from another angle,it answered an open problem proposed by professor F.Qi in 2000.In addition,a resultof Chen and Kimball in 2006 is revised to answer the open problem proposed by professor F.Qi.

Gamma function;Cauchy’smean value theorem;integral inequality;exponential generalization;open problem