拓扑绝缘体Sb2Te3和Bi2Te2Se薄膜电子结构的第一性原理研究

2015-06-07雷玉玺周剑平

陕西师范大学学报（自然科学版） 2015年4期

关键词：能隙第一性绝缘体

马静，雷玉玺，王园，周剑平

(陕西师范大学物理学与信息技术学院，陕西西安 710119)

拓扑绝缘体Sb2Te3和Bi2Te2Se薄膜电子结构的第一性原理研究

马静，雷玉玺，王园，周剑平*

(陕西师范大学物理学与信息技术学院，陕西西安 710119)

拓扑绝缘体；电子结构；金属表面态; 第一性原理

PACS: 73.50.-h

固体材料按照其导电性质可以分为导体和绝缘体，其中绝缘体材料在费米能级处存在着有限大小的能隙，因而没有自由载流子[1]。拓扑绝缘体是近几年发现的一种新的量子物质态，其绝缘机制不同于传统意义上的绝缘体[2-3]。这种物质态的体电子态是有能隙的绝缘体，而其表面则是无能隙的金属态。这种无能隙的表面金属态也完全不同于一般意义上的由于表面未饱和键或者是表面重构导致的表面态，拓扑绝缘体的表面金属态完全是由材料体电子态的拓扑结构所决定，即取决于其对称性，与表面的具体结构无关。也正是因为该表面金属态的出现是由对称性的变化所导致，因此它的存在非常稳定，基本不受非磁性杂质与无序的影响[4]。拓扑绝缘体表面能带结构存在“狄拉克锥”，即能带有上下锥形相连的结构，处于锥边缘态的电子自旋会呈现涡旋排列，形成所谓的自旋流并在磁场下表现出自旋霍尔效应[5]。

拓扑绝缘体是凝聚态物理最近几年的研究热点，涉及许多重要的物理现象和机制，并具有广阔的应用前景。其具有拓扑非平庸的绝缘性体电子结构和受时间反演对称性保护的金属性表面态，有可能在未来信息技术如容错量子计算、信息存储、热电器件、非线性光学、自旋电子学和拓扑量子计算等领域有重要应用[6-8]。

1 计算方法

在软件MedeA[12]环境下进行计算，选用密度泛函理论下的第一性原理程序包VASP[13],采用 Perdew Burke Ernzerhof(PBE)泛函下的广义梯度近似(Generalized Gradient Approximation，GGA)来描述电子与电子之间的交换关联能[14]，同时离子实与外层价电子之间的相互作用选用投影缀加平面波(PAW) 赝势[15]来描述。平面波截断能设为340 eV，薄膜的所有计算K点取样为7×3×1。参照以前研究中普遍采用的方案[16]，只优化原子内坐标，原子结构优化中的总能收敛判据(SCF)设置为10-5eV。只在电子结构计算中考虑了自旋轨道耦合作用(Spin-Orbit Coupling，SOC)[17]。为了消除上下表面在z轴方向的影响，将真空层厚度取为2 nm。

2.1 计算模型

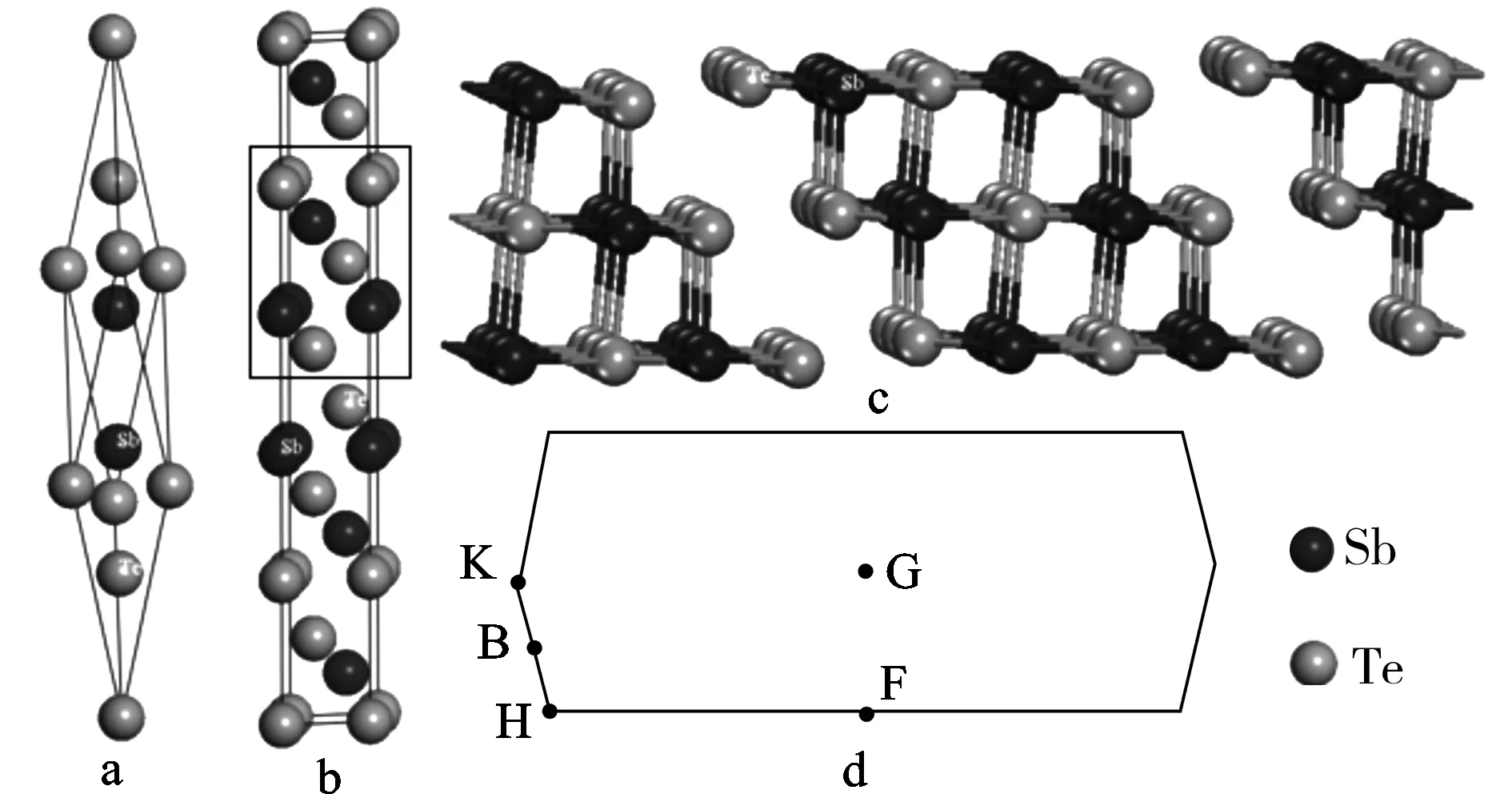
图1 Sb2Te3晶体的菱形原胞(a)，Sb2Te3的六角晶胞(b),层薄膜原子排列结构模型(c)和面二维布里渊区(d)Fig.1 The rhombohedral primitive cell of Sb2Te3 (a),hexagonal supercell of Sb2Te3 (b), atomic

2.2 计算结果与讨论

首先计算Sb2Te3的体块能带结构，如图2所示。

图2 Sb2Te3体材料的能带结构图Fig.2 Band structure of bulk Sb2Te3

从图2可以看出，体块Sb2Te3能带结构在考虑SOC情况下为间接带隙，其值为0.186eV，低于文献中的实验值0.232 eV[18]，导致计算偏差的主要原因是由于GGA近似对电子之间的交换关联作用处理不足。同时可以看到费米能级处Γ点附近的价带分裂成沿着Γ-F和Γ-L方向的2个小峰。

图3 不同层Sb2Te3薄膜能带结构

Fig.3 Band structures of Sb2Te3films with different layers

图4 不同层Sb2Te3薄膜态密度Fig.4 Density of states of Sb2Te3 films with different layers

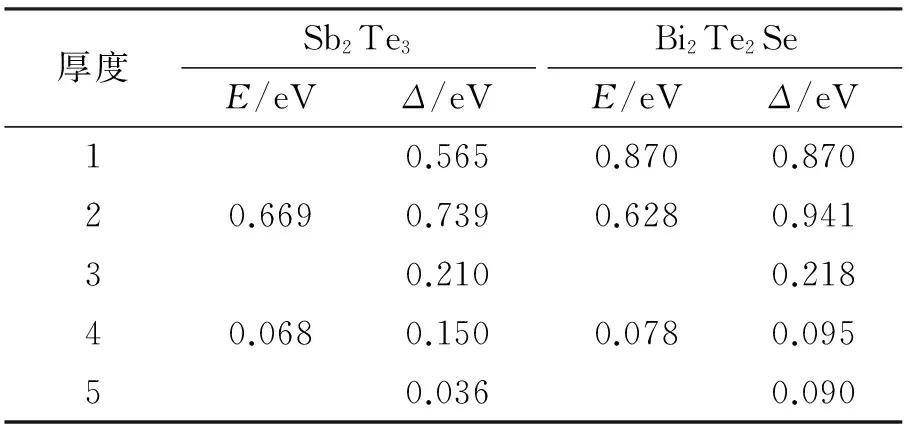
表1 不同膜厚下在G点处的能隙Δ和带隙ETab.1 The energy gap Δ at G and the band gap E

3.1 计算模型

图5 Bi2Te2Se晶体的菱形原胞(a),Bi2Te2Se的六角晶胞(b)和层薄膜原子排列结构模型(c)Fig.5 The rhombohedral primitive cell of Bi2Te2Se(a),hexagonal supercell of Bi2Te2Se(b) and the atomic

3.2 计算结果与讨论

图6为Bi2Te2Se体块在考虑SOC后的能带结构。其导带底位于Γ点，而价带顶在Z-F间，间接带隙为0.232 eV，低于文献中的实验值0.300 eV[19]，Γ点的能隙为0.451 eV。

图6 Bi2Te2Se体材料的能带结构图Fig.6 Band structure of bulk Bi2Te2Se

图7 不同层Bi2Te2Se薄膜能带结构Fig.7 Band structures of Bi2Te2Se films with different layers

4 结论

[1] 谢希德，陆栋. 固体能带理论[M].上海：复旦大学出版社，1998：153-228.

[2] Moore J. The birth of topological insulators[J].Nature, 2010, 464(7286): 194-198.

[3] Qi X L, Zhang S C. Topological insulators and superconductors[J].Reviews of Modern Physics, 2011,83(4):1057-1110.

[4] 吕衍凤，陈曦，薛其坤. 拓扑绝缘体简介[J].物理与工程, 2012,22(1):7-10.

[5] Bernevig B A, Hughes T L, Zhang S C. Quantum spin hall effect and topological phase transition in HgTe quantum wells[J].Science, 2006, 314(5806): 1757-1761.

[6] 翁红明，戴希，方忠. 磁性拓扑绝缘体与量子反常霍尔效应[J].物理学进展, 2014,34(1):1-9.

[7] 何珂，王亚愚，薛其坤. 拓扑绝缘体与量子反常霍尔效应[J].科学通报, 2014, 59(35):3431-3441.

[8] 叶飞，苏刚.拓扑绝缘体及其研究进展[J].物理, 2010, 39(8):564-569.

[9] Xu S Y, Wray L A, Xia Y, et al.Discovery of several large families of topological insulator classes with back scattering-suppressed spin-polarized single-Dirac-cone the surface[EB/OL].http://arxiv.org/abs/1007.5111.

[10] Park K, Heremans J J, Scarola V W, et al. Robustness of topologically protected surface states in layering of Bi2Te3thin films[J].Physical Review Letters, 2010, 105(18): 186801.

[11] Chang J, Register L F, Banerjee S K, et al. Density functional study of ternary topological insulator thin films [J].Physical Review B, 2011,83(23):235108.

[12] MedeA[CP].New Mexico: Materials Design, 2013.

[13] Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B, 1996, 54(16): 11169-11186.

[14] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J].Physical Review Letters, 1996, 77(18): 3865-3868.

[15] Blochl P E. Projector augmented-wave method[J].Physical Review B, 1994, 50(24): 17953-17979.

[16] Cho S, Kim Y, Ketterson J B. Structural and thermoelectric properties in (Sb1-xBix)2Te3thin films [J].Applied Physics A, 2004,79(7): 1729-1731.

[17] Luo X, Sullivan M B, Quek S Y. First-principles investigations of the atomic, electronic, and thermoelectric properties of equilibrium and strained Bi2Se3and Bi2Te3including van der Waals interactions[J].Physical Review B, 2012,86(18):184111.

[18] Zhang H, Liu C X, Qi X L, et al. Topological insulators in Bi2Se3, Bi2Te3and Sb2Te3with a single Dirac cone on the surface[J].Nature Physics, 2009, 5(6): 438-442.

[19] Ren Z, Taskin A A, Sasaki S, et al. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se[J].Physical Review B, 2010, 82(24): 241306.

〔责任编辑李博〕

First-principles studies of the electronic structures of topological insulator Sb2Te3and Bi2Te2Se films

MA Jing, LEI Yuxi, WANG Yuan, ZHOU Jianping*

(School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)