可压缩Navier-Stokes方程的球对称经典解
2015-06-07王梅,方莉
王 梅,方 莉
(西北大学 数学学院,陕西 西安 710127)
可压缩Navier-Stokes方程的球对称经典解
王 梅,方 莉
(西北大学 数学学院,陕西 西安 710127)
可压缩Navier-Stokes方程反映着流体力学研究的前沿,为了对其Vaigant-Kazhikhov模型的解进行深入研究,借鉴并推广了相关文献关于二维方程密度估计的方法到三维球对称情形,证明了外区域中Cauchy问题的球对称经典解的适定性。 证得当黏性系数λ(ρ)=ρβ时,β>14/5以及当初始密度远离真空状态时,解在有限时间段内也不会出现真空状态。
可压缩Navier-Stokes方程; 三维球对称; Cauchy问题; 全局适定性
三维球对称等熵可压Navier-Stokes方程
(1)
其中μ>0是常数,λ(ρ)=ρβ。给定初边值条件:
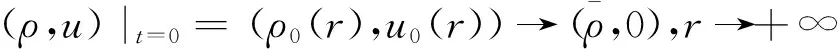
u(a,t)=0。
Navier-Stokes方程是刻画流体动力学的一个基本模型,其解的一般性质取决于其基本波的发展和相互作用,这些基本波包括激波、疏散波、扩散波、涡面、孤立子和边界层等。 有关可压Navier-Stokes方程的理论研究是近代数学物理研究的热门课题,吸引了许多学者从事这方面的研究[1-8],至今有许多问题仍未解决。
黏性系数依赖于密度的可压Navier-Stokes方程中的一维问题大部分已解决,这主要归功于拉格朗日坐标将方程形式的简化。然而,针对高维的Navier-Stokes方程,目前得到的结果却很少。当黏性系数依赖于密度时,要证明可压缩Navier-Stokes方程解的存在性,主要困难在于密度趋于真空时,流体的速度无法定义。其证明的关键是要估计密度的下界。Vaigant-Kazhikhov模型在文献[2]中被首次提出,该文证明了二维周期问题经典解的适定性;文献[3]建立了弱解的全局存在性以及解的大时间性态; 近年来,文献[4-6]研究了二维全空间中解的适定性问题。
不同于二维问题的计算,本文难点在于关于‖u‖∞的估计,本文充分利用球对称解的无旋性以及H1嵌入到L∞研究了当初值任意大并且在无穷远处非真空时外区域中解的适定性问题。
1 主要定理
定义势能函数
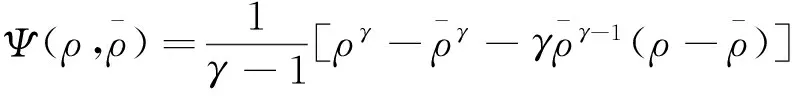
区域Ω={r∈R|r≥a,a>0}。
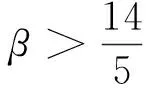
0 其中q、c、C是正常数满足q>2,0 C([0,T];W2,q(Ω)), H2(Ω))∩L2(0,T;H3(Ω))。 (2) 在下文中定义f∈Lp(Ω)⟺∫Ωfpr2dr<+∞。 定义有效黏性通量 涡度 2.1 基本能量估计 引理1假设(ρ0,u0)满足初值条件,则存在常数C依赖于(ρ0,u0),使得 2.2 密度估计 给动量方程(1)2作用div算子,则有 [div(ρu)]t+div[div(ρu⊗u)]=ΔF。 (3) 在区域Ω上,考虑下面3个椭圆方程: (4) (5) -Δη=div[div(ρu⊗u)]。 (6) 这3个方程都具有边界条件ξ1、ξ2、η→0(r→∞)。 特别地, (7) 引理3区域Ω上成立下列估计: (1) ‖u‖2m≤C(‖u‖2+1),∀m≥1; (4) ‖ξ2‖2m≤C,∀m≥3; 结合上面(3)—(6)以及边界条件则有 ξ1t+ξ2t+η+F=0。 由有效黏性通量F的定义 ξ1t+ξ2t+(2μ+λ(ρ))divu- 结合质量方程(1)1, 定义 因此,得到一个新的输运方程 (Λ(ρ)-ξ1-ξ2)t+u·(Λ(ρ)-ξ1-ξ2)+ (8) 引理4对任意的k≥2,β>1且r>a,有 (9) 证明给方程(8)乘以 ρ[Λ(ρ)-ξ1-ξ2)+]2m-1r2,其中m为任意大的正数,(…)+定义了(…)的正部。得到 (10) 定义 经过计算有, 将上面的不等式关于[0,t]积分, (11) (12) 经过计算, (13) 结合不等式(12),有 Cδ‖‖‖, 因此,引理4对任意的k≥2成立。 2.3 速度的一阶导数估计 引理5对任意的β≥1,有 (14) 因此,得到 2.4 上下界估计 引理7存在常数C1和c1,使得 c1≤ρ(t,x)≤C1,∀(t,x)∈[0,T]×Ω。 证明对任意p>2和q>1满足 有 CΦT(‖u‖。 (15) 通过方程(4)和(5)中ξi的定义,有 u·(ξ1+ξ2)-η=[u,RiRj](ρu), (16) 因此由方程(8)可以得到 [u,RiRj](ρu)=0, (17) 其中物质导数Dt∶=∂t+u·。定义质子轨道 因此,成立常微分方程 故 在[0,t]上积分上面的不等式,有 (18) C[‖u‖BMO‖ρu‖4]12≤ 并且由无旋性知, 因此, (19) 又因为 ‖ξ1+ξ2‖∞≤C(‖ξ1+ξ2‖2m+‖(ξ1+ (20) 将(19)和(20)式带入方程(18),有 (21) ρ(t,x)≥c1>0,∀(t,x)∈[0,T]×Ω。 在定理1的假设下, 经典解的局部存在性可以类似文献[7-8]的证明。对于可压缩Navier-Stokes方程这样一个椭圆-抛物耦合系统, 可用标准的延拓准则[4-5]通过第二部分中得到的密度上下界估计, 高阶的先验估计将局部解延拓到全局解, 从而得到定理1的证明。 [1] Jiu Q S,Wang Y,Xin Z P.Global classical solutions to the two-dimensional compressible Navier-Stokes equations in R2[EB/OL].http://arxiv.org/abs/1209.0157. [2] Vaigant V A, Kazhikhov A V.On the existence of global solutions of two-dimensional Navier-Stokes equations of a compressible viscous fluid[J].Siberian Mathematical Journal, 1995,36(6):1108-1141. [3] Perepelitsa M.On the global existence of weak solutions for the Navier-Stokes equations of a compressible fluid flows[J].SIAM Journal on Mathematical Analysis,2006,38(4):1126-1153. [4] Jiu Q S, Wang Y,Xin Z P.Global well-posedness of 2D compressible Navier-Stokes equations with large data and vacuum[EB/OL].http://arxiv.org/abs/1202.1382. [5] Jiu Q S, Wang Y, Xin Z P.Global well-posedness of the Cauchy problem of 2D compressible Navier-Stokes equations in weighted spaces[EB/OL].http://arxiv.org/abs/1207.5874. [6] Jiu Q S,Wang Y,Xin Z P.Global classical solutions to the two-dimensional compressible Navier-Stokes equations in R2[EB/OL].http://arxiv.org/abs/1209.0157. [7] Luo Z.Local existence of classical solutions to the two-dimensional viscous compressible flows with vacuum[J].Communications in Mathematical Sciences, 2012, 10(2): 527-554. [8] Solonnikov V A.On the solvability of the initial-boundary value problem for the equations motion of a viscous compressible fluid[J].Zapiski Nauchnykh Seminarov LOMI,1976,56:128-142. 〔责任编辑 宋轶文〕 The classical solutions to the spherically symmetric compressible Navier-Stokes equations WANG Mei, FANG Li (School of Mathematics, Northwest University, Xi′an 710127, Shaanxi, China) The compressible Navier-Stokes equations has an important position in the progress of fluid mechanics.In order to research the Vaigant-Kazhikhow model,the methods of related articles in 2D are referenced and the results of the 3D spherically symmetric situation are obtained.It is proved that the global well-posedness of the classical solution to the Cauchy problem of spherically symmetric compressible Navier-Stokes equations in an exterior domain.When the bulk viscosityλ(ρ)=ρβ,β>14/5,it is shown that the solution will not develop the vacuum states in any finite time provided the initial density is uniformly away from vacuum. compressible Navier-Stokes equations; 3D spherically symmetric; Cauchy problem; global well-posedness 35Q30 1672-4291(2015)04-0001-05 10.15983/j.cnki.jsnu.2015.04.141 2014-12-14 陕西省自然科学基础研究计划(2012JQ1020) 王梅,女,博士研究生,主要研究方向为流体力学中的偏微分方程理论。E-mail:wangmei0439@163.com O175 A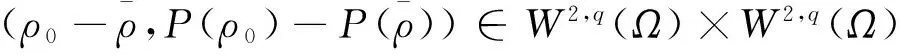
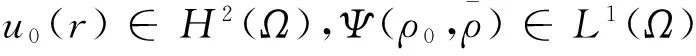

2 先验估计及主要结果的证明

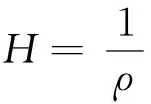
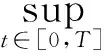



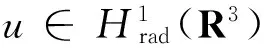
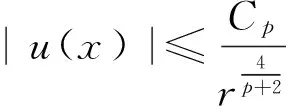

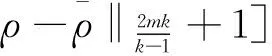



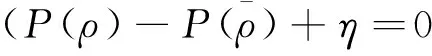

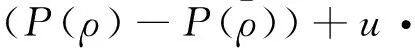


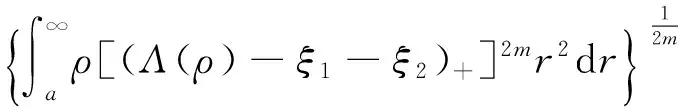




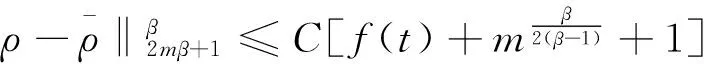






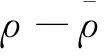
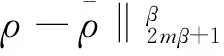
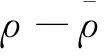
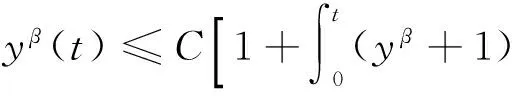
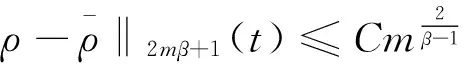



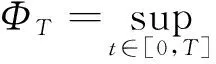

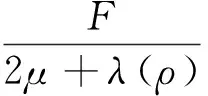

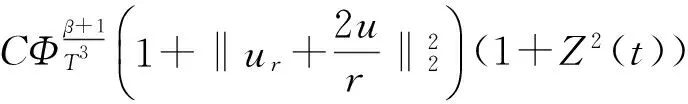
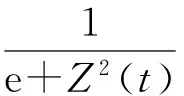
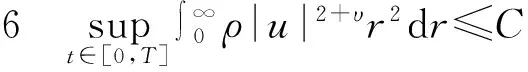



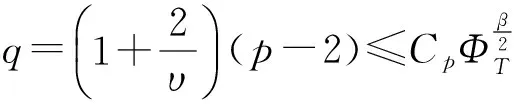


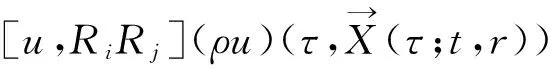
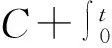




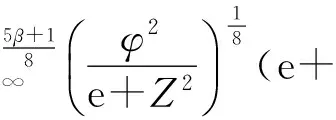
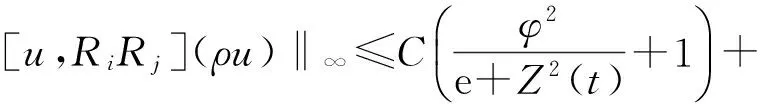


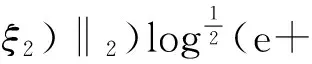


3 主要结果的证明
