MV-代数的(→,⊕)-微分
2015-06-07王军涛辛小龙贺鹏飞
王军涛,辛小龙,贺鹏飞
(西北大学 数学学院,陕西 西安 710127)
MV-代数的(→,⊕)-微分
王军涛,辛小龙*,贺鹏飞
(西北大学 数学学院,陕西 西安 710127)
在MV-代数上引入了(→,⊕)-微分,研究了MV-代数(→,⊕)-微分的性质。定义并研究了正则(→,⊕)-微分,并讨论了MV-代数的布尔中心上的(→,⊕)-微分的一些性质。给出了中心主微分的概念,用中心主微分讨论了(→,⊕)-微分与MV-代数其他微分之间的关系。并用中心主微分的不动点之集刻画了Boole代数。最后, 定义并研究了微分MV-代数的微分理想, 并讨论了正则微分MV-代数所有的微分理想组成的集合ID(A)的代数结构。
MV-代数;(→,⊕)-微分;微分理想;布尔代数;Heyting格
MV-代数在文献[1]提出后,不少学者对MV-代数的性质进行了研究,得到了一些重要的结论[2-3]。微分理论来源于分析学,将它引入到代数系统中有助于研究代数系统的结构和性质。一些学者在环和近似环上研究了微分算子的性质[4-5]。2004年文献[6]将环上的微分算子理论引用到BCI-代数中,得到了一些重要的结果。2008年文献[7]将微分算子的理论应用到格上,并利用保序微分算子刻画了模格、分配格。2013年文献[8]深入研究了MV-代数上的(⊙,⊕)-微分和(⊖,⊙)-微分,并刻画了保序(⊙,⊕)-微分。
本文在MV-代数上引入了(→,⊕)-微分的概念, 研究了MV-代数(→,⊕)-微分的一些性质。定义并研究了正则(→,⊕)-微分,并讨论了MV-代数的布尔中心上的(→,⊕)-微分的一些性质。进一步,给出了中心主微分的概念, 并用中心主微分的不动点之集刻画了Boole代数。最后,定义并研究了MV-代数的微分理想,得到了若d是A的幂等正则微分,则(ID(A),∧,∨,→,∅,A)是一个Heyting格,其中ID(A)是微分MV-代数的所有微分理想的集合。
1 预备知识
定义1[2]一个MV-代数是(2,1,0)型代数(A,⊕,*,0)满足下列公理:∀x、y、z∈A,
(MV1)x⊕(y⊕z)=(x⊕y)⊕z;
(MV2)x⊕y=y⊕x;
(MV3)x⊕0=x;
(MV4)x**=x;
(MV5)x⊕0*=0*;
(MV6) (x*⊕y)*⊕y=(y*⊕x)*⊕x。
在MV-代数A中记0*=1并定义二元运算⊙、∧、∨、→、⊖如下:
x⊙y=(x*⊕y*)*;x∨y=(x⊙y*)⊕y;x∧y=x⊙(x*⊕y);x→y=x*⊕y;x⊖y=x⊙y*。
显然,(A,⊙,1)是一个可换含幺半群,且(A,∧,∨,0,1)是有界分配格。在MV-代数中定义偏序关系“≤”为x≤y当且仅当x∧y=x,定义x*=x→0。若A中任意两元素都存在偏序关系,则称A是线性序的。另外,称B(A)={x∈A|x⊕x=x}={x∈A|x⊙x=x}为A的布尔中心,则(B(A),⊕,*,0)是一个布尔代数。
定理1[2]设A是MV-代数,则下列结论成立:∀x、y、z∈A,
(1)x⊕x*=1,x⊙x*=0;
(2) 若x≤y当且仅当x⊙y*=x⊖y=0当且仅当x→y=1;
(3) 若x≤y,则y→z≤x→z,z→x≤z→y;
(4)x⊙y≤x∧y≤x,y≤x∨y≤x⊕y;
(5)x∨y=(y→x)→x=(x→y)→y;
(6) 若x≤y当且仅当y*≤x*;
(7)x⊕y=y当且仅当x⊙y=x;
(8) (x⊖y)⊕y=x∨y,x⊖(x⊖y)=x∧y;
(9) (x⊖z)⊖y=(x⊖y)⊖z;
(10)x∧(y⊕z)=(x⊕z)∧(x⊕y)。
定理2[2]设A是MV-代数,则下列结论等价:
(1)x∈B(A);
(2)x⊕y=x∨y,∀y∈A;
(3)x⊙y=x∧y,∀y∈A。
定义2[1]设A是MV-代数,I是A的子集,若I满足以下条件:∀x、y∈A,
(1) 0∈I;
(2) 若x∈I,y∈A,且x≤y,则x∈I;
(3) 若x、y∈I,则x⊕y∈I。
则称I是A的理想。
定义3[9]设A是MV-代数,F是A上的子集,若F满足以下条件:∀x、y∈A,
(1) 1∈F;
(2) 若x∈F,y∈A且x≤y,则y∈F;
(3) 若x、y∈F,则x∧y∈F。
则称F是A的格滤子。另外,如果A的格滤子F满足:
(4)∀x、y∈F,若x∨y∈F,则x∈F,或y∈F。
则称F是A的格素滤子。∀α∈A,(a]表示由a生成的滤子,称(a]为主滤子,容易验证(a]={x∈A|x≥a}。
定义4[10]设P是偏序集,P上的二元运算⊕和⊖互为余伴随,若以下条件成立:
(1) ⊕:P×P→P是单调递增的;
(2) ⊖:P×P→P是关于第一变量不减,关于第二变量不增;
(3)c≤a⊕b当且仅当c⊖b≤a,a、b、c∈P。
定义5[11]设(L,∧,∨,→,0,1)为有界格,→为L上的二元运算。(L,∧,∨,→,0,1)是Heyting格,如果下列条件成立:x∧y≤z当且仅当x≤y→z,x、y、z∈L。
取健康小鼠,sc 0.2 mL苯甲酸雌二醇注射液(0.5 mg/mL),每2天1次,共3次。6 d后采用无菌PBS溶液灌洗小鼠阴道3次,将无菌石蜡油涂抹5号头皮针硅胶管,随后缓慢插入小鼠阴道约1.5 cm处,向阴道内接种大肠杆菌(1×109 cfu/mL)及金黄色葡萄球菌(1×109 cfu/mL)混合菌液,接种4 d后采集阴道分泌物涂片,进行革兰染色镜检,考察金黄色葡萄球菌及大肠杆菌感染情况,确定BV模型是否成功(当小鼠阴道明显充血、红肿并伴有大量脓性分泌物时,取分泌物涂片,镜下可见大量的感染菌和坏死细胞,表明小鼠BV模型制备成功[8-9])。
定义6[3]设A是一个MV-代数,d:A→A是映射。若d满足:∀x、y∈A,
d(x⊙y)=(d(x)⊙y)⊕(x⊙d(y)),
则称d是A的(⊙,⊕)-微分。
定义7[8]设A是一个MV-代数,d:A→A是映射。若d满足:∀x、y∈A,
d(x⊖y)=(d(x)⊖y)⊙(x⊖d(y)),
则称d是A的(⊖,⊙)-微分。
2 MV-代数上的(→,⊕)-微分
本文引入了MV-代数的(→,⊕)-微分,并研究它的一些重要性质。
定义8设A是一个MV-代数,d:A→A是映射。若d满足:∀x、y∈A,
则称d是A的(→,⊕)-微分,(A,d)为微分MV-代数。简记d(x)=dx。
例1设A是一个MV-代数,定义映射d:A→A为dx=1,∀x∈A,则容易验证d为(→,⊕)-微分,称d为平凡(→,⊕)-微分。
例2设A={0,a,b,1},其中0≤a≤b≤1。二元运算⊕和*如下:
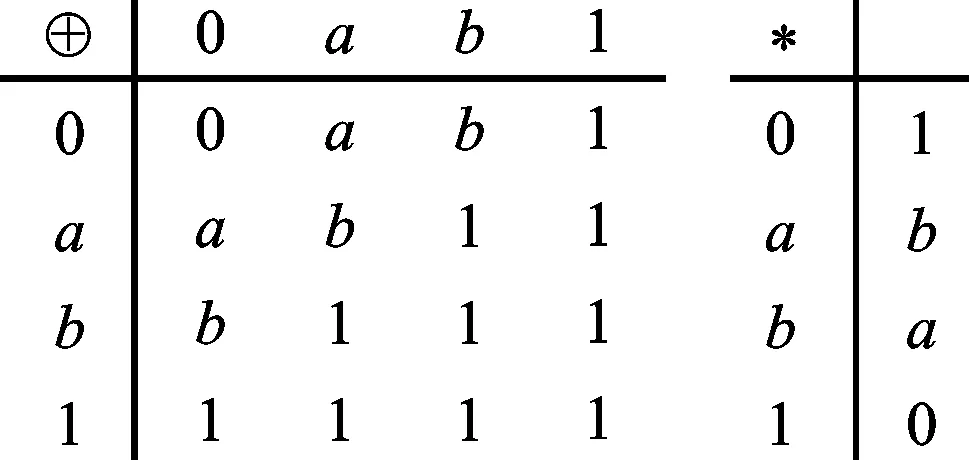
容易验证(A,⊕,*,0,1)是MV-代数。定义映射d:A→A如下:d0=b,da=db=d1=1,则d是A的(→,⊕)-微分。定义d1:A→A为d10=a,da=a,d1b=d11=b。由于d1(1→b)=d1b=b,(d11→b)⊕(1→d1b)=1≠b,因此d1不是A的(→,⊕)-微分。
注1例2中的(→,⊕)-微分d,由于d(a⊙b)=d0=b,(d(a)⊙b)⊕(a⊙d(b))=1≠b,因此d不是A的(⊙,⊕)-微分。又d(a⊖b)=b,(d(a)⊖b)⊙(a⊖d(b))=0≠b。故d不是A的(⊖,⊙)-微分。
命题1设d是MV-代数A的(→,⊕)-微分,则下列结论成立:∀x、y∈A,
(1)d1=1;
(2)dx=x⊕dx;
(3)x≤dx;
(4)x≤y,蕴含dx≤dy;
(5)dx→y≤x→dy;
(6)dx→dy≤d(x→y)。
证明(1)d1=d(1→1)= (d1→1)⊕(1→d1)=1。
(2)dx=d(1→x)=(d1→x)⊕(1→dx)=x⊕dx。
(3) 根据(2)知x≤x⊕dx=dx。
(4) 若x≤y,则y=x∨y,因此
dy=d(x∨y)=d((y→x)→x)=d((y→x)→x)⊕((y→x)→dx)≥ (y→x)→dx≥1→dx=dx。
(5) 由定理1(3)和(3)可得。
(6) 由定义8,定理1(3)和(3)可得。
定义9设d是MV-代数A的(→,⊕)-微分。若d0=0,则称d为MV-代数A的正则(→,⊕)-微分。
例3设A是例2中的MV-代数,定义映射d:A→A为d0=0,da=a,db=d1=1,容易验证d是A的正则(→,⊕)-微分。
命题2设d是MV-代数A的正则(→,⊕)-微分,则下列结论成立:∀x、y∈A,
(1) (dx)*≤dx*;
(2)d(x⊕y)≤dx⊕dy;
(3)dx⊖dy≤d(x⊖y)。
证明(1) 根据命题1(6)和d0=0可得。
(2) 由定义8,命题1(2)和(1)知d(x⊕y)=d(x*→y)=(d(x*)→y)⊕(x*→dy)≤(d(x)*→y)⊕(x*→dy)=dx⊕y⊕x⊕dy=(dx⊕x)⊕(dy⊕y)=dx⊕dy。因此,d(x⊕y)≤dx⊕dy。
(3) 由定理1(8),命题1(4)和(2)可知dx≤d((x⊖y)⊕y)≤d(x⊖y)⊕dy。从而
dx⊖dy≤d(x⊖y)。
下面讨论MV-代数A布尔中心上的(→,⊕)-微分的一些性质,并给出了MV-代数A布尔中心上的(→,⊕)-微分的等价刻画。
命题3设d是MV-代数A的(→,⊕)-微分。则以下结论成立:∀x、y∈B(A),
(1)d(B(A))⊆B(A);
(2)d(x→y)=(d(x)→y)∨(x→d(y);
(3)d(x→y)=dx→dy;
(4)d(x∨y)=dx∨dy;
(5) 若d0=0,dx*=(dx)*;
(6) 若d0=0,d(x∧y)=dx∧dy。
证明(1) 设x∈B(A)。由命题1(2)和定理2可知d(x)=d(x⊙x)=(x⊙x)⊕dx=dx∨(x⊙x)=(dx∨x)⊙(dx∨x)=(dx⊕x)⊙(dx⊕x)。因此,
dx=dx⊙dx。
(2) 设x、y∈B(A)。由(1)和定理2(2)可知
d(x→y)=(d(x)→y)⊕(x→d(y))= (d(x)→y)∨(x→d(y))。
(3) 由(2)和命题1(6)可得
d(x→y)=dx→dy。
(4) 由(3)和定理1(5)可知d(x∨y)=d((y→x)→x)=d(y→x)→dx=(dy→dx)→dx=dx∨dy,从而d(x∨y)=dx∨dy。
(5) 由(3)和d0=0可知
d(x→0)=dx→d0=(dx)*。
(6) 由(4)和(5)可得d(x∧y)=dx∧dy。
推论1设d是MV-代数A上的一个映射。则以下结论等价。
(1)d是B(A)上的(→,⊕)-微分;
(2)d(x→y)=x→dy,∀x、y∈B(A)。
证明(1)⟹(2)由命题1(5)和3(2)可得。
(2)⟹(1)假设d是B(A)上的映射且满足∀x、y∈B(A),d(x→y)=x→dy。则d1=d(1→d1)=d1→d1=1。又1=d1=d(x→x)=x→dx,因此∀x∈B(A),x≤dx。由定理1(3)可知dx→y≤x→dy。因此
d(x→y)=x→dy=(dx→y)⊕(x→dy)。
设A是MV-代数。d:A→A是一个映射。定义Fd(A)={x∈A|dx=x}。
命题4设d是MV-代数A的(→,⊕)-微分。则Fd(A)⊆B(A)。
证明设x∈Fd(A)。由命题1(2)可知dx=x⊕dx,所以x⊕x=x,因此x∈B(A)。
注2命题4的逆命题一般不成立。
例4设A是例2中的MV-代数,定义A上的映射d为d0=da=d1=0,db=1。则容易验证Fd(A)={0}⊆{0,1}=B(A),但是d不是A上的(→,⊕)-微分,因为
d(1→a)=da=0≠a=(d1→a)⊕(1→da)。
定理3设A是MV-代数,则以下结论等价。
(1)A是Boole代数;
(2) 恒等映射是(→,⊕)-微分。
证明(1)⟹(2)假设A是Boole代数且d是A上的恒等映射,则d(x→y)=x→dy。由推论1可知,d是Boole代数A的(→,⊕)-微分。
(2)⟹(1)假设恒等映射d是A上的(→,⊕)-微分。由命题4可知A=Fd(A)⊆B(A),因此A是Boole代数。
由定理3可知,若A是Boole代数,则恒等映射是A的(→,⊕)-微分。下面这个定理给出了Boole代数上的恒等(→,⊕)-微分的等价刻画。
定理4设d是Boole代数A上的(→,⊕)-微分,则以下结论等价。
(1)d是恒等映射;
(2)x→dy=dx→y;
(3)d是单射。
证明(1)⟹(2)显然。
(1)⟹(3)显然。
(2)⟹(1)假设∀x、y∈A,x→dy=dx→y。由推论1可知dx=d(1→x)=1→dx=d1→x=1→x=x。因此d是恒等映射。
(3)⟹(1)假设d是单射。∀x∈A,d(dx→x)=dx→dx=1=d1,因此dx→x=1,即dx≤x。根据命题1(3)得dx=x,∀x∈A。
命题5设A是MV-代数,a∈A,定义da:A→A为∀x∈A,da(x)=a⊕x,若da(A)⊆B(A),则da是A的(→,⊕)-微分。
证明由定义1、定理2知∀x、y∈A,(dax→y)⊕(x→da(y))=((da(x))*⊕y)⊕(x*⊕day)=((da(x))*⊕x*)⊕(day⊕y)=(da(x))*∨x*)⊕(day∨y)=x*⊕day=a⊕(x→y)=da(x→y)。由定义8知,da是A的(→,⊕)-微分。
注3由于da是MV-代数A的布尔中心上的(→,⊕)-微分。称da为MV-代数A的中心主微分。
命题6设A是MV-代数。则存在A上的自映射ga(y)=y⊖a使得(da,ga)是A上的一对余伴随。
证明显然⊕是单调不减的,⊖关于第一变量不增,关于第二变量不减并且∀x、y、a∈A,若y≤x⊕a⟺x≥y⊖a。由定义4可知(da,ga)是A上的一对余伴随对。
命题7设A是MV-代数。则ga是(⊖,⊙)-微分当且仅当ga⊆B(A)。
证明设ga(A)⊆B(A)。设x、y∈A,由定理1(9)和2知(gax⊖y)⊙(x⊖ga(y))=((ga(x))⊙y*)⊙(x⊙(gay)*)=((ga(x))⊙x)⊙((gay)*⊙y*)=(ga(x)∧x)⊙((gay)*∧y*)=gax⊙(y)*=ga(x)⊖y=(x⊖a)⊖y=(x⊖y)⊖a=ga(x⊖y)。由定义7可知ga是MV-代数的(⊖,⊙)-微分。
反之,若ga是A的(⊖,⊙)-微分。则x⊖a=ga(x)=ga(x⊖0)=(ga(x)⊖0)⊙(x⊖ga(0))=(x⊖a)⊙(x⊖a)。即ga(A)⊆B(A)。
命题8设A是MV-代数。则ga是(⊙,⊕)-微分如果ga(A)⊆B(A)。
证明设ga(A)⊆B(A)。设x、y∈A,ga(x⊙y)=((x⊙y)⊖a)⊕((x⊙y)⊖a)=((x⊖a)⊙y)⊕((x⊖a)⊙y)=(gax⊙y)⊕(x⊙gay)。由定义6可知ga是(⊙,⊕)-微分。
引理1[8]设d是MV-代数A的(⊙,⊕)-微分,则下列结论等价:
(1)d是保序的;(2)dx=x⊙d1。
命题9(1) 设A是MV-代数,d是A上的保序(⊙,⊕)-微分。若存在A上的自映射f满足fA⊆B(A),且(d,f)是A上的一对余伴随对,则f是A上的(→,⊕)-微分。
证明由命题5、6、8可证。
(2) 设A是Boole代数,g分别是A上的(⊖,⊙)-微分,若存在A上的自映射f满足(g,f)是A上的余伴随对。则f是A上的(→,⊕)-微分。
证明由命题5、6、7可证。
定理5设d是MV-代数A上的正则(→,⊕)-微分,则以下结论等价。
(1)A是Boole代数;
(2)Fd(A)是A的格滤子。
证明(1)⟹(2)假设A是Boole代数且d是A上的正则(→,⊕)-微分。由命题3(6)可得d(x∧y)=dx∧dy。若x、y∈Fd(A),则dx=x,dy=y,从而d(x∧y)=dx∧dy=x∧y,则x∧y∈Fd(A)。下面证明Fd(A)是A的上集。若x∈Fd(A),y∈A且x≤y,则dy=d(x∨y)=d((y→x)→x)=(d(y→x)→x)⊕((y→x)→dx)≤((y→x)→x)⊕((y→x)→x)=y⊕y=y,从而dy≤y。另一方面,由命题1(3)知y≤dy,故y=dy因此Fd(A)是A的格滤子。
(2)⟹(1)假设fd(A)是A的格滤子。由正则(→,⊕)-微分的定义可知0∈Fd(A)。从而Fd(A)=A。由命题4知A⊆B(A),故A是Boole代数。
定理6设d是A上的(→,⊕)-微分,则以下结论等价:
(1)A是Boole代数;
(2) 每一个主中心微分da满足Fda(A)=(a]。
证明(1)⟹(2)设A是Boole代数,则∀x∈A,x⊕x=x成立。由于da(a)=a⊕a=a,则a∈Fda(A)。根据定理5得Fda是A的上集,因此对任意a≤x,有x∈Fda(A),从而(a]⊆fda(A)。另一方面,设x∈Fda(A),则da(x)=x=a⊕x≥a∨x≥a。从而x=a∨x,即a≤x。这就证明了x∈(a]。因此,Fda(A)=(a]。
(2)⟹(1) 由(2)知∀a∈A,Fda(A)=(a],由于a∈(a],则a∈Fda(A),从而有a⊕a=da(a)=a,∀a∈A成立,即A是一个Boole代数。
3 微分MV-代数的微分理想
这一节,定义并研究微分MV-代数的微分理想,并讨论MV-代数的正则微分同余和正则微分理想之间的关系。最后,讨论了微分MV-代数所有的微分理想组成的集合ID(A)的代数结构。
性质1[1]设A是MV-代数,∅≠X⊆A⊕记〈X〉={a∈A|a≤x1⊕x2…xn,xi∈X,i=1,…,n}。则〈X〉是包含X的最小理想,称之为由X生成的理想。
若I是A的理想且x∈A,则〈I∪{x}〉={a∈A|c⊕xn≥a,∃c∈I,n∈N}。
定理7[1]若I是MV-代数的理想。定义xRy当且仅当x⊖y⊕y⊖x∈I。则R是MV-代数A上的同余关系。
所有的同余等价类记为A/I,即A/I={[x]|x∈A},其中[x]={y∈A|xRy}。定义+和*如下:
[x]+[y]=[x⊕y],[x]*=[x*]。
则(A/I,+,*,[0],[1])是一个MV-代数。
定义10设d是MV-代数A上的(→,⊕)-微分。I是MV-代数的理想,则I称为微分MV-代数的微分理想若dI⊆I。
记微分MV-代数的所有微分理想组成的集合为ID(A)。
例5设A={0,a,b,1}。二元运算⊕和*如下:

容易验证(A,⊕,*,0,1)是MV-代数。定义映射d:A→A如下:d0=da=a,db=d1=1,则d是A的(→,⊕)-微分。显然{0,a}是微分MV-代数的微分理想。虽然{0,b}是MV-代数的理想,但不是微分MV-代数的微分理想,因为db=1∉{0,b}。
命题10设d是MV-代数A的正则(→,⊕)-微分,x∈Fd(A),I是MV-代数的理想。则〈x∪I〉是微分MV-代数的微分理想。
证明若z∈〈a∪I〉,则存在y∈I使得z≤x⊖y。由命题1(4)和命题2(2)知dz≤d(x⊕y)≤dx⊕dy=x⊕dy,又dy∈I,因此dz⊖〈x∪I〉。
定理8设d是MV-代数A的幂等正则(→,⊕)-微分,I是MV-代数的理想,则I是微分MV-代数的正则微分理想当且仅当I=(I∩Fd(A)]。
证明一方面,假设d是MV-代数A的幂等正则(→,⊕)-微分且I是A的微分理想。x∈I,则dx∈I。从而dx∈I∩Fd(A)。由命题1(3)知x≤dx,所以x∈(I∩Fd(A)]。
反之,若x∈(I∩Fd(A)]。则存在y∈I∩Fd(A),使得x≤y。由命题3.2(4)知dx≤dy=y,所以x∈I。
定义11设d是MV-代数A的(→,⊕)-微分。A上的同余关系R被称为微分同余若∀x、y∈A,xRy当且仅当dxRdy。
记微分MV-代数的所有微分同余组成的集合为CD(A)。
定理9设d是MV-代数A的幂等正则(→,⊕)-微分,则ID(A)和CD(A)之间存在一个一一对应。
考虑下面的映射:
g:ID(A)→CD(A),I→ΘI
h:CD(A)→ID(A),Θ→[0]Θ
设d是MV-代数A上的幂等正则(→,⊕)-微分。∀x、y∈A,(x,y)∈Θ⟺(x⊖y)⊕(y⊖x)∈I,因为I是MV-代数一个微分理想,因此d(x⊖y),d(y⊖x)∈I。由命题2(3)知dx⊖dy,dy⊖dx∈I,因此(dx,dy)∈Θ。从而,ΘI是微分MV-代数的一个正则微分理想。
反之,若ΘI是微分MV-代数的一个正则微分同余。显然[0]Θ是微分MV-代数的一个微分理想。
显然gh(ΘI)=ΘI且hg(I)=I,对任意的ΘI∈CD(A)和I∈ID(A)。
定理10设d是MV-代数A的幂等正则(→,⊕)-微分,则(ID(A),∧,∨,→,∅,A)是一个Heyting格。
在ID(A)定义二元关系≤为J≤K当且仅当J⊆K,并规定∀J、K∈ID(A),J∧K=J∩K,J∨K={z∈A|z≤j⊕k,dz∈J∩K,j∈J,k∈K},J→K={z∈A|∀j∈J,j∧dz∈K}。
证明容易验证≤是ID(A)的偏序关系,J∧K是J、K的下确界。∅、A分别是(ID(A),≤)的最小元和最大元。
首先证J∨K是微分MV-代数的微分理想。显然0∈J∨K。假设y∈J∨K且x≤y,下证x∈J∨K。由y∈J∨K可知存在j1∈J,k1∈K,使得y≤j1⊕k1且dy∈J∩K。由J∧K是微分理想且dx≤dy可知dx∈J∩K。从而x∈J∨K。
设x、y∈J∨K,则存在j1、j2∈J,k1、k2∈K使得a≤j1⊕k1,b≤j2⊕k2且da、db∈J∩K。从而a⊕b≤(j1⊕j2)⊕(k1⊕k2),因为J和K是MV-代数的微分理想,因此j1⊕j2∈J,k1⊕k2∈K。由命题2(2)和J∩K是微分理想知d(a⊕b)≤d(a)⊕d(b)∈J∩K。因此a⊕b∈J∨K。若x∈J∨K,则存在dj∈J,dk∈K使得dx≤d(j⊕k)≤dj⊕dk且d(d(x))=d(x)∈J∩K。因此J∨K是微分理想。
再证J∨K=〈J∪K〉,即J∨K是J和K的上确界。
显然J≤J∨K,K≤J∨K,从而J∪K≤J∨K。因此〈J∪K〉≤J∨K。
反之,设x∈J∨K,则存在j∈J,k∈K使得x≤j⊕k,dx∈J∩K⊆J∪K⊆〈J∪K〉。由命题1(2)可知x∈〈J∪K〉。因此J∨K≤〈J∪K〉。故J∨K=〈J∪K〉。
所以(ID(A),∧,∨,∅,A)是一个有界格。
再证J→K是微分理想。显然0∈J→K。假设y∈J→K且x≤y,则存在j∈J,j∧dy∈K。由命题1(4)可知j∧d(x)∈K。所以x∈K。假设x、y∈J→K,则j∈J,j∧d(x),j∧d(y)∈K。因此,(j∧d(x))⊕(j∧d(y))∈K。由定理1(10)知j∧d(x⊕y)∈K。因此x⊕y∈J→K。显然x∈J→K,d(x)∈J→K。因此J→K是微分理想。
最后证(ID(A),∧,∨,→,∅,A)是一个Heyting格。只需证J∧K≤L当且仅当J≤K→L。
设J∧K≤L。设x∈J则dx∈J。从而∀k∈K,k∧d(x)≤d(x),k∧d(x)≤k。因此k∧d(x)∈J∧K≤L。故x∈K→L。所以J≤K→L。
反之,设J≤K→L。设x∈J∧K,则x∈K→L。∀k∈K,k∧d(x)∈L。令k=x∈K,有k∧dx=x∈L。因此J∧K≤L。
由定义5可知(ID(A),∧,∨,→,∅,A)是一个Heyting格。
定理11设(A,d)是一个微分MV-代数,I是微分MV-代数的任意一个微分理想,则(A/I,g)是一个微分MV-代数。
证明设d是MV-代数A的一个(→,⊕)-微分。定义一个映射g:A/I→A/I为g(xI)=d(x)I∀x∈A/I。若a、b∈A满足aI=bI,则a∈bI。因为I是微分MV-代数的一个微分理想,因此dI⊆I。从而有da∈d(bI)⊆(db)I。所以g(aI)=g(bI)。从而映射g是良定的。
设xI、yI∈A/I,g(xI→yI)=(d(x→y)I。因为d是MV-代数A上的(→,⊕)-微分。所以(d(x→y)I=((dx→y)⊕(x→dy))I=(g(xI)→yI)⊕(xI→g(yI))。由定义8可知g是微分MV-代数上的一个(→,⊕)-微分。
5 结束语
在MV-代数上引入了(→,⊕)-微分,研究了MV-代数(→,⊕)-微分的一些性质。定义并研究了正则(→,⊕)-微分,并讨论了MV-代数的布尔中心上的(→,⊕)-微分的一些性质。进一步,给出了中心主微分的概念,用中心主微分讨论了(→,⊕)-微分与MV-代数其他微分之间的关系。并用中心主微分的不动点之集刻画了Boole代数。最后,定义并研究了微分MV-代数的微分理想,得到了若d是A的幂等正则微分,则微分MV-代数所有的微分理想构成了一个Heyting格。
[1] Chang C C. Algebraic analysis of many valued logics[J].Transactions of American Mathematical Society, 1958, 88(2): 467-490.
[2] Cignoli R, Dottaviano I D, Mundici D. Algebra foundations of many-valud reasoning[M].Dordrechet: Kluwer Academic Publishers,2000.
[3] Alshehri N O. Derivations of MV-algebras[J].Internation Journal of Mathematics and Mathematical Sciences, 2010: 312027.
[4] Posner E. Derivations in prime rings[J].Proceedings of the American Mathematical Society, 1957, 8(6):1093-1100.
[5] Bell H E, Mason G. On derivations in near-rings and near-fields[J].North-Holland Mathematics Studies, 1987, 137:31-35.
[6] Jun Y B, Xin X L. On derivation of BCI-algebras[J].Information Sciences, 2004, 159(3):167-176.
[7] Xin X L, Li T Y,Lu J H. On derivations of lattice[J].Information Sciences, 2008, 178:307-316.
[8] Ghorbani S H, Torkzadeh L, Motamed S. (⊙,⊕)-derivations and (⊙,⊕)-derivations on MV-algebras[J].Iranian Journal of Mathematical Sciences and Informatics, 2013, 8: 75-90.
[9] Birkhoof G. Lattice theory[M].New York: American Mathematical Society Colloquium, 1940.
[10] 王国俊. 非经典数理逻辑与近似推理[M].北京:科学出版社, 2000.
[11] 郑崇友, 樊磊, 崔宏斌.Frame与连续格[M].2版.北京:首都师范大学出版社, 2000.
〔责任编辑 宋轶文〕
On (→,⊕)-derivations of MV-algebras
WANG Juntao, XIN Xiaolong*, HE Pengfei
(School of Mathematics, Northwest University,Xi′an 710127, Shaanxi, China)
The notion of (→,⊕)-derivations on MV-algebras is introduced and some properties of them are discussed.The regular (→,⊕)-derivations and the relationship between (→,⊕)-derivations and others derivations for MV-algebra are determined.Moreover,boolean algebras by the fixed set of principal center (→,⊕)-derivations are characterized.In addition,differential ideal of differential MV-algebras are studied.In particular,algebraic structures of the set ID(A) of all differential ideals on regular differential MV-algebras are researched.
MV-algebra; (→,⊕)-derivation; Boolean algebra; fixed point; differential ideal; Heyting lattice.
06D35
1672-4291(2015)04-0016-06
10.15983/j.cnki.jsnu.2015.04.144
2014-11-10
国家自然科学基金(11461025)
王军涛,男,硕士研究生,研究方向为逻辑代数与超代数。E-mail:1105020678@qq.com
*通信作者:辛小龙,男,教授,博士生导师。E-mail:xlxin@nwu.edu.cn
O153
A
