FDTD法计算刚性球形粒子离轴声辐射力
2015-06-07孙秀娜张小凤张光斌常国栋
孙秀娜, 张小凤, 张光斌,汪 艳, 常国栋
(陕西师范大学 物理学与信息技术学院,陕西省超声学重点实验室,陕西 西安 710119)
FDTD法计算刚性球形粒子离轴声辐射力
孙秀娜, 张小凤, 张光斌*,汪 艳, 常国栋
(陕西师范大学 物理学与信息技术学院,陕西省超声学重点实验室,陕西 西安 710119)
为了更精确、简便计算物体的声辐射力,应用时域有限差分算法对声波波动方程在时间和空间上进行差分离散化,通过设置有效的边界条件,完成声压场和速度场在时域上的迭代。将时域有限差分法与应力张量方程相结合,求出了二维情况下水中刚性球形粒子的声辐射力,研究了声辐射力随频率和粒子偏离高斯波束中心距离的变化关系。仿真结果表明,刚性球形粒子在高斯声场中的声辐射力随着粒子轴向偏离波束中心距离的增大而减小。当刚性球形粒子偏离波束轴时,轴向声辐射力与轴向、横向的偏移距离成反比。横向声辐射力随横向偏移距离的增加先增大后减小,在偏移波束中心两侧的距离相同时,辐射力的大小相等,方向相反。
时域有限差分法;高斯波束;离轴声辐射力;数值仿真
PACS: 43.35.+d
声辐射力因其无损、非接触等特性被广泛地应用到声悬浮、声学粒子操控、超声给药等各个领域。近年来,随着微操控技术的快速发展,利用声辐射力操控微纳米颗粒成为物理、生物、工程等领域的热门研究方向。
声辐射力的研究,开始于上世纪30年代。1934年,King首次计算了驻波和行波声场中刚性小球的声辐射力,给出了理想流体中刚性球声辐射力的解析表达式,该研究奠定了声操控技术理论基础。随后,各国学者就声辐射力的理论进行了不懈的研究。目前,有关声辐射力的理论研究,主要包括米氏散射法、声线法和时域有限差分法。米氏散射法是利用解析理论,通过求解波动方程计算声场,进而求解声辐射力,但是这种方法只能对球形粒子或者无限长的圆柱等规则形状物体进行求解。文献[1-3]利用米氏散射法研究了规则声场下粒子的声辐射力特性。声线法是声波的波长相对散射体尺寸非常小,衍射被忽略时,将声波看成类似光线的声线,用声线的疏密来表示声场的强弱,进而来计算声辐射力的方法,只适用物体尺寸远大于波长的情况。文献[4-5]采用声线理论计算了声场中任意位置流体小球的声辐射力,给出了声辐射力与粒子捕获能力的关系。
时域有限差分法(Finite Difference Time Domain Method ,FDTD)被广泛地应用于电磁波传播和散射的数值仿真中[6]。它通过直接离散Maxwell方程计算电磁场,不需要任何形式的导出方程,故不会因为数学模型而限制其应用范围,其差分方程中直接包含介质的参量,只须赋予各网格相应的参量,就能模拟各种散射体的结构。目前,基于时域有限差分法与麦克斯韦应力张量方程相结合的方法计算光俘获力的准确性已经得到了多次验证。 2010年,蔡飞燕、程欣等首次运用时域有限差分法计算了声场中的辐射力[7-8]。本文应用时域有限差分法,结合应力张量方程,计算了高斯波束作用下水中刚性球形粒子在声场中的不同位置时的声辐射力与轴向、横向偏移距离的变化关系。计算结果与利用米氏散射法计算得出的声辐射力非常一致;并且时域有限差分法不需要借用数学工具来推导大量公式,对物体的尺寸、形状、物理性质没有特殊的限定。
1 基于FDTD的声辐射力计算
1.1 声波动方程的离散化
在均匀的流体介质中,二维直角坐标下的声波方程为

(1)

(2)

(3)
式中:c为介质声速,ρ为介质密度,vx、vy为质点在x和y方向的振动速度,p为质点声压。
用FDTD仿真声场时,首先将(1)—(3)式的微分方程转化为离散差分方程,在时间轴上逐步推进求解。 由于计算区域是有限的,声波在计算区域的边界处会发生反射,影响声波的正常传播。为了减小在边界处反射波的影响,选择完全匹配层吸收边界条件(Perfectly Matched Layer,PML)[9]。为使声波在PML中快速衰减,需要对声波波动方程进行指数差分变换。为了便于计算,将(1)—(3)式中的声压p分解为两个子分量px和py,引入衰减系数αx和αy,使声压和速度在PML层中以指数衰减。完全匹配层吸收边界条件内部的指数差分公式为

(4)

(5)

(6)
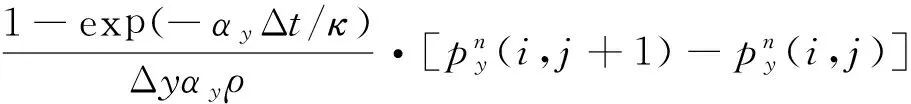
(7)

1.2 应用FDTD计算声辐射力
声辐射力的求解是对物体表面的应力张量进行迭代积分,即

(8)
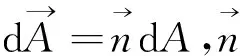

(9)
在时域有限差分算法中,声压和速度分量在时间和空间上是交错分布的。求解声辐射力时,需要计算的是物体表面上分布的网格点处的应力张量。由于声场是不断变化的,计算声辐射力时,对瞬时辐射力取一个周期进行时间平均,即

(10)
式中T为入射激励源的周期。
为了方便计算,利用傅里叶变换将声压从时域变换到频域,即

(11)
式中ω为入射波的角频率,N为时间迭代次数。当对所有变量做傅里叶变换后,每个Yee网格的法向和切向力的表达式[12]可以分别表示为

(12)
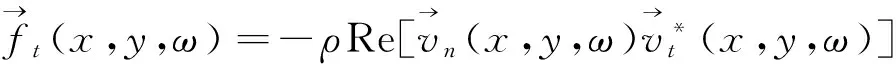
(13)




(14)
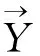
I=∫〈p2〉/(ρc2)dl。
(15)
其中l是绕物体表面的长度。
2 数值仿真
2.1 边界仿真
为了验证加入PML吸收边界条件的时域有限差分法的计算区域满足无限大区域声场的仿真要求,在Matlab软件中对一个连续上升余弦激励源在水中的声场进行了仿真。仿真时的参数设置为:二维计算区域400×400网格,网格间隔Δx=Δy=λmin/20,其中λmin=c/fmax是最小波长,最大频率fmax=3 750 Hz,时间步长Δt=Δx/2c,声速c=1 500 m/s,完全匹配层个数h=10,衰减因子m=1.8。图1和图2分别为未加边界和加入PML吸收边界时1 000时间步的声场仿真结果。由图1和图2的比较可以看出,未加边界时,声波传到边界被反射回来,入射波和反射波在计算区域相互叠加。加PML吸收边界后,声波被匹配层吸收,几乎看不到反射波,有效解决了用有限区域模拟无限大区域声场的问题。

图1 未加边界条件的声波传播Fig.1 Acoustic wave propagation without boundary conditions

图2 加PML边界条件的声波传播Fig.2 Acoustic wave propagation with PML boundary condition
2.2 调制高斯脉冲波源的仿真
设声源为调制高斯脉冲波源,其声压表达式为
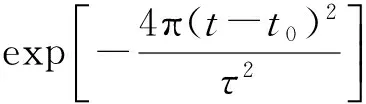
(17)
其中:x0是高斯波波束中心的坐标,w是高斯波束的束腰半径。ω是调制高斯脉冲波的角频率,τ是脉冲宽度。仿真时的参数设置为:x0=200网格处,角频率ω=24 000,脉冲宽度τ=9π/(2w),其他参数设置同2.1节。利用FDTD方法,分别对束腰半径为w=0.01λ和w=λ时,200时间步的高斯声场进行了仿真,结果如图3和图4所示。

图3 高斯波束束腰半径w=0.01λ时声场的分布Fig.3 The acoustic distribution field of Gaussianbeam with beam width w=0.01λ

图4 高斯波束束腰半径w=λ时声场的分布Fig.4 The acoustic distribution field of Gaussian beam with beam width w=λ
从图3和图4的仿真结果可以看出,高斯波束的束腰半径不同,对应的声场空间分布不同。束腰半径相对于波长较小时,高斯波的传播规律接近于点源的传播。当束腰半径等于1倍波长时,高斯波束相当于一条线形波源,声波强度在空间上呈现高斯分布。
2.3 声辐射力的数值仿真
2.3.1 声辐射力随频率的变化 对水中刚性球形粒子在高斯波束作用下的离轴声辐射力进行了仿真。仿真时的参数设置为:计算区域1 000×1 000网格,声速c=1 500 m/s,水的密度ρ=1×103kg/m3,刚性球形粒子的半径a=40Δx。调制高斯脉冲波的束腰半径取1倍波长。高斯波束的中心位置位于x0=500,y0=30网格处,球形粒子位于x=500,y=110网格处。根据(14)式,分别计算出刚性球形粒子的轴向和横向声辐射力随无量纲频率ka的变化关系曲线,如图5、图6所示。

图5 轴向声辐射力随ka的变化关系Fig.5 The relationship of axial acoustic radiation force and ka

图6 横向声辐射力随ka的变化关系Fig.6 The relationship of transverse radiation force and ka
从图5的仿真结果可知,在ka接近于0的位置处,轴向声辐射力是一个负值,随ka的增大逐渐由负值趋向于0逐渐变化为正辐射力,并随ka的增大而迅速增大,达到一个最大值。在ka<1时,轴向声辐射力随ka的增加有一个剧烈的波动,从负方向上的最大值变化到正方向上的最大值。不仅力的大小迅速变化,力的方向也发生改变。在1
2.3.2 声辐射力与粒子沿轴向偏离波束中心距离的关系 利用FDTD方法,对高斯声场中刚性球形粒子的声辐射力随粒子沿轴向偏移波束中心的距离的变化关系进行了研究。数值仿真中,取高斯脉冲波的束腰半径w=λ。刚性球形粒子沿着传输轴从90网格移动到610网格处。刚性球形粒子所受到的声辐射力与偏移距离的关系如图7所示。

图7 轴向声辐射力随y/a的变化关系Fig.7 The relationship of axial radiation force and y/a
图7中横坐标是粒子距离波束中心的轴向距离与粒子半径之比。纵坐标是轴向声辐射力。从图7的计算结果可见,粒子距离波束中心越近,轴向声辐射力值越大,当粒子在轴向逐渐远离波源时,轴向声辐射力的值逐渐减小。粒子的声辐射力与粒子到波源的距离成反比关系。
2.3.3 声辐射力与刚性球形粒子横向离轴距离关系
为了研究球形粒子位于声场任意位置处声辐射力的变化规律,对粒子分别在轴向和横向上偏移波束中心不同的距离时轴向和横向声辐射力的变化进行了仿真,计算结果如图8和图9所示。

图8 不同偏移距离下轴向声辐射力与x/a的变化关系Fig.8 The relationship of axial radiation force and different x/a
从图8的仿真结果可见,当刚性球形粒子在轴向距离波束中心的距离不变时,在波束轴上,即x/a=0,轴向的声辐射力值最大。当粒子从波束中心向两侧偏移时,轴向声辐射力随粒子横向偏离波束中心距离的增大而逐渐减小,且在两侧相同横向位置的轴向声辐射力近似相等。当横向距离不变时,轴向声辐射力与轴向距离成反比。仿真结果与文献[13-15]的数值积分计算结果一致。图8中的轴向声辐射力不完全对称是由于时域有限差分算法是将计算区域离散网格化,当向两侧移动球形粒子时,两侧所取的球上网格节点数略有不同,会产生两侧不完全对称的情况,从而使计算结果稍有不同。

图9 不同偏移距离下横向声辐射力与x/a的变化关系Fig.9 The relationship of transverse radiation force and different x/a
图9是横向声辐射力与粒子横向偏移距离的变化关系图,图中的3条曲线分别对应的是轴向偏离波束中心1a、2a、5a的距离时,横向声辐射力随横向偏离波束中心距离的变化关系曲线。从图9的仿真结果可见,刚性球形粒子在波束轴上时,三条曲线的横向声辐射力都近似为0。当粒子从波束中心位置向两侧横向移动,球形粒子受到的横向辐射力大小相等,方向相反。随着偏离波束中心距离的增大,横向声辐射力的值逐渐增大。当球形粒子距离波束中心的距离约为粒子半径的3倍时,力达到最大值。随着偏移的距离继续增大,粒子受到的横向声辐射力开始减小。从图中可见,两侧相同位置的横向声辐射力是一对大小相等,方向相反的力,在相同横向位置处,不同的轴向距离,横向声辐射力的值是不同的,粒子在轴向距离波束中心1a时横向声辐射力最大,在轴向距离波束中心5a时,横向声辐射力最小,横向声辐射力的大小与轴向距离波束中心的距离成反比。
3 结论
本文以声波理论为基础,应用时域有限差分法,结合应力张量方程,计算了离轴高斯波束作用下水中刚性球形粒子的声辐射力。仿真研究结果表明,刚性球形粒子在高斯声场中的声辐射力随着粒子沿轴向偏离波束中心距离的增大而减小。刚性球形粒子位于声场任意位置时,轴向声辐射力与轴向和横向偏移距离的变化成反比关系。横向声辐射力随横向偏移距离的增加是先增大后减小。在波束中心两侧相同距离处,横向辐射力大小相等,方向相反。时域有限差分法是一种简单、直观、适用性广的数值方法,能直观模拟声波与物体相互作用的过程,该研究将为时域有限差分法在不同形状、不同材料的多个粒子间声辐射力的计算提供依据。
[1] Marston L Philip. Negative axial radiation forces on solid spheres and shells in a Bessel beam[J]. Journal of the Acoustic Society America, 2007, 122:3162-3168.
[2] Mitri F G, Silva G T. Off-axial acoustic scattering of high-order Bessel vortex beam by a rigid sphere[J]. Wave Motion, 2011, 48(5):392-400.
[3] Wu Juru, Du Gonghuan. Acoustic radiation force on a small compressible sphere in a focused beam[J]. Journal of the Acoustic Society America, 1990, 87(3):997-1003.
[4] Lee J, Shung K K. Radiation forces exerted on arbitrarily located sphere by acoustic tweezers [J]. Journal of the Acoustic Society America, 2006, 120 (2): 1084-1094.
[5] Lee J, The S Y, Lee A, et al. Single beam acoustic trapping[J]. Applied Physics Letter, 2009, 95: 123-126.
[6] Yee K S. Numerical solution of initial boundary value problems involving Maxwell equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1996, 14(3):302-307.
[7] Cai Feiyan, Meng Long, Jiang Chunxiang, et al. Computation of the acoustic radiation force using the finite-difference time-domain method[J]. Journal of the Acoustic Society America, 2010, 128 (4): 1617-1622.
[8] Cheng Xin, Cai Feiyan, Meng Long, et al. Computation of the acoustic radiation force on a sphere based on the 3-D FDTD Method[C]//2010全国压电和声波理论及器件技术研讨会论文集.厦门:厦门大学, 2010: 236-239.
[9] 黄坤朋,赵越喆. 声学FDTD法完全匹配层数和衰减系数对衰减性能的影响[J].华南理工大学学报:自然科学版,2011,39(4):135-139.
[10] 陈冬梅,张小凤,张光斌,等.水中刚性柱在高斯声场中的声辐射力特性[J].陕西师范大学学报:自然科学版,2014,42(2):27-32.
[11] 陈冬梅,张小凤,张光斌,等.水中球形粒子对高斯波束的声散射[J]. 陕西师范大学学报:自然科学版,2013,41(4):31-34.
[12] 宋智广,张小凤,张光斌.高斯波束对水中柱形粒子的声辐射力研究[J].压电与声光,2013,35(6):792-796.
[13] Wei W, Thiessen D B, Marston P L.Acoustic radiation force on a compressible cylinder in a standing wave[J]. Journal of the Acoustic Society America, 2004,116: 201-208.
[14] Mahdi Azarpeyv, Mohammad Azarpeyvand. Acoustic radiation force on a rigid cylinder in a focused Gaussian beam[J]. Journal of Sound and Vibration, 2013, 332: 2338-2349.
[15] Roumeliotis J A, Agissilaos-Georgios P Ziotopoulos, Kokkorakis G C.Acoustic scattering by a circular cylinder parallel with another of small radius[J]. Journal of the Acoustic Society America, 2001, 109(3): 870-877.
〔责任编辑 李 博〕
Computation of the off-axial acoustic radiation force on a rigid spherical particles via FDTD
SUN Xiuna, ZHANG Xiaofeng, ZHANG Guangbin*, WANG Yan, CHANG Guodong
(School of Physics and Information Technology, Shaanxi Normal University,Shaanxi Key Laboratory of Ultrasonics, Xi′an 710119, Shaanxi, China)
In order to accurately and simply calculate the acoustic radiation force,the FDTD (Finite Difference Time Domain) method is applied to discrete the acoustic wave equations in both spatial and temporal domain. By setting the appropriate boundary conditions, the pressure and velocity are computed by numerical iteration in time domain. The two-dimensional acoustic radiation force on a rigid spherical particle in water is calculated by the momentum-flux tensor equations and the finite difference domain method. The influence of frequence and shift distance from beam center on acoustic radiation force are obtained for rigid sphere particle.The results show that the axial acoustic radiation force decreases with the axial shift distance. When the particle is moved away from the beam axial, the axial acoustic radiation force is reduced. The transverse radiation force is increasing first then decreasing as the shift distance increased.The directions of the transverse force are opposite and the amplitudes of them are same when the particle shifts from the beam center with same distance.Key words: FDTD; Gaussian beam; off-axial acoustic radiation force; numerical simulation
1672-4291(2015)04-0028-06
10.15983/j.cnki.jsnu.2015.04.241
2015-01-24
中央高校基本科研业务费专项资金(GK201302049); 陕西省自然科学基金(2012JM1013)
孙秀娜,女,硕士研究生,研究方向为功率超声。E-mail:819168301@qq.com
*通信作者:张光斌,男,副教授,博士。E-mail:guangbinzhang@snnu.edu.cn
O422.2; TB556
A
