广义可能性计算树逻辑的不动点语义

邓楠轶，张兴兴，李永明

(陕西师范大学 计算机科学学院，陕西 西安710119)

广义可能性计算树逻辑的不动点语义

邓楠轶，张兴兴，李永明*

(陕西师范大学 计算机科学学院，陕西 西安710119)

计算树逻辑的不动点语义在其对应的符号模型检测方法中具有重要意义。给出广义可能性计算树逻辑的不动点语义解释，并利用归纳法证明此不动点为最大或最小不动点。结论表明,广义可能性计算树逻辑的不动点语义具有不同于经典情形的形式。

广义可能性测度；计算树逻辑；不动点语义；模型检测

21世纪的信息技术革命愈演愈烈，随着计算机软硬件系统日趋复杂，如何保证其正确性成为系统设计者和应用者不得不关心的问题。为此提出的诸多验证理论和方法中，模型检测[1-4]因其自动化程度高而引人注目。模型检测是一种形式化的自动验证技术，其基本思想是：对状态空间进行穷举搜索从而验证系统是否满足其设计规范。模型检测的一般步骤是：(1)抽象出系统的数学模型；(2)给出能够描述该系统性质的语言；(3)用模型检测算法进行验证。如果构造的模型满足系统的性质则返回“成功”，否则返回“失败”，并给出反例。

经典的模型检测已广泛应用于软硬件系统的正确性验证，但随着系统日益复杂，在验证过程中不可避免会出现一些不确定的信息，而系统中这些不确定的信息有可能会导致非常严重的后果。为了更好地处理这些不确定信息，一些学者提出了状态迁移模型的量化扩展，比如在状态中加入时间[1]，或者在模型中考虑概率[1]、可能性[5]、多值[6-7]或者统计信息[8]。本文关注李永明等提出的可能性测度下的计算树逻辑的模型检测方法[9-15]。

符号模型检测是1987年由McMillan提出的,其基本原理是将系统的状态转换关系用逻辑公式表示。二叉图(Binary Decision Diagram)是用以表示逻辑公式的重要手段，OBDD(Order Binary Decision Diagram)作为布尔公式的一个规范的表示形式，比一般的传统公式如析取公式及合取公式能够更加紧凑地表示状态转换关系，以降低系统模型所需的内存空间。换言之，它避免了对系统状态的传统表示从而解决状态爆炸问题。符号模型检测的基础是对时序逻辑符的不动点语义解释。本文主要是系统地给出了广义可能性计算树逻辑的不动点语义。

1 预备知识

本节介绍本文用到的一些基本概念，广义可能性Kripke结构及相应的广义可能性计算树逻辑。

1.1 广义可能性Kripke结构(Generalized Possibilistic Kripke Structure ,GPKS)

定义1[13]一个GPKS是一个五元组M(S,P,I,AP,L)，其中

(1)S是一个可数非空状态集合；

(2)P:S×S→[0,1]是可能性转移函数，满足对任意状态s，存在状态t，使得P(s,t)>0；

(3)I:S→[0,1]是可能性初始分布，满足存在状态s，使得I(s)>0；

(4) AP是一组原子命题的集合；

(5)L:S→[0,1]AP是可能性标签函数，将s映射到AP的模糊子集，表示AP在状态s成立的可能性。其中[0,1]AP表示集合AP到单位区间[0,1]上的函数全体构成的集合。

若S和AP是有穷的，则称M是有穷的GPKS。

(2) 可能性转移函数P:S×S→[0,1]可以表示成一个模糊矩阵P，P=(P(s,t))s,t∈S。P也称为M的模糊转移矩阵。

(3)I(s)>0的状态称为初始状态。设s、t∈S，P的传递闭包P+定义如下：P+(s,t)=∨{P(s0,s1)∧…∧P(sk-1,sk)|s0=s,sk=t,sk-1∈S,k≥1}。

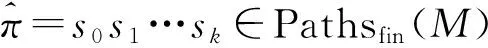
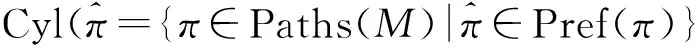
1.2 广义可能性测度

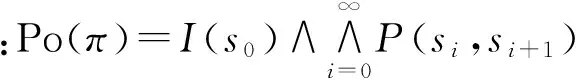
定理1[13]Po是Ω=2Paths(M)上的广义可能性测度，其满足如下条件：

(1) Po(∅)=0；

注2可能性测度[5]除了满足条件(1)和(2)外，还需满足条件Po(Paths(M))=1。

因为本文考虑的GPKSM是有穷的，所以rp(s)可以计算出来，接下来给出一种计算方法。

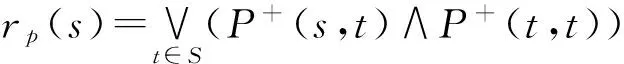
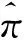
Po(Cyl(s0…sn))=

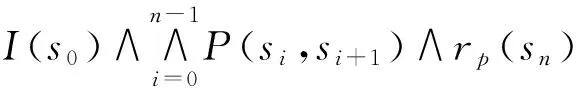
1.3 广义可能性计算树逻辑(Generalized Possibilistic Computation Tree Logic,GPoCTL)

定义4(GPoCTL的语构) GPoCTL的状态公式按如下的BNF形式定义：

Φ∶∶=true|a|Φ|Φ∧Ψ|Po(φ)。

其中，a∈AP，Ψ是状态公式，φ是路径公式。

GPoCTL的路径公式：

φ∶∶=○Φ|Φ∪Ψ|Φ∪≤nΨ|□Φ。

其中，Φ、Ψ是状态公式。

定义5(GPoCTL的语义) 设M是GPKS，s∈S，a∈AP，Φ1、Φ2、Ψ是状态公式，φ是路径公式，那么对于状态公式Φ和状态s，其语义解释是模糊集‖Φ‖:S→[0,1]，递归定义如下：

‖true‖(s)=1;

‖a‖(s)=L(s,a);

‖Φ∧Ψ‖(s)=‖Φ‖(s)∧‖Ψ‖(s);

对路径公式φ，π=s0s1…，π[i…]=sisi+1…，π∈Paths(M)，其语义解释是模糊集‖φ‖:Paths(M)→[0,1]，递归定义如下：

‖○Φ‖(π)=P(π[0,],π[1])∧ ‖Φ‖(π[1]);

‖Φ∪Ψ‖(π)=‖Ψ‖(π[0])∨

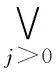
‖Φ‖(π[k]))∧(P(π[j-1],π[j])∧

‖Ψ‖(π[j])));

‖Φ∪≤nΨ‖(π)=‖Ψ‖(π[0])∨

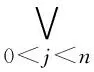
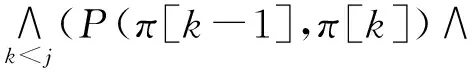
(P(π[j-1],π[j]∧‖Ψ‖(π[j])));

2 GPoCTL的不动点语义

与多值CTL模型检测问题[17]类似，GPoCTL的模型检测问题可以如下描述：

给定一个有穷GPKSM，M中的状态s，GPoCTL状态公式Φ，计算此状态满足公式的程度‖Φ‖(s)。

可以通过对公式Φ的长度|Φ|进行归纳来计算‖Φ‖(s)，|Φ|表示Φ的子公式的数量，定义如下：

如果Φ∈AP∪{true}，则|Φ|=1;

|Φ∧Ψ|=|Φ|+|Ψ|+1;

|Po(○Φ)|=|Po(□Φ)|=|Φ|+1;

|Po(Φ∪Ψ)|=|Po(Φ∪≤nΨ)|= |Φ|+|Ψ|+1。

当Φ=a,Φ,Φ1∧Φ2时，可以直接用语义解释的公式来递归计算出‖Φ‖(s)，但当Φ=Po(φ)时，‖Φ‖(s)=Po(s|=φ)，因此现在的重点是如何计算Po(s|=φ)。由GPoCTL的路径公式知，需分别解决φ=○Φ、φ=Φ∪≤nΨ、φ=Φ∪Ψ和φ=□Φ时的情形。

定理4每个GPoCTL路径公式都可以刻画为一个适当函数的最大或最小不动点形式：

‖Po(Φ∪Ψ)‖=μZ.(‖Ψ‖∧rp)∨ (‖Φ‖∧Po(○Z))

(1)

‖Po(◇Φ)‖=μZ.(‖Φ‖∧rp)∨Po(○Z)

(2)

‖Po(□Φ)‖=υZ.(‖Φ‖∧rp)∧Po(○Z)

(3)

其中(1)、(2)式中μZ.f(Z)表示f(Z)的最小不动点，(3)式中υZ.f(Z)表示f(Z)的最大不动点。

证明(1) 对任何GPoCTL状态公式Φ、Ψ和一个有穷GPKSM，定义函数f(Z)=(‖Ψ‖∧rp)∨(‖Φ‖∧‖Po(○Z)‖))，这里‖Po(○Z)‖=P∘DZ∘rp,DZ是关于向量Z的对角矩阵，f(Z)是从S上的可能性分布的集合到它本身的一个函数。

令Z0=(0,0…0)T是元素全为0的最小向量。定义Zi+1=f(Zi)，因为f是单调的，如果Z′≥Z″，那么f(Z′)≥f(Z″)，因此有上升链Z0≤Z1≤…≤Zi≤Zi+1≤…。

因为Im(Φ)[13]是有穷的，f所涉及的运算不会再产生新的元素，所以Zi的集合是有穷集，因此存在k使得Zk+1=Zk，即f(Zk)=Zk。接下来证明Zk是f的最小不动点。显然，如果Z是f的一个不动点，则Z≥Z0。因为f是单调的，则有Z=f(Z)≥Z1，归纳得Z≥Zk，因此Zk是f的最小不动点。

令A=‖Po(Φ∪Ψ)‖，由语义解释知：

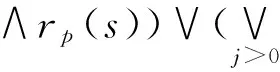
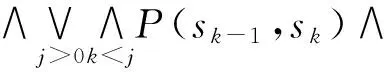
对任何状态s,首先证明A是f的不动点：

f(A)(s)=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧‖Po(○A)‖(s))=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

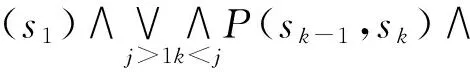
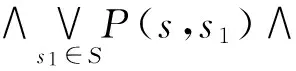
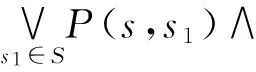
rp(sj))=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧‖Ψ‖(s1)∧rp(s))∨(‖Φ‖(s)∧

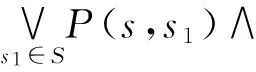
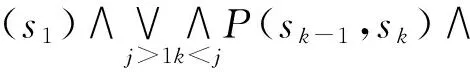
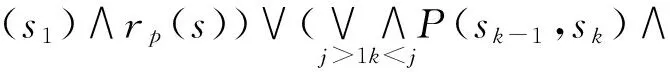
‖Φ‖(sk)∧P(sj-1,sj)∧‖Ψ‖(sj)∧rp(sj))))=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

因此A是f的不动点。

其次,要证明A是f的最小不动点。假设Z是f的一个不动点，即Z=(‖Ψ‖∧rp)∨(‖Φ‖∧‖Po(○Z)‖)=(‖Ψ‖∧rp)∨(‖Φ‖∧P∘DZ∘rp)。令

1) 当j=0时，Z(s)=(‖Ψ‖(s)∧rp(s))∨‖Φ‖(s)，此时A(s)=(‖Ψ‖(s)∧rp(s))∧‖Φ‖(s)。显然，Z(s)≥A(s)。

2) 假设j=n时成立，即有

Z(s)=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

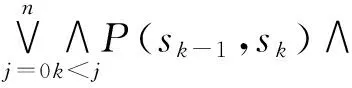
P(sj-1,sj)∧‖Ψ‖(sj)∧rp(sj))∨

P(sj-1,sj)∧‖Ψ‖(sj)∧rp(sj))=A(s)。

3) 则当j=n+1时，有

Z(s)=(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

‖ψ‖(sj)∧rp(sj))∨(‖Φ‖(s)∧

(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

‖Ψ‖(sj)∧rp(sj))∨(‖Φ‖(s)∧

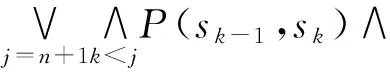
‖Ψ‖(sj)∧rp(sj))∨(‖Φ‖(s)∧

(‖Ψ‖(s)∧rp(s))∨(‖Φ‖(s)∧

‖Ψ‖(sj)∧rp(sj))∨(‖Φ‖(s)∧

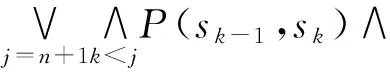
P(sj-1,sj)∧‖Ψ‖(sj)∧rp(sj))=A(s)

综上所述，Z≥A。因此，A=‖Po(Φ∪Ψ)‖是f的最小不动点。

(2) 因为◇Φ=true∪Φ，而‖true‖∧Z=Z，从而有‖Po(◇Φ)‖=μZ.(‖Φ‖∧rp)∨Po(○Z)。

(3) 对任何GPoCTL状态公式Φ、Ψ和一个有穷GPKSM，定义函数f(Z)=‖Φ‖∧‖Po(○Z)‖，这里‖Po(○Z)‖=P∘DZ∘rp，f(Z)是从s上的可能性分布的集合到它本身的一个函数。

令Z0=(1,1…1)T是元素全为1 的最大向量。定义Zi+1=f(Zi)，因为f是单调的，如果Z′≤Z″，那么f(Z′)≤f(Z″)，因此有下降链Z0≥Z1≥…≥Zi≥Zi+1≥…。

因为Im(Φ)[13]是有穷的，f所涉及的运算不会再产生新的元素，所以Zi的集合是有穷集，因此存在k使得Zk+1=Zk，即f(Zk)=Zk。接下来证明Zk是f的最大不动点。显然，如果Z是f的一个不动点，则Z≤Z0。因为f是单调的，则有Z=f(Z)≤Z1，归纳得Z≤Zk。因此Zk是f的最大不动点。

令A=‖Po(□Φ)‖，由语义解释知：

因此，A是f的不动点。

下面要证A是f的最大不动点。假设Z是f的一个不动点，即Z=(‖Φ‖∧rp)∧‖Po(○Z)‖=(‖Φ‖∧rp)∧P∘DZ∘rp,则有

因此Z≤A。表明A=‖Po(□Φ)‖是f的最大不动点。

综上所述，定理4得证。

注3与经典情形下不动点语义[2]相比，上述公式与经典不动点语义形式类似，但是GPoCTL不动点语义形式多交了一个rp，可见rp在广义可能性情形下的重要性。

3 算法及其复杂度分析

在计算定理4中的不动点时，对不动点函数f(Z)的第n次迭代可以计算出从 出发所有长度为n的路径满足Φ的最小或最大上界。因为状态空间S是有穷的，所以如果路径π的长度大于|S|+1，则必然存在一条长度至多为|S|+1的路径π′，使得‖φ‖(π′)≥‖Φ‖(π)或|φ‖(π′)≤‖φ‖(π)，因此不动点的计算在至多|S|+2次后收敛。因为不动点的迭代计算只涉及取大取小运算，所以每次迭代的时间复杂度至多为O(|S|2)，因此计算不动点需要O(|S|3)。

定理5(GPoCTL模型检测不动点算法的时间复杂度)

对于有穷GPKSM，GPoCTL状态公式Φ，GPoCTL模型检测问题M|=Φ的时间复杂度为O(size(M)·poly(|S|)·|Φ|)，size(M)表示模型M的大小，|Φ|表示Φ的子公式的个数。相应的算法如下给出：

算法1：计算不动点

输入：状态集合S上的可能性分布集合到自身的函数f。

输出：f的不动点。

Procedure Fixpoint(x,f)

x′←f(x)

whilex≠x′ do

x←x′

x′←f(x)

end while

returnx

End Procedure

算法2：GPoCTL模型检测不动点算法

输入：GPKSM和GPoCTL公式Φ。

输出：M中∀s∈S，满足Φ的程度‖Φ‖(s)。

Procedure GpoCTLCheck(Φ)

caseΦ

true return (1)s∈S

areturn (L(s,a))s∈S

Φ1∧Φ2return (‖Φ1‖(s)∧‖Φ2‖(s))s∈S

Po(○Φ) returnP∘DΦ∘rp

Po(Φ1∪Φ2)returnFixpoint((0)s∈S,f1)

Po(◇Ф)returnFixpoint((0)s∈S,f2)

Po(□Ф)returnFixpoint((0)s∈S,f3)

Endcase

EndProcedure

其中，P=(P(s,t))s,t∈S，DΦ=diag(‖Φ‖(s))s∈S,rp=P+∘D,P+=P∨P2∨P3∨…∨PN,N=|S|,P*=P0∨P+,P0表示N×N的单位矩阵，

f2(Z)=(‖Ψ‖∧rp)∨(‖Φ‖∧P∘DZ∘rp),

f1(Z)=(‖Φ‖∧rp)∨(P∘DZ∘rp),

f3(Z)=‖Φ‖∧P∘DZ∘rp。

注4GPoCTL模型检测的不动点算法与经典CTL模型检测的不动点算法思想上是一致的，区别在GPoCTL的不动点算法是计算出具体状态公式的取值，而经典CTL的不动点算法是计算出状态公式的满足集Sat(Φ)。

5 结语

本文基于广义可能性Kripe结构，给出了GPoCTL的不动点语义，基于此在对GPKS模型进行验证时，可以利用不动点算法来达到目的。不动点语义完善了现有的广义可能性模型检测理论。

进一步的工作为广义必要性测度下GPoCTL的模型检测不动点语义解释。

[1]BaierC,KatoenJP.Principlesofmodelchecking[M].Cambridge:MITpress, 2008.

[2]ClarkE,GrumbergO,PeledD.ModelChecking[M].Cambridge:TheMITPress,1999.

[3]RozierKY.Lineartemporallogicsymbolicmodelchecking[J].ComputerScienceReview, 2011, 5(2): 163-203.

[4] 林惠民, 张文辉. 模型检测: 理论, 方法与应用[J].电子学报, 2002, 30(12A): 1907-1912.

[5]LiYongming,LiLijun.Modelcheckingoflinear-timepropertiesbasedonpossibilitymeasure[J].FuzzySystems, 2013, 21(5): 842-854.

[6]ChechikM,DevereuxB,EasterbrookS,etal.Multi-valuedsymbolicmodel-checking[J].ACMTransactionsonSoftwareEngineeringandMethodology, 2003, 12(4): 371-408.

[7]FischerE,GradelE,KaiserL.Modelcheckinggamesforthequantitative-calculus[J].TheoryofComputingSystems,2010(47):696-719.

[8]KwiatkowskaM,NormanG,ParkerD.Stochasticmodelchecking[M]∥Formalmethodsforperformanceevaluation.BerlinHeidelberg:Springer, 2007: 220-270.

[9]ZadehLA.Fuzzysets[J].InformationandControl, 1965, 8(3): 338-353.

[10] 李永明. 模糊系统分析[M].北京：科学出版社, 2005.

[11] 王熙照. 模糊测度和模糊积分及在分类技术中的应用[M].北京：科学出版社, 2008.

[12] Li Yongming, Li Yali, Ma Zhanyou. Computation tree logic model checking based on possibility measures[J].Fuzzy sets and Systems, 2015, 262:44-59.

[13] Li Y, Ma Z. Quantitative computation tree logic model checking based on generalized possibility measures[J].DOI:10.1109/TFUZZ.2015.2396537.

[14] 李亚利，李永明.可能性测度下计算树逻辑的若干性质[J].陕西师范大学学报:自然科学版，2013,41(6):6-12.

[15] 李永明.可能LTL模型检测的两种方法[J].陕西师范大学学报:自然科学版，2014，42(6):21-25.

[16] Chechik M, Easterbrook S, Petrovykh V.Model-checking over multi-valued logics[C].Proceedings of FME,2001:72-89.

〔责任编辑 宋轶文〕

Fixed-point semantics of computation tree logic based on generalized possibility measures

DENG Nanyi, ZHANG Xingxing, LI Yongming*

(School of Computer Science, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

Fixed-point semantics of computation tree logic plays an important role in symbolic model checking.Fixed-point semantics of generalized possibilistic computation tree logic is presented, then the greatest or least fixed-point is shown by the method of mathematical induction, which is different from the form in classical model checking.

generalized possibility measures;computation tree logic; fixed-point characterization;model checking

68Q45

1672-4291(2015)04-0022-06

10.15983/j.cnki.jsnu.2015.04.145

2014-12-16

国家自然科学基金(11271237,61228305);高等学校博士学科点专项基金(20130202120001)

邓楠轶，男，硕士研究生，研究方向为模型检测、信息安全攻防。E-mail:nanyideng@gmail.com

*通信作者:李永明,男,教授,博士生导师。E-mail:liyongm@snnu.edu.cn

TP301.2

A