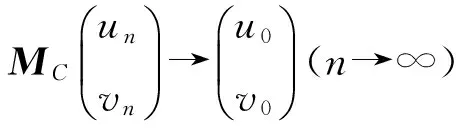
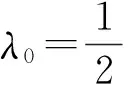上三角算子矩阵的Wely型定理的摄动

张 敏，曹小红，吴学俪

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

上三角算子矩阵的Wely型定理的摄动

张 敏，曹小红*，吴学俪

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

根据给定的两个算子的半Fredholm谱及Weyl谱的结构特点，研究了以这两个给定算子为主对角线的所有的2×2上三角算子矩阵的Browder定理(或Weyl定理)的摄动。给出了2×2上三角算子矩阵满足Browder定理(或Weyl定理)的紧摄动的充要条件。

Browder定理；Weyl定理；紧摄动；谱

1 预备知识

本文中H与K均表示无限维复可分的Hilbert空间，B(H，K)表示H到K上的有界线性算子的全体，记B(H，H)=B(H)，K(H)表示H上的所有紧算子构成的双边理想。对T∈B(H)，令N(T)和R(T)分别表示算子T的零空间和值域。T∈B(H)称为上半Fredholm算子，若R(T)闭且n(T)=dimN(T)有限；特殊地，当n(T)=0且R(T)闭时，称T为下有界算子。T∈B(H)称为下半Fredholm算子，若R(T)闭且n(T*)有限，其中T*表示T的共轭算子。当T∈B(H)为上半或者下半Fredholm算子时，T的指标记为ind(T)=n(T)-n(T*)。当-∞

2 Browder定理(Weyl定理)的摄动

1909年，Weyl[1]在检查Hermitian算子T的谱时发现，T的所有紧摄动的谱集的交集等于其孤立的有限重特征值的全体。这个性质后来被称作为Weyl定理，即算子T∈B(H)满足σ(T)σw(T)=π00(T)其中π00(T)={λ∈isoσ(T):0

设T∈B(H)，对λ∈ρSF(T),T-λI的最小指标定义为

minind(T-λI)=min{n(T-λI),n((T-λI)*)}

为讨论上三角算子矩阵的Browder定理(Weyl定理)的紧摄动，先看几个引理。

引理1设T∈B(H)，则T满足Browder定理的紧摄动当且仅当ρSF(T)仅有一个指标为0的连通分支。

反之，假设ρSF(T)仅有一个指标为0的连通分支Ω。由于对任意K∈K(H),有ρSF(T)=ρSF(T+K),则首先证明对任意的K∈K(H),Ω=ρ(T+K)∪B,其中ρ(T+K)=Cσ(T+K),m(B)=0。因为ρ(T+K)⊆Ω且函数λ→minind(T+K-λI)=n(T+K-λI)在ρSF(T)的每一个连通分支上除去一个至多可数集B后是常值函数(文献[10]，推论1.14)，从而得出Ω=ρ(T+K)∪B，其中m(B)=0。由于σ(T+K)σw(T+K)⊆Ω且m(B)=0，则可证明对任意K∈K(H)，T+K都满足Browder定理。

ρSF(T)仅有一个指标为0的连通分支等价于ρw(T)连通，于是引理1可以叙述为：设T∈B(H)，则T满足Browder定理的紧摄动当且仅当ρw(T)连通。

引理2存在C∈B(K，H)使得2×2上三角算子矩阵MC为Weyl算子的充要条件是A∈B(H)为上半Fredholm算子，B∈B(K)为下半Fredholm算子且下列条件之一成立：

(a)d(A)<∞,n(B)<∞且n(A)+n(B)=

d(A)+d(B);

(b)d(A)=n(B)=∞。

证明必要性很显然。对于充分性，只需要证明当d(A)=n(B)=∞时结论成立即可。为此，分三种情况进行讨论。

(Ⅰ) 设n(A)=d(B)。

因为N(B)和R(A)⊥都可分且维数相同，则存在算子T，满足以N(B)为定义域，以R(A)⊥为值域且对任意y∈N(B)，都有‖Ty‖=‖y‖。定义算子C：K→H为

下面证明MC为Weyl算子。

(1)n(MC)=n(A)<∞。

(2)R(MC)为闭的。

由上面的证明可知MC为上半Fredholm算子。下面只需证明n(MC*)=d(B)=n(A)<∞。

由上面证明可知MC为Weyl算子。

(Ⅱ) 设n(A)>d(B)。

设N(A)=M⊕N，其中dimM=d(B)。令E⊆R(A)⊥满足dimE=dimN<∞。由R(A)⊥为无穷维知,(R(A)⊕E)⊥=R(A)⊥∩E⊥为无穷维的。由于N(B)和(R(A)⊕E)⊥都可分且

n(B)=dim(R(A)⊕E)⊥=∞，

则存在算子T，满足以N(B)为定义域，以(R(A)⊕E)⊥为值域且对任意y∈N(B)，有‖Ty‖=‖y‖。定义算子C:K→H为

下面证明MC为Weyl算子。

(1)n(MC)=n(A)<∞。

由R(C)⊆(R(A)⊕E)⊥=R(A)⊥∩E⊥⊆R(A)⊥，类似于情况(I)中的证明，可证得

n(MC)=n(A)。

(2) 类似于(Ⅰ)，可证得R(MC)为闭的。

由上证明可知MC为Weyl算子。

(Ⅲ) 设n(A)

下面给出文章的一个主要定理。

定理1设A∈B(H),B∈B(K)给定，则任给C∈B(K,H)，MC满足Browder定理的紧摄动当且仅当下列条件成立：

(1)ρw(A)∩ρw(B)连通；

(2)M0满足Browder定理；

(3)F={λ∈C：A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，d(A-λI)=n(B-λI)=∞}=∅。

证明充分性。由引理1，只需证明对任给的C∈B(K,H),ρw(MC)连通。为此需要证明对任给的C∈B(K,H)，ρw(MC)=ρw(A)∩ρw(B)。包含关系ρw(A)∩ρw(B)⊆ρw(MC),显然成立。设λ∈ρw(MC)，则A-λI为上半Fredholm算子，B-λI为下半Fredholm算子,且n(A-λI)+n(B-λI)=d(A-λI)+d(B-λI)。由于F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，d(A-λI)=n(B-λI)=∞}=∅，则d(A-λI)<∞且n(B-λI)<∞。于是M0为Weyl算子。由于M0满足Browder定理，所以A-λI和B-λI均为Weyl算子，即λ∈ρw(A)∩ρw(B)。这样，就证明了对任给的C∈B(K,H),ρw(MC)=ρw(A)∩ρw(B)，所以ρw(MC)连通。由引理1，任给C∈B(K,H)，MC满足Browder定理的紧摄动。

目前各种计算机网络安全问题层出不穷，特别是信息的泄露给用户带来了非常大的负面影响。信息的泄露指的就是用户的一些保密信息被不法分子非法的窃取。随着时代的不断进步和电子技术与各种高端信息技术的快速的发展，随之而来的是人们的各种信息安全无法得到有效的保障。出现这种现象有很多种可能性，比如说内部的资料被偷窃、存储设备意外丢失等。因此现代人的信息安全已经成为不可忽视的一个问题，信息泄露已经直接损害到用户的利益。

∂[σ(A)∪σ(B)]∩ρw(MC0)⊆σ0(A)∪σ0(B)⊆

isoσ(A)∪isoσ(B),

注解1定理1中条件(1)—(3)缺一不可。

(1) 条件“ρw(A)∩ρw(B)连通”是本质的。

1)ρw(A)∩ρw(B)={λ∈C:|λ|<1}∪{λ∈C:|λ|>1|不连通；

2) 由于σ(M0)=σw(M0)=σb(M0)={λ∈C:|λ|=1},则M0满足Browder定理；

3)F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，

d(A-λI)=n(B-λI)=∞}=∅。

于是定理1中条件(1)不满足而条件(2)和(3)均满足。但是由于ρw(M0)={λ∈C:|λ|<1}∪{λ∈C:|λ|>1}不连通，事实上可以证明对任意的C∈B(l1,l1),ρw(MC)={λ∈C:|λ|<1}∪{λ∈C:|λ|>1}均不连通。于是由引理1知任给C∈B(l1,l2)，MC均不满足Browder定理的紧摄动。

(2) 显然,条件“M0满足Browder定理”是本质的；

(3) 条件“F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，d(A-λI)=n(B-λI)=∞}=∅”是本质的。

例如，设A、B∈B(l2,l2)定义为

A(x1,x2,x3,…)=(0,x1,0,x2,0,x3,…),

B(x1,x2,x3,…)=(x2,x4,x6,…),

则

1)ρw(A)∩ρw(B)={λ∈C:|λ|>1}连通；

2) 由于σ(M0)=σw(M0)=σb(M0)={λ∈C:|λ|≤1}，则M0满足Browder定理；

3)F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，d(A-λI)=n(B-λI)=∞}={λ∈C:|λ|<1}≠∅。

{λ0}∪{λ∈C:|λ|>1}⊆ρw(MC)，

{λ∈C:|λ|=1}∩ρw(MC)=∅。

因此，对算子矩阵MC,ρw(MC)一定不连通，则MC不满足Browder定理的紧摄动。

例1设A1、B1∈B(l2)定义为

A1(x1,x2,x3,…)=(0,x1,x2,x3,…),

B1(x1,x2,x3,…)=(x2,x3,x4,…),

(1)ρw(A)∩ρw(B)={λ∈C:|λ-1|>1}∪{λ∈C:|λ+1|>1}连通；

(2) 由于σw(M0)=σb(M0)={λ∈C:|λ-1|≤1}∪{λ∈C:|λ+1|≤1}，则M0满足Browder定理；

(3) 易证F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，

d(A-λI)=n(B-λI)=∞}=∅，

由定理1，任给C∈B(l2,l2)，MC满足Browder定理的紧摄动。

下面讨论算子矩阵的Weyl定理的紧摄动。

定理2设A∈B(H),B∈B(K)给定，则任给C∈B(K,H)，MC都满足Weyl定理的紧摄动当且仅当下列条件成立：

(1)ρw(A)∩ρw(B)连通；

(2)M0满足Browder定理；

(3)F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，

d(A-λI)=n(B-λI)=∞}=∅;

(4) isoσw(M0)=iso[σw(A)∪σw(B)]=∅。

证明设任给C∈B(K,H)，MC都满足Weyl定理的紧摄动，由定理1及文献[13]中定理1.4可知(1)—(4)均成立。反之，只需证明对任意的C∈B(K,H)以及任给紧算子K⊆B(H,K)，π00(MC+K)⊆[σ(MC+K)σw(MC+K)]。若λ0∈π00(MC+K)∩σw(MC+K)，则λ0∈isoσw(MC+K)。由σw(MC+K)=σw(MC)知λ0∈isoσw(MC)。由定理1的证明知任给C∈B(K,H)，σw(MC)=σw(M0)=σw(A)∪σw(B)，于是λ0∈isoσw(M0)。这就与isoσw(M0)=iso[σw(A)∪σw(B)]=∅相矛盾，所以π00(MC+K)∩σw(MC+K)=∅，即π00(MC+K)⊆ρw(MC+K)。因而π00(MC+K)⊆[σ(MC+K)σw(MC+K)]，这样就证明了任给C∈B(K,H)及任给紧算子K∈B(H,K)，σ(MC+K)σw(MC+K)=π00(MC+K)，即MC满足Weyl定理的紧摄动。

对例1中定义的算子A、B，计算得isoσw(M0)=iso[σw(A)∪σw(B)]=∅，于是任给C∈B(l2,l2),MC都是满足Weyl定理的紧摄动。

注解2在定理2中，条件“isoσw(M0)=iso[σw(A)∪σw(B)]=∅”仍然是本质的。

例如，设算子A1、B1、T1∈B(l2,l2)定义为

A1(x1,x2,x3,…)=(0,x1,x2,x3,…),

B1(x1,x2,x3,…)=(x2,x3,x4,…),

(1)ρw(A)∩ρw(B)=C[{-4}∪{λ∈C:|λ-I|≤1}∪{λ∈C:|λ+1|≤1}连通；

(2) 由于σw(M0)=σb(M0)，则M0满足Browder定理；

(3) 易证F={λ∈C:A-λI是上半Fredholm算子，B-λI是下半Fredholm算子，

d(A-λI)=n(B-λI)=∞}=∅;

(4) isoσw(M0)={-4}。

由上面计算可知定理2中的(1)—(3)都满足但是条件(4)不满足。任给C∈B(l2,l2)，计算可知σ(MC)=σw(MC)={-4}∪{λ∈C:|λ-1|≤1}∪{λ∈C:|λ+1|≤1}。

由于N(MC+4I)={0}⊕N(T1)⊕{0}，于是π00(MC)={-4}。显然σ(MC)σw(MC)≠π00(MC)，即MC不满足Weyl定理，于是不满足Weyl定理的紧摄动。

[2] Berberian S K. An extension of Weyl′s theorem to a class of not necessarily normal operators[J].Michigan Mathematical Journal，1969，16(3)：273-279.

[3] Berberian S K. The Weyl spectrum of an operator[J].Indiana University Mathematics Journal，1970，20(47)：529-544.

[4] Coburn L A. Weyl′s theorem for nonnormal operators[J].Michigan Mathematical Journal，1966，13(3)：285-288.

[5] Istratescu V I. On Weyl′s spectrum of an operator I[J].Romanian Journal of Pure and Applied Mathematics，1972，17：1049-1059.

[6] Oberai K K. On the Weyl spectrum[J].Illinois Journal of Mathematics，1974，18(2)：208-212.

[7] Harte R，Lee W Y. Another note on Weyl′s theorem[J].Transactions of the American Mathematical Society，1997，349(5)：2115-2124.

[8] Ji Y Q. Quasitriangular+small compact=strongly irreducible[J].Transactions of the American Mathematical Society，1999，351(11)：4657-4673.

[9] Herrero D A. Economical compact perturbations. II: Filling in the holes[J].Journal of Operator Theory，1988，19(1)：25-42.

[10] Herrero D A. Approximation of Hilbert space operators[M]∥2nd ed.Pitman Research Notes in Mathematics Series，Harlow: Longman Scientific and Technical，1989.

[11] Jiang Z J，Wu Z Q，Ji Y Q. Real function theory[M].3nd ed. Beijing:Higher Education Press，2007：28.

[12] Taylor A E，Lay D C. Introduction to functional analysis[M].New York:Chichester Brisbane Toronto，1980：286.

[13] Li Chunguang，Zhu Sen，Feng Youling. Weyl′s theorem for function of operators and approximation[J].Integral Equations and Operator Theory，2010，67(4)：481-497.

〔责任编辑 宋轶文〕

The perturbation of Weyl type theorem for upper triangular operator matrices

ZHANG Min, CAO Xiaohong*, WU Xueli

(School of Mathematics and Information Science,Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

According to the structure of characteristics of semi-Fredholm spectrum and Weyl spectrum of two given operators, the perturbation of Browder′s theorem (or Weyl′s theorem) for 2×2 upper triangular operator matrices with the two given operators as the main diagonal is researched. The sufficient and necessary condition for operator matrices satisfying the compact perturbation of Browder′s theorem (or Weyl′s theorem) are given.

Browder′s theorem; Weyl′s theorem; compact perturbation; spectrum

47A53,47A10,47A55

1672-4291(2015)04-0010-06

10.15983/j.cnki.jsnu.2015.04.143

2014-10-15

国家自然科学基金(11471200,11371012); 中央高校基本科研业务费专项资金(GK201301007)

张敏,女,硕士研究生,研究方向为算子理论。E-mail:mink.j@163.com

*通信作者：曹小红，女，教授，博士生导师。E-mail:xiaohongcao@snnu.edu.cn

O177.2

A