Hamilton-Jacobi方程的条件Lie-Bäcklund对称和不变子空间

董亚莹，屈改珠，2

(1 西北大学 数学学院，陕西 西安710127；2 渭南师范学院 数学与信息科学学院，陕西 渭南 714000)

Hamilton-Jacobi方程的条件Lie-Bäcklund对称和不变子空间

董亚莹1，屈改珠1，2

(1 西北大学 数学学院，陕西 西安710127；2 渭南师范学院 数学与信息科学学院，陕西 渭南 714000)

利用不变子空间方法和条件Lie-Bäcklund对称研究Hamilton-Jacobi方程。得到方程允许的不变子空间等价于方程的高阶条件Lie-Bäcklund对称。最后给出一些例子构造出Hamilton-Jacobi方程的广义泛函分离变量解。

Hamilton-Jacobi方程；不变子空间；条件Lie-Bäcklund对称；广义泛函分离变量解

文献[1-2]引入了条件Lie-Bäcklund对称方法。条件Lie-Bäcklund对称方法是对非古典对称方法的推广。计算条件Lie-Bäcklund对称的过程和计算非古典对称的过程类似,关键是先给定条件Lie-Bäcklund对称的形式。条件Lie-Bäcklund对称方法是对非线性扩散方程进行对称约化的有效方法之一[3-5],并且还能解释分离变量[6-7]和不变子空间[8]。

本文考虑Hamilton-Jacobi方程

(1)

的条件Lie-Bäcklund对称和不变子空间及其广义泛函分离变量解。该方程可以用于描述非线性扩散方程的长时行为[9-11]。

1 预备知识

下面给出条件Lie-Bäcklund对称的基本定义和命题。令

(2)

是具有特征η的演化向量场,且

ut=E(r,t,u,u1,…,un),t∈R+,r∈R

(3)

是一非线性演化方程,其中

定义1演化向量场(2)称作方程(3)的Lie-Bäcklund对称当且仅当

V(ut-E)|L∩M=0,

其中L表示ut-E=0关于r、t的所有微分序列，M表示η=0关于r的所有微分序列。

命题1[1-2]方程(3)允许条件Lie-Bäcklund对称(2)的充分条件是存在W(t,r,u,η)使得

(4)

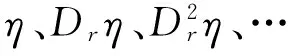
显然,若

Dtη|L∩M=0,

(5)

则方程(3)允许具有特征η的条件Lie-Bäcklund对称。

下面介绍不变子空间方法[12]。一个有限维线性空间

Wl=L{f1(x),f2(x),…,fl(x)}=

如果线性子空间Wl在给定算子F作用下不变,那么方程(3)有广义分离变量解

L[y]=y(l)+al-1(x)y(l-1)+…+a1(x)y′+a0(x)y=0

(6)

L[F[u]]|[H]=0,

(7)

其中[H]表示L[u]=0及其关于x的微分序列。由不变条件(7)知不变子空间与条件Lie-Bäcklund对称有关[4,7-8]。

定理1[12-13]如果方程(6)的解空间定义的l维子空间Wl在一个k阶非线性微分算子F作用下不变,那么l≤2k+1。

现在考虑方程(1)的条件Lie-Bäcklund对称

η=[g(u)]lx+a1(x)[g(u)](l-1)x+…+al(x)g(u)。

(8)

若方程(1)允许条件Lie-Bäcklund对称(8),则

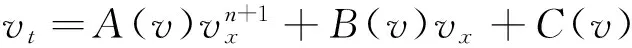
(9)

允许条件Lie-Bäcklund对称

σ=vlx+a1(x)v(l-1)x+…+al(x)v,

(10)

其中

A(v)=(f′(v))n,B(v)=D(f(v)),

C(v)=Q(f(v))/f′(v),

且u=f(v)是v=g(u)的反函数。

2 方程(9)的条件Lie-Bäcklund 对称和不变子空间

研究方程(1)的条件Lie-Bäcklund对称(8)等价于研究方程(9)的条件Lie-Bäcklund对称(10)。条件Lie-Bäcklund对称(10)定义的线性常微分方程σ=0的解空间即为方程允许的不变子空间Wl=L{f1(x),f2(x),…,fl(x)}。

当l=2时,由命题1知,方程(9)允许具有特征(10)的条件Lie-Bäcklund对称的充分条件是

C′a2v+a2C=0,

(11)

其中“′”表示对隐含变量的导数,取上述关于vx的多项式系数为零可得方程(9)及其相应的条件Lie-Bäcklund对称(10)中的未知函数,它们满足下面的决定方程组,即

由决定方程组(12)的第5个式子可得a2(x)=0,并且方程组(12)的第6个式子能得到B(v)=p1v+q1,其中p1、q1是任意实数。下面出现的c、d、ci、di、m、mi、pi和qi也是任意实数。因此,(12)式可以化简为

解上面的常微分方程系统可得

(13)

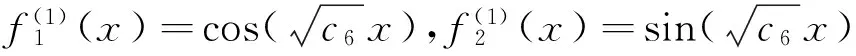
表1 当l=2方程(9)的条件Lie-Bäcklund对称(10)和不变子空间WlTab.1 Conditional Lie-Bäcklund symmetries (10) and invariant subspaces Wl with l=2 of equation (9)

表2 当l=2对某些n方程(9)的条件Lie-Bäcklund对称(10)和不变子空间WlTab.2 Conditional Lie-Bäcklund symmetries (10) and invariant subspaces Wl with l=2 of equation (9) for some special n

表3 当l=3方程(9)的条件Lie-Bäcklund对称(10)和不变子空间WlTab.3 Conditional Lie-Bäcklund symmetries (10) and invariant subspaces Wl with l=3 of equation (9)

3 方程(1)的广义泛函分离变量解

变换v=g(u)不仅将方程(9)允许的条件Lie-Bäcklund对称(10)变换为方程(1)允许的条件Lie-Bäcklund对称(8),还将方程定义在不变子空间Wl=L{f1(x),f2(x),…,fl(x)}上的广义分离变量解v(x,t)=C1(t)f1(x)+C2(t)f2(x)+…+Cn(t)fn(x)变换为方程(1)的广义泛函分离变量解g(u)=C1(t)f1(x)+C2(t)f2(x)+…+Cn(t)fn(x)。这两个解中的未知函数Ci(t)满足有限维动力系统,该动力系统是将广义分离变量解v(x,t)代入方程(9)后取fi(x)左右两边的系数相等而得。下面构造几个例子解释这个过程。

例1方程

(14)

允许的二阶条件Lie-Bäcklund对称是η=vxx。方程(14)建立在不变子空间W{x,1}上的广义分离变量解是v(x,t)=α(t)x+β(t),其中α(t)和β(t)满足下面的二维动力系统:

α′=c1αn+2+p1α2+c1α,

β′=cαn+1β+dαn+1+p1αβ+q1α+c1β+d1。

其中

α(t)和β(t)满足上面的二维动力系统。

例2方程

(15)

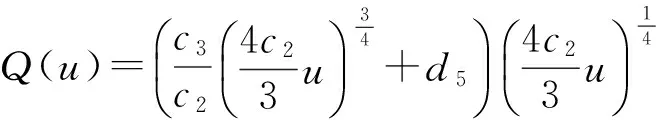
例3方程

(16)

允许的三阶条件Lie-Bäcklund对称是η=vxxx+m5vxxx。该方程相应的广义分变量解是v(x,t)=α(t)+β(t)x+γ(t)exp(-m5x)，其中α(t)、β(t)和γ(t)满足以下三维动力系统

2m5c15βγ2exp(-2m5x)+

m5c16γ2exp(-2m5x)+c17α+

c17γexp(m5x)+d17,

β′=c15β3-2m5c15β2γexp(-m5x)+

m5c16βγexp(-m5x)+c17β,

γ′=-2m5c15αβγ+c15β2γ+c16βγ-c16m5αγ。

其中

例4方程

(17)

允许的三阶条件Lie-Bäcklund对称是η=vxxx。方程(17)定义在不变子空间W{x2,x,1}上的广义分离变量解是v(x,t)=α(t)+β(t)x+γ(t)x2,其中α(t)、β(t)和γ(t)满足动力系统

α′=m6β2+m7β+c18α+d18,

β′=4m6βγ+2mγγ+c18β,

γ′=4m6γ2+c18γ。

4 结论

本文用条件Lie-Bäcklund对称方法对Hamilton-Jacobi方程进行了分类。研究方程非线性条件Lie-Bäcklund对称(8)等价于研究该方程由变换v=g(u)而得的新方程的线性条件Lie-Bäcklund对称(10)。由σ=0和相应方程的相容性构造了分类所得方程的广义分离变量解。这些结果可以由变换v=g(u)转化为非线性扩散方程允许的非线性条件Lie-Bäcklund对称η及其广义泛函分离变量解。这些解可用来刻画方程的长时行为等性态。

[1] Zhdanov R Z. Conditional Lie-Bäcklund conditional symmetry and reductions of evolution equations[J].Journal of Physics A:Mathematical and Theoretical,1995, 28(13): 3841-3850.

[2] Fokas A S, Liu Q M.Nonlinear interaction of traveling waves of nonintegrable equations[J].Physical Review Letters, 1994, 72(21): 3293-3296.

[3] Qu C Z.Group classification and generalized conditional symmetry reduction of thenonlinear diffusion-convection equation with a nonlinear source[J].Studies in Applied Mathematics, 1997, 99(2): 107-136.

[4] Ji L N.Lie-Bäcklund conditional symmetries and functionally generalized separable solutions to the generalized porous medium equationswith source[J].Journal of Mathematical Analysis and Applications,2012, 389(2): 979-988.

[5] 万晖.广义条件对称和变系数非线性扩散方程的解[J].陕西师范大学学报: 自然科学版, 2012, 40(5): 14-17.

[6] Qu C Z, Zhang S L, Liu R C.Separation of variables and exact solutions to quasilinear diffusionequations with nonlinear source[J].Physica D:Nonlinear Phenomena, 2000, 144(1/2): 97-123.

[7] 勾明, 王丽真.非线性反应扩散方程的分离变量解[J].西北大学学报: 自然科学版, 2007, 37(6): 963-965.

[8] Ji L N, Qu C Z.Conditional Lie-Bäcklund conditional symmetries and invariant subspace tononlinear diffusion equation[J].IMA Journal of Applied Mathematics, 2011, 76(4): 610-632.

[9] Galaktionov V A.Geometric sturmian theory of nonlinear parabolic equations and applications[M].Boca Raton:Chapman Hall/CRC, 2004.

[12] Galaktionov V A, Svirshchevskii S R.Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics[M].London: Chapman and Hall, 2007.

[13] Svirshchevskii S R.Lie-Bäcklund conditional symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J].Physics Letters A, 1995, 199(56): 344-348.

〔责任编辑 宋轶文〕

Invariant subspaces and conditional Lie-Bäcklund symmetries of the Hamilton-Jacobi equation

DONG Yaying1, QU Gaizhu1,2

(1 School of Mathematics,Northwest University,Xi′an 710127, Shaanxi, China;2 College of Mathematics and Information Science,Weinan Normal University,Weinan 714000, Shaanxi, China)

Invariant subspace (IS) method and conditional Lie-Bäcklund symmetry (CLBS) are used to study the Hamilton-Jacobi equation.It is proved that the equations admit a class of invariant subspaces,which is equivalent to a kind of higher-order conditional Lie-Bäcklund symmetries of the equations. As a consequence, some examples are given and the generalized functional separable solutions to the Hamilton-Jacobi equation are constructed explicitly.

Hamilton-Jacobi equation; invariant subspace;conditional Lie-Bäcklund symmetry; generalized functional separable solution

35K55;37K05

1672-4291(2015)04-0006-04

10.15983/j.cnki.jsnu.2015.04.142

2014-12-20

国家自然科学基金(11371293);陕西省教育厅基金(14JK1246)

董亚莹,女,博士研究生,研究方向为偏微分方程。E-mail: sxsbjsying@163.com

O175.14

A