随机利率对养老金个人账户的影响分析
2015-06-07王茶香
王茶香
(上饶师范学院 数学与计算机科学学院,江西上饶334001)
随机利率对养老金个人账户的影响分析
王茶香
(上饶师范学院 数学与计算机科学学院,江西上饶334001)
养老金个人账户由于积累时间长,受利率的影响非常大,而利率又是经常变动的,原有的关于养老个人账户利率影响的讨论大都集中在固定利率上,与实际会有很大的偏差。本文把固定利率推广到随机利率,探讨了随机利率对个人账户养老金积累额的影响,更有利于决策者对养老金政策进行决策。
养老金;个人账户;随机利率;维纳过程
随着我国20世纪人口老龄化现象越来越严重,原有的现收现付筹资模式的养老保险体系变得越来越难以为继,在此现状下我国对原有的养老保险制度进行了试点改革,在试点改革成功的基础上建立起了具有中国特色的养老保险制度——社会统筹与个人账户相结合的部分积累制。职工退休后按月领取的养老金由两部分构成:一部分是个人账户养老金(从养老金个人账户中支取)和另一部分是基础养老金(从社会统筹中支取)。制度规定基础养老金的月标准是以当地上年度在岗职工月平均工资和本人指数化月平均缴费工资的平均值为基数,只要缴纳养老金满1年就发给1%,这部分养老金体现了社会保险传统意义上的互济性、分散风险性和社会保障性;个人账户养老金是个人在工作期间缴存的养老金积累额除以制度设计的计发月数所得,这部分养老金强调了职工的自我保障性和激励性(多缴多得)。制度设计之初个人账户养老金大致占了退休后职工所领取养老金约三分之二的比重(从替代率来核算),因此,个人账户养老金的多少对职工退休后的生活有着举足轻重的作用。职工参加工作后个人账户所缴存的养老金通常要经历30至40年时间的积累,这中间个人账户养老金不可避免会面临通货膨胀风险和利率风险。在制度设计时个人账户养老金的记账利率是参考银行同年一年期定期存款利率,银行利率不是一成不变的,而利率的变动对期末付一单位年金的影响如下表所示:

表1 利率、时间对期末付一单位年金的影响
从表1的测算可以看出:期末付1单位的年金,当利率为2%、4%、6%、8%和10%时,经过45年积累比无利率时分别增加了0.6倍、1.7倍、3.7倍、7.6倍、和15.0倍,同时当利率为10%时,只要经过15年该年金就能增加1.12倍,经过35年和45年的积累就能比无利率时增加6.74倍和15.0倍。当利率分别为2%,4%,6%、8%、10%时,经过65年、33年,23年、17年和14年就能比无利率时年金增长一倍,可见利率对年金的影响非常大。个人账户养老金是每个月从工资中扣除一定比例的数额累积而成,所以个仍账户养老金的积累实质就是年金的积累。因此利率对个人账户的影响非常大。业界对个人账户累计值的讨论多是基于固定利率,且多集中在讨论个人账户的替代率问题,而利用随机利率对养老金个人账户进行分析的比较少,如:常彩利用MA(q)模型对个人账户养老金替代率进行了探讨,但从中央银行公布的数据来看,从1990到2014年的25年间利率一共变动了31次,变动幅度从最高的10.08%到最低的1.98%,变动幅度非常大,变动频率也很快,基本上每年平均要变动一次以上。因此建立随机利率模型对个人账户养老金累积额进行讨论,具有较高的理论价值和实践价值。
1 模型的建立






设R(t)=δt+λW(t),其中W(t)为所取定的随机过程,λ为参数,当λ=0时,利率为固定利率。随机过程W(t)可为维纳过程,高斯过程与Poisson过程等,当λ不等于零时,称其为随机过程函数,在利息力累积函数中引入了随机过程,此时个人账户的累积值就称为随机利率下的精算模型。
现代资本市场理论认为利率变化具有随机性特征,现实情况也如此,这里所说的利率随机性特征(马尔科夫性)是指无记忆性,即过去利率不会对未来利率产生任何影响,而一般的金融数学文献大多以布朗运动来对随机利率进行刻画,所以本文也就在布朗运动的基础上建立个人账户的累积值的精算模型。
设利息力函数随机变量为R(t)=δt+λW(t) 0t,其中W(t)为标准维纳过程,δ,λ≥0均为常数,其中δ是常数利息力,λ为参数。
标准维纳过程W(t)具有以下性质:[3]
(1)有限维维纳过程分布为正态分布
(2)维纳过程具有马尔科夫特征;
(3)均值函数m(t)=E(W(t))=0,自相关函数R(t1,t2)=min(t1,t2)
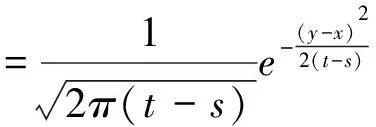
由上面的讨论可知Zi=eR(n-i+1)-R(n-i)则
Ln(Zi)=R(n-i+1)-R(n-i)=δ+λ[W(n-i+1)-W(n-i)] 可得出
从上式可知随机变量Ln(Zi)服从参数为δ和λ2的对数正态分布即Ln(Zi)~N(δ,λ2),
则有:
所以个人账户养老金累积值为
以上将布朗运动引入利息力累积函数,进而构建了随机利率以布朗运动建模的个人账户养老金累积值精算模型。利用上述表达式可以计算个人账户养老金的累积值,与以往固定利率下的个人账户养老金累积值相比,随机利率模型具有抗利率变化的特性,具有实用性。以上的随机过程W(t)还可以用高斯过程或是其他随机过程来替代,可以得到其他的随机利率模型的个人账户养老金累积函数。
2 算例
设某参保人开始缴纳养老金时以工资的100%为缴纳基数,缴费比例为现行社会上统一的所领取工资的11%即c=0.11,每年工资增长比例为10%即g=0.10,参加工作时年薪为w,随机过程中参数取δ=0.05或0.02,λ=0或0.1或0.2,利用上述改进的公式计算出各年个人账户养老金的累积值如表2所示。
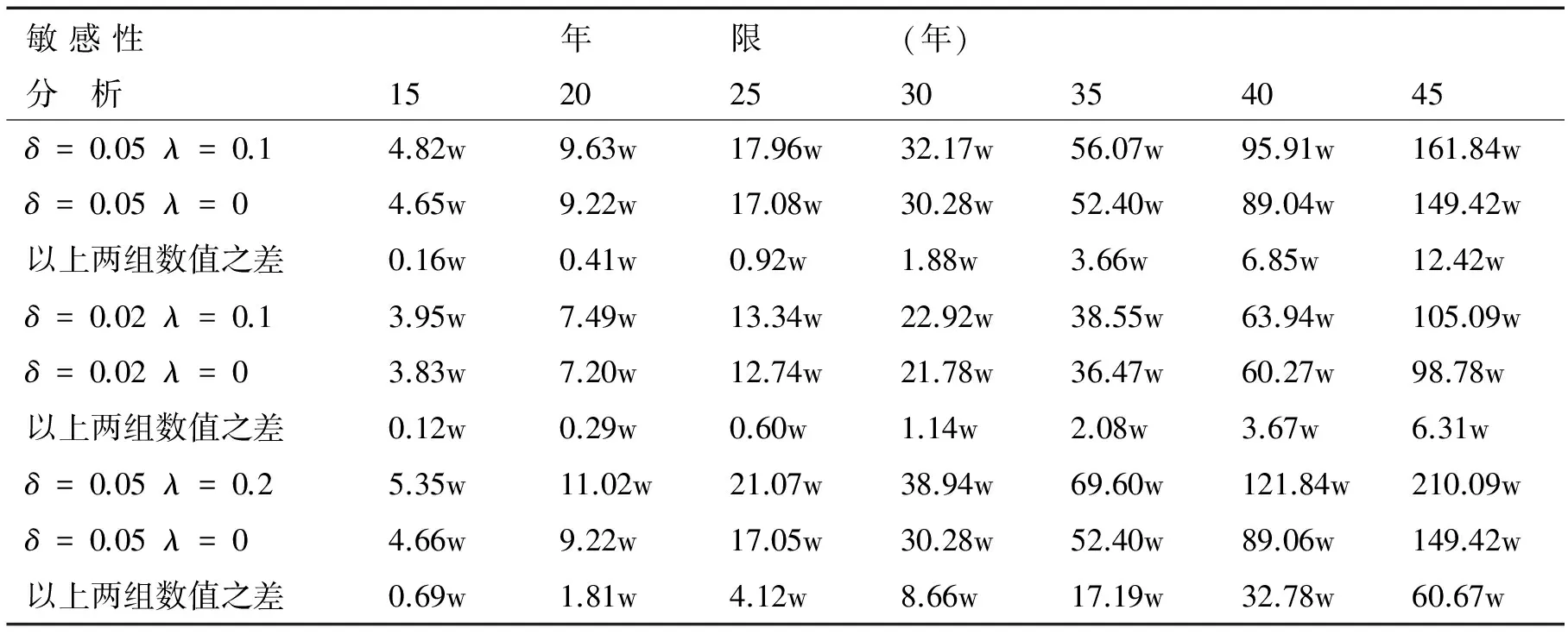
表2 不同参数下养老金个人账户的累积值
从以上的测算可以看出,相同条件下随机利率模型比固定利率模型计算出来的养老金个人账户积累值要大,在随机利率函数所占比重相同的条件下,固定利率越大随机利率与固定利率积累值之差越来越大;随机利率相同的条件下,随着固定利率的增大两者的差距也在增大,比如同样积累35年,当固定利率为5%,λ=0.1和λ=0.2时养老金个人账户两种利率模型核算出的累积值差距为3.66w和17.19w;扩大了将近5倍,当λ=0.1时,固定利率为2%和5%时,两者的差距由原来的2.08w扩大到3.66w,数值增大了将近2倍。
3 结论
在市场经济条件下,利率处于不断变化中,利用随机利率模型对养老金个人账户进行测算更符合实际,也更贴近现实。利用随机利率模型计算的个人账户累积值比固定利率模型计算出来的养老金个人账户累积值要大,差距随着固定利率的增大一直在增大,这种差距也随着积累时间的延长而增大。当积累时间达到30年时,固定理论和随机利率下,养老金个人账户的积累值可以差距将近9年的工资额。现实生活中银行一年期利率是经常变动的,而个人账户养老金的记账利率就是参考同期一年期定期利率,一般职工在职期间至少工作30年退休,也即个人账户养老金的累积也至少有30年,因此利用随机利率核算个人账户养老金的积累值比用固定利率核算更有利于决策者进行决策。
[1]许道军,李文军,李文涛.随机利率下的期初付n年期确定年金[J].淮北煤炭师范学院学报(自然科学版),2009(3):35-37.
[2]刘占国. 利息理论[M].天津:南开大学出版社,2008
[3]贾念念.基于随机利率及死亡率计算改进的寿险精算模型.[M].哈尔滨:哈尔滨工程大学出版社,2012.
[4] 常彩.利率MA(q)模型下个人账户养老金替代率精算模型[J].劳动保障世界,2013,(5):17-18.
[5]王丽燕,杨德礼.一类随机利率下的确定年金[J].数学的实践与认识,2005,(12):8-14.
[6]王丽燕,冯思民.随机利率下的年金的计算[J].运筹学学报,2004,(1):42-50.
[7]王传玉.一类随机利率下的增额寿险[J].运筹与管理,2005,(2):1-10
[8]高建伟.随机利率下的生存年金模型[J].系统工程理论与实践,2002,(6):64-68.
[9]BoylePP.Ratesofreturnasrandomvariables[J].JournalofRisksandInsurance.1976,43(4):693-773.
[10]BeekmanJA,FuellingCP.Interestandmortalityrandomnessinsomeannuities[J].Insurance:MathandEcon,1990,9(2):185-196.
Analysis of the Impact of Stochastic Interest Rates on Individual Pension Accounts
WANG Cha-xiang
( School of Mathematics & Computer Science, Shangrao Normal University, Shangrao Jiangxi 334001,China)
Since the money in individual pension accounts will accumulation for a long time, so the balance of the pension account is significantly affected by interest rates. However, the rates change frequently. While most previous researches emphasize on the influence of fixed interest rates on individual pension accounts, this paper analyzes the impact of stochastic interests rates on individual pension account balance, which is conducive for decisions-makers to make pension policies.
pension;individual accounts;stochastic interest rates;wiener process
2015-11-26
王茶香(1970-)女,江西上饶人, 副教授,硕士,主要研究方向:应用数学、保险与精算。E-mail:wcx197198@163.com
F842.67
A
1004-2237(2015)06-0006-04
10.3969/j.issn.1004-2237.2015.06.002
