共同空间模型及其在EEG分类中的应用

郑国正， 陈李胜

(1.上饶师范学院 计算机网络中心，江西上饶334001；2.北京师范大学 系统科学学院，北京100875)



共同空间模型及其在EEG分类中的应用

郑国正1， 陈李胜2

(1.上饶师范学院 计算机网络中心，江西上饶334001；2.北京师范大学 系统科学学院，北京100875)

通过与传统模型的比较，阐述了共同空间模型及其优势所在，指出其应用方向，最后通过对EEG(Electroencephalograph，脑电波)的实际应用结果分析，验证了共同空间模型在处理非周期性随机信号二分类问题方面的有效性。

共同空间模型；傅里叶变换；EEG；分类

在统计模式识别领域，需要分析处理的对象通常是一个多维的信号数据，对应着一个多维的特征空间。然而真正有用的信息往往只是其中的一部分，而且原始数据的信息冗余度较大，各维数据信号之间又存在较大的相关性。因此在特征提取时，数据的压缩与转化非常重要，有许多方法都是寻求以最小的信息损失来降低特征空间的维数。通过与经典的傅里叶展开和K-L展开相比较，可以看出，共同空间模型在处理二分类问题中的独特优势。

1 传统模型的缺陷

1.1 傅立叶级数展开

因傅里叶的基为正弦函数序列，有很好的正交性，故得到的傅里叶系数都具有很好不相关性。假设一个周期的平稳随机过程x(t)可用傅里叶级数表示如下：

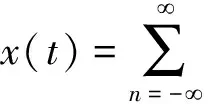
由该式表明，当n≠m，则傅里叶系数互不相关，且x(t)第n个随机傅里叶系数之方差，与R(τ)第n个傅里叶系数两者相等。若研究对象为非周期性的随机序列，则其相关函数即不能以x(t)之傅里叶系数的方差来表示。

1.2Karhunen-Loeve展开

由上一节讨论可知，对于一个非周期性的随机过程，傅里叶级数展开难以胜任，无法表示，但可采用Karhunen-Loeve展开，也就是K-L展开来表示。

设有一非周期性随机过程x(t)，它在区间[a,b]中展开为

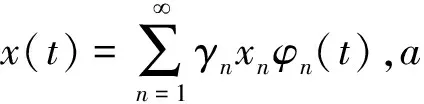
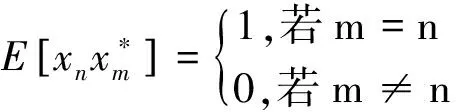
而对于离散情况下的K-L展开，可用最小均方误差准则进行讨论。假设某一向量集合为{xi},i=1,2,...，其每个向量皆以确定的完备正交归一向量系uj,j=1,2,...,进行展开，如此可得：

若以有限项来估计x，即

由此引起的均方误差为：

令Ψ=E[xxT]，则

用拉格朗日乘子法，令

对uj,j=d+1,...,求导数，则 (Ψ-λjI)uj=0,j=d+1,...,

当d=0，则有：矩阵为Ψ=E[xxT]，以其本征向量做坐标轴对原序列进行展开，则其截断误差会具有极值性质，而且若用d个uj,j=1,2,...,d来逼近x时，均方误差：

因此，当以上述矩阵Ψ=E[xxT]中d个最大本征值所对应之本征向量，对某一随机过程x进行展开时，它的截断均方误差可以获得一个最小值，比较对象是在其它所有正交坐标系下用d个坐标对x进行展开所得到的均方误差。

K-L展开具有一个重要性质，即其展开系数相互无关，且K-L的坐标系将Ψ矩阵对角化。也即是说，因为采用了K-L展开，使原有向量的各分量之间，其相关性得以消除，由此带给我们一个可能，即把其中携带信息较少的坐标轴去掉，强化有用信息，从而达到降维的目的。如图1所示。

2 共同空间模型及其优势

从上述讨论中可以看到，K-L展开可以起到对多维信号降维的作用，在一般的特征提取中有很多的应用，因此很多的模式识别领域都用到了这种思想。由于K-L变换时按照特征值的大小排列，也被称为主成分分析。K-L变换虽然是提取了主要特征，但是在有些情况下K-L变换对模式识别中的特征提取并非是最优的，会有特征欺骗现象发生，导致分类结果的误差。如图2所示。

共同空间模型的终极目标即找到对两个类别来说区分度最高的子空间。共同空间模型尤其适合用于解决二分类问题，其原理就是要构建一空间滤波器，找到一个最佳投影，通过该投影，使其中一类信号在某一方向上方差最大，与此同时，另一类信号在该方向则方差最小，由此使得两个类别的差距放大。在数学方面，共同空间模型通过对两类信号协方差矩阵进行同时对角化加以实现[1-2]。

图1 通过K-L变换消除原向量各分量之间的相关性图2 K-L变换在模式识别中的误差

假设XA和XB(N×T)分别是两类大脑模式下产生的脑电信号，共有N个通道和T个样本点。 则两类信号的协方差为：

在此我们假设E(X)=0, 也就是X是零均值的信号。其中XT为X的转置矩阵，原信号XA和XB可以认为是由两个源组成的信号，差异部分Ca、Cb和共同部分Cc，因此信号可以表示为：

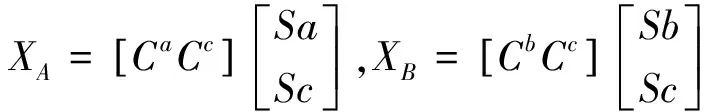
其中Ca是由ma个空间模式(列向量)组成，这些空间模式对应着类别一，同理Cb由mb个空间模式组成。Cc对应了两类的共同模式。这些空间模式描述了信号源到头皮电极的拓扑结构。Sa、Sb、Sc代表了类别A、B的各自信号源和共同信号源，最后求解的目标就是寻找CaSa或是CbSb的最佳估计。

计算方法：

步骤一：对角化RA和RB之和R，得出特征值和特征向量。

步骤二：构造白化矩阵P

步骤三：转换RA和RB

Sa=P·RA·PT,Sb=P·RB·PT

步骤四:SA和SB对角化，

SA=U·ΣA·UT,SB=U·ΣB·UT

SA和SB有共同的特征向量，并且满足ΣA+ΣB=Ι，因此，假设特征值∑是按降序排列的，那么较大的特征值对应的模式代表了类别A的主要特征，较小的特征值对应着B的主要特征。根据这个原则选择特定的空间模式构造滤波器，就可以在二分类问题中提取出两分类中最大差异的子空间，对于第一类别方差最大，而对于另一类别的方差最小，提高模式识别的效率。

3 共同空间模型应用

早在1990年，共同空间模型即被用于对脑电信号分析处理，首开历史先河的是Koles和Coworkers，他们将该方法用于对正常脑电信号及异常脑电信号的区分，从中找出异常因子，进而找到产生异常的原因。之后，更多的是被用于脑机接口(BrainComputerInterfaces，BCI)[2,3]，在此过程中验证了共同空间模型对于二分类问题是有效的。共同空间模型用于单次运动想象分类中取得很好的分类效果(HerbertRamoser2000)，于2003年举办的第二届脑机接口大赛上，荣获冠军的代表队清华大学队，他们所采用的方法就是以共同空间模型为基础的CSSP方法，比赛成绩为超过80%的准确率[2]。在之后的脑机接口竞赛中，共同空间模型应用于多种运动想象分类[4]。

对于脑电信号的检测，往往采用多通道方案，每一通道独立接收一个随机信号，对这类信号的分类，因得益于它的降维能力，共同空间模型的分辨率很高。普通人的脑电信号差异不是很明显，有一特殊群体，就是癫痫病患者，他们在正常状态与发病状态下脑电信号有较大差异，其脑电信号可分为常态时的正常脑电波和病态时的异常脑电波，该问题属于较为典型的二分类问题。采用共同空间模型方法对之进行分析处理，可以很好区分这两种脑电信号，明确判定正常脑电与异常脑电信号，并且以共同空间模型为基础构建的癫痫预测系统，通过对征兆脑电波的寻找，能够在一定程度上对患者做出从正常状态到发病状态的预判，也就是对癫痫病患者作出发病预测[5]。

4 结语

从上述讨论分析可知，对于一个非周期性的随机序列，无法以傅里叶级数展开来表示。采用K-L展开虽然可以，但因为它的特征提取并非最优，存在特征欺骗现象从而导致分类结果误差较大。研究对象诸如脑电信号，往往是多通道非周期性随机信号，在区分正常脑电和异常脑电信号时，采用共同空间模型方法可以很好达成目标。综上可知，共同空间模型对分析处理非周期性随机信号二分类问题表现出了明显优势。

[1]GigolaS,OrtizF,D’AttellisCE,SilvaW,KochenS.Predictionofepilepticseizuresusingaccumulatedenergyinamultiresolutionframework[J].JournalofNeuroscienceMethods2004, 138: 107-111.

[2]LeiX,YangP,XuP,LiuTJ,YaoDZ.Commonspatialpatternensembleclassifieranditsapplicationinbrain-computerinterface[J].JournalofElectronicScienceandTechnologyofChina, 2009, 7:17-21.

[3]DruryI,BeydounA.Interictalepileptiformactivityinelderlypatientswithepilepsy[J].ElectroencephalographyandClinicalNeurophysiology, 1998,106: 369-373.

[4]WangY,BergP,SchergM.Commonspatialsubspacedecompositionappliedtoanalysisofbrainresponsesundermultipletaskconditions:asimulationstudy[J].ClinicalNeurophysiology, 1999,110:604-614.

[5]郑国正,陈李胜,张守文,徐翠萍,韩战钢.基于共同空间模型的癫痫脑电检测预测的优劣[J].北京师范大学学报(自然科学版),2013,(4):430-437.

Common Space Modeling in EEG Classification

ZHENG Guo-zheng1, CHEN Li-sheng2

(1.Computer Network Center of Shangrao Normal University, Shangrao Jiangxi 334001, China； 2.School of Systems Science of Beijing Normal University,Beijing 100875, China)

This study compares Common Space Modeling with a few traditional signal analysis approaches such as the Fourier Transformation.The advantage of the Common Space Modeling is put forward by applying it to EEG signal classification.

common space modeling; Fourier transformation; EEG; classification

2015-11-13

郑国正(1965-)，男，江西上饶人，副教授，硕士，目前主要从事计算机应用研究。E-mail:zgz11@sina.com

R742.1

A

1004-2237(2015)06-0010-04

10.3969/j.issn.1004-2237.2015.06.003