矩阵分离度的新上界

罗红娟，李耀堂

(云南大学 数学与统计学院，云南 昆明 650091)

矩阵分离度的新上界

罗红娟，李耀堂*

(云南大学 数学与统计学院，云南 昆明 650091)

研究了矩阵分离度的上界估计问题，得到了两个新的上界，改进了近期文献中的相应结果，并用算例对所得理论结果进行了说明。

矩阵;特征值;分离度;上界

矩阵的数值特征是矩阵的重要性质，有着广泛的应用背景，一直以来是人们研究的热点问题。1956年Mirsky在［1］中给出了矩阵特征值之间最大距离的定义，称其为矩阵A的分离度(spread)，并给出了矩阵的分离度的两个上界。由于矩阵的分离度在组合优化中的重要应用，随后被人们关注和研究，相继取得了一些有意义的结果。

记Cn×n为所有n×n阶复矩阵所构成的集合，In为单位矩阵。设A=(aij)∈Cn×n，分别记ρ(A)，r(A)，‖A‖F，trA，σ(A)为矩阵A的谱半径、秩、F－范数、迹和谱。将矩阵A进行分块为如下形式

为了方便将Ak×k，Bk×(n－k)，C(n－k)×k和D(n－k)×(n－k)分别简写为Ak，Bk，Ck和Dk。

2012年Wu，Zhang和Liao在［2］中给出了矩阵分离度的三个上界:

2013年R.Sharma，R.Kumar在［3］中对(1)，(2)两式进行了改进，给出了矩阵分离度的两个新上界:

以及

同年，Zhang，Yang在［4］中给出了矩阵分离度的三个上界，其中(7)式和(8)式分别是(4)式和(5)式的改进。

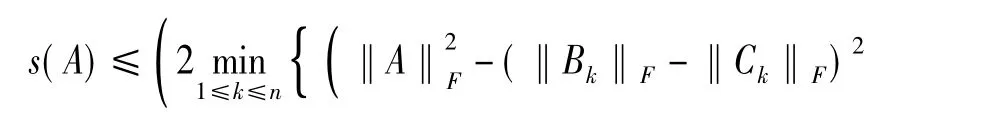
其中l=min{r(A)+1，n}，

这里我们记A(n)=A，Bn=0，Cn=0。

本文继续矩阵分离度上界的研究，给出其两个新的上界估计式，它们分别是(4)式、(7)式和(9)式的改进。

1 预备知识

本节我们给出几个重要引理，以备后用。

引理1.1［5］设A∈Cn×n，若λ1，…，λn是A的n个特征值，则

引理1.2 设A∈Cn×n，且有如(1)的分块形式，若λ1，…，λn是A的n个特征值，则

证明:当‖Bk‖F‖Ck‖F≠0，令

故A和A(k)相似，因此λ1，λ2，…，λn也是A(k)的特征值。

当‖Bk‖F‖Ck‖F=0时，不失一般性假设‖Ck‖F=0。对于矩阵Ak，Dk，由Schur酉三角化定理知，存在酉矩阵U1∈Ck×k和U2∈C(n－k)×(n－k)，使得

所以矩阵A和A(k)有相同的特征值。

由上面讨论知λ1，λ2，…，λn也是矩阵A(k)的特征值，将引理1.1应用到A(k)得

再由k(1≤k≤n－1)的任意性即得(10)式成立。

引理1.3［6］设A∈Cn×n有如下分块形式:

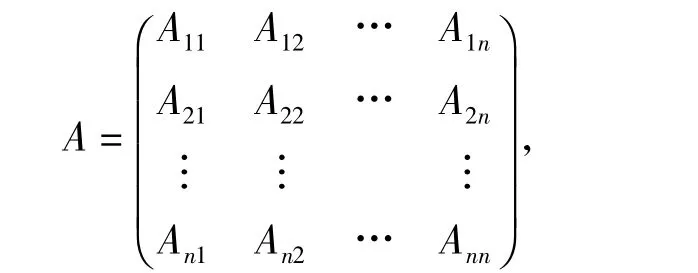
那么

2 矩阵分离度的新上界

下面，我们给出矩阵分离度的两个新上界。

定理2.1 设矩阵A∈Cn×n，且有如(1)的分块形式，则

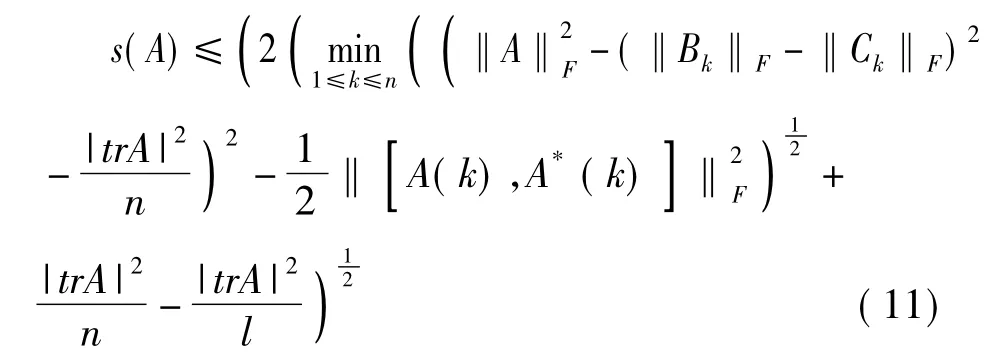
其中，l=min{r(A)+1，n}。

证明:首先证明不等式

设λ1，λ2，…，λn是矩阵A的所有特征值。下面分两种情况进行证明:

(Ⅰ)当r(A)+1=n+1时

于是由拉格朗日恒等式得

因此

(Ⅱ)当r(A)+1≤n时，设λ1，λ2，…，λm是矩阵A的所有非零特征值。若m≥2，根据拉格朗日恒等式以及(Ⅰ)的证明过程有

又因为m≤r(A)，故

所以

由上式得

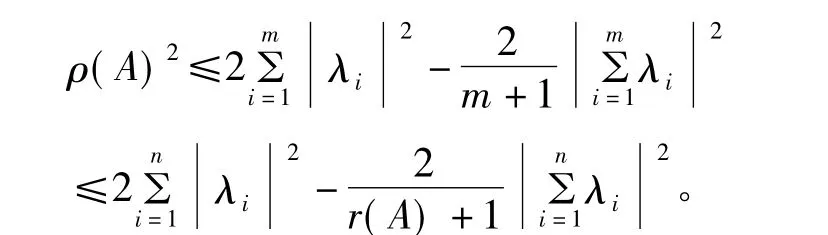
因此

即(12)式成立。由(12)式和引理1.2即得

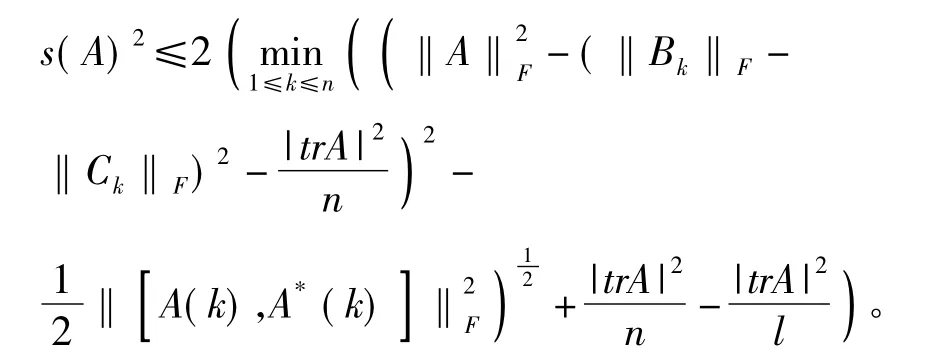
故有

注2.1:因为

所以

由此知

再由引理1.2和(12)式得

此不等式表明定理2.1的(11)式所给上界优于(9)式所给上界。

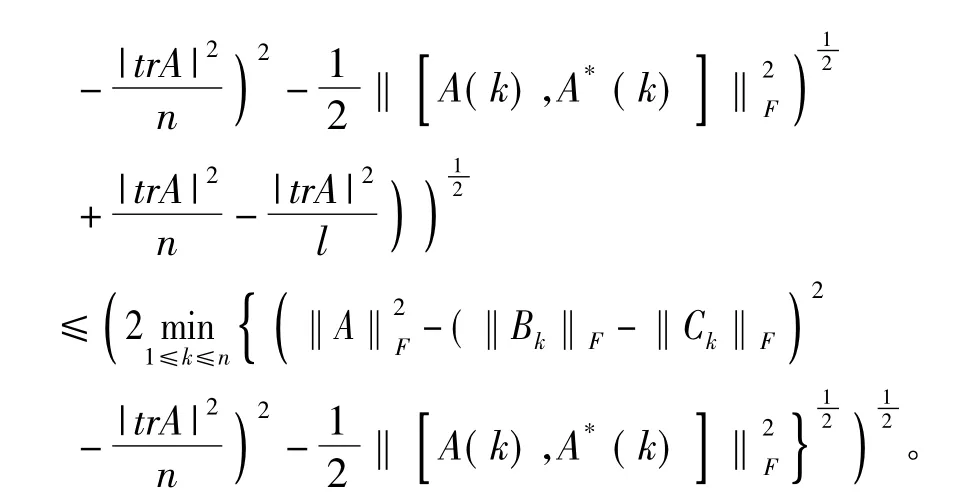
此不等式表明定理2.1的(11)式所给上界优于(7)式所给上界。

下面给出矩阵分离度的另一个上界，它是对(4)式的改进。

定理2.2 设A∈Cn×n有如下分块形式:

则

其中

证明:因为

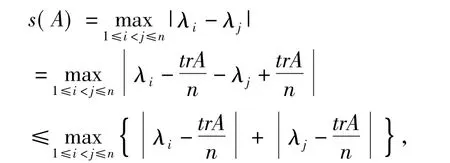
于是由引理1.3得

3 数值算例

本节给出两个数值例子说明本文结论的有效性。

例3.1 设

表1 定理2.1与文［4］结果比较表

从表1知，当矩阵的迹为零时(矩阵A)，(7)，(9)及定理2.1的(11)为同一个估计式，所以它们的估计结果一样。当矩阵的迹不为零但r(A)=n－1时(矩阵B)，(7)式和定理2.1的(11)的估计式是一样的，此时由定理2.1的(11)和(7)式得出的估计结果要比由(9)式得出的估计结果好。但当前面两种情况都不满足时(矩阵C)，定理2.1的(11)比由(7)，(9)所给的结果都好。

例3.2 设

对于矩阵A，应用文［2］的估计式(4)所得的估计结果为s(A)≤16.3118，而应用定理2.2的(13)式所得的估计结果为s(A)≤10.0516。由此知在某些情况下定理2.2的(13)式的估计结果要优于文［2］的估计式(3)的估计结果。

［1］Mirsky L.The spread of amatrix［J］.Mathematika，1956，3 (2):127－130.

［2］Wu J L，Zhang P P and Liao W S.Upper bounds for the spread of a matrix［J］.Linear Algebra Appl，2012，437 (11):2813－2822.

［3］Sharma R and Kumar R.Remark on upper bounds for the spread of amatrix［J］.Linear Algebra Appl，2013，438(11) :4359－4362.

［4］Zhang PP and Wu Y.Improvements in the upper bounds for the spread of amatrix［J］.Mathematical Inequalities＆Applications，2015，18(1):337－345.

［5］Huang T Z and Wang L.Improving bounds for eigenvalues of complex matrices using traces［J］.Linear Algebra Appl，2007，426:841－854.

［6］廖辉.矩阵特征值的一个改进结果［J］.西南大学学报(自然科学版)，2013，35(6):46－49.

［责任编辑 毕 伟］

New Upper Bounds of the Spread of A M atrix

LUO Hong－juan，LIYao－tang*

(School of Mathematics and Statistics，Yun'nan University，Kunming 650000，China)

Estimations of upper bound of the spread of amatrix is researched，tow new upper bounds of the spread of amatrix，which improve the corresponding results in recent literatures，are obtained，and the theoretical results are illustrated with examples.

matrix;eigenvalue;spread of amatrix;upper bound

O151.21

A

1004－602X(2015)03－0001－05

10.13876/J.cnki.ydnse.2015.03.001

2015 -04 -16

国家自然科学基金资助项目(11361074)

罗红娟(1989—)，女，陕西咸阳人，云南大学在读硕士研究生。 *为通讯作者