椭圆曲线y2=x3－21x－90的正整数点

李亚卓，崔保军

(1.陕西学前师范学院 学报编辑部，陕西 西安 710061;2.甘肃民族师范学院 数学系，甘肃 合作 747000)

椭圆曲线y2=x3－21x－90的正整数点

李亚卓1，崔保军2

(1.陕西学前师范学院 学报编辑部，陕西 西安 710061;2.甘肃民族师范学院 数学系，甘肃 合作 747000)

利用四次Diophantine方程的已知结果，运用初等数论的方法证明了椭圆曲线y2=x3－21x－90仅有正整数点(x，y)=(6，0)。

椭圆曲线;四次Diophantine方程;正整数点

设N+是全体正整数的集合。近年来，对于寻找椭圆曲线的整数点的问题引起了人们广泛的兴趣，这方面的成果也有着广泛的应用［1，2］。1987年，Zagier［3］提出了椭圆曲线

的整数点问题。2009年，祝辉林和陈建华［4］运用代数数论的P－adic分析方法证明了椭圆曲线(1)仅有整数点(x，y)=(2，0)和 (28844402，± 154914585540)。2010年，吴华明［5］运用Pell方程和二元四次Diophantine方程的一些已知结果，给出了上述结论的一个简洁证明。2014年，管训贵［6］对运用初等数论的方法给出了(1)的一种推广形式的整数点。本文运用同余等初等方法得到以下结论。

定理 对于奇素数p，椭圆曲线

仅有正整数点(x，y)=(6，0)。

1 引理

引理1［7］丢番图方程y2=Dx4+1在D=348时无正整数解。

2 定理的证明

设(x，y)是(2)的解，从(2)可得

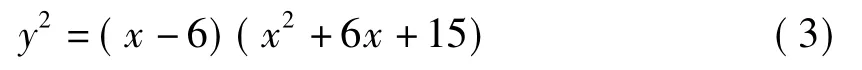
因为x2+6x+15=(x+3)2+6＞0，所以从(3)可知x≥6。当x=6时，由(3)可知(2)有整数点(x，y)= (6，0)。故以下仅需考虑x＞6且y≠0时的情况。

设d=gcd(x－6，x2+6x+15)，易知d|87。故有d∈{1，3，29，87}。以下分四种情况进行讨论:

当d=1时，从(2)可知

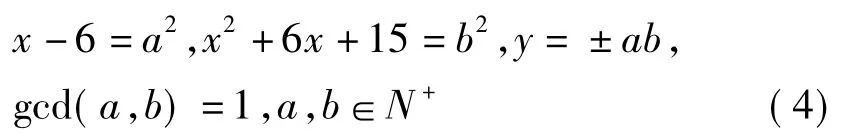
从(4)中第二个等式得(x+3)2+6=b2，知

x+3≡b(mod2)，但此时可得2≡b2－(x+3)2≡0(mod4)。矛盾。

当d=3时，从(2)可知

从(5)可得

当d=29时，从(2)可知

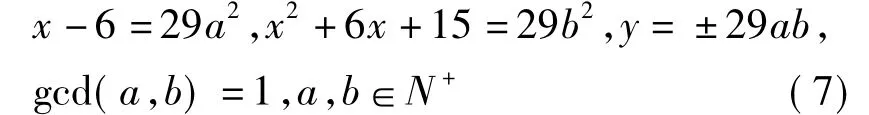
从(7)可得

当2|a时，从(8)可知3a2+1≡b≡1(mod2)，可得1≡b2≡3(3a2+1)2+2a4≡3(mod8)，矛盾。

当d=87时，从(2)可知

从(9)可得

将(11)代入(10)可得

设l=(b+36c2+1，b－36c2－1)。因为从上文可知36c2+1和b都是奇数，所以2|l。如果l/2＞1，则l/2必有素因数p。由于l|2b且l|2(36c2+1)，故从(11)可知p是适合p|b，p|36c2+1以及l|96c4的奇素数。但由gcd(36c2+1，c4)=1，gcd(36c2+ 1，2)=1及gcd(36c2+1，3)=1可得gcd(36c2+1，96c4)=1，矛盾。由此可知l=2。由于96=25·3，故从(12)可得

以下按(14)给出的4种情况进行讨论。

当t=2时，从(13)可知

当t=6时，从(13)可知

当t=16时，从(13)可知

从(17)式可得

由(18)和mod29得3(f2－6g2)2≡1(mod29)，但这与矛盾。

当t=48时，从(13)可知

从(19)中第二个等式可得

由引理1知上式无解。证完。

［1］Silverman JH.The Arithmetic of Elliptic Curves［M］.New York:Springer Verlag，1999.

［2］Zhu H L，Chen JH.A note on two diophantine equation y2=nx(x2+1)［J］.Acta Mathematica Sinica，Chinese Series，2007，50(5):1071－1074.

［3］Zigier D.Large intergral point on elliptic curves［J］.Math. comp.，1987，48(177):425－536.

［4］Zhu H L，Chen JH.Intergral point on y2=x3+27x－62［J］.Math.Study，2009，42(2):425－536.

［5］吴华明.椭圆曲线y2=x3+27x－62的整数点［J］.数学学报(中文版)，2010，53(1):205－208.

［6］管训贵.椭圆曲线y2=x3+(p－4)x－2p的整数点［J］.数学进展，2014，43(4):521－526.

［7］Cohn JH E.The diophantine equation y2=Dx4+1(Ⅲ)［J］.Math.Scand，1987，42:180－188.

［责任编辑 毕 伟］

Points on the Elliptic Curve y2=x3－21x－90

LIYa－zhuo1，CUIBao－jun2

(1.Editorial Department of Journal of Shaanxi Xueqian Normal University，Xi'an 710061，China; 2.Department of Mathematics，Gansu Normal University for Nationalites，Hezuo 747000，China)

Using of some known results of quartic Diophantine equation，with elementarymethodswe prove that the elliptic curve y2=x3－21x－90 has only integral points(x，y)=(6，0).

elliptic curve;quartic Diophantine equation;integral point

O156

A

1004－602X(2015)03－0014－02

10.13876/J.cnki.ydnse.2015.03.014

2015 -06 -10

李亚卓(1979—)，女，陕西蒲城人，陕西学前师范学院编辑。