含线性阻尼2D g-Navier-Stokes方程的全局吸引子维数估计
2015-06-07姜金平王小霞
姜金平,王小霞
(延安大学 数学与计算机科学学院,陕西 延安 716000)
含线性阻尼2D g-Navier-Stokes方程的全局吸引子维数估计
姜金平,王小霞
(延安大学 数学与计算机科学学院,陕西 延安 716000)
利用经典的全局吸引子维数估计方法,研究了一类含线性阻尼的非线性自治g-Navier-Stokes系统在无界区域上的全局吸引子的维数估计问题。
g-Navier-Stokes方程;全局吸引子;线性阻尼;维数估计
在流体力学和动力系统中,通常会研究该系统全局吸引子的存在性问题[1-8],在本文中,我们研究无界区域Ω⊂R2上含线性阻尼的g-Navier-Stokes方程的全局吸引子的维数估计问题,含线性阻尼的二维g-Navier-Stokes方程的一般形式如下(见文[1,3]):

在Ω×(0,∞)上。

u(x,t)=0,在∂Ω上。
u(x,0)=u0(x),在Ω上。
这里u(x,t)∈R2,p(x,t)∈R分别表示速度和压力,ν>0且f=f(x)∈(L2(Ω))2,0<m0<g=g(x1,x2)≤M0。这儿g=g(x1,x2)是实值光滑函数。
u和p未知。当g=1时,方程(1)就是通常的二维Naνier-Stokes方程。
1 预备知识
对常数m0和M0,我们假设Poincare不等式在Ω上成立:即存在λ1>0使得

设L2(g)=(L2(Ω))2,且其内积分别为:
(u,v)=∫Ωu·vg d x,u,v∈L2(g)和((u,v))=这里u=(u1,u2),v=(v1,v2)∈。分别定义它们的范数为|·|=(·,·)1/2和‖·‖=((·,·))1/2。
于是由(2)可以知道,范数‖·‖等价于H10(Ω)空间的范数,设D(Ω)是Ω上由具有紧支集的C∞函数构成,设D={v∈D(Ω))2:▽·gv=0在Ω},H为D在L2(g)上的闭包,V为D在H10(g)中的闭包。这里H和V分别具有空间L2(g)和H10(g)上的内积和范数。
由(2)可知:

定义g-Laplacian算子如下:

于是可以将(1)改写如下:
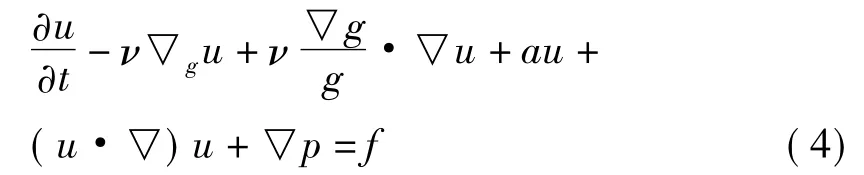
定义g-正交投影为:P:L2(g)→H,同时定义g-Stokes算子为:
(4)式在投影P的作用下,可以得到(1)的弱形式如下:
若f∈V和u0∈H,则

使得

映射bg:Vv×Vg×Vg→R定义为:


这里A:V→V'是g-Stokes算子,其定义为

B(u)=B(u,u)=P(u,▽)u 是双线性算子,其定义为B:V×V→V'

g-Stokes算子A是从空间V到V'的同构,这里B、R满足下面不等式(见文[2-4]):

命题1[1,3]设f∈L2(g),u0(x)∈H,存在一个唯一的u(x,t)∈L∞(R+;H)∩L2(0.T;V)∩C(R+; H)(∀T>0),使得(6),(7)成立。
证明:设u=u(t),t>0是由命题1给定的解。由于u∈L2(0.T;V)及u'∈L2(0.T;V'),则


则bg(u,u,u)=0,∀u,v∈V,于是

从而利用(3)可得
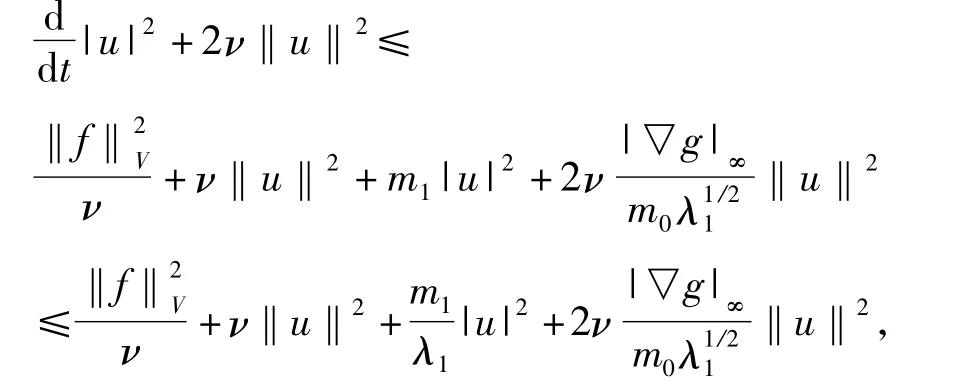
这里m1=|-2α|,因此

对充分小的|▽g|∞,

因此可得:
(一)随着中国经济的不断发展壮大,中国经济对于世界经济的渗透也在不断加深,中国经济已经在国际财经合作中扮演着重要角色。中国与很多国家都建立了各种形式的财经合作体系。2017年的G20峰会是中国第一次作为经济大国参与国际性的重大经济决策,中国对于全球经济恢复起到了推动作用。

由命题1,可以在H上定义连续半群{S(t)}为S(t)u0=u(t),t>0,这里u(t)是(6)的解且u(0)= u0∈H,此外,由(14)有

B在H中对于半群是吸收的。利用文[8]中类似方法可得下面定理成立。
2 全局吸引子的维数估计
给出含线性阻尼的2D g-Navier-Stokes方程在无界区域上的全局吸引子的维数估计。
设u0∈A且u(t)=S(t)u0,对t≥0,由(9)可得线性流u可由下列方程给出

∀Ψ∈H,存在唯一的U∈L2(0.T;V)∩C([0,T];H)(∀T>0)满足(16)∀T>0。
定义线性映射L(t;u0):H→H为L(t;u0)ξ= U(t),可以证明L(t;u0)是有界的且{S(t)}t≥0在A上一致可微,即
这里Qm(τ)=Qm(τ:u0,Ψ1,…,Ψm)是H上的正交投影,L(t;u0)Ψ1,…,L(t;u0)Ψm,∀Ψ1,…,Ψm在H中线性无关。
引理1[7]设A是(1)的全局吸引子,若对n∈N,有qn<0。那么A分别具有有限的Hausdorff和fracta l维数估计如下

为了估计qm,设u0∈A且u(t)=S(t)u0,Uj(t) =L(t;u0)Ψj,t≥0,设φi(t)(i=1…m)是H中的正交基。由于


由Lieb-Thirring不等式


于是
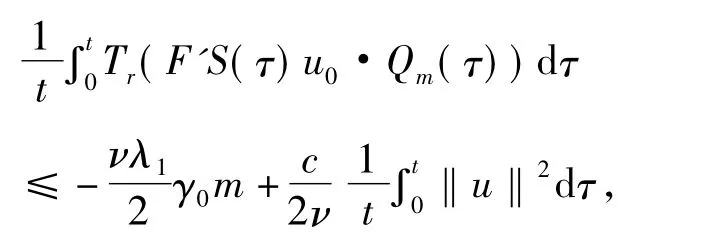


定理3 考虑含线性阻尼的二维g-Navierstokes方程,当时,定义m满足m-这里c是定义在R2上的常数。则其全局吸引子具有有限的Hausdorff维数小于等于m和有限的分形维数小于等于2 m。
[1]Roh J.g-Navier-Stokes equations[D].Minnesota:University of Minnesota,2001.
[2]Hale JK and Raugel G.A damped hyperbolic equation on thin domains[J].Trans.amer.Math.Soc.,1992,329:185-219.
[3]Roh J.Dynamics of the g-Navier-stokes equations[J].J. differential Equations,2005,211:452-484.
[4]Sell G R,You Y.Dynamics of Evolutionary Equations[M]. New York:Applied Mathematical Sciences,2002.
[5]Bae H and Roh J.Existence of solutions of the g-Navier-Stokes equations[J].Taiwanese J.Math,2004,8(1):85-102.
[6]Babin A V.The attractor of a Navier-Stokes system in an unbounded channel-like domain[J].J.Dynam.Differential Equations,1992,4(4):555-584.
[7]Temam R.Infinite-Dimensional Dynamical System in Mechanics and Physics[M].NewYork:Springer-Verlag,1988.
[8]Rosa R.The global attractor for the 2D-Navier-Stokes Flow in some unbounded domain[J].Nonlinear analysis,theory,Methods and Applications,1998,32(1):71-85.
[责任编辑 毕 伟]
Dimension Estimation of G lobal Attractor for g-Navier-Stokes Equation w ith Linear Dampness
JIANG Jin-ping,WANG Xiao-xia
(College of Mathematics and Computer Sctence,Yan'an University,Yan'an,716000,China)
The dimension estimation of global attractor for g-Navier-Stokes equation with linear dampnesswas investigated by the classicalmethod of dimension estimation.
g-Navier-Stokes equation;global attractors;linear dampness;dimension estimation
O175.29
A
1004-602X(2015)03-0010-04
10.13876/J.cnki.ydnse.2015.03.010
2015 -06 -10
陕西省科技计划项目(2014JM2-1005);陕西省教育厅科研项目(15JK1834);延安市科技计划项目(2013-KS03);陕西省2015年大学生创新创业训练项目(1416)
姜金平(1974—),男,陕西洛川人,延安大学副教授,博士。
