基于复杂度的轴流风机动叶偏移时声压信号的表征

李春曦， 林 卿， 叶学民

（华北电力大学 电站设备状态监测与控制教育部重点实验室，河北保定071003）

随着轴流风机的广泛应用，其安全可靠性显得日益重要［1］.在动叶可调轴流风机运行中，因动叶安装角调整异常导致风机出力不足或喘振的现象时有发生，严重影响其运行效率.因此，深入研究动叶异常时轴流风机内的气动噪声和流动状况，对其保持高效低噪安全运行和开发高性能的轴流风机至关重要.

关于轴流风机内流特征和噪声特性的研究一直备受重视.Duquette等［2］探讨了叶片数对小型轴流风机气动性能的影响，表明随着叶片数的增加，在一定范围内风机效率有大幅度提高.Nezym［3］通过对带附加导叶的轴流风机的试验研究，发现对其损失和噪声产生影响的主要因素为附加导叶的高度和出气角度.Fukano等［4］在不同流量系数下对不同叶顶间隙的低压轴流风机进行对比试验，结果表明叶顶间隙泄漏涡相互干扰导致风机噪声增加.方开翔等［5］用叶片穿孔法降低风机噪声，研究发现风机叶片穿孔后噪声降低了3～5dB，且在不同频段上噪声降低幅度不同.此外，一些学者［6－9］还专注于消声、隔声、吸声和隔振等技术研究.

对于动叶安装角异常时的轴流风机，李春曦等［10－12］采用数值模拟方法研究了动叶安装角发生不同程度偏离时风机的内流特征和性能曲线，并通过半经验噪声预测模型得到了该轴流风机气动噪声声功率分布.Posson等［13］仅利用宽频噪声模型分析了动叶偏移时的声功率分布特征.对于叶片异常时声压信号的时域分布特性分析尚未开展.

复杂度反映了一个时间序列与随机序列的接近程度，信号复杂度与信号的有序性和随机行为有关，复杂度被视为信号所代表系统状态的特征参数.复杂度分析是一种信号时域结构的定量分析方法，将简单、复杂等定性、模糊的概念定量化，并给出定量描述指标，所以复杂度可作为一个声压信号复杂程度的量度.目前，复杂度在旋转机械的非线性时间序列研究中已得到广泛发展.朱永生等［14］基于非线性动力系统理论，引入Lempel－Ziv复杂度指标评价滚动轴承运行状态.王炳成等［15］应用近似熵和李亚谱诺夫指数等非线性多参数方法诊断了旋转机械故障，得到了多个非线性特征量.赵鹏等［16］针对离心泵振动信号的非平稳特征，提出一种基于经验模式分解复杂度特征和最小二乘支持向量机的离心泵振动故障诊断方法.

笔者采用大涡模拟LES与基于Lighthill声类比的FW－H 模型相结合的方法，对轴流风机进行数值模拟.该方法考虑了运动物体边界对声源的影响及四极子源、偶极子源和单极子源叠加的相互作用，更具普遍适用性和可行性［17］.通过模拟轴流风机动叶偏移时声压信号的分布特性，分析该轴流风机单动叶安装角偏离度Δβ（以下简称偏离度）在0°～50°内的功率谱密度变化，并通过小波分解，以近似系数ca4的单支重构信号作为分析信号，探讨近似熵、样本熵和Lempel－Ziv复杂度算法的复杂度测度及其表征能力，进一步分析该轴流风机动叶偏移时声压信号的时域分布特征.

1 数值计算

所用风机模型为带有后导叶的OB－84型单级动叶可调轴流风机，动叶数为14，转速为1 200r／min.该风机数据齐全，具备动叶安装角为29°、32°和35°时的特性曲线，为数值计算的可靠性验证提供了依据.模拟表明，不同动叶安装角下该风机的声学特征类似，为此，选择动叶安装角为32°的风机模型进行数值计算.经网格无关性验证，选取总计算单元数约为242万，动、静叶区分别约为104万和49万，此时模拟范围内全压的平均误差为1.2%.

在大涡模拟LES非定常计算中，采用有限容积法离散滤波后的控制方程，压力、速度耦合为PISO解法，动叶轮旋转域采用滑移网格模型，并选用精度较高的二阶隐式时间推进法进行风机气动噪声模拟，其中时间步长Δt＝10－5，完全满足Δt不超过最小网格与当地风速比值的要求［18］.当动叶轮转矩监测曲线与出口总压监测曲线呈周期性平稳波动时，认为该计算过程已达到稳定状态，此时提取声源数据，再引入基于Lighthill声类比的FW－H 模型计算风机各测点声压脉动信号.此模型选择动叶轮旋转域为声源面，噪声监测点分别在集流区、动叶区、导叶区和扩压区沿径向、轴向随机选取.经验证，相同区域内监测点测得的声压特性曲线类似，故每个区域只取一个具有代表性的监测点用于表征不同区域的气动噪声特性（如图1所示）.监测点布置在流道内，这样既能准确获得对应部位的声学参数，又可避免风机外壳（相对于监测点取在壳外）对气动噪声预测的影响；同时，因获得的是近声源数据，可为设计低噪声轴流风机提供参考数据.

图1 监测点位置分布Fig.1 Arrangement of measuring points in the axial flow fan

采用偏离度Δβ 表示动叶安装角的偏离状态，Δβ＝0°时表示动叶安装角处于正常状态（即动叶安装角为32°），不同偏离度代表该叶片沿翼型轴线逆时针旋转偏离正常状态下的角度（见图2）.

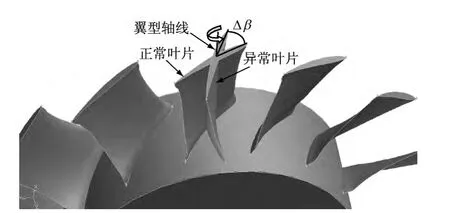
图2 动叶安装角偏离度Fig.2 Deviation degree of blade installation angle

图3 给出了设计流量下，风机在一个旋转周期内的声压时域特性.由图3可知，不同区域的声压时域特性各异，但均呈现出周期性或类周期性特征.动叶安装角异常对声压时域特性的影响主要体现为声压脉动形态、脉动区间和幅值的变化.异常工况下，动叶区声压幅值变化明显，但仍呈周期性脉动；导叶区的声压特征总体呈“V”形分布，并随Δβ 的增大“V”形拐点处向负声压方向发展；集流区和扩压区的声压时域特性类似，随着Δβ的增大，声压脉动幅度加剧，峰值逐渐突出.

监测点的声压信号经快速傅里叶变换，可得到声压频域特性－功率谱密度.图4给出了动叶区功率谱密度分布（取0～1 200Hz频段，此频段包含4倍的基频频程）.由图4可知，该风机的能量集中在0～500Hz内，气动噪声主要表现为低频噪声.另外，该频段的噪声信号具有明显的离散峰值特征，这些低频峰值与涡脱落的频率有关.由于叶轮旋转，叶片周期性地作用于气体，气体压力呈现周期性脉动，导致其在基频处（280Hz）存在一个明显的峰值，且在两倍频、三倍频处也存在较明显的峰值，但其能量都低于基频处的能量.

动叶安装角异常时，功率谱密度离散峰值变化并不明显，在基频和二次谐波处仍表现为明显的峰值特征.但随Δβ的增大，低频段可看到较为强烈的宽频脉动，这是由于动叶安装角异常加剧了动叶区气流无规则扰动，致使压力脉动显著增强.

功率谱密度分析将信号整体经傅里叶变换转换到频域空间，但并不能反映噪声的局部奇异性，因而无法全面表述信号的时域性质，如时间序列的规律性和复杂度.为此，笔者在小波分析基础上，通过提取各区域声压信号的特征熵来进一步分析该风机的噪声特性.

图3 声压时域特性Fig.3 Time－domain sound pressure characteristics

2 小波分析

小波分析不仅继承了傅里叶变换的局部化思想，而且克服了窗口大小不随频率变化、缺乏离散正交基的缺点，具有良好的时频局部化性质.小波分解采用滑动可变的时频窗对信号进行加工，将信号分解到一个由小波伸缩而成的基函数族上，在通频范围内得到分布在不同频段内的分解系列，这样通过分析所需频段的信号变化，并对其进行量化，使得识别风机动叶的工作状态更直观、更容易［19］.

图4 动叶区功率谱密度Fig.4 Power spectrum density in blade region

该风机所测声压信号的最大有效频率为50 000 Hz，采用四尺度小波分解最终可得到频率为3 125 Hz信号频段，以此作为分析频段并进行信号重构.这是因为该风机的噪声能量和故障特征主要集中在低频段，分析3 125 Hz信号频段，可得到噪声频谱局部特征并能准确反映其基本特性.选取小波基时，需要考虑其时、频两域的紧支撑性和带通滤波性能；另外，为了能准确检测出信号中的奇异点，所选择的小波又必须具有正则性（均匀性）.综上所述，选择Daubechies3小波（即db3 小波）进行四尺度小波分解.

以额定流量系数φ＝0.223、Δβ＝40°时扩压区声压信号为例，图5给出了该信号各尺度近似系数及ca4重构信号分布.利用db3小波对其进行4层小波分解.该方法主要对信号s的低频进行细化分解，最终得到的分解频带从低到高分别为：ca4、cd4、cd3、cd2和cd1.对近似系数ca4在低频下进行单支重构得到重构信号a4.

3 复杂度分析

3.1 近似熵

近似熵（Approximate Entropy）算法从衡量信号序列复杂性的角度提供了一种表征信号特征的无量纲指标，具有所需数据量小、对确定性信号和随机信号适用广泛等特点，可看成是高维空间中相矢量的聚集程度.设采集到的原始数据长度为N，近似熵Ea的最终表达式［20］为：Ea（m，r，N）＝Φm（）r－Φm＋1（）r，由此可知，Ea与相似容限r和模式嵌入维数m 的取值有关，据近似熵创始人Pincus 的建议［21］，取m＝2，r＝0.1～0.25 S，S 为原始数据的标准差，本文选取r＝0.2 S.

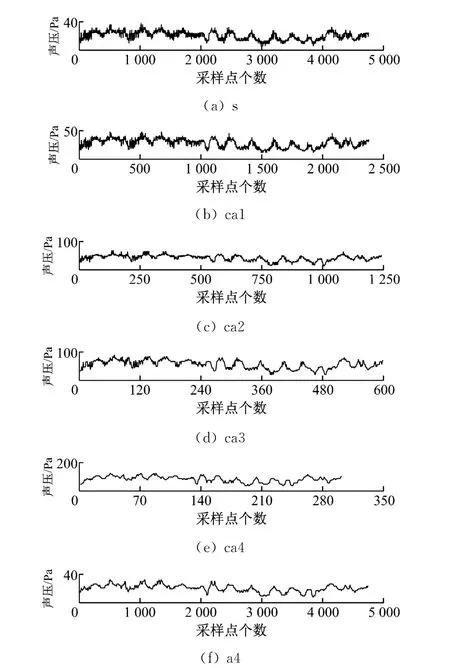
图5 各尺度近似系数及重构信号Fig.5 Approximate coefficients of each scale and distribution of reconstructed signals

图6 给出了风机各区域的近似熵分布.由图6可知，各区域近似熵表现出不同的变化规律，且随着Δβ的增大，在声压幅值增大的情况下，近似熵并未呈现有序的递增趋势.这是因为近似熵反映了信号序列在模式上的自相似程度，只具有相对含义而与时间序列的绝对幅值无关［22］.

从另一个角度讲，当维数变化时在衡量该时间序列产生新模式的概率大小时，产生新模式的概率越大，时间序列越复杂.因此，理论上近似熵能够表征信号的不规则性（复杂性），越复杂的信号，近似熵应该越大.综合比较所有区域各偏离度下近似熵所在数值区间，不难发现其最大值和最小值对应的偏离度为Δβ＝50°和Δβ＝40°，这表明Δβ＝50°时对应的声压信号最为复杂，更偏向于随机信号；而Δβ＝40°时的声压信号相比其他偏离度时较简单，规律性最强.

图6 风机各区域近似熵分布Fig.6 Approximate entropy distribution in each region

在动叶区，Δβ＝50°的近似熵明显高于其他情形，对于大偏转角下的风机异常叶片辨识度较高.集流区和扩压区的近似熵分布规律类似，可根据近似熵数值大小明显区分偏离度，近似熵从小到大依次代表Δβ为40°、30°、0°、20°、10°和50°.此特征可用于快速识别异常动叶安装角的偏离状态.

3.2 样本熵

样本熵实质上是近似熵的优化，其物理意义与近似熵大致相同，样本熵值越大，序列越复杂.二者主要的不同点是：样本熵不包括统计矢量自匹配，因而减小了误差，所以样本熵的区分能力更强［23］.用样本熵来度量风机声压信号的复杂性主要表现为：样本熵值越小，表明风机声压信号序列的自我相似性越高；样本熵值越大，表明风机声压信号的复杂度越高.

序列长度为N 时样本熵的估计值可表示为［24］：对其值起决定性作用的同样是r和m，此处取m＝2，r＝0.2.

图7给出了风机各区域的样本熵分布.由图7可知，各区域样本熵的变化规律与近似熵基本一致，且在集流区和扩压区同样可用样本熵数值大小来识别偏离度，样本熵从小到大依次代表Δβ为40°、30°、0°、20°、10°和50°.另外，在图7（c）和图7（d）中，各偏离度对应曲线间的交集较少，曲线分明，特征更加直观，因此样本熵较近似熵表现出更好的区分能力，这也验证了样本熵受模式嵌入维数m 影响较小而不受数据长度限制的优势.

综上所述，样本熵表现为与近似熵同样的变化规律，但其对偏离度的区分能力更好.且由于距离声源域较远的集流区和扩压区内气动特性相对稳定，测得噪声受干扰程度小，其监测点所得噪声脉动信号表现出更强的规律性.

3.3 Lempel－Ziv复杂度

所研究轴流风机的气动噪声主要为离散噪声掺杂着宽频噪声，这是一种复杂的非平稳随机信号，而由Lempel和Ziv提出的复杂度可反映一个时间序列随序列长度的增加出现新模式的速率，其广泛应用于非 线 性 研 究［25－26］.计 算Lempel－Ziv复 杂 度，首先是对时间序列进行粗粒化处理，再经归一化处理后，Lempel－Ziv复杂度表达式为［27］

式中：n为数据长度；c（n）代表字符串个数.

由此可见，完全随机序列的复杂度趋近于1，规律序列的复杂度趋近于0.

图8给出了风机各区域的Lempel－Ziv复杂度分布.由图8 可知，各区域Lempel－Ziv复杂度均维持在0.25 以下的较低水平，且动叶区Lempel－Ziv复杂度最低，其值在0.16以下，这是因为动叶区声压信号表现为周期性脉动，规律性很强.在距离声源域较远的集流区和扩压区受异常叶片影响不大，故不同偏离度下的Lempel－Ziv复杂度分布较发散，区别度高，尤其在大流量区（φ≥0.25）很容易辨识各偏离度，Lempel－Ziv复杂度由小到大依次对应的Δβ为40°、30°、20°、0°、10°和50°.该结论与近似熵、样本熵所得的结果类似，唯一的区别在于Δβ＝0°和Δβ＝20°的复杂度大小.比较图6～图8不难发现，Δβ＝0°和Δβ＝20°时所对应的复杂度差距很小，因此，可以说Lempel－Ziv复杂度与近似熵和样本熵所得结论基本一致.

图7 风机各区域样本熵分布Fig.7 Sample entropy distribution in each region

图8 风机各区域Lempel－Ziv复杂度分布Fig.8 Lempel－Ziv complexity distribution in each region

4 结 论

（1）动叶安装角偏离后，导叶区、扩压区和集流区的声压脉动形态、脉动区间和幅值均发生改变，而动叶区声压信号仍表现为规律的周期性脉动，只是幅值变化明显.由功率谱密度分布可以看出，该风机气动噪声主要表现为低频噪声，且在低频区的基频和二次谐波处具有明显的峰值特征，但二次谐波处的能量比基频处的低.

（2）由于动叶区声压信号表现为规律的周期性脉动，而单动叶安装角异常时，声压脉动形态并未发生明显变化，所以近似熵、样本熵和Lempel－Ziv复杂度针对动叶区的复杂度测度较小，表明动叶区声压信号分布更加规则.集流区和扩压区距离声源域较远，在这2个区域内3种复杂度算法均具有很强的表征能力，其中样本熵较近似熵区分能力更好，而Lempel－Ziv复杂度与近似熵和样本熵所得结论基本一致.

［1］ SALUNKHE P B，JOSEPH J，PRADEEP A M.Active feedback control of stall in an axial flow fan under dynamic inflow distortion［J］.Experimental Thermal and Fluid Science，2011，35（6）：1135－1142.

［2］ DUQUETTE M M，VISSER K D.Numerical implications of solidity and blade number on rotor performance of horizontal－axis wind turbines［J］.Journal of Solar Energy Engineering，2003，125（4）：425－432.

［3］ NEZYM V Y.Use of turning additional blades in compressor rotor［C］／／ASME Turbo Expo 2005：Power for Land，Sea，and Air.Reno－Tahoe，USA：ASME，2005：85－91.

［4］ FUKANO T，JANG C M.Tip clearance noise of axial flow fans operating at design and off－design condition［J］.Journal of Sound and Vibration，2004，275（3／4／5）：1027－1050.

［5］ 方开翔，李豪杰，高慧.基于Fluent6.0的风机流场模拟与噪声预估［J］.江苏科技大学学报：自然科学版，2008，22（4）：42－47.FANG Kaixiang，LI Haojie，GAO Hui.Simulation of inside flow field and noise forecast for a fan based on Fluent6.0［J］.Journal of Jiangsu University of Science＆Technology：Natural Science Edition，2008，22（4）：42－47.

［6］ DAEHWAN K，CHEOLUNG C，WEUI B J.The use of a hybrid model to compute the nonlinear acoustic performance of silencers for the finite amplitude acoustic wave［J］.Journal of Sound and Vibration，2010，329（11）：2158－2176.

［7］ KELLER J，PARRONDO J，BARRIO R.Effects of the pump－circuit acoustic coupling on the blade－passing frequency perturbations［J］.Applied Acoustics，2014，76：150－156.

［8］ OLIVIER C，VALERIE P B，FRANK S.Panel of resonators with variable resonance frequency for noise control［J］.Applied Acoustics，2012，73（8）：781－790.

［9］ FRANTIŠEK T，FRANTIŠEKŠ，JOZEF B.Complex approach to the vibrodiagnostic analysis of excessive vibration of the exhaust fan［J］.Engineering Failure Analysis，2014，37：86－95.

［10］ 李春曦，尹攀，叶学民.变工况下动叶安装角异常对轴流风机气动和噪声特性的影响［J］.动力工程学报，2013，33（7）：530－538.LI Chunxi，YIN Pan，YE Xuemin.Influence of abnormal blade installation angle on aerodynamic and acoustic characteristics of axial flow fan under variable working conditions［J］.Journal of Chinese Society of Power Engineering，2013，33（7）：530－538.

［11］ 李春曦，尹攀，叶学民.单动叶安装角深度异常对轴流风机性能及噪声影响的数值模拟［J］.中国电机工程学报，2012，32（35）：122－128.LI Chunxi，YIN Pan，YE Xuemin.Simulation on performance and acoustic characteristics with deeply abnormal installation angle of single blade in a variable pitch axial fan［J］.Proceedings of the CSEE，2012，32（35）：122－128.

［12］ 叶学民，李春曦，尹攀.动叶安装角异常反向偏离对轴流风机性能的影响［J］.动力工程学报，2013，33（9）：450－458.YE Xuemin，LI Chunxi，YIN Pan.Effect of abnormal blade reverse deviation on performance of the axial fan［J］.Journal of Chinese Society of Power Engineering，2013，33（9）：450－458.

［13］ POSSON H，MOREAU S，ROGER M.Broadband noise prediction of fan outlet guide vane using a cascade response function［J］.Journal of Sound and Vibration，2011，330（25）：6153－6183.

［14］ 朱永生，袁幸，张优云，等.滚动轴承复合故障振动建模及Lempel－Ziv复杂度评价［J］.振动与冲击，2013，32（16）：23－29.ZHU Yongsheng，YUAN Xing，ZHANG Youyun，et al.Vibration modeling of rolling bearings considering compound multi－defect and appraisal with Lempel－Ziv complexity［J］.Journal of Vibration and Shock，2013，32（16）：23－29.

［15］ 王炳成，任朝晖，闻邦椿.基于非线性多参数的旋转机械故障诊断方法［J］.机械工程学报，2012，48（5）：63－69.WANG Bingcheng，REN Zhaohui，WEN Bangchun.Fault diagnoses method of rotating machines based on nonlinear multi－parameters［J］.Journal of Mechanical Engineering，2012，48（5）：63－69.

［16］ 赵鹏，周云龙，孙斌.基于经验模式分解复杂度特征和最小二乘支持向量机的离心泵振动故障诊断［J］.中国电机工程学报，2009，29（增刊）：138－144.ZHAO Peng，ZHOU Yunlong，SUN Bin.Vibration fault diagnosis of centrifugal pump based on empirical mode decomposition complexity feature and least square support vector machine［J］.Proceedings of the CSEE，2009，29（sup）：138－144.

［17］ 房菲.对旋风机气动噪声特性和预测方法研究［D］.青岛：山东科技大学，2011.

［18］ 李业，周水清，王军，等.转速对弯掠轴流风机气动噪声的影响分析［J］.工程热物理学报，2014，35（1）：51－55.LI Ye，ZHOU Shuiqing，WANG Jun，et al.Analysis of aerodynamic noise of a swept－curved axial flow fan with different rotate speed［J］.Journal of Engineering Thermophysics，2014，35（1）：51－55.

［19］ 张斌，王彤，谷传纲，等.基于动态压力数据的湍流采样数据量分析［J］.工程热物理学报，2010，31（2）：292－294.ZHANG Bin，WANG Tong，GU Chuangang，et al.Research on the data size in turbulent sampling based on dynamic pressure data［J］.Journal of Engineering Thermophysics，2010，31（2）：292－294.

［20］ WANG X W，NIE D，LU B L.Emotional state classification from EEG data using machine learning approach［J］.Neurocomputing，2014，129：94－106.

［21］ LIU Jianping，ZHANG Chong，ZHENG Chongxun.EEG－based estimation of mental fatigue by using KPCA－HMM and complexity parameters［J］.Biomedical Signal Processing and Control，2010，5（2）：124－130.

［22］ 黄娟，黄纯，江亚群，等.基于小波包近似熵的线路故障性质辨识方法［J］.仪器仪表学报，2012，33（9）：2009－2015.HUANG Juan，HUANG Chun，JIANG Yaqun，et al.Identification method of fault characteristics in transmission lines based on wavelet packet and approximate entropy［J］.Chinese Journal of Scientific Instrument，2012，33（9）：2009－2015.

［23］ 赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法［J］.振动与冲击，2012，31（6）：136－154.ZHAO Zhihong，YANG Shaopu.Sample entropybased roller bearing fault diagnosis method［J］.Journal of Vibration and Shock，2012，31（6）：136－154.

［24］ ZUREK S，GUZIK P，PAWLAK S，et al.On the relation between correlation dimension，approximate entropy and sample entropy parameters，and a fast algorithm for their calculation［J］.Statistical Mechanics and Its Applications，2012，391（24）：6601－6610.

［25］ SARLABOUS L，TORRES A，FIZ J A，et al.Index for estimation of muscle force from mechanomyography based on the Lempel－Ziv algorithm［J］.Journal of Electromyography and Kinesiology，2013，23（3）：548－557.

［26］ WANG Z Y，JIN N D，GAO Z K，et al.Nonlinear dynamical analysis of large diameter vertical upward oilgas－water three－phase flow pattern characteristics［J］.Chemical Engineering Science，2010，65（18）：5226－5236.

［27］ TANG Y F，LIU S L，JIANG R H，et al.Correlation between detrended fluctuation analysis and the Lempel－Ziv complexity in nonlinear time series analysis［J］.Chinese Physics B，2013，22（3）：030504－1－030504－7.