超超临界汽轮机中压转子高温蠕变强度分析

吴 穹， 王炜哲， 张军辉， 胡怡丰， 高清辉

（1.上海交通大学 机械与动力工程学院，动力机械与工程教育部重点实验室，上海200240；2.上海交通大学 燃气轮机研究院，上海200240；3.上海电气电站设备有限公司上海汽轮机厂，上海200240）

提高机组进汽参数是提高火电厂运行经济性的 有效手段之一，而材料的高温蠕变失效问题制约着进汽参数的提高.目前，国内某百万等级超超临界机组中压转子的再热进汽参数已提高到5.2MPa／600℃，因此对材料高温蠕变失效问题的研究变得更加重要.转子作为转动部件，其内部应力是影响蠕变变形的一个重要因素，在长时间运行后转子可能产生蠕变脆性断裂，因此研究转子在稳定运行工况下的高温蠕变强度问题对转子设计具有重要意义.

国内外学者对汽轮机转子高温蠕变强度问题进行了大量的研究.某些学者采用基于断裂时间的Larson－Miller参数法，建立起转子硬度－断裂时间－蠕变寿命损耗之间的关系，据此对高温构件进行寿命评估［1－3］.杨凤［4］基于蠕变断裂时间与应力间的指数关系，采用Miner准则计算了某机组中压转子上数个参考点在累计运行2×105h后的蠕变损伤度.Jing等［5］采用Lemaitre非线性损伤度模型和ADINA 有限元软件计算了某汽轮机转子的蠕变损伤度，并与线性损伤度模型－Miner准则进行对比.在这些研究中，基于蠕变断裂时间的Larson－Miller参数法和Lemaitre非线性损伤度模型的应力项被指定为初始应力，没有考虑因蠕变导致的应力变化因素，同时对于转子在稳定运行中的蠕变危险位置并没有予以说明，无法对后续转子的设计作出指导.

笔者以某超超临界机组中压转子为研究对象，采用Abaqus有限元软件和Norton－Bailey 蠕变本构方程，分析了转子在稳定运行工况下的温度场、应力场和应变场，指出多轴效应对转子蠕变性能的影响，并采用Lemaitre非线性损伤度模型来评估转子的连续蠕变损伤度.

1 计算模型

1.1 有限元模型

以图1所示的结构为研究对象，采用简化的二维轴对称模型，利用二次四边形减缩积分热机耦合单元，其中对叶根槽等关键部位的网格进行了加密.经过网格收敛性验证，最后的网格总数确定为67 596.转子入口为再热蒸汽，其参数为5.2 MPa／600 ℃.在计算中，转子受力为传递扭矩引起的剪应力和自重引起的交变拉压应力，这些力相较于转子旋转产生的离心力均可忽略不计，故不予考虑.

图1 中压转子的网格划分Fig.1 Grid division of the IP rotor

1.2 本构模型、转子材料和边界条件

采用Norton－Bailey蠕变本构方程，即

采用类似于塑性应力应变理论的处理原则进行计算［6］.转子材料为12%Cr钢［7］，其在600 ℃下长期工作时具有良好的热强性和热稳定性.图2给出了该材料在600 ℃下通过单轴蠕变试验得到的蠕变－时间－应力关系.

边界条件如下：在温度场计算中，转子表面与周围蒸汽发生换热，将换热方式分为光轴表面、汽封和叶根槽3种形式，这3种形式的传热系数采用推荐的公式［8－9］计算，其中相关结构参数和各部位表面的蒸汽参数由生产厂家提供.转子自身旋转产生离心力，额定转速为3 000r／min，同时叶片旋转产生离心力，以压力的形式加载到叶根槽承力面.在轴承座部位施加固定支撑边界条件.设定转子稳定运行2×105h.

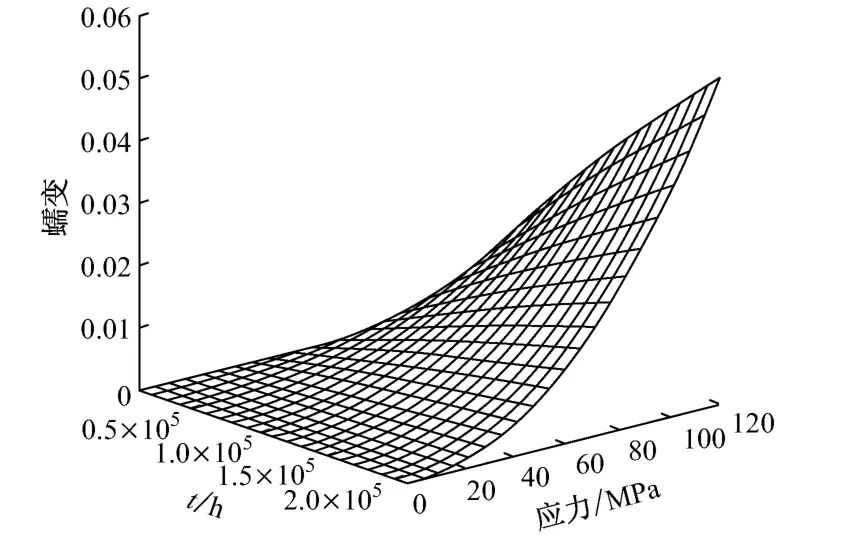
图2 600 ℃下的蠕变－时间－应力关系Fig.2 Creep－time－stress response at 600 ℃

1.3 多轴蠕变设计模型

大多数蠕变考核数据都是在单轴蠕变试验条件下得到的，而汽轮机转子结构和受力特征复杂，蠕变行为呈现多轴特性，必须建立起二者之间的关系.根据文献［10］可知，高温构件失效的实质是材料缺陷形成的微孔洞在经过长大和聚合后发生蠕变断裂.Cocks等提出了受约束孔洞长大理论多轴蠕变设计模型［11］（简称为Cocks－Ashby模型），描述了高温下复杂应力对材料韧性的影响，该模型已在许多国家的高温强度设计标准或评定规范中得到应用，如用于德国大电厂技术协会制定的VGB－R509L 规范［12］.该模型以存在球形缺陷的圆柱体为基本模型，在一系列假设条件下，推导出基于应变的多轴蠕变与单轴蠕变之间的关联式：

式中：FCA为CA 系 数，又 称 为 多 轴 度 因 子；εc，f，uni和εc，f，mul分别为单轴蠕变失效应变和多轴蠕变失效应变；sinh为双曲正弦函数；n 为蠕变试验的Norton指数；σm和σe分别为静水应力和等效应力.

1.4 连续蠕变损伤度模型

考虑到蠕变的多轴性和非线性特性，Lemaitre提出了一种基于热力学的晶间蠕变开裂损伤度演化模型［13－14］：

式中：Rv为反映多轴影响的三轴度因子，与1.3节中提到的多轴度因子都是反映多轴效应的变量，二者都是σm／σe的函数，并且同向变化，即多轴效应越明显，多轴度因子和Rv越大；Dc为连续蠕变损伤度；υ为材料的泊松比；α、λ 和γ 均为与材料有关的常数.

对式（3）进行积分，在t＝0 时刻，Dc＝0，则t0时刻的连续蠕变损伤度为

2 计算结果及分析

2.1 稳态温度场

图3为转子在稳定运行工况下的温度场.对于转子钢，温度高于400 ℃时，蠕变效应必须予以考虑，从图3可以看出，转子大部分区域的温度高于400 ℃，故转子设计中对蠕变的考量是必不可少的.

图3 转子在稳定运行工况下的温度场Fig.3 Temperature distribution during steady－state operation of rotor

2.2 蠕变应变场

图4 为转子在额定工况下稳定运行2×105h后蠕变等效应变百分比（即蠕变等效应变与许用值的比值）的分布.图5 为考虑多轴效应的蠕变等效应变百分比分布.对比图4和图5可知，考虑多轴效应后，叶根槽圆角部位附近及蒸汽入口芯部的蠕变等效应变百分比均发生了较大变化.

2.3 应力场

图4 蠕变等效应变百分比的分布Fig.4 Equivalent creep strain distribution

图5 考虑多轴效应的蠕变等效应变百分比分布Fig.5 Equivalent creep strain distribution considering multiaxial effect

在蠕变变形过程中，晶界孔洞长大导致的局部蠕变率超过附近材料的变形率会引起应力重新分配现象.图6为转子在0时刻和运行2×105h后的应力分布.从图6可以看出，在转子高温区，蠕变变形引起了显著的应力重新分配现象；而在低温区，如转子末几级位置，其应力分布几乎保持不变，0时刻和2×105h时刻的最大Mises应力均为603.2 MPa，其位置位于第13级叶根槽圆角部位.

图6 稳定运行工况下转子在不同时刻的应力分布Fig.6 Mises stress vs.time during steady－state operation

为进一步说明蠕变变形对应力重新分配的影响，选取图7所示的特征点位置来说明应力随时间的变化规律.图7 中的A 点为叶根槽下端圆角部位，B 点靠近叶根槽圆角部位，这2个位置发生了较大的蠕变变形；C 点位于转子蒸汽入口表面，该位置的温度最高；D 点位于转子芯部，该位置发生了较大的蠕变变形.

图8给出了各特征点Mises应力随时间的变化趋 势.A 点、B 点、C 点 和D 点 的Mises应 力 呈 现 出不同的发展趋势：A 点的Mises应力在开始1×104h阶段内从0时刻的162MPa迅速减小至94MPa，在3×104h时刻稳定在91MPa；D 点的Mises应力减小速率略小，从0时刻的80 MPa减小至62 MPa并保持稳定；B 点的Mises 应力有所增大，从23 MPa变为44 MPa；C 点的Mises应力变化不大.由此可以看出，应力重新分配现象主要发生在蠕变初始阶段.

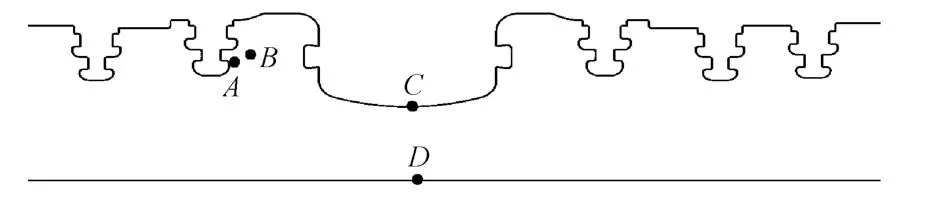
图7 特征点位置Fig.7 Location of characteristic points

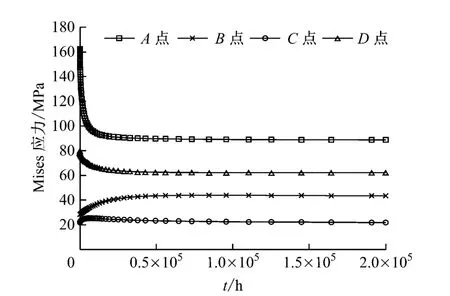
图8 各特征点Mises应力随时间的变化Fig.8 Mises stress vs.time at various characteristic points

2.4 连续蠕变损伤度

图9 给出了各特征点连续蠕变损伤度Dc随时间的变化，其中每条曲线是每个特征点的连续蠕变损伤度Dc与最终蠕变损伤度Dmax的比值.

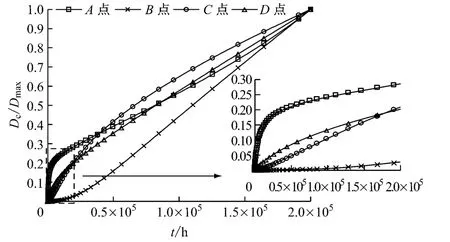
图9 连续蠕变损伤度随时间变化的归一化曲线Fig.9 Normalized continuous damage－time curve

图9 与文献［5］中特征点损伤度分布规律不同的是，损伤度并没有在初期缓慢增大、后期快速增大，相反的是，有些特征点（如A 点、C 点和D 点）的损伤度累积速率在初期较大，到中期时逐渐减小至恒定值，而在后期有所增大；B 点的损伤度累积速率则是从一开始逐渐增大，但变化不大，而且很快达到稳定.由式（3）可知，某一时刻损伤度累积速率主要由当前损伤度、应力和多轴度因子决定.随着时间推移，损伤度累积增加，损伤度累积速率有增大的趋势；应力减小，损伤度累积速率减小；多轴效应增强，损伤度累积速率增大.对于A 点，初期累积损伤度较小，因此应力和Rv主导损伤度累积速率的变化.由图8可知，初期A 点应力显著减小，而该点多轴效应几乎不变，因此损伤度累积速率会减小；在后期，应力和Rv稳定，损伤度较大，损伤度大小主导损伤度累积速率的变化，随着损伤度的增大，损伤度累积速率亦增大.对于B 点，初期应力迅速增大，损伤度累积速率增大；在中后期，应力和Rv逐渐稳定，而且A 点的损伤度较小，导致损伤度变化的非线性并不显著.若不考虑应力重新分配因素，通过连续蠕变损伤度寿命预测模型预测得到的寿命会偏大或者偏小.

3 结 论

（1）转子高温区存在明显的多轴效应.考虑多轴效应后，叶根槽圆角部位附近及蒸汽入口芯部的蠕变等效应变较大.

（2）蠕变伴随着应力重新分配现象，叶根槽圆角部位的初始应力较大，在短时间内应力由162 MPa减小至94 MPa，并稳定下来.部分位置的应力有所增大.

（3）特征点连续蠕变损伤度演化路径受应力重新分配因素的影响，采用连续蠕变损伤度寿命预测模型时必须对应力重新分配因素予以考虑.

［1］ 戴喜庆.大型汽轮机转子寿命损耗和预测研究［D］.北京：华北电力大学，2007.

［2］ 阳萍华.300 MW 汽轮机转子低周疲劳与高温蠕变的寿命计算与研究［D］.长沙：长沙理工大学，2011.

［3］ 胥建群，周克毅，陈锦涛.基于材料老化和蠕变疲劳交互作用汽轮机转子寿命预测［J］.汽轮机技术，2003，45（6）：405－407.XU Jianqun，ZHOU Keyi，CHEN Jintao.Life prediction of steam turbine rotor based on material aging＆creep－fatigue interaction［J］.Turbine Technology，2003，45（6）：405－407.

［4］ 杨凤.汽轮机转子的热应力分析和疲劳寿命研究［D］.沈阳：沈阳工业大学，2007.

［5］ JING Jianping，MENG Guang.A continuum damage mechanics model on creep rupture life assessment of a steam turbine rotor［J］.Journal of Engineering for Gas Turbines and Power，2006，128（1）：173－177.

［6］ 穆霞英.蠕变力学［M］.西安：西安交通大学出版社，1990：46.

［7］ CUI H，SUN F，CHEN K，et al.Precipitation behavior of laves phase in 10% Cr steel X12CrMoWVNbN10－1－1during short－term creep exposure［J］.Materials Science and Engineering：A，2010，527（29）：7505－7509.

［8］ 史进渊，杨宇，邓志成，等.超临界和超超临界汽轮机汽缸传热系数的研究［J］.动力工程，2006，26（1）：1－5.SHI Jinyuan，YANG Yu，DENG Zhicheng，et al.Casing＇s heat transfer coefficients of supercritical and ultra－supercritical steam turbines［J］.Journal of Power Engineering，2006，26（1）：1－5.

［9］ 史进渊，杨宇，邓志成，等.超临界和超超临界汽轮机转子叶根槽传热系数的计算［J］.动力工程学报，2010，30（7）：478－484.SHI Jinyuan，YANG Yu，DENG Zhicheng，et al.Calculation of heat transfer coefficients of blade grooves for supercritical and ultra－supercritical steam turbine rotors［J］.Journal of Chinese Society of Power Engineering，2010，30（7）：478－484.

［10］ GOODALL I W，SKELTON R P.The importance of multiaxial stress in creep deformation and rupture［J］.Fatigue and Fracture of Engineering Material and Structure，2004，27（4）：267－272.

［11］ COCKS A C F，ASHBY M F.Inter－granular fracture during power law creep under multiaxial stress［J］.Material Science Journal，1980（14）：395－402.

［12］ 姚华堂，轩福贞，王正东，等.基于孔洞长大理论的多轴蠕变设计模型及其工程应用［J］.核动力工程，2007，28（3）：72－77.YAO Huatang，XUAN Fuzhen，WANG Zhengdong，et al.Multiaxial creep design models based on the cavity growth theory and its applications in engineering［J］.Nuclear Power Engineering，2007，28（3）：72－77.

［13］ LEMAITRE J，PLUMTREE A.Application of damage concepts to predict creep－fatigue failures［J］.Journal of Engineering Materials and Technology，1979，101（3）：284－292.

［14］ LEMAITRE J.A continuous damage mechanics model for ductile fracture［J］.Journal of Engineering Materials and Technology，1985，107（1）：83－89.