声学CT 算法重建炉内三维温度场的仿真研究

安连锁， 王 然， 沈国清， 张世平

（华北电力大学 国家火力发电工程技术研究中心，北京102206）

大型电站锅炉炉内温度场的测量对于研究炉内燃烧过程具有重要意义，温度场的瞬态变化直接反映了炉内燃烧的变化.由于电站燃煤锅炉尺寸大、工作环境恶劣、炉内燃烧火焰温度高，传统的接触式测温法和一些需要使用精密仪器的测温方法很难在现场使用，并且很难得到炉内三维火焰温度场.一些学者［1－4］利用火焰图像监测装置得到的炉膛燃烧辐射能分布图像信息重建三维燃烧温度场.文献［1］和文献［2］中介绍的三维温度场可视化系统在燃煤锅炉电厂有所应用，该系统能够在5s内刷新其给出的三维温度场分布.但是当采用复杂的算法进行计算分析时，重建速度较慢，在电厂实时在线监测中会出现滞后的现象［3－4］.近年来，声学测温的方法得到了广泛的重视与发展［5－6］.目前，国内外对声学测温的研究主要是针对二维温度场，并且取得了一些成果［7－9］，但是关于三维温度场声学测温方法的研究并不多.利用声学测温方法进行三维温度场重建，进一步得到沿炉膛高度方向的温度分布，这对调整燃烧器摆角、分配炉膛辐射换热量和降低炉膛出口烟气温度都有重要的研究意义.

根据声学测温原理，由多条路径上的声波飞渡时间（Time of Flight，TOF）反演炉膛三维温度场，这是一种新的测温技术，是一个根据结果求取原因的逆问题.其原理类似于计算机层析成像技术，但一般医学CT 技术的投影数据很多，甚至达到数十万个，而由于现场安装条件和成本的限制，一般的声学测量数据只有几十个.如何根据少量的声学测量数据，快速准确地重建出三维温度场是其中的关键.笔者利用2种典型的CT 算法进行重建三维温度场的仿真研究，即代数重建法（Algebraic Reconstruction Techniques，ART）和同步迭代重建法（Simultaneous Iterations Reconstruction Techniques，SIRT），从而利用较少的声学测量数据就能得到准确的温度场信息.

1 三维温度场的重建原理

声学测温方法根据声波在介质中的传播速度来间接得到介质的温度，两者的关系［10］如下：

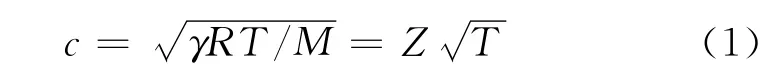
式中：c为声波在介质中的传播速度，m／s；R 为理想气体普适常数，J／（mol·K）；γ 为气体的绝热指数，即比定压热容与比定容热容的比值；T 为气体温度，K；M 为气体摩尔质量，kg／mol.

声学测温原理根据多条路径上的声波飞渡时间来求解三维温度场分布.在得到每条路径上的声波飞渡时间测量数据后，将温度场离散化，建立温度场各个离散网格温度值与TOF 值之间关系的代数方程组，从而把重建温度场的问题转化成求解方程组的问题.

根据声学测温的基本理论，声波在介质中的传播速度函数可以代表温度场函数.基于射线理论的CT 层析成像方法，通过TOF 的走时反演，重建声波传播速度分布，即可重建温度场分布［11］.根据Radon变换公式，令Li为第i 条声波路径，τi为声波飞渡时间，即投影值，则有

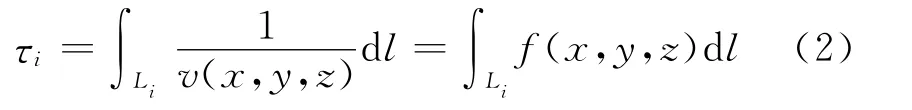
式中：v（x，y，z）为待测区域内声波传播速度；f（x，y，z）为v（x，y，z）的倒数.

假设声学测温系统中有m 条声波路径，将三维的炉膛空间划分为N 个网格，则

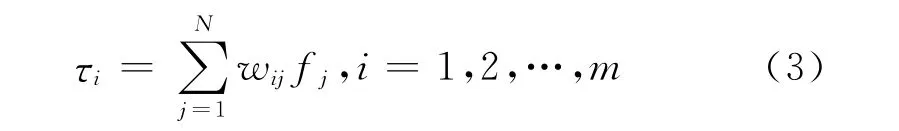
式中：wij为第i条声波路径通过第j 个网格的长度.

经过一个周期的测量，可得到一个线性方程组：

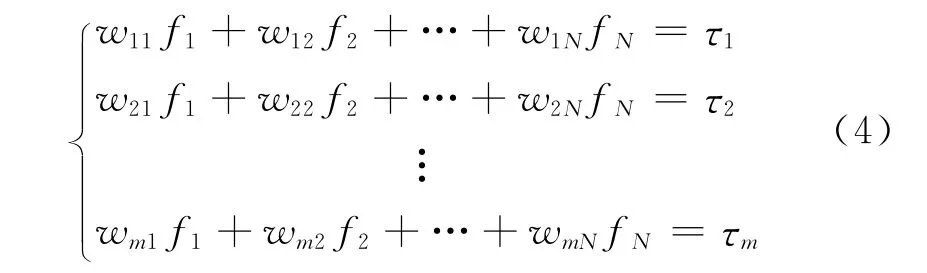
该方程组用矩阵形式可表示为

2 声学CT算法

2.1 ART算法

ART 算法最早被Hounsfield应用在医学CT中，并取得了巨大的成功，后来被发展应用于其他CT 技术中.

ART 算法的基本思想是先假设一初始图像x（0），然后对x（0）采用一定的校正方式求一次近似图像x（1），再根据x（1）求二次近似图像x（2），如此继续，直到满足预定条件为止.根据x（k）求x（k＋1）时加一校正值Δx（k）.Δx（k）只考虑第ik号射线投影的影响，所修正的像素值也限于ik号射线经过的那些像素，下一次迭代时则只考虑第ik＋1号射线.总之，每次校正依次考虑一条射线的射线投影并校正该射线经过的像素，故又称逐线校正.

ART 算法所使用的求解公式［12］如下：

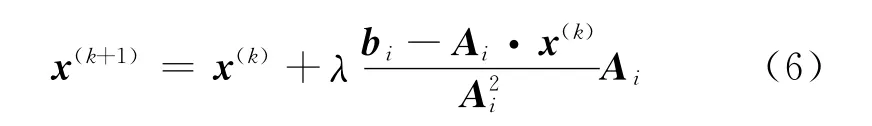
式中：k为迭代次数；λ 为松弛因子；Ai为权因子矩阵A 的第i行；bi为测量数据向量的第i行.

一般情况下，0＜λ＜2.松弛因子的大小是重建结果和重建速度的影响因素之一，通常认为λ 的选择取决于以下因素：最终的重建目的、数据采集的方式、测量的噪声特征和欲重建的迭代次数等.笔者通过试算的方法，发现λ 存在一个最佳取值范围（0.17，0.35）.

2.2 SIRT算法

SIRT 算法是与ART 算法并行的一种CT 迭代重建算法.SIRT 算法旨在使重建图像对测量误差不敏感.

由于ART 算法每次迭代只用到一条射线的射线投影，如果这一射线投影包含误差，那么所得的解也就引入了误差.SIRT 算法在求k＋1 次估计x（k＋1）时，利用k次估计x（k）加上校正图像.校正图像正比于第k次估计的误差矢量的反投影.因而每个像素的校正值实际是通过该像素的所有射线投影误差值累加的，而不是只与一条射线有关，这是与ART 算法的根本区别，也是SIRT 算法能够有效抵制测量数据中噪声的根本原因.由于每一个像素的校正值是所有经过该像素的射线的共同贡献，一些随机误差就被平均掉了.SIRT 算法的校正过程是所有经过某像素的诸多射线的投影误差对该像素值的校正，故又称逐点校正.

所使用的SIRT 算法求解公式［12－13］为

与ART 算法一样，对于重建结果，松弛因子是一个重要的影响因素.笔者通过试算的方法，得到λ的最佳取值范围为（0.30，0.40）.

3 仿真实例

对于目前国内主力机组，锅炉高度一般在10m以上.假设本文中锅炉炉膛高10m，截面为10m×10m 的正方形，这样就形成了一个10m×10m×10m 的待测空间区域.

按照图1所示的方式布置20个声学传感器，考虑到同侧墙壁上的声学传感器之间不会产生明显有效的信号，除去其自身和同侧墙壁上的声学传感器，共可形成58条独立有效的声波路径.将待测空间区域均匀地分割成3×3×3＝27个空间网格，每条声波路径上的TOF由模型温度场在该路径上的积分得到.

图1 声学测温仿真模型示意图Fig.1 Simulation model of the acoustic pyrometry

下面对几种典型模型的温度场分别进行重建.选取了3种典型模型的温度场：单峰模型温度场、双峰模型温度场和四峰模型温度场.

其中，单峰模型温度场函数为

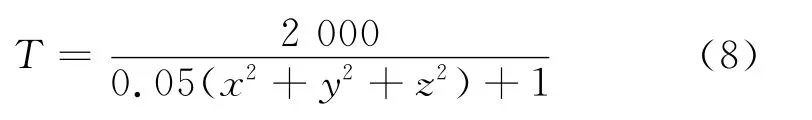
双峰模型温度场函数为

四峰模型温度场函数为

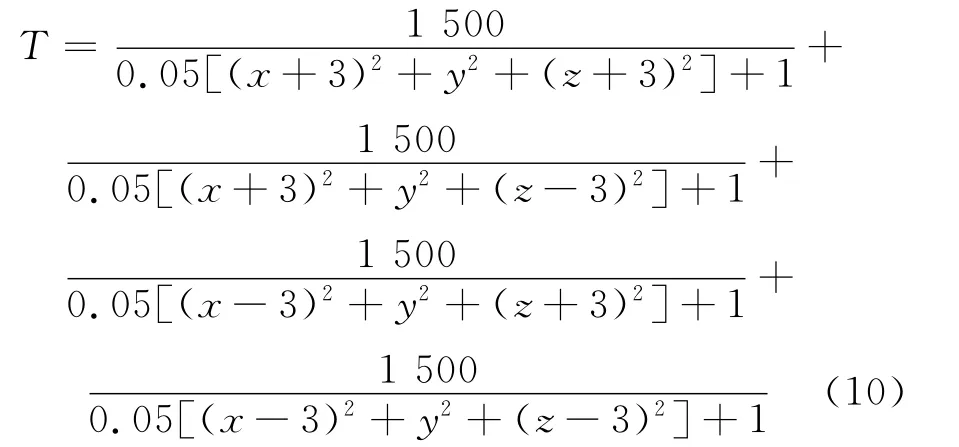
利用CT 算法得到27个空间网格的温度值后，将其作为每个空间网格中心的温度值，再使用距离平方反比法与三次样条插值相结合的方法进行插值，得到重建温度场的切片图（见图2）.由图2 可知，使用2种不同算法得到的温度场均准确地描绘出了模型温度场单峰、双峰和四峰的特征.

将待测空间区域均匀地分割成4×4×3＝48个空间网格再次计算，发现增加空间网格数后，问题的不适定性增大，无法得出有效解.因此，为了增加原始温度点数量，需要对测点布置的位置进行优化，这里暂不讨论.

重建温度场的质量采用平均误差、最大值误差和均方根误差评价，其中最大值误差定义为

图2 模型温度场和重建温度场示意图Fig.2 Temperature field models and the reconstructed temperature field

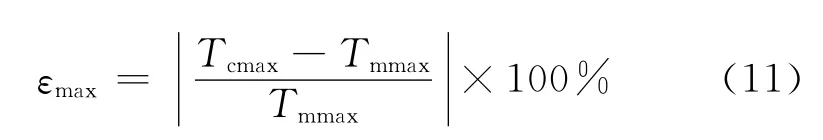
式中：Tmmax为模型温度场的温度最大值；Tcmax为重建温度场的温度最大值.

均方根误差定义为

温度场重建的结果见表1.为了研究TOF测量误差对温度场重建的影响，在计算获得的准确飞行时间值上加上均值为0、标准差为δ的高斯噪声.将δ从0.01逐渐增大至0.05，得到图3～图5所示的趋势图.

由以上温度场重建结果可知：对于简单的单峰模型，2种算法均能得到理想的重建效果，而对于更复杂的双峰模型和四峰模型，重建温度场误差显著增大；在无噪声环境下，2种算法重建效果的差别不大；在有噪声环境下，SIRT 算法具有一定的鲁棒性，而ART 算法对噪声较为敏感，随着测量误差的增大，采用ART 算法重建温度场的误差明显增大.

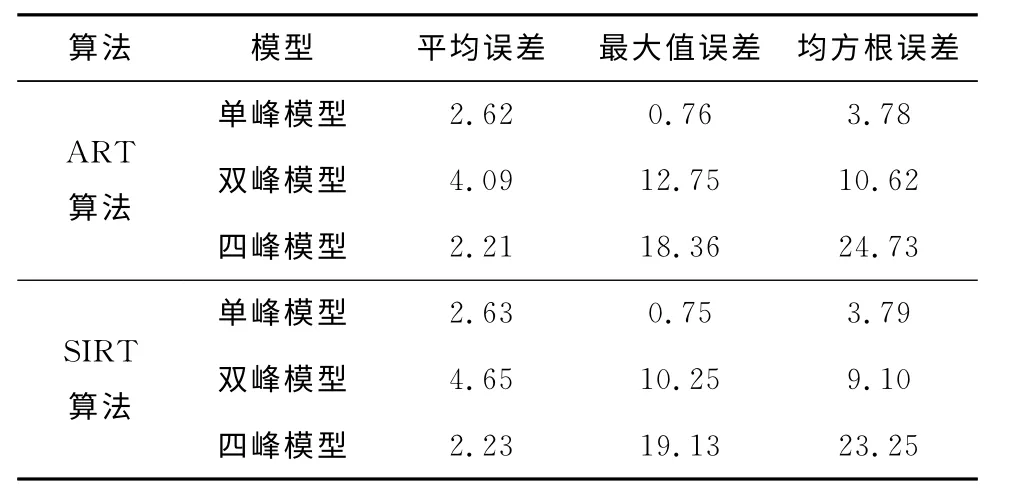
表1 温度场重建结果Tab.1 Results of the reconstructed temperature field %

图3 标准差对单峰模型重建温度场误差的影响Fig.3 Influence of standard deviation on the temperature field reconstruction with single－peak model

图4 标准差对双峰模型重建温度场误差的影响Fig.4 Influence of standard deviation on the temperature field reconstruction with double－peak model

图5 标准差对四峰模型重建温度场误差的影响Fig.5 Influence of standard deviation on the temperature field reconstruction with four－peak model

在重建过程中，SIRT 算法迭代一次相当于ART 算法迭代I次，故ART 算法的重建速度总是比SIRT 算法快.根据CT 基本理 论［14－15］，在测量 数据完全、噪声较小的环境下，SIRT 算法重建质量并不优于ART 算法；但是在测量数据缺失、噪声较大和射线呈弯曲形式的情况下，SIRT 算法具有明显的优越性.在本文的仿真实验中，随着噪声的增大，SIRT 算法显示出比ART 算法更好的鲁棒性也验证了这一点.因此，当声学测点较多、测量数据较完全、噪声较小时，ART 算法具有更快的重建速度和更好的重建质量；而当只有少量声学测量数据、噪声较大时，使用SIRT 算法为宜.

4 结 论

（1）ART 算法和SIRT 算法对于几种典型的三维温度场模型具有较好的重建结果，可以实现炉内三维温度场的声学CT 重建，准确地提供了炉内温度场信息.

（2）ART 算法的重建速度快，但对噪声敏感，并且在测量数据较少的情况下重建质量较差；SIRT算法虽然重建速度慢，但当噪声较大、测量数据不完全或不准确时仍能保持良好的重建精度，在实际应用中SIRT 算法具有更好的稳定性.

［1］ 周怀春，罗自学，娄春.辐射能信号作为锅炉燃烧及机组运行重要监控参数的分析［J］.动力工程学报，2010，30（8）：593－600.ZHOU Huaichun，LUO Zixue，LOU Chun.Significance of taking radiative energy signals as monitoring parameters for boiler combustion adjustment and operation control［J］.Journal of Chinese Society of Power Engineering，2010，30（8）：593－600.

［2］ 周怀春，韩曙东，盛锋，等.炉膛燃烧温度场三维可视化监测方法模拟研究［J］.动力工程，2003，23（1）：2154－2159.ZHOU Huaichun，HAN Shudong，SHENG Feng，et al.Numerical simulation on a visualization monitoring method of three－dimensional temperature distribution in furnace［J］.Power Engineering，2003，23（1）：2154－2159.

［3］ 刘冬，王飞，黄群星，等.三维炉膛温度场重建中病态矩阵方程的求解研究［J］.中国电机工程学报，2007，27（26）：72－77.LIU Dong，WANG Fei，HUANG Qunxing，et al.Study on solving ill－posed matrix equation in reconstruction of three－dimensional temperature distribution in furnace［J］.Proceedings of the CSEE，2007，27（26）：72－77.

［4］ 黄群星，刘冬，王飞，等.基于截断奇异值分解的三维火焰温度场重建研究［J］.物理学报，2007，56（11）：6742－6748.HUANG Qunxing，LIU Dong，WANG Fei，et al.Study on three－dimensional flame temperature distribution reconstruction based on truncated singular value decomposition［J］.Acta Physica Sinica，2007，56（11）：6742－6748.

［5］ 安连锁，李庚生，沈国清，等.声学测温系统在200 MW 电站锅炉中的应用研究［J］.动力工程学报，2011，31（12）：928－932.AN Liansuo，LI Gengsheng，SHEN Guoqing，et al.Application of acoustic pyrometer in a 200MW power plant boiler［J］.Journal of Chinese Society of Power Engineering，2011，31（12）：928－932.

［6］ OSTASHEV V E，VECHERIN S N，WILSON D K，et al.Recent progress in acoustic tomography of the atmosphere［C］／／14th International Symposium for the Advancement of Boundary Layer Remote Sensing.Copenhagen，Denmark：IOP Publishing，2008，012008.

［7］ 颜华，王善辉，周英钢.正则化参数自适应选取的声学CT 温 度 场 重 建［J］.仪 器 仪 表 学 报，2012，33（6）：1301－1307.YAN Hua，WANG Shanhui，ZHOU Yinggang.Acoustic CT temperature field reconstruction based on adaptive regularization parameter selection［J］.Chinese Journal of Scientific Instrument，2012，33（6）：1301－1307.

［8］ 谢李兵，刘彤，张志刚，等.基于迭代和插值算法的二维温度场重建［J］.中国电机工程学报，2004，24（10）：249－252.XIE Libing，LIU Tong，ZHANG Zhigang，et al.The 2－D temperature reconstruction based on the algorithm of interpolation and iterative［J］.Proceedings of the CSEE，2004，24（10）：249－252.

［9］ 沈国清，吴智泉，安连锁，等.基于少量声学数据的炉内温度场重建［J］.动力工程，2007，27（5）：702－706.SHEN Guoqing，WU Zhiquan，AN Liansuo，et al.Reconstruction of temperature fields of furnace on the basis of few acoustic data［J］.Journal of Power Engineering，2007，27（5）：702－706.

［10］ 杜功焕，朱哲民，龚秀芬.声学基础［M］.南京：南京大学出版社，2001.

［11］ 阎生存，李珍照，薛桂玉，等.大坝CT 中ART 算法及其改进探讨［J］.武汉大学学报（工学版），2001，34（4）：29－34.YAN Shengcun，LI Zhenzhao，XUE Guiyu，et al.Discussion on algebraic reconstruction techniques in computerized tomography of dams and its improvement［J］.Engineering Journal of Wuhan University，2001，34（4）：29－34.

［12］ BENDER M，DICK G，GE M，et al.Development of a GNSS water vapour tomography system using algebraic reconstruction techniques［J］.Advances in Space Research，2011，47（10）：1704－1720.

［13］ BARTH M，RAABE A.Acoustic tomographic imaging of temperature and flow fields in air［J］.Measurement Science and Technology，2011，22（3）：035102.

［14］ 庄天戈.CT 原理与算法［M］.上海：上海交通大学出版社，1992.

［15］ 杨艳，秦克伟，张东，等.一种改进的近地表层析成像SIRT 算法［J］.武汉大学学报（理学版），2009，55（2）：201－205.YANG Yan，QIN Kewei，ZHANG Dong，et al.Improvement of SIRT algorithm in near－surface seismic tomography［J］.Journal of Wuhan University（Natural Science Edition），2009，55（2）：201－205.