基于稳定逆的直流炉机组协调控制系统前馈－反馈控制

李 露， 刘吉臻， 项 丹

（华北电力大学 新能源电力系统国家重点实验室，北京102206）

随着电厂运行水平的提高，大容量、高参数的发 电设备得到快速发展，直流炉因其自身优势被广泛应用.考虑到直流炉机组的非线性和强耦合特性，建立能够正确反映机组特性且复杂度适中的机理模型，将其与非线性控制方法结合起来并设计出品质优良的控制系统是需要进一步研究的问题［1］.

为优化直流炉机组的协调控制系统，首先必须建立直流炉机组的数学模型.从1965年起，国内外许多学者就对直流炉机组的解析模型［2］进行过研究，但所建立的模型大多存在表达繁琐或精度不高的问题，无法应用于直流炉机组协调控制系统控制器的设计［3］.近几年来，闫姝等［3］针对直流炉机组协调控制系统的特点，采用机理建模与实验建模相结合的方法，通过合理简化，建立了直流炉机组的非线性模型.该模型在保证精度的前提下降低了变量个数与模型阶次，有利于协调控制系统控制器的设计.

另一方面，有学者针对Åström 建立的160 MW 燃油汽包锅炉的简化非线性模型应用鲁棒控制［4－5］、反 馈 线 性 化［6－7］、反 步 设 计 法［8］和 增 益 调 度法［9－10］等方法进行控制，均取得了一定的控制效果.此外，为了克服非线性环节对协调控制系统性能的影响，房方等［11］将稳定逆理论引入到汽包锅炉协调控制系统的设计中，针对Åström 建立的模型求取其稳定逆解，并结合H∞反馈控制器构建系统的非线性输出跟踪控制结构，减弱不同通道之间的关联耦合作用，同时使系统具有较好的设定值跟随能力.这些非线性控制策略为直流炉机组协调控制系统的设计提供了很好的思路.

笔者首先在闫姝等［3］建立的直流炉机组非线性模型基础上对该模型做进一步简化.经验证，简化模型正确反映了机组的动态特性，同时保证了一定的精度，降低了复杂度，更适用于协调控制系统的设计.考虑到将上述非线性输出跟踪控制结构应用于汽包锅炉协调控制系统时所具有的突出优势，笔者针对简化模型，应用稳定逆理论与前馈－反馈控制结构，一方面求取模型的稳定逆解，利用逆系统前馈控制具有较好的设定值跟随能力以及对非线性对象的适应性，使机组输出迅速达到设定值附近；另一方面设计具有多个输出变量的反馈控制器，以进一步消除外界干扰造成的输出误差.最后在不同的静态工作点下分别进行状态扰动与设定值扰动的仿真实验，并与基于状态反馈线性化的非线性内模结构［5］的控制效果进行对比，验证基于稳定逆的前馈－反馈结构的控制效果.

1 直流炉机组协调控制系统简化模型

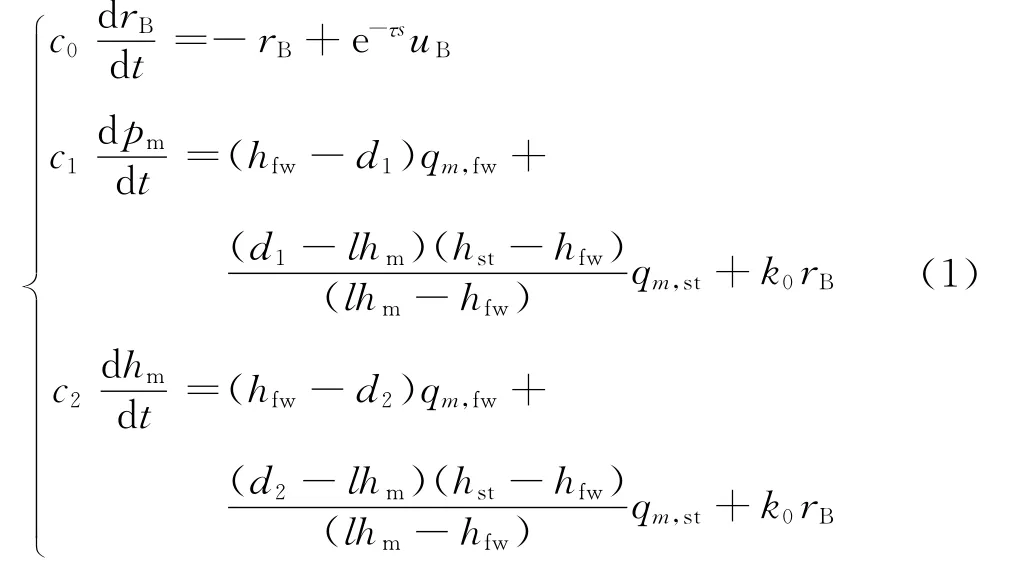
设计直流炉机组协调控制系统的基础是建立具有一定精度且利于控制器设计的直流炉机组数学模型.针对直流炉机组的特点，闫姝［12］提出了如下所示的3阶非线性模型.

其中：

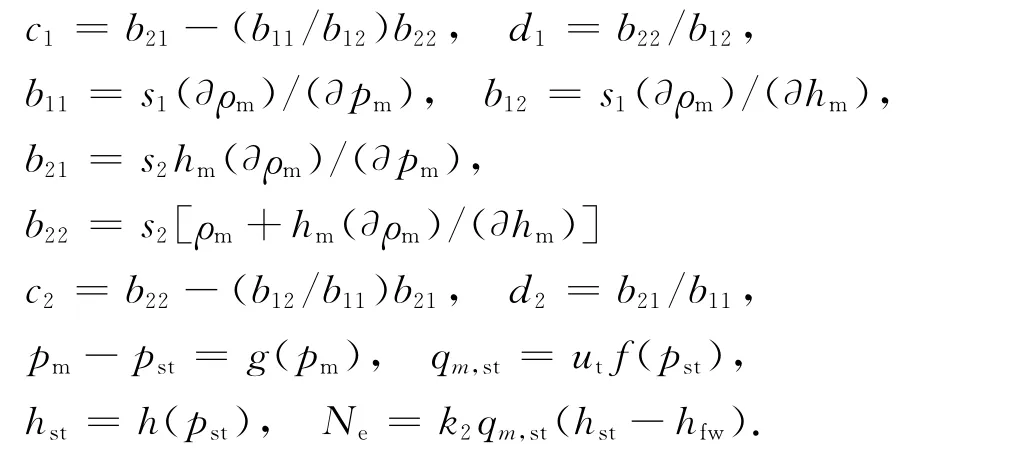
式中：c0为制粉惯性时间，s；rB为进入锅炉煤粉量，kg／s；τ为制粉过程迟延时间，s；uB为燃料量，kg／s；s1为锅炉汽水流程中总质量变化与汽水分离器出口点质量变化的比值；ρm 为汽水分离器出口蒸汽密度，kg／m3；pm为汽水分离器出口蒸汽压力，MPa；s2为锅炉汽水流程中总能量变化与汽水分离器出口点能量变化的比值；hm为汽水分离器出口蒸汽比焓，kJ／kg；hfw为省煤器入口给水比焓，kJ／kg；qm，fw为总给水质量流量，kg／s；l为过热器出口点比焓与分离器出口点比焓的比值；hst为汽轮机入口蒸汽比焓，kJ／kg；k0为燃料有效发热量增益，kJ／kg；pst为汽轮机入口蒸汽压力，MPa；g（·）和f（·）分别代表一种函数关系；qm，st为汽轮机入口蒸汽质量流量，kg／s；ut为汽轮机调节门开度，%；h（·）代表汽轮机入口蒸汽压力与焓值之间的函数关系；Ne为汽轮机功率，MW；k2为汽轮机增益.

闫姝［12］在提出上述机理模型的基础上，结合实验建模的方法，利用某1 000 MW 超超临界机组运行数据求得了模型中的各个参数，并拟合得到g（·）、f（·）和h（·）的具体形式.其中

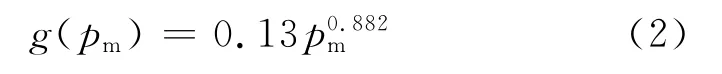
考虑到指数形式的g（·）会造成模型的输出参数pst与输入参数pm之间具有非线性关系，因此采用g（pm）＝0.078pm＋0.249这一线性回归模型代替式（2），以降低直流炉机组的控制难度.

此外，为了更好地应用前文提到的非线性方法设计直流炉机组协调控制系统的控制器，进行以下2点简化：不考虑相对较小的制粉过程的迟延；忽略过热器出口蒸汽喷水减温的环节，即认为hst＝lhm.

基于上述修改得出如下的简化模型：

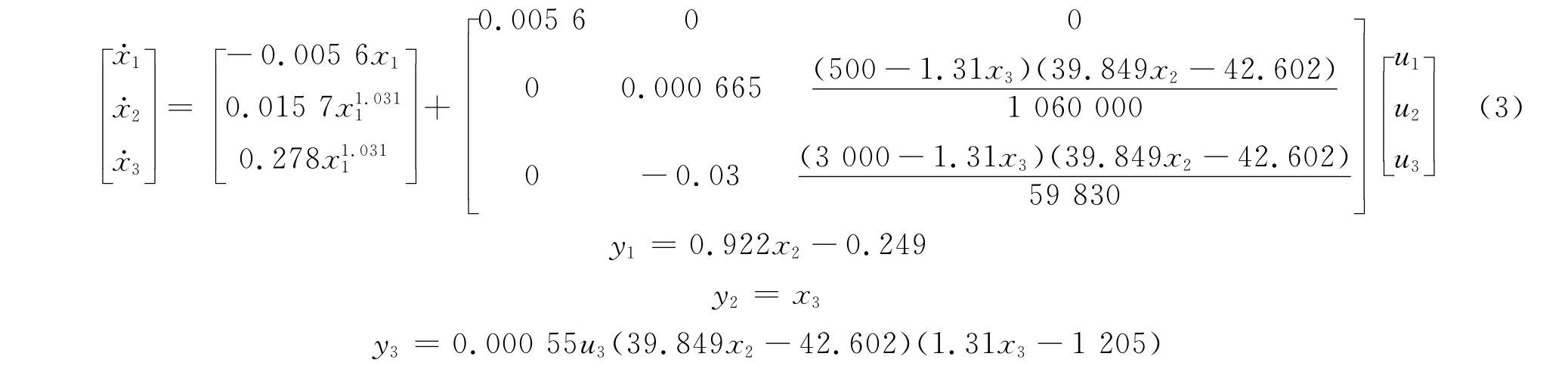
为验证上述简化模型的正确性，首先选取机组的3组静态工作点，对模型进行静态验证.将3组静态工作点数据输入式（3）进行计算，将计算所得到的各个输出值与文献［12］中给出的实际输出数据进行比较，并将所得到的相对误差值以及原模型的计算输出值与实际输出数据间的相对误差列于表1.

表1 简化模型3组静态工作点的验证Tab.1 Verification of the reduced model at three static work points

由表1中数据可以看出，简化模型在3组静态工作点下的输出数据与实测数据之间的相对误差均较小，简化模型具有一定的精度.此外，简化模型的主蒸汽压力pst的相对误差与原模型主蒸汽压力的相对误差完全一致，仅汽轮机功率Ne和汽水分离器出口蒸汽比焓hm的相对误差有所增大，这是由于简化过程引起模型精度下降.

另外，分别将燃料量uB、给水质量流量qm，fw和汽轮机调节门开度ut3个输入量的阶跃信号作为扰动，对简化模型的动态特性进行仿真，其结果与文献［12］中的结果接近，能够反映实际机组的动态特性，进一步证实了简化模型的正确性.

2 基于稳定逆的前馈－反馈控制方法

2.1 基于稳定逆的前馈－反馈控制方法

基于稳定逆的前馈－反馈控制方法的结构见图1［13］.其基本原理为：通过给定期望输出路径Yd，由非线性被控对象的稳定逆系统求出其期望的状态变量与前馈控制输入Ud.一方面，前馈控制可以使系统输出迅速达到设定值附近，并且对非线性对象具有较好的适应性；另一方面，由于实际运行中往往存在各类干扰因素，仅依靠前馈控制不能保证系统输出的稳态无差.因此在前馈控制的基础上结合反馈控制，设计具有多个输出参数的反馈控制器，以进一步消除外界干扰并使系统输出Y 精确跟踪Yd.

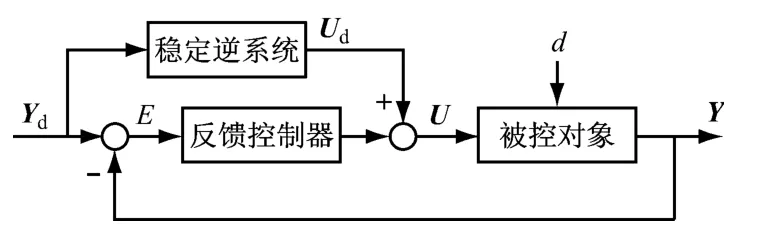
图1 基于稳定逆的前馈－反馈控制结构框图Fig.1 Structure diagram of the feedforward－feedback control based on stable inversion

2.2 非线性系统的稳定逆问题

研究如下形式的多变量仿射非线性系统［11］：

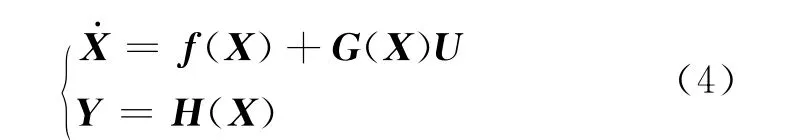
式中：X＝［x1，x2，…，xn］T；U＝［u1，u2，…，um］T；Y＝［y1，y2，…，ym］T；f（X）＝［f1（X），f2（X），…，fm（X）］T；G（X）＝［g1（X），g2（X），…，gm（X）］；H（X）＝［h1（X），h2（X），…，hm（X）］T；fi（X）、gi（X）为充分光滑的向量场，hi（X）为充分光滑的标量函数，其中i＝1，2，…，m.

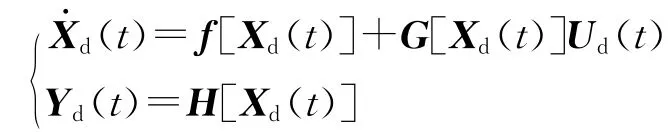
此外，为了求解稳定逆问题，对于平衡点X0领域内的所有X，定义式（4）所描述的非线性系统的相对阶向量［r1，r2，…，rm］为：

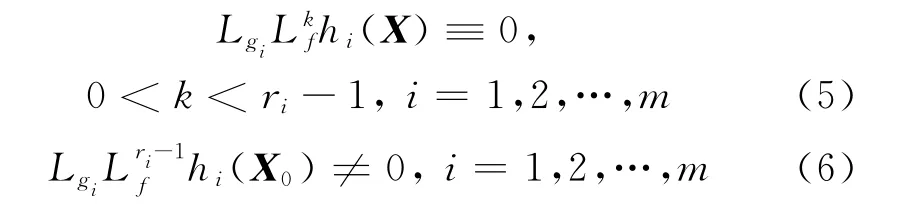
若相对阶向量存在，且满足r1＋r2＋…＋rm＝n，则系统新的输入输出关系［15］可表示为

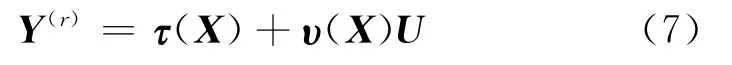
其中，

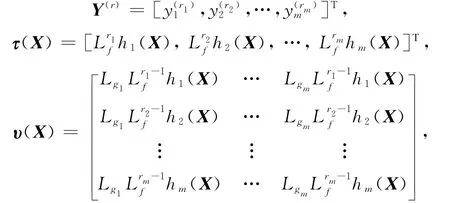
且υ（X）是非奇异的.

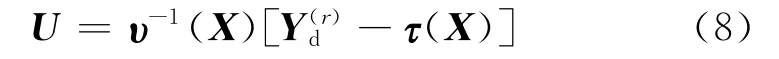
进一步定义

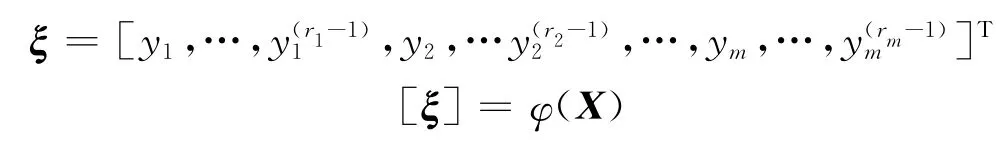
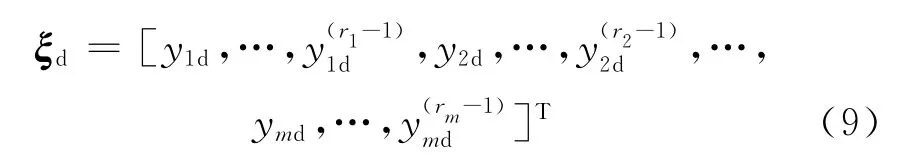
结合式（8）和式（9）即可得到期望输出路径Yd的稳定逆解为

3 直流炉机组协调控制系统的前馈－反馈控制设计

对于直流炉机组协调控制系统的前馈控制设计，必须先求出直流炉机组协调控制系统模型的稳定逆解.假设系统的输出方程为

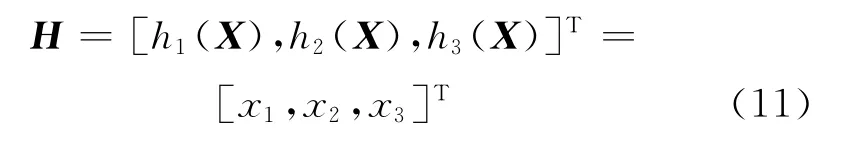
计算系统的相对阶向量［r1，r2，r3］如下：

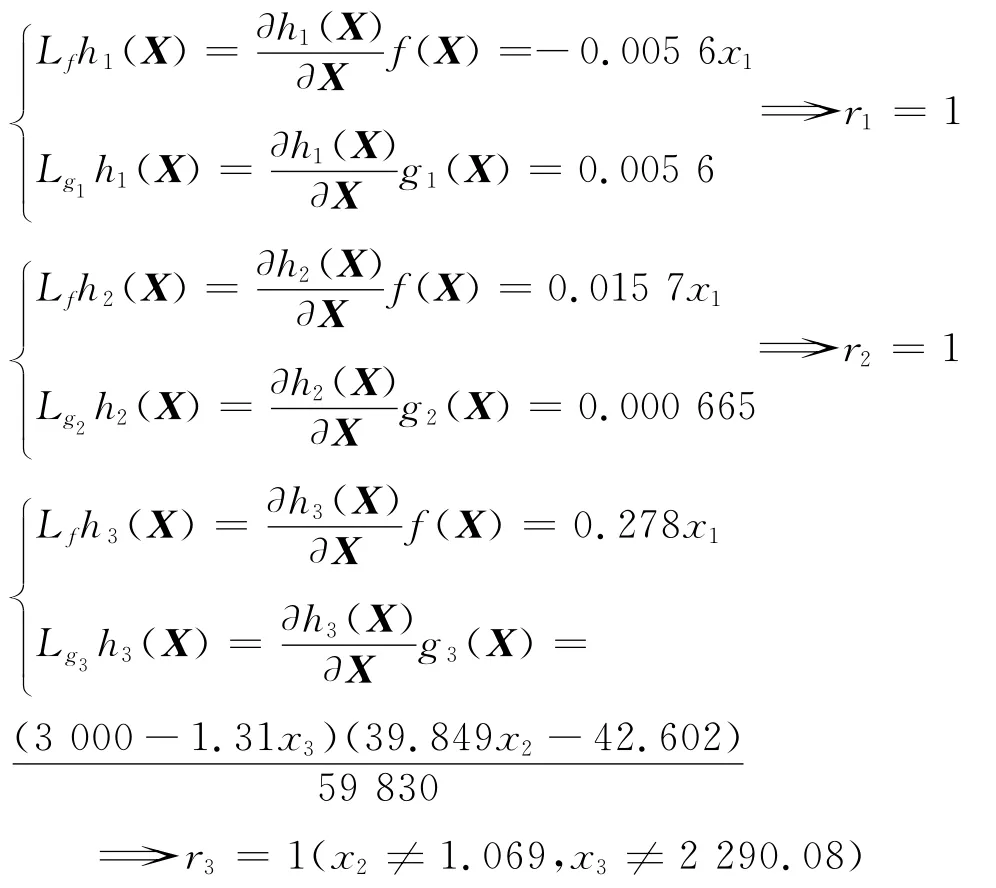
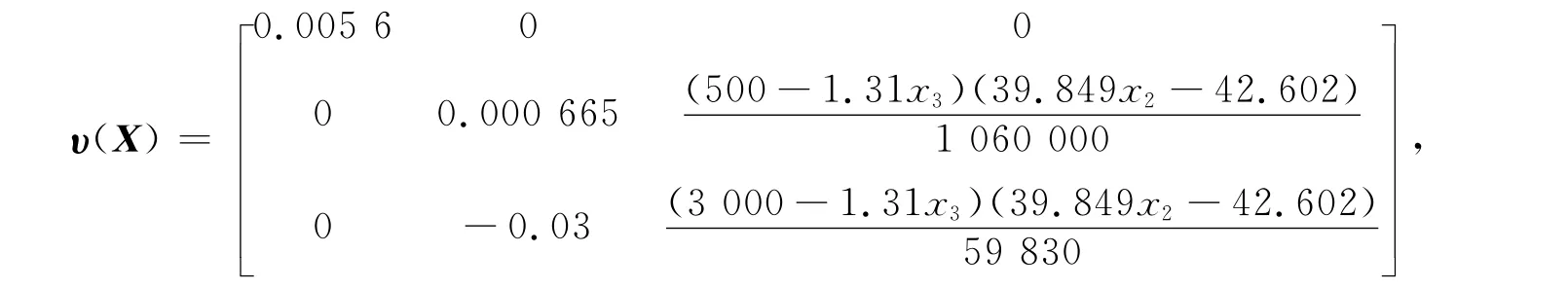
并且上述υ（X）是非奇异的.

此时系统新的输入输出关系为

定义ξ＝［h1，h2，h3］T，X＝φ－1（ξ），则有

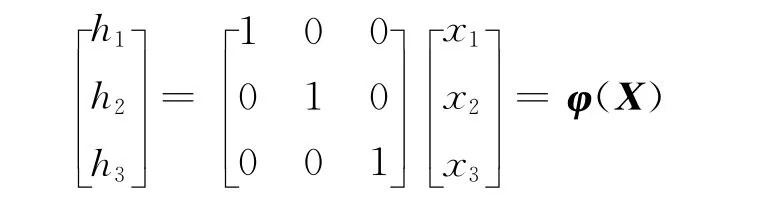
令H＝Xd，由式（10）和式（12）可以得到期望控制输入Ud为

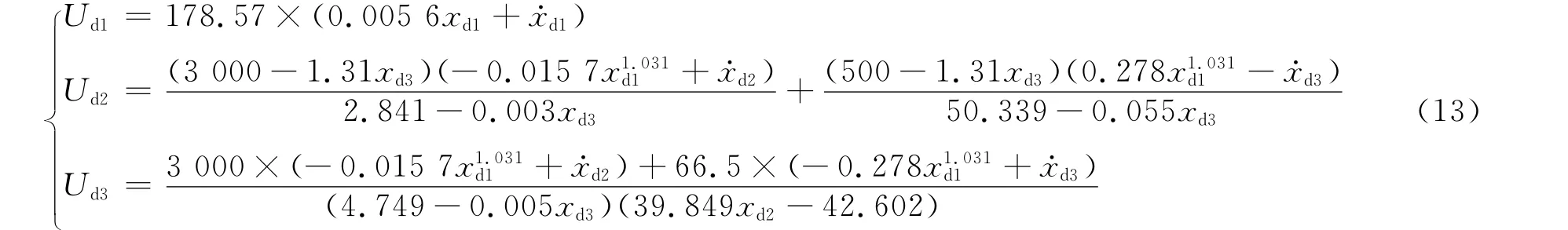
利用以下关系式可由给定的期望输出路径Yd解出期望的状态变量Xd.

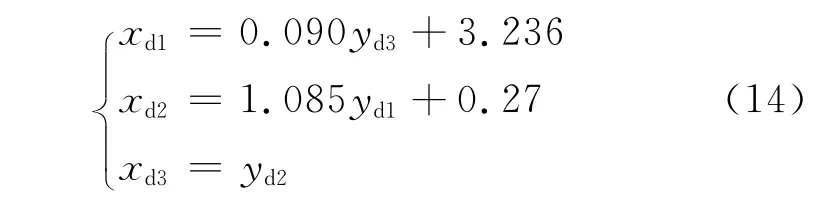
式（14）是对式（3）中模型的输出方程求逆所得的结果.值得说明的是，为了得到xd1与yd3之间的解析关系，笔者采用近似处理的方式：利用表2中给出的4组静态工作点下的机组实测数据，对进入锅炉的煤粉量与输出功率之间的关系进行线性拟合，其结果为：yd3＝11.15xd1－36.08.

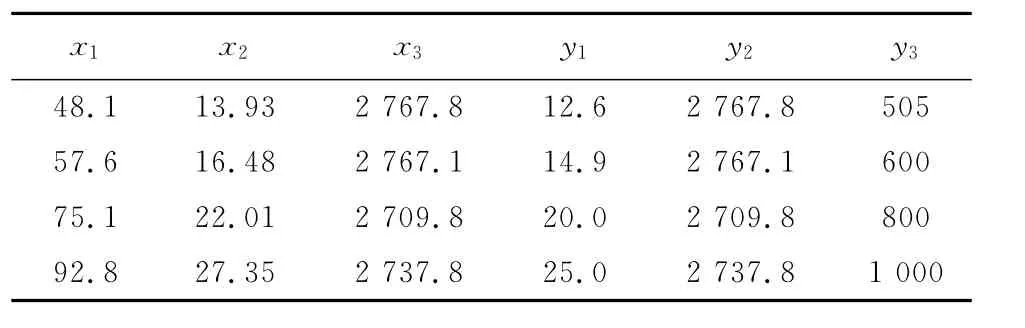
表2 机组静态工作点的实测数据Tab.2 Measured data of the unit at static work points

对直流炉机组协调控制系统的反馈控制器的设计，采用多变量PI控制器，其形式为

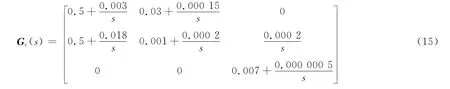
4 仿真分析

根据上述直流炉机组协调控制系统前馈－反馈控制的思路，搭建仿真框图，进行仿真实验.假定在t＝0s时，系统稳定于某一工作点.

第1种情况：输出参数的给定期望值为［yd1＝12.6，yd2＝2 767.8，yd3＝505］.在t＝100s时rB受到幅值为5的阶跃扰动；在t＝1 100s时，主蒸汽压力的设定值yd1由12.6 MPa变为18.0 MPa.系统的输出响应曲线如图2所示.图中实线为基于稳定逆的前馈－反馈控制结构的控制效果，虚线为基于状态反馈线性化的非线性内模结构的控制效果.通过比较可以看出，在基于稳定逆的前馈－反馈控制中，rB的扰动导致3个输出参数均发生较大的动态改变，相较于基于状态反馈线性化的非线性内模结构的控制方法，rB对这3个参数中的主蒸汽压力的干扰作用尤其明显.此外，在对主蒸汽压力的设定值跟踪上，基于稳定逆的前馈－反馈控制结构不仅跟踪结果准确，速率也较快，但无法完全消除对汽水分离器出口蒸汽比焓和输出功率的耦合作用.

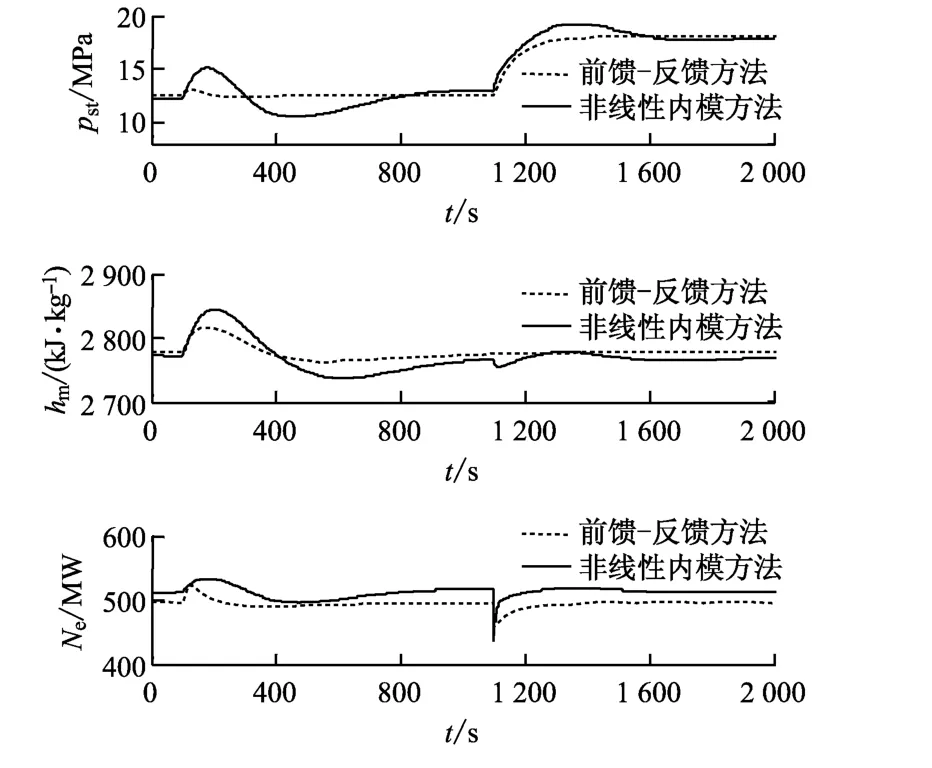
图2 第1种情况下的输出响应曲线Fig.2 Output response curve in case 1

同时给出第1种情况下输入量uB、qm，fw和ut的变化曲线，如图3所示.结合表1中的3组静态工作点，与基于状态反馈线性化的非线性内模结构的控制方法相比，在幅值上，基于稳定逆的前馈－反馈控制方法的3个输入量uB，qm，fw和ut在稳定状况下具有准确度高的优势，但存在动态波动时间长的问题.

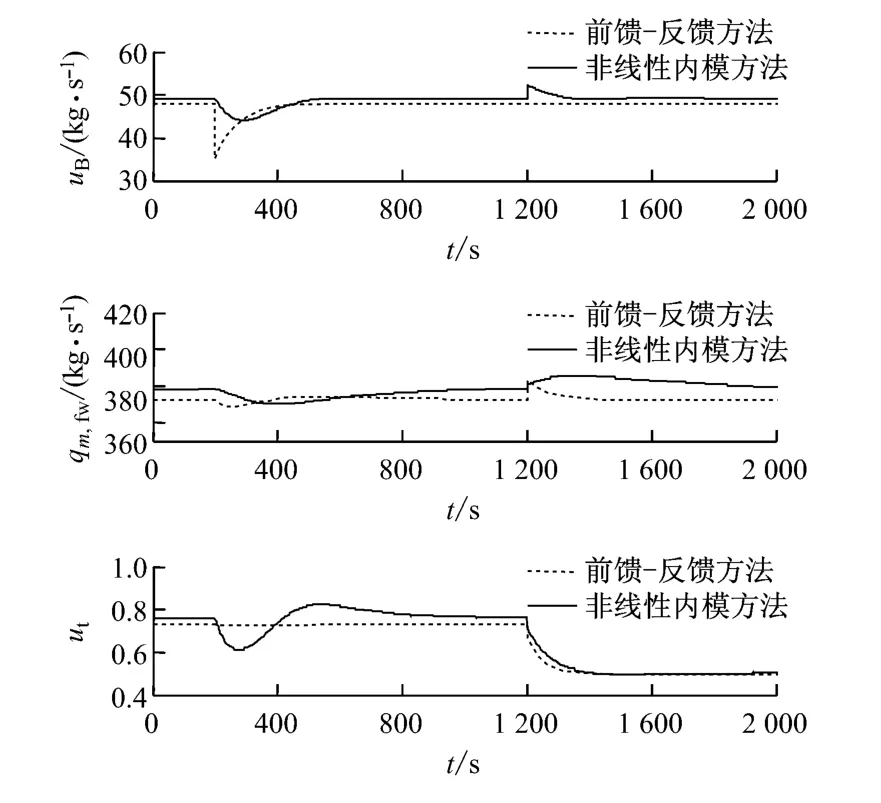
图3 第1种情况下的输入量变化曲线Fig.3 Input variation curve in case 1

第2种情况：输出参数的给定期望值为［yd1＝20.0，yd2＝2 709.8，yd3＝800］.在t＝100s时pm受到幅值为3的阶跃扰动；在t＝1 100s时，汽水分离器出口蒸汽比焓的设定值yd2由2 709.8kJ／kg变为2 719.8kJ／kg.系统的输出响应曲线如图4 所示.由图4可以看出，pm的扰动使得基于稳定逆的前馈－反馈控制与基于状态反馈线性化的非线性内模结构的控制中的pst与hm产生了幅值接近的波动，但基于稳定逆的前馈－反馈控制中这两者的影响时间更长.此外，基于稳定逆的前馈－反馈控制对于汽水分离器出口蒸汽比焓的设定值跟踪迅速，稍有超调，同时有效地消除了输出功率与主蒸汽压力的耦合作用.

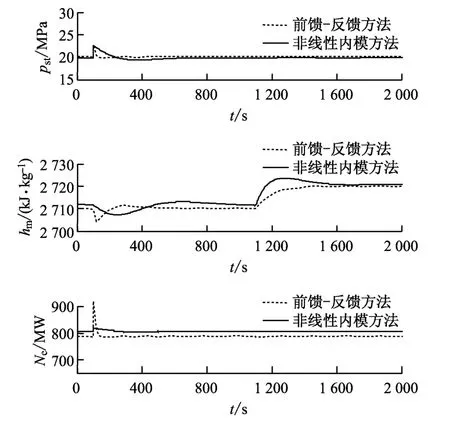
图4 第2种情况下的输出响应曲线Fig.4 Output response curve in case 2

在图5所示的第2种情况下输入量uB、qm，fw和ut的变化曲线中，基于稳定逆的前馈－反馈控制中总给水质量流量的数值明显大于基于状态反馈线性化的非线性内模结构控制方法中的这一参数.同样对照表1中的静态工作点数据可以发现，应用本文方法所得到的输入量值更为精确，并且在这一情况下其波动不明显.

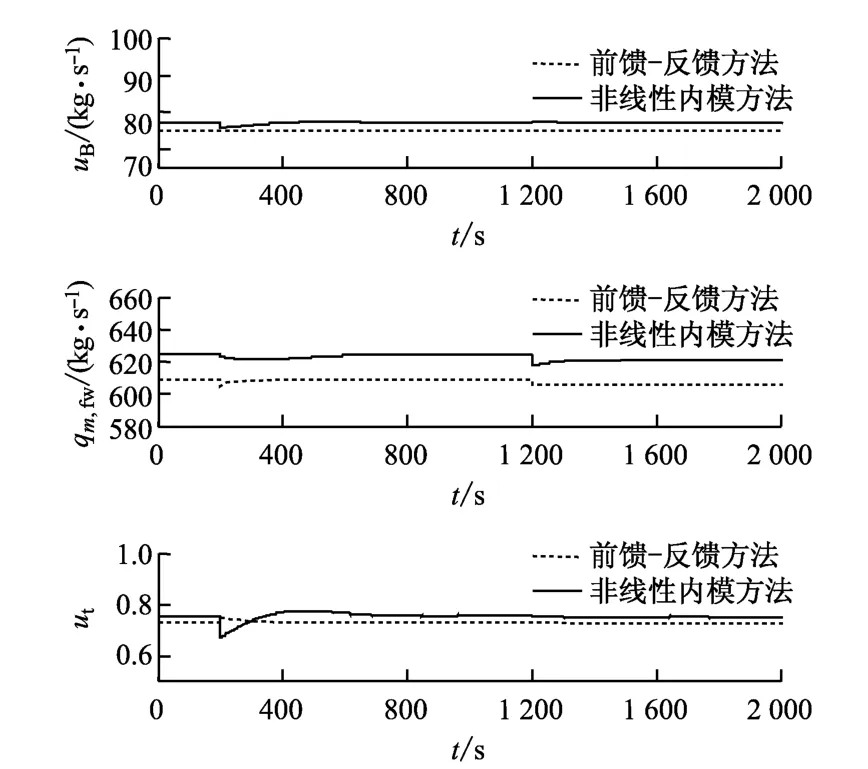
图5 第2种情况下的输入量变化曲线Fig.5 Input variation curve in case 2

第3种情况：输出参数的给定期望值为［yd1＝25.0，yd2＝2 737.8，yd3＝1 000］.在t＝100s时hm受到幅值为10的阶跃扰动；在t＝1 100s时，输出功率的设定值yd3由1 000 MW 变为1 100 MW.系统的输出响应曲线如图6所示.从幅值上看，hm对pst、hm和Ne的干扰作用均不明显.基于稳定逆的前馈－反馈控制方法在跟踪输出功率设定值时采用改变汽轮机调节门开度的方式，具有负荷响应速度快且跟踪结果准确的优势，但也引起了主蒸汽压力与汽水分离器出口蒸汽比焓在一段时间内的波动.

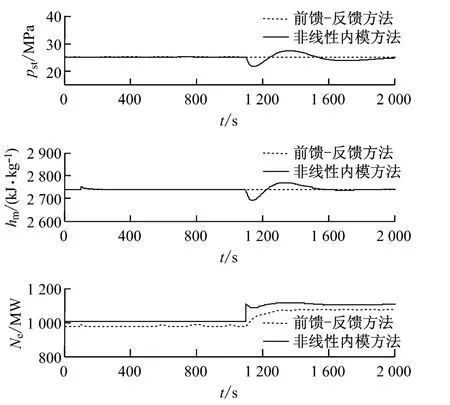
图6 第3种情况下的输出响应曲线Fig.6 Output response curve in case 3

图7 给出了第3种情况下的输入量uB、qm，fw和ut的变化曲线，对比基于状态反馈线性化的非线性内模结构的控制方法，基于稳定逆的前馈－反馈控制中的3个输入量在输出功率的设定值阶跃上升时均作出迅速改变，从而加快了负荷响应速度，但会引起汽轮机调节门开度的较大波动.

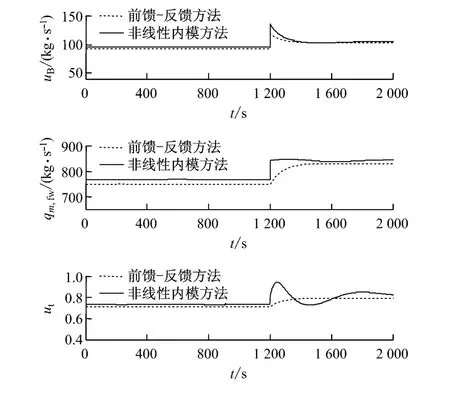
图7 第3种情况下的输入量变化曲线Fig.7 Input variation curve in case 3

从上述3组直流炉机组输出参数的变化曲线可以看出，基于稳定逆的前馈－反馈控制结构的协调控制系统，在某一输出参数设定值发生改变时能够迅速、准确地进行跟踪，还可在一定程度上消除对其他输出参数的耦合作用；然而对不同状态变量扰动的抑制作用不如基于状态反馈线性化的非线性内模结构的抑制作用明显.

通过3种情况下的输入量变化曲线可以看出，基于稳定逆的前馈－反馈控制结构的输入量值比基于状态反馈线性化的非线性内模结构的控制方法中输入量值的稳态准确度高，变化速度也更快，存在的不足是幅值的动态波动偏大，这一情况对于实际系统中调节阀等执行器设备的维护较为不利.另外仿真过程中并没有对控制量的变化速率进行限制，这一点也可能会影响到对比实验的效果，是需要进一步考虑的问题.

5 结 论

（1）直流炉机组简化模型是设计稳定逆系统的基础.在保证一定精度的前提下，对直流炉机组模型进行简化，使其稳定逆解存在，进而构造并求取逆系统.这对于其他非线性控制系统的分析与设计具有一定的借鉴意义.

（2）基于稳定逆的前馈－反馈控制结构对非线性的直流炉机组具有良好的适用性：一方面稳定逆问题的求解减弱了机炉被控对象非线性和强耦合特性对协调控制系统控制品质的影响；另一方面，基于稳定逆的前馈－反馈控制结构具有较为突出的设定值跟随能力.

（3）对于基于稳定逆的前馈－反馈控制结构的稳定性与抗干扰能力，反馈控制器的性能起着决定性的作用.笔者选用的多变量PI控制器在消除耦合以及抗干扰方面的作用不十分明显.下一步可深入研究更为有效的控制器，改善这一方案的控制品质.

［1］ ÅSTRÖM K J，BELL R D.Drum－boiler dynamics［J］.Automatica，2000，36（3）：363－378.

［2］ 曾德良，闫姝，孙伟毅，等.直流炉机组燃煤发热量信号测量模型［J］.动力工程学报，2012，32（7）：528－531.ZENG Deliang，YAN Shu，SUN Weiyi，et al.Heat value measurement of coal fuel for a once－through boiler［J］.Journal of Chinese Society of Power Engineering，2012，32（7）：528－531.

［3］ 闫姝，曾德良，刘吉臻，等.直流炉机组简化非线性模型及仿真应用［J］.中国电机工程学报，2012，32（11）：126－134.YAN Shu，ZENG DeLiang，LIU Jizhen，et al.A simplified non－linear model of a once－through boilerturbine unit and its application［J］.Proceedings of the CSEE，2012，32（11）：126－134.

［4］ TAN Wen，NIU Yuguang，LIU Jizhen.Robust control for a nonlinear boiler－turbine system［J］.Control Theory ＆Applications，1999，16（6）：863－867.

［5］ WU J，NGUANG S K，SHEN J，et al.Robust H∞tracking control of boiler－turbine systems［J］.ISA Transactions，2010，49（3）：369－375.

［6］ 房方，刘吉臻，谭文.单元机组协调系统的非线性内模控制［J］.中国电机工程学报，2004，24（4）：195－199.FANG Fang，LIU Jizhen，TAN Wen.Nonlinear internal model control for the boiler－turbine coordinate systems of power unit［J］.Proceedings of the CSEE，2004，24（4）：195－199.

［7］ YU T，CHAN K W，TONG J P，et al.Coordinated robust nonlinear boiler－turbine－generator control systems via approximate dynamic feedback linearization［J］.Journal of Process Control，2010，20（4）：365－374.

［8］ BOLEK W，SASIADEK J，T.Adaptive backstepping control of a power plant station model［C］／／15th Triennial World Congress of the International Federation of Automatic Control.Barcelona，Spain：IFAC，2002.

［9］ 黄祖毅，李东海，姜学智，等.机炉协调的增益调度伺服系统［J］.中国电机工程学报，2003，23（10）：191－198.HUANG Zuyi，LI Donghai，JIANG Xuezhi，et al.Gain scheduled servo system for boiler－turbine unit［J］.Proceedings of the CSEE，2003，23（10）：191－198.

［10］ 张铁军，吕剑虹，华志刚.机炉协调系统的模糊增益调度预测控制［J］.中国电机工程学报，2005，25（4）：158－165.ZHANG Tiejun，LÜ Jianhong，HUA Zhigang.Fuzzy gain scheduled model predictive control for boiler－turbine coordinated system［J］.Proceedings of the CSEE，2005，25（4）：158－165.

［11］ 房方，谭文，刘吉臻.机炉协调系统的非线性输出跟踪控制［J］.中 国 电 机 工 程 学 报，2005，25（1）：147－151.FANG Fang，TAN Wen6，LIU Jizhen.Nonlinear output tracking control for the coordinated system of boiler－turbine units［J］.Proceedings of the CSEE，2005，25（1）：147－151.

［12］ 闫姝.超超临界机组非线性控制模型研究［D］.北京：华北电力大学，2013.

［13］ GRAICHEN K，HAGENMEYER V，ZEITZ M.A new approach to inversion－based feedforward control design for nonlinear systems［J］.Automatica，2005，41（12）：2033－2041.

［14］ DEVASIA S，CHEN D，PADEN B.Nonlinear inversion－based output tracking［J］.IEEE Transactions on Automatic Control，1996，41（7）：930－942.

［15］ 赵为光，夏国清，杨莹，等.汽包炉单元机组的滑压工况通用非线性输出跟踪控制［J］.中国电机工程学报，2012，32（11）：118－125.ZHAO Weiguang，XIA Guoqing，YANG Ying，et al.Universal non－linear output tracking control for the drum－boiler－turbine unit under sliding pressure conditions［J］.Proceedings of the CSEE，2012，32（11）：118－125.