一种电液负载模拟器多余力的结构补偿方法

赵书尚，孙淑瑞，李阁强

(河南科技大学 机电工程学院，河南 洛阳 471003)



一种电液负载模拟器多余力的结构补偿方法

赵书尚，孙淑瑞，李阁强

(河南科技大学 机电工程学院，河南 洛阳 471003)

电液负载模拟器属于典型的被动式电液力伺服系统。为抑制和消除系统内固有的强多余力干扰，本文突破传统的从干扰补偿的角度消除多余力的方法，建立位置系统和加载系统耦合在一起的单输入双输出系统数学模型，分析研究被动式电液力伺服系统的力/位耦合机理并以结构解耦为出发点，提出一种采用复式结构伺服马达进行同步结构解耦的加载新原理，以此来消除系统中的多余力。仿真结果表明：此方法可以有效地消除小梯度加载时负载模拟器的多余力。

被动式；电液负载模拟器；复式结构伺服马达；结构补偿

0 引言

在早期飞行器研制过程中，往往需要多次进行具有自破坏性的全实物现场试验，这种试验不仅不具备可控性且难以得到准确完整的试验数据。为克服全实物现场试验的缺陷，电液负载模拟器应运而生，它可以用于实验室条件下半实物地模拟承载系统所受载荷，对承载系统进行载荷性能测试以保证产品性能，具有良好可控性及低破坏性，且试验可以多次重复，方便记录，多组数据可进行对比分析[1]。

然而，电液负载模拟器系统内存在固有的强多余力干扰，它的存在降低了电液负载模拟器的频响与精度[2]，为提高电液负载器性能，如何消除多余力干扰成为国内外众多学者研究的关键问题。目前，消除多余力的方法主要分为控制补偿与结构补偿两类：控制补偿方法调节比较方便，如神经网络控制方法[3]、混合灵敏度控制方法[4]等；结构补偿方法[5]不易受外界因素影响，抗干扰能力强，如双阀流量补偿方案、同步反向补偿方案[6]等。本质上，以上方法均是将负载模拟器的多余力看作是一种干扰，从干扰补偿的角度出发抑制和消除多余力。本文将多余力视为电液负载模拟器加载模块与被加载模块之间的力/位耦合，从如何解除耦合出发，提出一种基于复式伺服马达的同步结构解耦方法，并利用AMEsim建立模型并仿真，基于仿真结果证实此种方法的合理性及有效性。

1 负载模拟器数学模型

1.加载马达；2.扭矩传感器；3.刚性连接轴;4.承载马达;5.角位移传感器；6.承载系统伺服阀;7.数据采集卡;8.加载系统伺服阀;9.计算机。

1.1 负载模拟器工作原理

图1为负载模拟器的运行原理图[7]。由加载马达、加载系统伺服阀、扭矩传感器构成了负载模拟器的加载模块，承载马达、承载系统伺服阀、角位移传感器构成了负载模拟器承载模块。加载模块接收力矩信号，承载模块接收角位移信号，两个模块分别通过相应的传感器实现闭环反馈。

1.2 负载模拟器数学模型

将负载模拟器的加载模块与加载对象模块均看作阀控马达系统，应用传统假设[8]，将加载马达与被加载马达的结构参数看作一样，从而得出加载模块、承载模块及整个负载模拟器的方块图。

1.2.1 加载模块方块图

将整个加载对象模块看作是加载模块外部的等效负载。在不考虑非线性和油液质量影响的前提下，阀的线性化方程、加载马达的流量连续性方程以及力矩的平衡方程分别见式(1)～式(3)。

(1)

QL=KqXv-KcPL；

(2)

T=PLDm=Jms2θm+Bmsθm+G(θm-θ1)，

(3)

式中：QL为加载伺服阀的负载流量，m3/s；Kq为加载伺服阀的流量增益，m2/s；Xv为加载模块伺服阀的阀芯开口量，m；Kc为加载模块伺服阀流量-压力系数，m5/(N·s)；PL为加载马达腔的负载压力，N/m2；Dm为加载马达的理论排量，m3/rad；θm为加载马达角位移，rad；Ctm为加载马达总泄漏系数，m5/(N·s)；Vm为加载马达腔和连接管道的总容积，m3；βe为有效容积弹性模量，N/m2；T为扭矩传感器输出力矩，N·m；Jm为加载马达转动惯量，kg·m2；Bm为加载马达黏性阻尼系数，N·ms/rad；s为复频率；G为连接轴扭转刚度，N·m/rad；θ1为承载系统角位移，rad。

一般情况下，伺服阀的传递函数可以简化为二阶振荡环节。故加载模块的伺服阀传递函数可表示为式(4)。同时，将伺服放大器、扭矩传感器看做比例环节，分别列出式(5)和式(6)。

(4)

(5)

(6)

式中：Q为伺服阀输出流量，m3/s；I为伺服阀的输入电流，A；Ka为控制器增益，A/V；Ksv为伺服阀流量增益，m3/(s·A)；ωsv为伺服阀的固有频率，rad/s；εsv为伺服阀阻尼因数；Kf为扭矩传感器转换系数，V/(N·m)；U为扭矩传感器的输出电压，V；T为扭矩传感器输出力矩，N·m。

经整理，得到加载模块的方块图，如图2所示。图2中，Kce为加载模块总流量-压力系数；Tr为指令力矩信号。

图2 加载模块方块图

1.2.2 承载模块方块图

承载模块是一个电液位置伺服模块，它的3个基本方程以及伺服阀、伺服放大器传递函数与加载模块一致，见式(1)～式(5)，各个参数物理意义相同，以下用下标为1的参数表示对应的承载模块参数。把角位移传感器当作比例环节，其传递函数见式(7)。经整理得到承载模块的方块图，如图3所示。图3中，θr为指令角位移信号。

(7)

其中：Kb为角位移传感器转换系数，V/rad；U为角位移传感器输出电压，V；θf为角位移传感器测得的角度，rad;推导过程不再详述。

1.2.3 负载模拟器系统方块图

加载模块方块图与承载模块方块图表征了负载模拟器力/位耦合机理。加载模块输出力矩由两方面决定：其一是加载模块的给定加载力矩；其二是由承载模块马达角位移引起的耦合力矩。与此同时，承载模块输出角位移也由两部分构成：其一为承载模块的给定角位移；其二为加载模块输出力矩引起的耦合角位移。承载与加载模块之间相互影响，引起了强的力/位耦合。

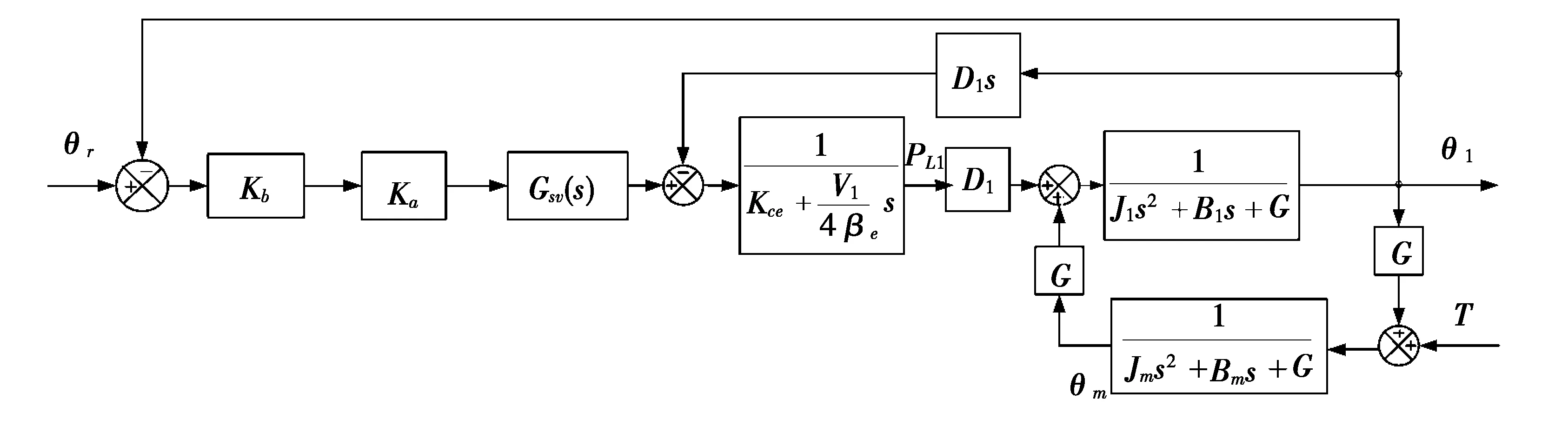
图3 承载模块方块图

2 采用复式伺服马达的结构解耦方法

2.1 采用复式伺服马达作为加载装置的负载模拟器运行原理

1.角位移传感器;2.复式伺服马达;3.扭矩传感器;4.连接轴;5.承载马达;6.角位移传感器;7.承载系统伺服阀;8.加载系统伺服阀;9.计算机;10.数据采集卡。

采用复式伺服马达作为加载装置的系统工作原理图[9]如图4所示。图4中，2为复式伺服马达，为表达清晰，将复式伺服马达拆为两个部分，左侧为同步马达，右侧为加载马达，实际马达采用复合结构，同步马达与加载马达嵌套在一起，为一个马达，称为复式伺服马达；其他组成部分的意义与图1相同。

2.2 采用复式伺服马达进行同步结构解耦的原理

加载马达转子的一端与承载马达转子伸出轴刚性连接。位于承载马达上的角位移传感器记录承载马达的转角位移，与此同时，同步马达转子上也安装有角位移传感器记录其马达转角位移，通过信号线将角度信号引入控制器，使承载马达转角位移与同步马达转角位移相等。如此，则承载马达与同步马达处于相对静止，这时候加载马达给承载马达加载力或者力矩就变成了主动加载。从系统方块图(见图4)分析结果上看：承载系统角位移引起了加载系统的耦合力(矩)，若两者相对静止，则相当于没有承载系统角位移引起的耦合力(矩)，从而达到了解耦的目的。因此，加载模块同步马达与承载模块承载马达的同步程度直接影响耦合的解除程度。

3 采用复式伺服马达同步解耦方法的AMESim仿真分析

利用AMEsim中的cam phaser chambers(凸轮相位器室)来模拟马达、液压孔模拟马达的内泄，回路中引入反馈信号，保证复式伺服马达中的同步马达与承载模块中的承载马达实现同步运动。由于小梯度加载是被动式电液力伺服系统的难点，本文将以小梯度加载为研究对象，分析采用复式伺服马达作为加载装置是否可以有效消除负载模拟器的力/位耦合。

取加载梯度为4 N·m/(°)，连接轴刚度4 N·m/(°)，对负载模拟器施加不同频率的角位移信号，在3 Hz、15 Hz频率下，承载模块和加载模块的响应曲线见图5。为更清楚地区分各个曲线，使用相同的横坐标、不同的纵坐标。角位移响应曲线图中，指令曲线对应A纵坐标，承载马达响应对应B纵坐标，同步马达响应对应C纵坐标；力矩响应曲线图中，指令曲线对应A纵坐标，输出力矩响应对应B纵坐标。图5a和图5b分别表示在3 Hz频率下的角位移与力矩响应。由图5a和图5b可以看出：加载模块同步马达与承载模块承载马达同步性很好，幅值几乎相同，相位滞后很小，解耦很彻底，力矩曲线跟随很好。图5c和图5d分别表示在15 Hz频率下的角位移和力矩响应。由图5c和图5d可以看出：加载模块同步马达与承载模块承载马达之间略有不同步，因此力矩曲线跟随略差。综上所述，低频段采用复式同步伺服马达能够有效地解除负载模拟器的力/位耦合。加载模块的跟踪性能随给定信号频率的增加略有下降，这与未加入任何算法进行精密控制，仅依靠自身反馈有关。但是在15 Hz频率下仍能保证幅值的衰减在10%以内，相位的滞后在10°以内，是满足“双十”指标的。

图5 角位移与力矩响应曲线图

4 结论

将负载模拟器看作是单输入双输出的伺服系统建立了数学模型，分析了负载模拟器力/位耦合机理，即：加载模块的输出力矩受承载模块角位移影响，与此同时，承载模块角位移又受加载模块输出力矩的影响，两者相互影响，相互作用。为解除耦合，提出了一种基于复式伺服马达进行同步结构解耦的方法，小梯度加载下的仿真分析结果表明使用该方法可以有效地解除耦合。

[1] 李阁强,李水聪,黄飞.阀控非对称缸被动式电液力伺服系统的解耦控制研究[J].机床与液压,2013,41(1):7-10.

[2] 李阁强.电液负载模拟器关键技术的研究[D].哈尔滨:哈尔滨工业大学,2006.

[3] 王燕山,李运华,王益群.基于Adaline神经网络负载模拟器的研究[J].机床与液压,2008,36(3):129-130.

[4] 王经甫,叶正茂,张辉,等.基于LMI的H∞控制在电液负载模拟器中的应用[J].机床与液压,2007,35(5):169-171.

[5] 邵俊鹏,李建英,王仲文,等.电液负载模拟器多余力抑制的结构控制补偿[J].电机与控制学报,2009,13(4):587-591.

[6] 邓大志.飞行器舵机被动式加载系统多余力矩抑制方法研究[D].广州:广东工业大学,2009.

[7] 张彪.电液负载模拟器多余力矩抑制及其反步自适应控制研究[D].哈尔滨:哈尔滨工业大学,2009.

[8] 李洪人.液压控制系统[M].北京:国防工业出版社,1990.

[9] 杨红艳.被动式电液力伺服系统的同步解耦控制研究[D].洛阳:河南科技大学,2013.

国家自然科学基金项目(51175148)

赵书尚(1969-),男,山东青岛人,副教授,硕士,主要从事测控系统设计、机电控制技术方面的研究.

2014-12-31

1672-6871(2015)04-0023-04

TH137

A