改进的差分自回归移动平均模型的共轭梯度参数估计法

2015-06-05刘雅宁

河南科技大学学报(自然科学版) 2015年4期

关键词：共轭收敛性参数估计

单锐，刘雅宁,刘文

(燕山大学理学院，河北秦皇岛 066004)

改进的差分自回归移动平均模型的共轭梯度参数估计法

单锐，刘雅宁,刘文

(燕山大学理学院，河北秦皇岛 066004)

为了提高差分自回归移动平均模型的拟合精度，本文结合已有的文献，借助无约束优化方法来解决此模型中的参数估计问题。主要提出了一种改进的差分自回归移动平均模型参数的优化估计法，并对提出的算法进行详细说明，在强Wolfe条件下对全局收敛性进行了证明。该方法保证了迭代计算的收敛性，并且提高了收敛的速度。数值试验结果说明：该算法是一种较为有效的方法，与其他方法比较，参数估计值更为显著，提高了预测精度。

差分自回归移动平均模型(ARIMA模型)；自回归滑动平均模型(ARMA模型)；参数估计；无约束问题；共轭梯度法；Wolfe搜索

0 引言

差分自回归移动平均模型简记为ARIMA模型[1]，其越来越广泛地应用于时间序列预测中，比如股市行情预报、地震预报、气象预报、水文预报等实际问题。但是，随着社会的发展，信息的需求量不断增多，信息技术的处理变得越来越复杂，对于预测精确度的要求越来越高。为了得到更精确的预测，获得更加准确的数据，就必须使得拟合模型显著，而模型的参数估计对于拟合显著模型起到关键性的作用。由于ARIMA模型实质可以理解为差分运算与自回归滑动平均模型(ARMA模型)的组合[1]，因此，可通过研究ARMA模型的参数估计来解决ARIMA模型的参数估计问题。传统ARMA模型预测随着预测期限的延长，预测的精度则越来越低，因此，很多研究者对ARMA模型的参数估计问题进行了分析研究[2-5]。文献[2]主要通过两次自回归模型(AR模型)的估计来实现ARMA模型的参数估计，在一定程度上克服了传统ARMA模型预测的缺点，但其预测的精度仍然不是很理想。文献[3]主要提出含参数的优化估计方法，通过利用优化的理论来解决参数估计问题，但其收敛的速度比较慢。文献[4]主要在文献[3]的二参数优化方法的基础上提出新的参数估计法，并通过实例证明了其算法的可行性，但是在一般的Wolfe搜索下步长的选择比较困难。本文在现有的研究基础上对ARMA模型的参数估计进行了改进，提出了一种新的ARMA模型参数的优化估计法。

1 含参数的混合共轭梯度法

无约束优化问题：

minf(X)，

其中：X∈n；函数f:n→1是连续可微的。共轭梯度法是解决此类问题的最常用方法，尤其在维数较大时更为有效,该方法避免了牛顿法中复杂的Hessen矩阵的求解，而且具有比较快的收敛速度。

共轭梯度法的迭代格式：

xk+1=xk+ωkdk；

(1)

(2)

其中：dk为下降搜索方向；ωk为通过线性搜索获得的步长因子；βk为标量。关于βk的常见公式有：

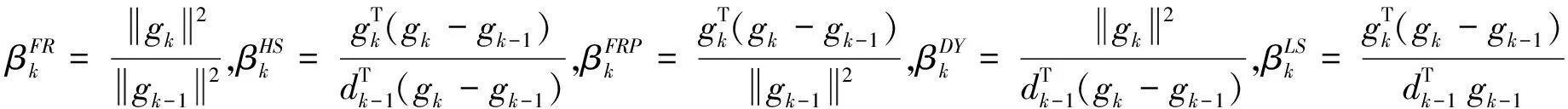
这几种方法中，PRP算法、LS算法、HS算法的数值表现比较好一些，但是其收敛性却不是很理想，甚至对于有些函数不具备收敛性；虽然FR算法、DY算法的收敛性相对于其他3种方法比较好，但数值结果却是差强人意[6-7]。

本文结合文献[4,8]提出含参数的共轭梯度法(NPY-DY(v))：

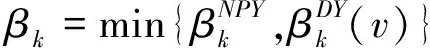
(3)

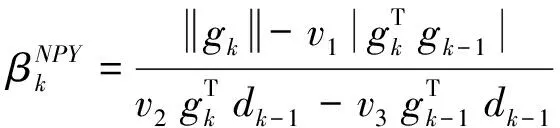
(4)

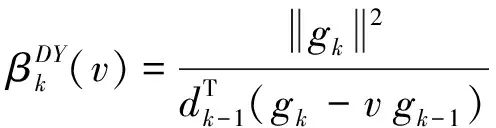
(5)

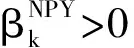
这里采用强Wolfe线搜索确定步长，即要求

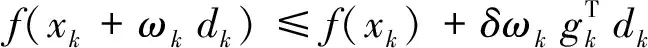
(6)

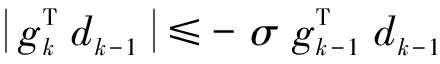
(7)

并且满足σ为常数，0<δ<σ<1。

2 ARMA模型参数的NPY-DY(v)优化估计法

2.1 参数初值的确定

考虑ARMA(p,q)模型结构[9]:

xt=φ1xt-1+φ2xt-2+φ3xt-3+…+φpxt-p-θ1εt-1-θ2εt-2-…-θqεt-q+εt，

(8)

令

Xt=[xt-1,xt-2,…,xt-p,εt-1,εt-2,…,εt-q]T；

(9)

α=[φ1,φ2,…,φp,θ1,θ2,…,θq]T，

(10)

ARMA(p,q)模型中Xt与α之间是具有非线性关系的，因此可以从优化的角度考虑将

(11)

定义为目标函数[3]。

根据无约束优化的数学模型可知：参数α的估计值问题即为求解S(α)的最优解。所以，参数估计问题就转化为求解最优值的问题。

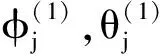
(12)

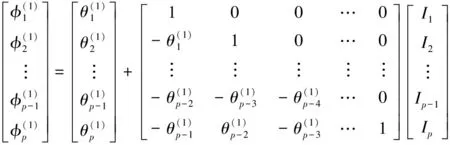
(13)

(Ⅱ)当k从p+1取到p0(p0=p+q)时，由式(12)的最后一行得：

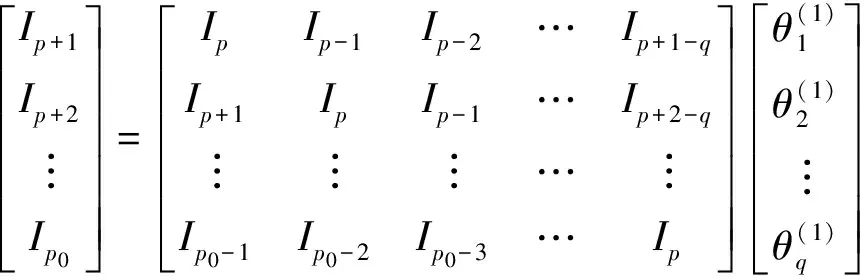
(14)

2.2 参数估计的执行步骤

步骤1 对于ARMA(p,q)模型的参数，给定如下初值结构：

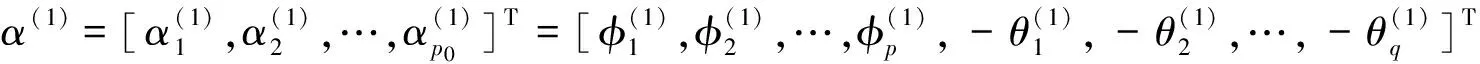
其中：p+q=p0；梯度模的允许误差δ>0。S(α)在α(1)处的梯度为：

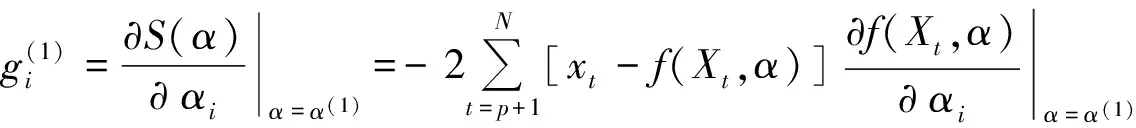
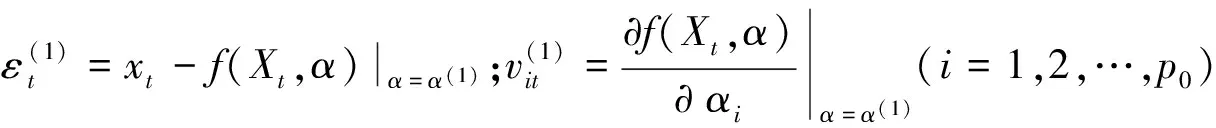
这里记为g1=-2(v(1))Tε(1),则可得S1=S(α(1)),初始搜索方向d1=-g1，置k=1。

步骤2 由强Wolfe线性搜索准则搜索确定步长ωk，由α(k+1)=α(k)+ωkdk，计算Sk+1=S(α(k+1))，gk+1=g(α(k+1))。

步骤4 若k=p，则α(1)=α(k+1),S1=Sk+1,g1=gk+1,d1=-g1,k=1,继续进行并转步骤2；若k≠p则转步骤5。

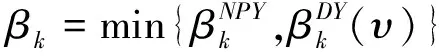
步骤6 (dk+1)Tgk+1≥0那么重复步骤4再转步骤2，否则，k=k+1转步骤2。

3 算法的下降性与全局收敛性分析

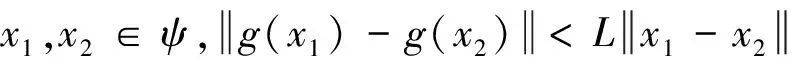
3.1 下降性

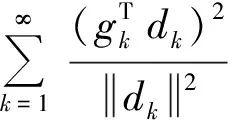
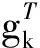
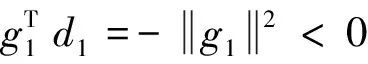
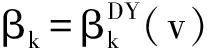
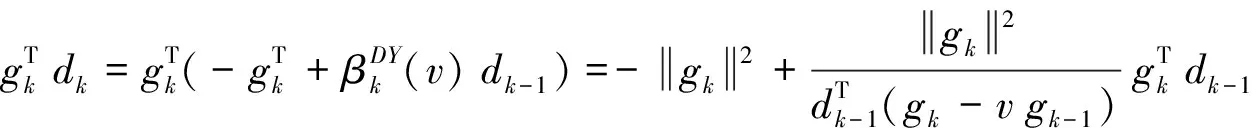
(15)

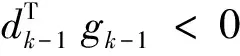
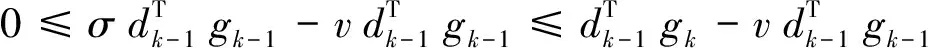
则：

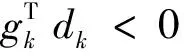
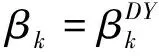
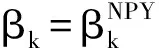
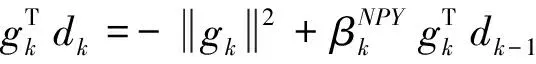
(16)

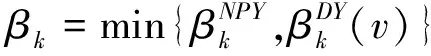
(17)

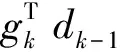
综上可知，定理得证。

3.2 全局收敛性

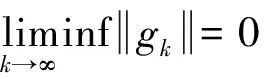
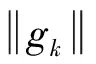
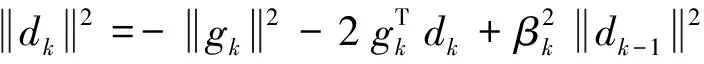
(18)

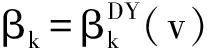
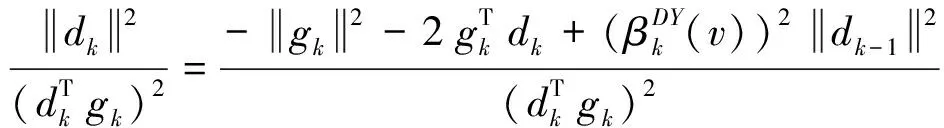
由式(5)及式(15)可得:

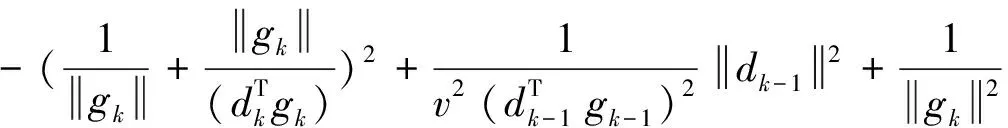
由v≥2得：

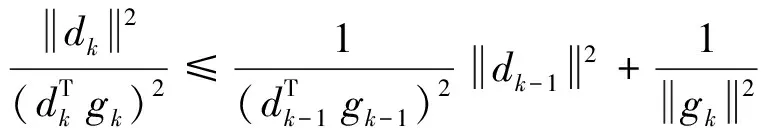
(19)

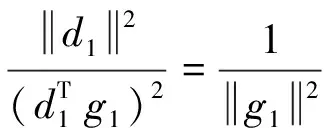
这与引理矛盾,所以定理得证。

4 数值实验与算例分析

4.1 数值实验

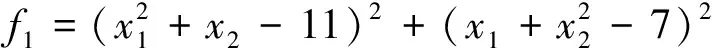
f2(x)=100(x2-x1)2+(1-x1)2初值x0=(0,0)T，最优解x*=(1,1)。

为了验证本文算法的迭代效果，选取文献[3]和本文的算法(NPY-DY(v)算法)对函数进行迭代计算，结果见表1。

选取NPY-DY(v)算法中的参数值为:v1=0.5,v2=0.2,v3=0.8,v=7.01。由表1可看出：本文算法比文献[3]算法更具有有效性。

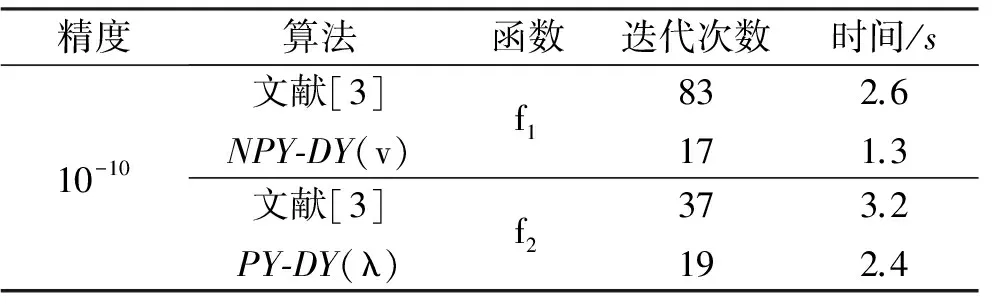
表1 数值结果

4.2 实例分析

本文选用1978年～2008年上海市人均国内生产总值(GDP)的数据[10]为例。该序列记作Xt，Xt具有明显的增长趋势，需要将其进行平稳化处理，取对数后序列记作Yt。对序列Yt进行差分运算，经过2次差分后得到平稳的序列DDYt,然后对DDYt拟合ARMA模型。初值(0.6,1),δ=0.01,σ=0.1，通过编写Matlab程序[11-12],经计算，3次迭代以后得：

α3=(0.588 9,0.971 3)。

则序列DDYt对应的模型为：

DDYt=0.588 9DDYt-1+vt-0.971 3vt-1。

对应序列Yt模型为：

Yt=2.588 9Yt-1-2.177 8Yt-2+0.588 9Yt-3+εt-0.971 3εt-1。

对Yt进行对数反变换化即可得到关于序列Xt的值。

用本文算法获得的参数模型进行预测，得到的结果如表2所示。

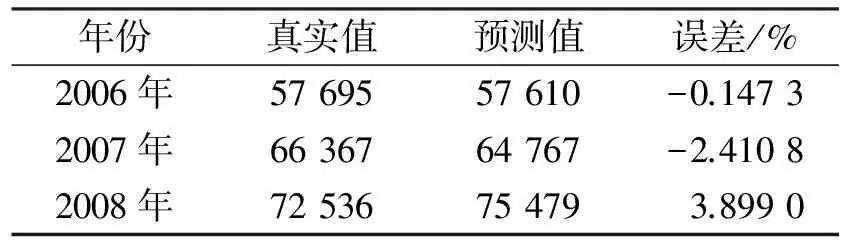
表2 预测对比

5 结论

本文主要借助无约束优化问题来解决ARIMA模型中的参数估计问题，通过结合文献[3-4],提出了一种新的模型参数优化估计法，对该算法进行详细地说明，并对算法的下降性及其在强Wolfe条件下的全局收敛性进行了证明。通过实例ARIMA模型的拟合，利用本算法对初始参数值进行迭代优化，进而得到更为显著的参数估计值，从而得到精确度更高的预测值。

[1] 王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005:65-68.

[2] 熊渊博.ARMA模型参数的分步估计法[J].湖南大学学报:自然科学版,2003,30(2):12-13,146-150.

[3] 单锐,施苏桐,刘文.基于改进共轭梯度思想的滑动平均模型参数估计优化方法[J].兰州理工大学学报:2014,40(1):145-147.

[4] 范菁.ARMA模型的两种共轭梯度参数估计法及ARIMAX模型的应用[D].秦皇岛:燕山大学,2009.

[5] 张艳萍,崔伟轩.引入动态动量因子的共轭梯度多模盲均衡算法[J].河南科技大学学报:自然科学版,2013,34(3):40-44.

[6] 杨晓辉,朱志斌,唐清干.非线性约束化的一个共轭投影梯度法及其全局收敛性[J].广西科学,2007,14(3):236-268.

[7] 施苏桐,单锐,刘文.引入扰动因子的共轭梯度算法及其收敛性[J].河南科技大学学报:自然科学版,2013,34(6):83-87.

[8] 张劲松,李红.含参数Dai-Yuan共轭梯度法及其收敛性[J].华东交通大学学报,2008,25(1):127-129.

[9] 何书元.应用时间序列分析[M].北京:北京大学出版社,2003:44-47.

[10] 叶斐.基于ARMA模型的上海市人均GDP时间序列分析与预测[J].价值工程,2010(2):231-232.

[11] 张善文,雷英杰,冯有前.MATLAB在时间序列分析中的应用[M].西安:西安电子科技大学出版社,2007:131-150.

[12] 陈国强,赵俊伟.基于MATLAB的AR模型参数估计[J].工程技术,2005,39(4):39-40.