基于贝叶斯序贯推理的自适应调制识别算法

2015-06-05付俊强赵成林

系统工程与电子技术 2015年12期

关键词：导频时变贝叶斯

付俊强，李蓉，赵成林，李斌

（1.北京邮电大学信息与通信工程学院，北京100876；2.国家无线电监测中心，北京100037）

基于贝叶斯序贯推理的自适应调制识别算法

付俊强1，李蓉2，赵成林1，李斌1

（1.北京邮电大学信息与通信工程学院，北京100876；2.国家无线电监测中心，北京100037）

提出了一种时变衰落信道下的自适应调制识别算法，设计出一种新的动态状态空间模型，来刻画信号调制方式与时变信道增益的时变特性，并引入一阶有限状态马尔可夫（finite state Markov channel，FSMC）模型来描述衰落信道；基于上述，新算法采用贝叶斯序贯推理法，充分发掘利用了其中所隐含的信道动态相关特性，实现对调制方式和时变信道增益的联合估计。仿真结果表明，新算法性能相比于传统ALRT算法有极大提升，且增加采样点数或者降低多普勒频移值都会使算法性能得到改善。

自适应调制识别；时变衰落信道；动态转移；贝叶斯序贯推理；联合估计

0 引言

调制识别作为下一代通信技术［1］中链路自适应传输的关键，目标是识别当前接收信号所采用调制方式，以及一些细节调制特征参数。调制识别技术可以大致分为两类。一类是基于特征的，可以归纳为两步，第一步是特征提取，例如高阶累积量［2］、小波变换［3］等；第二步是分类器，诸如盲聚类［4］、神经网络［5］和支持向量机［6］。另一类是基于最大似然［79］的，利用接收信号的统计似然特征，在假设信号先验信息符合均匀分布的前提下，降低了信号错误分类概率。

最大似然估计的一个关键问题需要引起重视，它严重依赖完整的信道状态信息。为了解决未知信道参数问题，文献［10］提出了一种平均似然检测（average likelihood ratio test，ALRT）算法。

考虑到移动通信环境，自适应调制编码需应用到时变衰落信道［11-12］中，因此时变衰落信道下的自适应调制识别也将带来两个挑战。第一，调制方式是随着信道的变化而不断改变的，它并不是完全独立的，因此调制方式与信道增益是相关的，先验信息不再符合均匀分布而是随着时间变化。第二，时变衰落信道也给接收信号带来很多不确定性，使得似然函数变得不精确。ALRT算法的假设前提显然不适合时变信道，而且不能实时跟踪时变衰落信道。

作为另一种克服时变衰落信道的方案，亦可借助于先验性的导频序列估计并跟踪时变衰落信道，上述方案已为LTE网络与IEEE 802.11 WLAN系统所广泛采用。然而，进一步考虑未来更加复杂的应用场景，譬如认知无线电和D2D异构形式网络，则很难在两个非协作设备间配置先验导频序列执行信道估计。此类场景下，只能采用无数据辅助或者盲估计方式来应对时变衰落信道。

鉴于上述时变衰落信道给调制识别所带来的挑战，本文提出了一种基于贝叶斯序贯推理的自适应调制识别算法，旨在解决传统ALRT算法与导频辅助估计方案在未来复杂应用场景中所面临的问题。基于新提出的动态状态空间模型［13］（dynamic state-space model，DSM），充分利用时变信道的先验转移特性，设计了一种新的贝叶斯序贯推理算法，通过对信道状态增益和调制方式联合估计来达到自适应调制识别的效果。通过实验仿真，将新方案与现有ALRT方案和导频辅助信道估计方案进行了对比，验证了所提方案的有效性。

1 系统模型

1.1 自适应调制

假设时变衰落信道服从莱斯衰落信道特性，信道衰落增益服从莱斯分布，如式（1）所示：

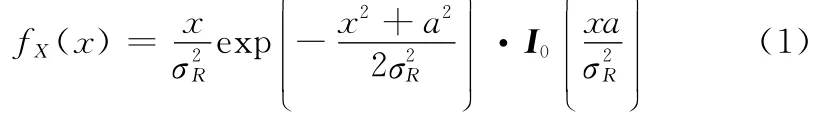
式中，x表示信道衰落增益；σ2R表示莱斯分布的方差；a表示主径幅度；I0（·）为零阶贝塞尔函数。为了实现自适应调制，将信道增益划分成K个离散状态，须满足K≥3，根据信道增益来进行不同调制方式的选择，如图1所示，其中图1右侧为莱斯概率密度分布图。

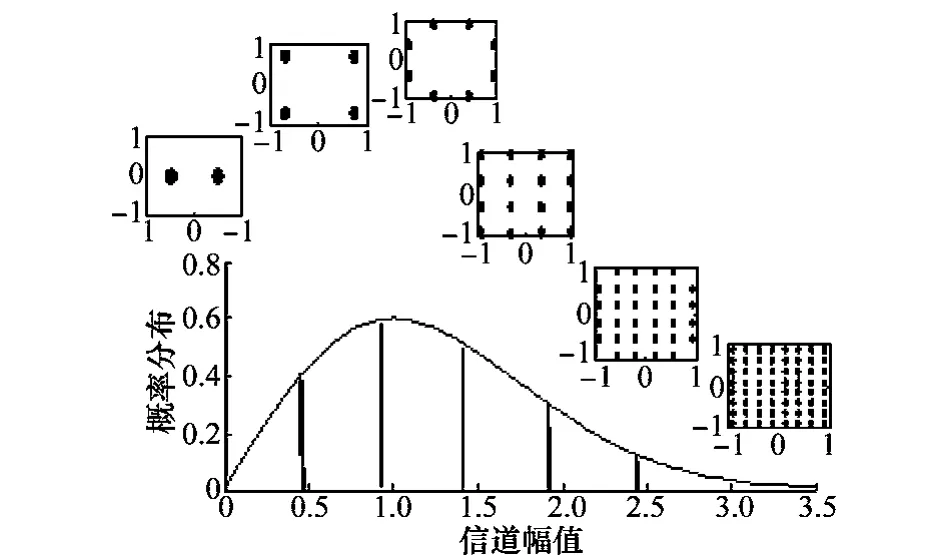
图1 时变衰落信道下的自适应调制模型

1.2 DSM模型

为了更好地应对时变衰落信道下的自适应调制带来的挑战，建立一种全新的时变衰落信道下自适应调制识别的DSM模型如式（2）～式（4）所示：

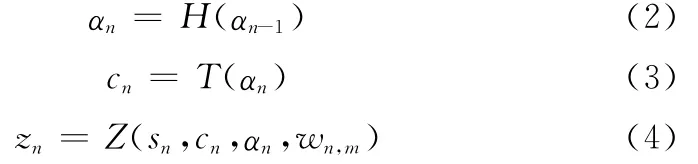
式中，αn表示第n个时刻的信道衰落幅度增益，也按照特定状态转移函数H（·）进行更新；cn表示第n个时刻的信号调制方式，sn表示第n个时刻发送的原始星座图信号点，按照一定的映射函数T（·）进行确定。下列分析对以上3个动态方程式（2）～式（4）作更进一步解释：

（1）状态转移方程H（·）：R1→R1，它基于一阶马尔科夫链建模，描述第n个时隙下的时变衰落信道增益αn→R1的动态转移过程。

（2）映射函数T（·）：R1→R1，它给出了未知调制方式cn∈R1与信道衰落增益αn之间的映射曲线关系。

（3）观测方程Z（·）［14］：RM→RM，它描述了两个隐含状态αn与cn和观测向量zn→RM之间的关系，而观测量由M个离散采样观测值zn，m（m＝0，1，…，M－1）组成。

基于DSM模型，进行如下假设：

假设1 观测过程中的噪声wn，m∈R1是n时刻下第m个采样点的独立同分布的零均值方差为σ2加性高斯白噪声，并和αn与cn相互独立。

假设2 时变衰落信道是慢衰落过程，其信道增益与传输时隙La有关，而La与最大多普勒频移值fd成反比，表示为La∞1／fd。La与感知周期Ts之间须满足La是Ts的整数倍，如图2所示。另外，它与采样点数之间是相互独立。

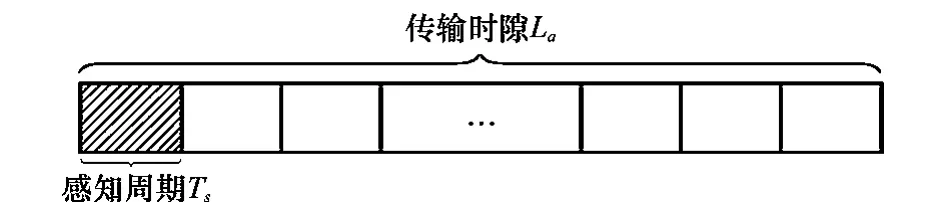
图2 信道感知模型框图

1.3 时变衰落信道模型

为了有效描述信道的动态转移特性，主要考虑一阶有限状态马尔可夫信道（finite state Markov channel，FSMC）［15］模型。首先假设状态概率向量π＝［π0，π1，…，πK－1］T，其中πk＝Pr（αn＝Ak），Ak∈A∈R1，k∈｛0，1，…，K－1｝表示第k个信道状态下的平均增益，A表示各信道平均增益集合，稳定状态下需要满足PTπ＝π［16］，PK×K＝｛Pk1→k2，i，j∈0，1，…，K－1｝可以由离散信道状态转移矩阵（probability transfer matrix，PTM）可得

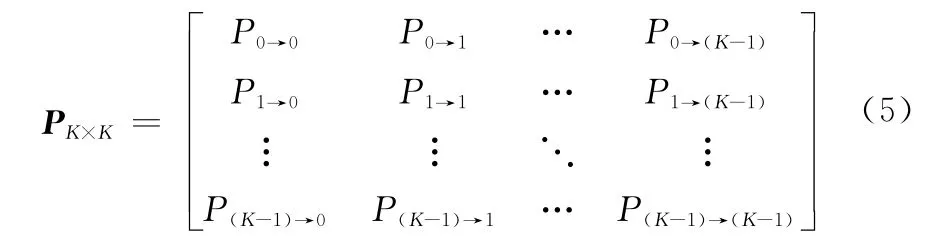
矩阵中的各个元素Pk1→k2表示从状态k1到状态k2的转移概率。

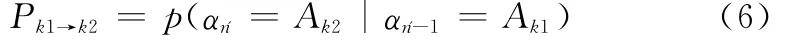
在FSMC模型中，连续信道需要被划分成多个无重叠的离散区间，Ak由一组信噪比门限值s＝｛s1，s2，…，sK｝决定，或者是一组信道增益值g＝｛g1，g2，…，gK｝s。

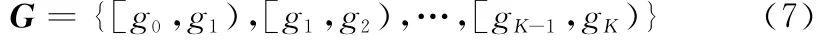
信道状态增益αn在第k个信道区间里的稳态概率由下式可得：

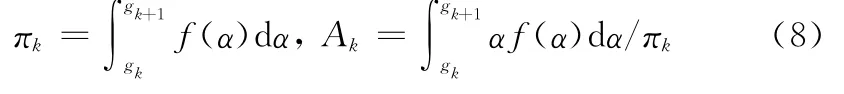
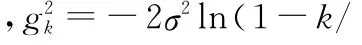
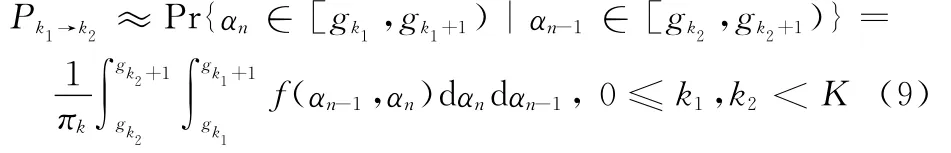
式中，f（αn－1；αn）表示时变信道的联合概率密度分布。

对于一阶FSMC，信道状态转移的可能性局限于自身和它相邻的状态，因此对于｜k1－k2｜＞1可以得到Pk1→k2＝0。实际上，可以通过计算区间跨越率，得到Pk1→k2≈Nk2／Rk1，其中Rk1＝πk2／T表示在状态k1下每秒内所含的感知周期数，其中T为符号周期。

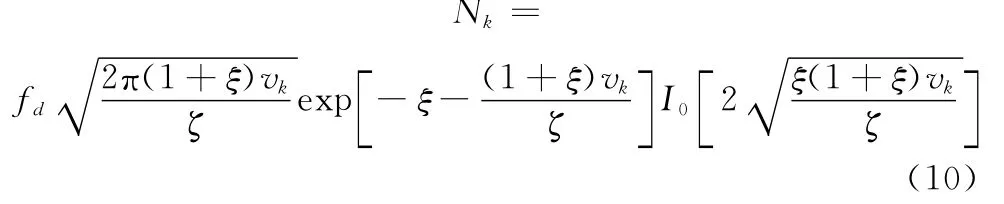
1.4 似然观测

接收端对自适应调制信号进行似然观测，它的原理就是在特定观测时间窗内，对接收信号进行采样，将观测量代入似然函数计算似然值。基带信号可以表示为

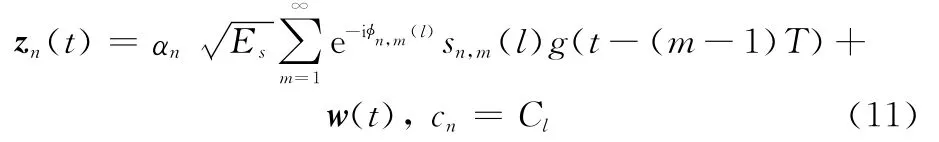
式中，i为虚部单位；Es为发射信号的平均符号能量；sn，m（l）和φn，m（l）分别为信号的幅度和相位；g（·）为成型滤波器；Cl为第l种调制方式。经过模数转换为

文献［7］中提出的最大似然算法（maximum likelihood，ML）通常假设先验信息服从均匀分布，其似然函数的对数形式如下所示：

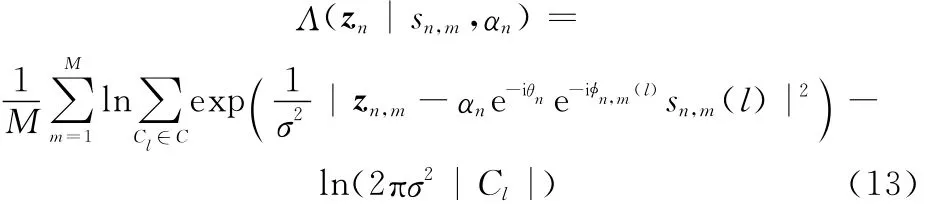
式中，M为一个感知周期内的采样点数；zn，m表示第n时刻对应的采样值；｜Cl｜表示第l种调制方式的星座点总数。

1.5 映射规则

发射端根据信道增益Ak∈A→R1动态地调整调制方式cn（l）＝Cl→R1（l＝0，2，…，L－1），所有调制方式的总数为L。而接收端对信道增益进行联合估计，依据特定的映射关系来确定调制方式。采取一对一映射，其映射关系式T（·）：R1→R1，它将信道增益与调制方式进行一一对应，即L＝K，具体关系式如下：

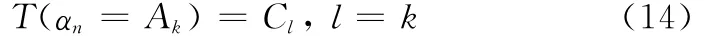
2 贝叶斯序贯推理

基于上述系统模型，进一步对两个隐含系统状态（即信道增益和未知调制方式）进行联合估计。估计检测算法主要依赖于最大后验概率和序贯推理思想，主要包含以下3个步骤：

步骤1根据特定时间窗内的信号计算似然值；

步骤2联合先验信息依据最大后验概率判决出信道增益；

步骤3最后由映射函数T（·）确定未知调制方式。

算法流程如图3所示。

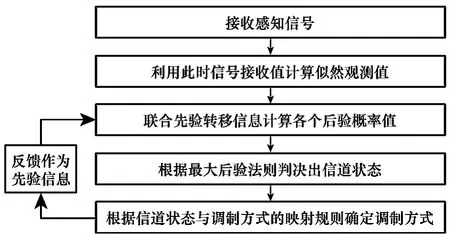
图3 接收端调制识别流程图

下面针对上述步骤进行详细介绍：

（1）似然观测

根据第1.4节中已经介绍的ML算法中似然函数式（13）计算似然值。

（2）对信道增益进行贝叶斯序贯估计

为了有效描述两个隐含状态，用向量Xn＝｛αn，cn＝T（αn）｝∈R2表示，定义n－1时刻的后验概率为pn－1｜n－1（Xn－1｜z1∶n－1），那么pn｜n（Xn｜z1∶n）表示n时刻的后验概率。

根据最大后验概率准则，通过式（15）估计出n－1时刻的信道状态。

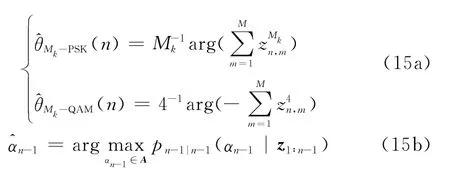
相位估计式（15a）［17］与幅度估计式（15b）是相互独立的，其中Mk为相位转移键控（phase shift keying，PSK）和正交幅度调制（quadrature amplitude modulation，QAM）的调制阶数。利用n－1时刻的估计值通过概率转移矩阵（probability transfer matrix，PTM）得到n时刻的先验转移概率，如下式

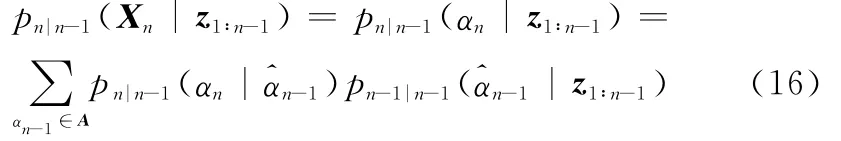
结合之前所得到的n时刻的似然值，根据式（17）求出此时各信道状态的后验概率值。

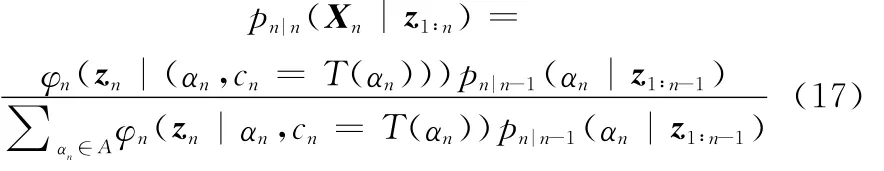
式中，似然函数φn（·）＝exp（Λ（zn｜sn，m，αn））。

（3）根据映射规则确定调制方式

映射信道状态与未知调制方式呈一一对应的关系，可以根据第1.5节中所述的映射规则得到下式：

3 仿真结果

通过Matlab仿真实验给出了莱斯时变衰落信道下的自适应调制识别与估计性能。设莱斯信道均值为1，方差为0.1，信道状态个数K＝6，发送端选用二相相移键控（binary PSK，BPSK）、正交相位偏移键控（quadrature PSK，QPSK）、8PSK、16QAM、32QAM、64QAM等，详见表1，并给出了自适应调制识别算法与现有的克服信道衰落的导频辅助估计算法和ALRT算法性能对比，突出本算法的优越性。

表1 映射关系表

3.1 不同的多普勒频移信道

仿真实验过程中，感知周期Ts内采样点个数M＝100，多普勒频移fd＝0.1，0.05，0.02，即La＝10，20，50。两种算法性能仿真结果见图4，在相同条件下，新算法比ALRT算法有更高的准确识别率，性能得到显著的提升。在识别率接近100%的信噪比区域内，不同fd下的曲线几乎重合。对于新算法，降低fd会提高识别率，而ALRT算法与fd没有明显的变化。图5为新算法在不同fd下的信道估计性能归一化均方误差（mean square error，MSE）曲线，MSE值也是随着fd的减小而不断变小。

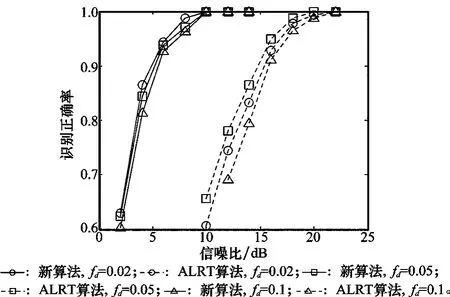
图4 不同fd值下的识别率曲线图

3.2 不同的采样点数

在其他条件保持不变的前提下，固定fd＝0.05，改变采样点数M，M＝60，100，200。实验仿真得到的算法识别性能结果如图6所示，新算法仍比ALRT算法具有更好的性能。而且随着M值的增大，识别率得到显著地提高。图7为新算法在不同M值下的信道估计性能归一化MSE曲线，M值的增加同样使得信道增益估计性能得到明显改善。

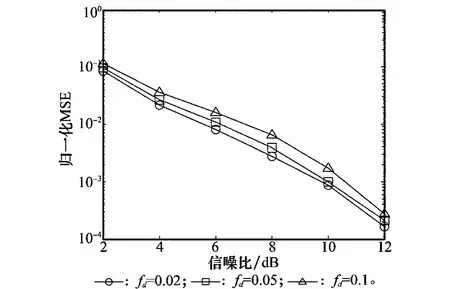
图5 新算法在不同fd值下的归一化MSE曲线图

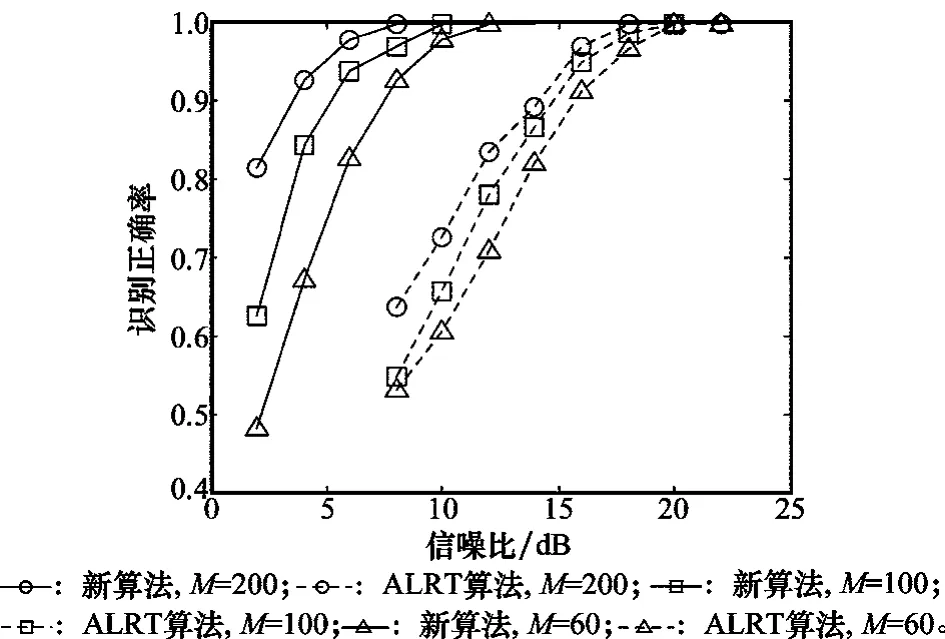
图6 不同M值下的识别率曲线图

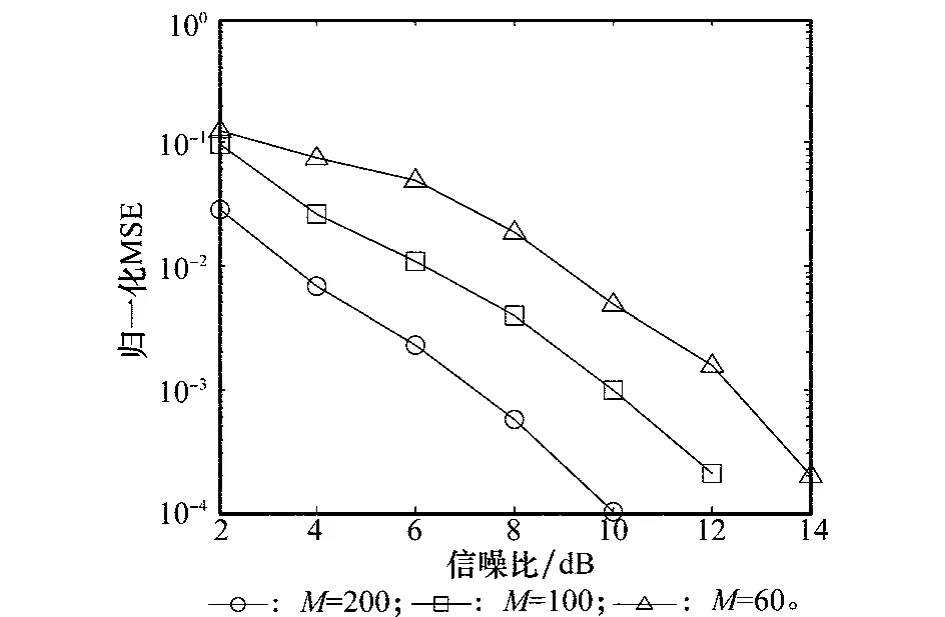
图7 新算法在不同M值下的归一化MSE曲线图

3.3 现有方案对比

现有的导频辅助估计方案，发送端每隔Ts周期发送固定复序列［1＋j，1－j，－1－j］，并且采用最小均方误差估计（minimum mean square error，MMSE）算法对信道增益进行估计。图8给出了3种算法的性能对比图，导频估计性能要优于新算法2～3 dB，ALRT算法性能最差。然而，需要注意导频辅助估计方案需要额外的先验导频序列；在某些分布式或异构网络场景中，导频辅助方案存在一定的应用局限性。相比之下，新方案不受先验性导频序列的影响，因而也具有更广泛的应用场景。

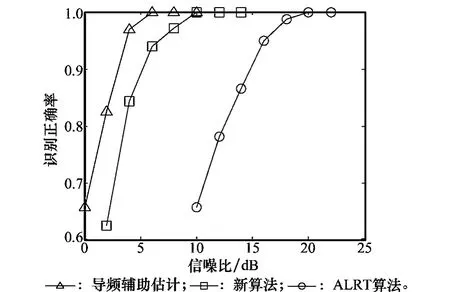
图8 fd＝0.05，m＝100下3种方案的性能对比图

最后，借助于不同算法所需的乘法次数来评估期计算复杂度。由之前的算法实现流程分析得出，新算法的时间复杂度约为O（LM（Cl＋log2Mk））；而导频辅助估计的时间复杂度约为O（LCl），ALRT算法的时间复杂度约为O（LM（KCl＋log2Mk））。可以发现，导频估计方案具有最低实现复杂度，而新算法相对于ALRT方案将更适合实时处理要求。

4 结论

针对时变衰落信道的自适应调制识别问题，区别与传统的静态系统模型，将时变信道增益建模为一种FSMC模型，并提出一种全新的基于贝叶斯序贯推理的自适应调制识别算法。新方案充分利用了时变信道状态之间的转移记忆特性，并评估特定时间窗内接收信号的似然函数，最后利用最大后验概率准则以及序贯推理思想对信道增益进行联合估计，进而根据映射准则确定调制方式。相比于ALRT算法，新算法可获得更优的识别性能，并为后续相关研究提供了一种全新理论框架，将有利于无线通信信号的信号解调、参数提取、干扰分析、信息对抗等各方面的研究。

［1］Andrews J G，Buzzi S，Choi W，et al.What will 5G be［J］.IEEE Journal on Selected Areas in Communications，2014，31（6）：1065- 1082.

［2］Liu M Z，Zhao Y，Shi L，et al.Research on recognition algorithm of digital modulation by higher order cumulants［C］∥Proc.of the 4th IEEE International Conference on Instrumentation and Measurement，Computer，Communication and Control（IMCCC），2014：686- 690.

［3］Yin SG，Liu W，Wang C.Based on the singular value decomposition fast wavelet ridge intra pulse modulation recognition［C］∥Proc.of the Applied Mechanics and Materials，2014：4933- 4940.

［4］Wang J X，Zhang L P.Blind modulation recognition algorithm for MQAM signals［J］.Journal of Electronics&Information Technology，2011，33（2）：332- 336.

［5］Albers H E.The regulation of social recognition，social communication and aggression：vasopressin in the social behavior neural network［J］.Hormones and Behavior，2012，61（3）：283- 292.

［6］Kannan R，Ravi S.Second-order statistical approach for digital modulation scheme classification in cognitive radio using support vector machine and k-nearest neighbor classifier［J］.Journal of Computer Science，2013，9（2）：235- 243.

［7］Bai D，Lee J，Kim S，et al.Near ML modulation classification［C］∥Proc.of the IEEE Vehicular Technology Conference（VTC Fall），2012：1- 5.

［8］Xu J L，Su W，Zhou M.Likelihood-ratio approaches to automatic modulation classification［J］.IEEE Trans.on Systems，Man，and Cybernetics，Part C：Applications and Reviews，2011，41（4）：455- 469.

［9］Hameed F，Dobre O，Popescu D C.On the likelihood-based approach to modulation classification［J］.IEEE Trans.on Wireless Communications，2009，8（12）：5884- 5892.

［10］Dobre O A，Abdi A，Bar-Ness Y，et al.Survey of automatic modulation classification techniques：classical approaches and new trends［J］.Communications，2007，1（2）：137- 156.

［11］Abeida H，Al-Harthi M M，Merabtine N，et al.EM and MAP methods for joint path delay and complex gain estimation of a slowly varying fading channel for CPM signals［J］.International Journal of Engineering and Technology，2014，4（5）：261- 270.

［12］Sklar B.Rayleigh fading channels in mobile digital communication systems I：characterization［J］.IEEE Communications Magazine，2002，35（7）：90- 100.

［13］Wang H S，Moayeri N.Finite-state Markov channel-a useful model for radio communication channels［J］.IEEE Trans.on Vehicular Technology，1995，44（1）：163- 171.

［14］Rabiner L R，Juang B H.An introduction to hidden Markov models［J］.IEEE Trans.on Acoustics，Speech，Signal Processing Magazine，1986，3（1）：4- 16.

［15］Sadeghi P，Kennedy R A，Rapajic P B，et al.Finite-state Markov modeling of fading channels-a survey of principles and applications［J］.Signal Processing Magazine，2008，25（5）：57- 80.

［16］Li B，Zhao C L，Sun M W，et al.Spectrum sensing for cognitive radios in time-variant flat-fading channels：a joint estimation approach［J］.IEEE Trans.on Communications，2014，62（8）：2665- 2680.

［17］Dobre O，Hameed F.Likelihood-based algorithms for linear digital modulation classification in fading channels［C］∥Proc. of the IEEE Conference on Electrical and Computer Engineering，2006：1347- 1350.

Sequential Bayesian inference based adaptive modulation recognition algorithm

FU Jun-qiang1，LI Rong2，ZHAO Cheng-lin1，LI Bin1
（1.School of Information and Communication Engineering，Beijing University of Posts and Telecommunications，Beijing 100876，China；2.The State Radio Monitoring Center，Beijing 100037，China）

Under the time-varying fading channel，an adaptive modulation recognition algorithm is presented.A new dynamic state space model is designed to describe time-varying characteristics of modulation schemes and channel gain.A first-order finite state Markov channel（FSMC）model is introduced for the fading channel.On this basis，a new algorithm，which adopts the sequential Bayesian inference method and is proposed to fully exploit the dynamic transfer characteristics of the hidden channel state，achieves joint estimation of modulation and time-varying channel gain.The simulation results prove that performance of the algorithm compared to traditional ALRT algorithms greatly improves，and increasing the number of sampling points or reducing the Doppler shift value can make the performance better.

adaptive modulation recognition；time-varying fading channel；dynamic transfer characteristics；Bayesian sequential inference；joint estimation

TN 911.7

10.3969／j.issn.1001-506X.2015.12.30

付俊强（199-2- ），男，硕士研究生，主要研究方向为统计信号处理、调制识别。

E-mail：750450554＠qq.com

李蓉（1984- ），女，工程师，博士，主要研究方向为无线通信、频谱监测与频谱管理。

E-mail：lirong＠srrc.org.cn

赵成林（1964- ），男，教授，博士，主要研究方向为信号处理、无线通信技术。

E-mail：clzhao＠bupt.edu.cn

李斌（198-5- ），男，讲师，博士，主要研究方向为统计信号估计与检测、认知无线电。

E-mail：binli＠bupt.edu.cn

1001-506X（2015）12-2860-05