一种加权傅里叶变换域通信方法

达新宇，廉 晨

（空军工程大学信息与导航学院，陕西西安710077）

一种加权傅里叶变换域通信方法

达新宇，廉 晨

（空军工程大学信息与导航学院，陕西西安710077）

为提高通信的安全性，将多项加权分数傅里叶变换（multi-terms weighted-type fractional Fourier transform，MWFRFT）与变换域通信系统（transform domain communication system，TDCS）相结合，提出一种加权傅里叶变换域通信方法。首先使用MWFRFT对原信号进行处理；然后利用混沌序列产生的伪随机相位生成TDCS基函数；最后将所得信号与基函数调制并用于隐蔽通信。为验证该方法的可行性，对信号的星座变换特性以及相关特性进行了仿真分析，结果表明，MWFRFT具有较好的星座混淆性，利用混沌映射得到的TDCS基函数相关性有所提高，因此，该方法适用于隐蔽通信。

加权分数傅里叶变换；变换域通信；隐蔽通信；扩频通信

0 引 言

加权分数傅里叶变换（weighted fractional Fourier transform，WFRFT）［1］自提出以来，在光学方面得到了广泛应用。近年来，研究者们不断扩展其形式与范围，并将其应用到通信［2-3］、信息加密［45］、图像压缩［6］等信息隐蔽领域［7］，取得了一定成果。文献［8］提出了一种离散序列的WFRFT，使信号具有了星座旋转扩散性，抗检测性良好，且比特能量均匀分布，提高了抗干扰性。然而，限于离散傅里叶变换（discrete Fourier transform，DFT）周期为4的特点，离散序列的WFRFT的加权项数固定为4。针对此，提出一种离散序列的多项加权分数傅里叶变换（multi-terms WFRFT，MWFRFT）：根据CFRFT定义提出一种离散序列的分数傅里叶变换，再利用SWFRFT中的加权系数以及Shih［1］关于基本算子的要求对离散分数傅里叶变换加权，给出了MWFRFT的定义。

变换域通信系统（transform domain communication system，TDCS）［9］是一种智能通信系统，能检测空闲频段进行扩频通信，从而有效避免了干扰，又因为其基函数相位是由伪随机序列确定的，类似于噪声，所以具有了很好的抗截获性［10］。TDCS的性能取决于基函数的性能［11］，学者们针对门限设计［12］、伪随机序列生成等多方面提出了不同的基函数设计方法，其中，采用混沌映射得到的基函数相关性能较好。

将MWFRFT与混沌映射产生的TDCS基函数相结合，既可以避免信道干扰和用户间相互干扰，又可以结合两种技术的隐蔽特性，得到抗截获性能更好的信号形式。

1 WFRFT信号

1.1 离散序列4项WFRFT信号

文献［13］根据WFRFT的形式，结合DFT特点，提出了一种离散序列的加权分数傅里叶变换，定义如下：

式中，X0，X1，X2，X3分别为序列X0的0～3次离散傅里叶变换。ωl为加权系数，与连续函数的WFRFT定义一致［14］：

式中，V＝（MV，NV），MV＝（m0，m1，m2，…，mM－1），NV＝（n0，n1，n2，…，nM－1）为参数向量；α为变换角度；M为加权项数。由于DFT周期为4，式中M＝4，离散序列的加权分数傅里叶变换也简称为4-WFRFT。DFT可以表示成矩阵乘积的形式：

式中，F为DFT的变换矩阵；N为序列X0的长度；WN＝exp（－i2π／N）。则4-WFRFT也可以表示为

推广得到X0的1～4次4-WFRFT，即S4W：

式中，S0，S1，S2，S3分别为X0的1～4次4-WFRFT，且分别为S0的0～3次DFT，则

又由旋转相加性可得W4W（α，V）W4W（－α，V）＝I，即W（α，V）＝W4W（－α，V）。则4-WFRFT的逆变换定义为

4-WFRFT可以对任意复离散序列X0进行变换，变换后的信号星座图发生旋转、扩散、分裂和混淆，具有了一定隐蔽特性。以QPSK信号为例，经过4-WFRFT变换后的信号星座变换情况如图1所示。

图1 4-WFRFT信号星座图

由图1可见，通过改变加权系数，可以使经过变换的信号在复平面上呈现出一种类高斯的分布，只有掌握所以参数信息，经过相应的逆变换，才能恢复出正确的星座图，而在参数未知的情况下将无法正确解调，从而提供了一种抗截获的信号变换形式。

同时，可以看出在某些特定点，星座图发生了有规律的旋转和分裂，并且当参数α接近0、2（4-WFRFT中α周期为4）时，星座图依然比较集中，易被检测到，所以在进行隐蔽通信时，需选择合适的变换参数。

1.2 离散序列MWFRFT信号

4-WFRFT基于离散傅里叶变换周期为4的特点进行加权，加权项数也局限为4项。为提高变换的多样性，增加变换参数，提出了MWFRFT，该变换将DFT矩阵分数化后再进行加权。过程如下：

首先，将DFT矩阵分数化。DFT周期为4，即F4＝I，现要将其周期扩展为M。根据分数傅里叶变换的思想，令p＝4／M，可以定义新的离散分数傅里叶变换：

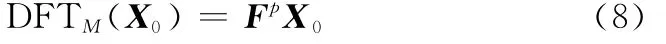
则该变换的周期为M。

再对新的离散变换进行加权，加权系数可以沿用连续函数WFRFT的加权系数，则所得的MWFRFT可表示为矩阵与向量的乘积：

推广得到：

式中，S0，S1，…，SM－1分别为S0的0～M－1次MWFRFT。与4-WFRFT相同，W（α，V）＝WMW（－α，V），则

MWDFT的逆变换为

由此得到了MWFRFT的定义。可见，该变换与原变换相比，加权项数M的选择范围更广，参数更多，增加了加权分数傅里叶变换的多样性。同时，该变换也具有星座旋转、分裂、扩散及混淆特性，经过MWFRFT的正交相移键控（quadrature phase shift keying，QPSK）信号星座图变换情况如图2所示。

图2 MWFRFT信号星座图

由图2可见，相比于4-WFRFT，MWFRFT中星座图的扩散速度更快，混淆性更好，并且随着M值的增大，α周期变长，减少了较为集中的星座图数量，更适用于隐蔽通信。

2 TDCS基函数

TDCS的核心内容是基函数生成，基函数的性质决定了通信系统的抗干扰、抗截获性能，以及频谱感知和多址接入能力，是其与其他通信系统的区别所在。基函数生成包括了幅度谱向量生成、随机相位编码、能量调整以及傅里叶反变换。

2.1 幅度谱向量

TDCS有效抵御信道及用户间干扰的根本原因是系统能够感知当前电磁环境，利用空闲频段进行信号传输，过程为：对给定阈值AT，如果某点的功率谱密度的幅值大于AT，则视为该点的频谱被已干扰或占用，将该点的幅值设置为0；若小于AT，则设置为1，由此得到由0、1构成的幅度谱向量A（ω）：式中，Ai∈｛0，1｝表示第i个采样点的幅值；N为采样点数。

2.2 伪随机相位编码

TDCS的基函数使用了伪随机相位，具有类似噪声的特性，互相关性较低，所以系统抗截获特性较好，并且具有多址接入能力。已有的伪随机相位生成方法为：先使用线性反馈移位寄存器产生m序列，再利用相位映射器对m序列进行r比特抽样后对应2r个复相位值，就构成了伪随机复相位矢量｛eiθ（k），k＝0，1，…，N－1｝，该矢量与前面的谱矢量A（ω）长度相同。

伪随机相位决定了TDCS基函数的伪随机特性，但由于普遍使用的m序列存在周期，且长度有限，限制了相位的伪随机性。针对此，文献［15］指出，可以使用长度更长，相关性能更好的混沌序列作为生成TDCS基函数的伪随机序列。文献［16］中，提出了采用双混沌序列［17］生成基函数伪随机相位的方法，通过增加一维控制参数，并结合混沌映射的混淆性，提高了基函数的伪随机特性。本文采用双混沌序列生成伪随机相位的方法，并使用两种新型混沌迭代映射方法产生伪随机相位。

首先使用3次与4次多项式混沌映射交叉迭代产生足够长的混沌序列，这两种映射是Logistic映射的变形，通过增加映射函数次数来提高映射的非线性，定义为

式中，参数范围为k∈（0.5，0.57）。

式中，参数范围为k∈（1，∞）。

在参数范围内，两种映射都达到了满映射状态，能够产生伪随机性良好的混沌序列。设定（－1，1）内的任意值作为初始值，使用两种映射交叉迭代，产生混沌序列。

然后使用4次混沌映射再产生抽头控制序列，对双混沌序列进行抽头，产生伪随机相位。通过改变混沌映射参数及初始值可以得到完全不同的伪随机相位，θ（k）∈｛0，2π／2r，4π／2r，…，2π（2r－1）／2r｝。抽头映射过程如图3所示。

图3 伪随机相位映射过程

2.3 能量调整及傅里叶反变换

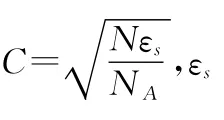
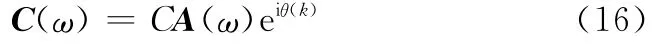
将C（ω）从频域变换到时域进行傅里叶反变换，得到基函数的时域表达式，反变换方法与幅度谱估计使用的变换方法一一对应。为与加权傅里叶变换保持一致，采用归一化的离散傅里叶反变换（inverse DFT，IDFT），即可得到时域离散形式的基函数：

式中，n＝1，2，…，N。又由：

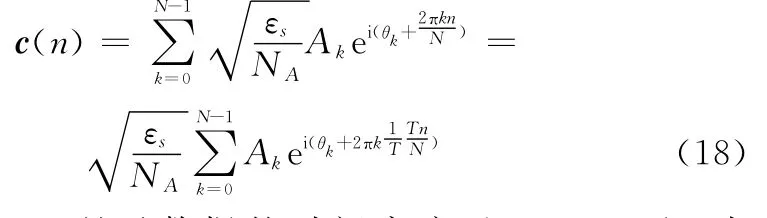
T为TDCS码元数据的时间宽度，记Δf＝1／T为TDCS信号各频率分量的间隔，根据采样定理，离散的c（n）可以看作是对连续的复基带信号c（t）进行等间隔采样获得的。取采样间隔为T／N，则基函数的时域表达式为

2.4 基函数及相关特性

根据上述步骤得到的基函数时域波形如图4所示。

图4 基函数时域波形

由图4可见，该基函数具有类似噪声的时域波形，伪随机性较好。将该基函数的相关特性与使用m序列生成伪随机相位的基函数相比，所得结果如图5所示。

由图5可见，使用双混沌交叉映射，混沌控制抽头系数生成的基函数在相关间隔为0时，相关系数接近于1，相关间隔不为0时，相关系数接近于0，且小于同等长度的m序列生成基函数，伪随机性更好，也更适用于隐蔽通信。

3 MWFRFT-TDCS信号

3.1 MWFRFT-TDCS信号调制与解调

TDCS中，双极性调制是对基函数的最简单的调制方式，通过基函数的正负表示不同码元。实质是利用基函数本身的性质进行调相。将MWFRFT与TDCS相结合，也可以采用类似的调制手法，利用TDCS基函数作为载波，通过控制基函数的幅值和相位进行扩频，信号调制解调流程图如图6所示。

图5 基函数相关特性比较

图6 MWFRFT-TDCS扩频信号调制解调流程图

图6中，a（i）为原数字信号，MWFRFT可以处理任何形式的复数，所以理论上a（i）可以为任意序列，假定a（i）为双极性复数信号，即QPSK信号。aω（i）为经过MWFRFT的信号，使用TDCS基函数c（n）作为载波对aω（i）进行扩频，得到发送信号si（n），表示为

通过信道后，接收端的接收信号为

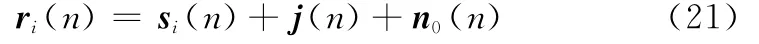
式中，j（n）为信道中的干扰信号，即使用信道进行通信的其他用户；n0（n）为加性高斯白噪声。假设系统完全同步，且收发机工作环境一致，对接收信号进行相关解调，得到解扩信号：

式中

由基函数的产生原理可知，基函数与干扰信号正交，因此J＝0，此时解扩信号简化为

对解扩信号进行幅度变换，然后进行逆MWFRFT变换，得到接收信号：

信号经MWFRFT变换后，由规则的双极性复信号变为分布在复平面上幅值不同的信号，给准确解调带来了困难，但由信息调制解调原理可见，MWFRFT-TDCS相当于对基函数进行了扩频，扩频本身具有剔除噪声的能力，且在TDCS基函数幅值向量生成过程中已经避开了干扰较大的频段，所以该方法仍然可以得到较为准确的解调信号。

3.2 MWFRFT-TDCS信号性质

MWFRFT-TDCS调制结合了具有星座扩散混淆性的MWFRFT与具有伪随机特性的TDCS基函数，实质是MWFRFT信号对TDCS基函数的扩频，由调制过程可知每个MWFRFT信号星座点都将被扩散，解决了WFRFT中部分参数变换信号星座点集中的问题。

对调制信号的星座特性进行仿真分析。以QPSK信号为例，对输入的双极性复信号进行调制，选取不同的MWFRFT参数值，所得调制信号与未调制信号的星座图作对比，结果如图7所示。

由图7可知，MWFRFT-TDCS有效地解决了星座图集中的问题，充分混淆了原有星座点，与理论分析一致，适用于隐蔽通信。

对调制信号的相关特性进行仿真分析。以QPSK信号为例，经MWFRFT变换并与混沌TDCS基函数进行调制，所得调制信号与原TDCS基函数的双极性调制信号进行对比，结果如图8所示。

由图8可知，信号先经过MWFRFT变换，再与双混沌映射产生的TDCS基函数调制后，所得信号的相关特性在相关间隔不为0时，明显小于原有的双极性TDCS调制信号，能够更好的避免用户间的相互干扰和抵御非接收方的检测识别。相关间隔等于0时，MWFRFT-TDCS信号的相关特性小于双极性TDCS调制信号，但仍明显大于间隔不为0时的相关特性，接近于1，不会影响接收信号的正确解调。

图7 信号星座图比较

图8 调制信号相关特性比较

4 结 论

文中提出了一种将MWFRFT与变换域通信系统结合的通信方式，结合了MWFRFT的混淆特性与TDCS的抗干扰抗截获特性。首先，提出将已有离散序列的4-WFRFT的加权项数扩展为M项，给出了扩展过程并对新变换的星座旋转扩散特性进行了仿真验证，分析表明新提出的MWFRFT同样具有星座旋转扩散特性，且扩散速度更快，混淆更充分。然后，针对已有的利用m序列生成伪随机相位的方法中，m序列具有周期，且长度有限的缺点，采用了一种双混沌映射产生伪随机相位的方法，并使用了两种新混沌迭代映射，得到了伪随机性良好的TDCS基函数，仿真结果表明新的基函数相关特性优于已有的m序列TDCS基函数。最后，将MWFRFT变换后的信号与新的基函数进行扩频调制，对所得调制信号的星座图及相关特性进行了仿真验证，结果表明，调制信号的星座混淆性及相关特性优于单独的WFRFT信号与双极性TDCS调制信号。

MWFRFT适用于现有的数字通信系统，加权项的扩展能够引入更多参数，提高了信号处理的多样性，增加了破解信息的难度，从信号内容方面增强了隐蔽性；采用混沌映射能够产生足够长的伪随机序列，且能够通过调整参数值控制TDCS基函数的生成，基函数良好的相关特性从波形方面提供了隐蔽性。将MWFRFT与TDCS相结合，即从内容与波形两方面对信息进行了处理，更适用于隐蔽通信。

［1］Shih C C.Optical interrelation of a complex-order Fourier transform［J］.Optics Letters，1995，20（10）：1178- 1180.

［2］Shi J，Chi Y G，Sha X J，et al.Application of weighted-type fractional Fourier transform in sampling and reconstruction［J］.Journal on Communications，2010，31（4）：88- 93.（史军，迟永钢，沙学军，等.加权分数傅里叶变换在采样重构中的应用［J］.通信学报，2010，31（4）：88- 93.）

［3］Qiu X.Performance research on hybrid carrier system based on fractional Fourier transform［D］.Harbin：Harbin Institute of Technology，2013.（邱昕.基于分数傅里叶变换的混合载波通信系统性能研究［D］.哈尔滨：哈尔滨工业大学，2013.）

［4］Feng H.Analysis of anti-interception performance of weightedtype fractional Fourier transform signal［D］.Harbin：Harbin Institute of Technology，2011.（冯红.加权类分数傅里叶变换信号的抗截获性能分析［D］.哈尔滨：哈尔滨工业大学，2011.）

［5］Mei L，Sha X J，Zhang N T.The secure communication system based on single／multi-parameter weighted-type fractional Fourier transform［J］.Journal of Yunnan University of Nationalities（Natural Sciences Edition），2011，20（5）：361- 366.（梅林，沙学军，张乃通.加权分数傅里叶变换通信系统抗参数扫描及星座分裂性能分析［J］.云南民族大学学报（自然科学版），2011，20（5）：361 -366.）

［6］Zhu Y，Shen Y F，Jiang H.Image resizing algorithm based on content partition and Fourier analysis［J］.Computer Engineering and Design，2013，34（1）：225- 229.（朱运，沈一帆，姜昊.基于内容划分和傅里叶分析的图像缩放算法［J］.计算机工程与设计，2013，34（1）：225- 229.）

［7］Bao Y Q，Deng A D，Zhao L.The speech information hiding model of transparency in fractional Fourier domain based on the wide interval of hopping［J］.Signal Processing，2010，26（10）：1544- 1551.（包永强，邓艾东，赵力.分数傅里叶域上宽间隔跳变的透明语音信息隐藏模型［J］.信号处理，2010，26（10）：1544- 1551.）

［8］Mei L，Sha X J，Ran Q W，et al.The research on the application of 4-WFRFT in communication system［J］.Science in China Series F：Information Sciences，2010，40（5）：732- 741.（梅林，沙学军，冉启文，等.四项加权分数Fourier变换在通信系统中的应用研究［J］.中国科学：信息科学，2010，40（5）：732- 741.）

［9］German E H.Transform domain signal processing study final report［R］.Reisterstown，MD：Air Force Research Laboratory，1988.

［10］Shi J，Chi Y G，Zhang N T.Principle，technology and tendency of transform domain communication system［J］.Journal of Nanjing University of Posts and Telecommunications（Natural Science），2009，29（2）：87- 94.（史军，迟永刚，张乃通.变换域通信系统：原理、技术与发展趋势［J］.南京邮电大学学报（自然科学版），2009，29（2）：87- 94.）

［11］Wang J，Mao Y Q，Zhang H Y，et al.A new method of generating tdcs’s basis function and the analysis of its performance［J］.Journal of Air Force Engineering University（Natural Science Edition），2014，15（1）：67- 71.（王杰，毛玉泉，张衡阳，等.［J］一种新的TDCS基函数生成方法及性能分析［J］.空军工程大学学报（自然科学版），2014，15（1）：67- 71.）

［12］Xie T C，Da X Y，Chu Z Y，et al.Optimum threshold design of basis functions for transform domain communication system［J］.Systems Engineering and Electronics，2013，35（10）：2204- 2207.（谢铁城，达新宇，褚振勇，等.变换域通信系统基函数的最佳门限设计［J］.系统工程与电子技术，2013，35（10）：2204- 2207.）

［13］Mei L.Weighted-type fractional Fourier transform and its applications in communication system［D］.Harbin：Harbin Institute of Technology，2010.（梅林.加权类分数傅里叶变换及其在通信系统中的应用［D］.哈尔滨：哈尔滨工业大学，2010.）

［14］Liu S T，Zhang J D，Zhang Y.Properties of the fractionalization of a Fourier transform［J］.Optics Communications，1997，133（1／6）：50- 54.

［15］Wang J，Mao Y Q，Zhang H Y，et al.Research status and development of transform domaing communication system［J］.Telecommunication Engineering，2013，53（7）：966- 972.（王杰，毛玉泉，张衡阳，等.变换域通信系统研究现状与发展［J］.电讯技术，2013，53（7）：966- 972.）

［16］Wang S，Da X Y，Chu Z Y，et al.A new method of basis function’s pseudorandom phase generation in TDCS and its performance analysis［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2014，26（1）：37 41.（王舒，达新宇，褚振勇，等.一种新的TDCS基函数随机相位产生方法及性能分析［J］.重庆邮电大学学报（自然科学版），2014，26（1）：37- 41.）

［17］Yu B，Jia Y Q.New chaotic spread spectrum sequence and its properties analysis［J］.Electronic Technology Application，2013，39（1）：136- 142.（俞斌，贾雅琼.一种新的混沌扩频序列及其性能分析［J］.电子技术应用，2013，39（1）：136- 142.）

Method of weighted Fourier transform domain communication

DA Xin-yu，LIAN Chen
（School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China）

A new method combining the multi-terms weighted-type fractional Fourier transform（MWFRFT）and the transform domain communication system（TDCS）is put forward to improve the security of communication.Firstly，MWFRFT for sequence is used to process the original signals.Then chaos mapping is used to generate the pseudorandom phases of the basis function in TDCS.Finally，the basis function is modulated by MWFRFT signals in the covert communication.In order to show the accuracy of this method，the transformation of constellation and the correlation performance are simulated and analyzed.The result shows that MWFRFT has the diffusion and confusion property of constellation，and the new basis function has better correlation performance，so the method is suitable for covert communication.

weighted fractional fourier transform（WFRFT）；transform domain communication system（TDCS）；covert communication；spread spectrum

TN 914.42

A

10.3969／j.issn.1001-506X.2015.12.29

达新宇（1961- ），男，教授，博士，主要研究方向为信息与通信。

E-mail：daxinyu＠163.com

廉 晨（1992- ），女，硕士，主要研究方向为卫星通信、隐蔽通信。

E-mail：syclcs＠163.com

1001-506X（2015）12-2853-07

2014- 02- 09；

2015- 06- 05；网络优先出版日期：2015- 07- 28。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150728.0941.003.html

国家自然科学基金（61271250）资助课题