抗跟踪干扰的多序列跳频无线通信系统

赵 寰,全厚德,崔佩璋

(军械工程学院信息工程系,河北石家庄050003)

抗跟踪干扰的多序列跳频无线通信系统

赵 寰,全厚德,崔佩璋

(军械工程学院信息工程系,河北石家庄050003)

常规慢速频移键控跳频(frequency-hopping/frequency-shift-keying,FH/FSK)受跟踪干扰威胁严重;差分跳频抗跟踪干扰能力强,但部分频带干扰下误码率高。为提高常规慢速跳频抗跟踪干扰性能,同时不损失抗部分频带干扰性能,提出的多序列跳频(multi-sequence frequency hopping,MSFH)无线通信方式中,数据信道和补偿信道频率分别按不同跳频序列跳变,使干扰方无法准确跟踪补偿信道,减少了跟踪干扰影响;而接收机射频前端采用窄带接收,与差分跳频的宽带接收相比可有效抑制部分频带干扰。在瑞利衰落信道下,分析了卷积编码MSFH抗干扰性能。数值和仿真表明,在最坏跟踪干扰下MSFH比常规跳频约有5～10 dB误码率性能增益,且抗部分频带干扰性能优于差分跳频。

跳频;慢速;多序列跳频;跟踪干扰

0 引 言

常规慢跳速频移键控跳频(frequency-hopping/frequencyshift-keying,FH/FSK)利用载波频率的伪随机跳变可有效“躲避”部分频带干扰,但跟踪干扰下系统性能严重下降。文献[1 2]详细分析了跟踪干扰参数对干扰效果的影响。文献[3]分析了几种不同干扰策略的效果,证明最有效的策略是同时干扰数据频率及其补偿频率,且只干扰补偿频率的效果接近同时干扰两个频率,而只干扰数据频率时效果明显降低。虽然增加跳速可以有效对抗跟踪干扰,但目前大部分短波/超短波跳频仍然无法达到很高的跳速[4]。

针对慢速跳频,文献[4-7]提出基于多天线和空间分集技术的跟踪干扰消除算法,但战场等使用环境对设备移动性和小型化要求较高时,短波/超短波段多天线条件不易满足。在单天线慢速跳频条件下,文献[8]提出“非常规跳频(unconventional frequency-hopping,UFH)模式”,将FH/FSK的数据频率和补偿频率置于相互正交的信道中,并在每个信道使用未经调制的音调信号作为空中波形。文献[8]证明跟踪干扰信号会增加UFH数据信道内的信号能量,反而有利于非相干接收,可有效对抗跟踪干扰。文献[9]提出的差分跳频系统(differential frequency-hopping, DFH)同样使用这种模式,但信道选择由有用信息决定。DFH抗干扰性能近年来得到全面研究。文献[10]证明DFH具有良好的抗跟踪干扰能力。但文献[11-14]指出, DFH接收端没有信道选择的先验知识,一般采用整个工作频段上的宽带接收,且为了使编码增益最大,一般不进行窄带滤波[15],部分频带干扰下DFH误码率显著增大。特别是不考虑编码增益,仅采用逐符号译码时,DFH抗部分频带干扰性能比FH/FSK差[1617]。

为增强单天线慢跳速FH/FSK抗跟踪干扰性能,同时不损失抗部分频带干扰性能,这里建立了多序列跳频(multisequence frequency-hopping,MSFH)系统[1819]。MSFH同样使用未调制的音调信号作为空中波形,但令数据信道和补偿信道分别按照不同的跳频序列跳变,降低了跟踪干扰击中补偿信道的概率,减弱了跟踪干扰影响。另一方面, MSFH的多个跳频序列在发送端和接收端之间保持同步,因此接收机射频前端可以采用窄带接收,使MSFH仍然可以有效“躲避”部分频带干扰。MSFH可以看作对FH/FSK和DFH的折中。文献[18]考察了未编码MSFH抗白噪声性能,文献[19]得到了卷积编码MSFH抗瑞利衰落性能。

本文进一步考察瑞利衰落信道下卷积编码MSFH的抗干扰性能。首先描述了MSFH结构模型;然后在瑞利衰落信道下,得到了存在跟踪干扰时系统的误码率,分析了跟踪干扰参数对干扰效果的影响;最后简要讨论了系统抗部分频带干扰性能。数值和仿真表明,MSFH抗跟踪干扰性能优于FH/FSK,抗部分频带干扰性能优于DFH,综合抗干扰性能好。

1 系统模型

在MSFH中,整个工作频带包含WSS个正交跳频频点。发送端与接收端之间共有M个信道,一个信道在某跳内占据一个频点,此频点由信道对应的同步跳频序列决定,因此整个系统需要M个正交跳频序列。每跳在数据比特选定的一个信道上发送单音频信号,所以每跳传输的数据比特数B=log2M。

不失一般性,以二进制系统为例(B=1,M=2,以下讨论均作此假设)。如图1所示,用户数据经码率为1/Rc的二进制卷积编码,得到编码符号序列s。假设比特能量为Eb,比特持续时间为Tb,则符号能量Es=EbB/Rc,符号持续时间Ts=TbB/Rc。假设相邻频点间隔为1/Ts,跳速Th=Ts,即每跳发送1个编码符号。在t时刻,如果编码符号s=0,则使用信道0,亦即在跳频序列FS0的当前频率f(0,t)上发送单音频信号s0(t);如果编码符号s=1,则使用信道1,亦即在跳频序列FS1的当前频率f(1,t)上发送单音频信号s1(t)。其中FS0和FS1相互正交,且分别在发送端与接收端之间保持同步。最终发送信号s(t)为s0(t)与s1(t)的组合。以图1所示为例,假设符号序列s=(…,1,0,1,0,…),则相应的发送频率序列为(…,f1,f3,f2,f0,…)。发送信号的基带等效表示为

图1 MSFH发射机示意图

s(t)在射频前端经过带通滤波并上变频到发射频段进入信道。假设信道模型是频率非选择性慢衰落的,衰落幅度呈瑞利分布,在一跳之内近似为常数,且不同频点上衰落相互独立。信道内存在加性噪声和跟踪干扰。在接收端,如图2所示,第l跳的接收信号经射频前端下变频和带通滤波后,其基带等效表示为

式中,α和θ分别为等效低通信道的包络和相位,α服从参数为σα的瑞利分布,θ在[-π,π]上服从均匀分布;n(t)表示单边功率谱密度为N0的加性噪声;J(t)表示跟踪干扰。干扰方以一定成功率β跟踪数据信道的跳变,并在一跳剩余时间TJ内,在数据信道及其附近共WJ(WJ≥2)个频点上发射窄带噪声。假设延迟到下一跳内的干扰功率可忽略,干扰功率在干扰带宽上均匀分布,等效单边功率谱密度为NJ。定义平均信噪比(signal-to-noise ratio,SNR)为¯γ= 2σ2αEb/N0,等效平均信干比(signal-to-jamming ratio,SJR)为¯γJ=2σ2αEb/NJ。

图2 MSFH接收机示意图

如图2所示,在接收机内,r(t)分别与信道0和信道1的当前频率进行混频,并经中频窄带滤波后分别进行平方率非相干检测。由信道i(i=0,1)的一跳检测结果Ri得到软判决结果Y=R0-R1,然后经Viterbi译码得到原始数据。

与FH/FSK相比,MSFH不需对载波进行调制,而是靠载频本身来表示消息。对有用信号的同频干扰会使一跳信号的能量增加,这样反而会增加检测概率[10]。另一方面,不像FH/FSK和UFH中数据信道与补偿信道有固定频率间隔,MSFH的数据信道和补偿信道频率间隔是伪随机的,即使干扰方截获了数据信道频率,也难以估计补偿信道频率,因此MSFH补偿信道被有效干扰的概率降低。如图3所示,跟踪干扰以一定的带宽即可干扰FH/FSK全部4跳中的补偿信道,而MSFH第2跳和第4跳中补偿信道没有被干扰。根据文献[3],不能有效干扰补偿信道将使干扰效果弱化。

图3 跟踪干扰对MSFH和FH/FSK影响的比较

考虑MSFH抗部分频带干扰性能。与DFH相比,MSFH数据信道和补偿信道被同步跳频序列严格约束,因此其合法频率转移路径远少于DFH,可以更好地抑制部分频带干扰。如图4所示,第4跳f2上的干扰可直接被MSFH的窄带接收机滤除,而在相同信道条件下,干扰进入DFH宽带接收机。假设DFH译码网格如图4所示,其中实线所示为正确的频率转移路径。在第4跳,虽然f2不在第3跳正确接收频率的扇出路径上,但同样有可能造成译码错误:若因f2上干扰的影响,第4跳接收到的频率被判决为f2,则按照序列译码规则,图4所示正确路径和错误路径的译码度量相同。在以后的译码过程中,这条错误路径可能会幸存下来,并最终造成第3跳和第4跳译码都发生错误。而且注意到这种错误不能通过在DFH译码前增加窄带滤波来避免,因为DFH正是利用宽带接收来更新每条路径的度量,从而实现最大似然译码的,窄带滤波会使带外频点上的度量丢失[15]。

需要注意的是,MSFH要求收发双方在使用的所有序列上均取得同步。为保持同步信号与数据信号的特征一致,采用自同步法。对M个序列的同步捕获检测值进行合并,再用合并值进行同步识别,使合成序列达到同步,进而使对应的每个跳频序列分别完成同步,代价是比传统跳频系统所需的同步时间稍长。以下讨论时均假设已取得严格同步。

图4 部分频带干扰对MSFH和DFH影响的比较

2 误码率分析

本节首先得到跟踪干扰下的系统误码率,再进行简单修正得到部分频带干扰下的误码率。

2.1 跟踪干扰下MSFH误码率

不失一般性,假设用户数据为全0序列,则编码后亦为全0序列。在第l跳,考虑信道i(i=0,1)的检测结果Ri受干扰情况。用随机变量qi=1或0表示Ri被干扰或不被干扰,则在信道i的非相干检测器处,干扰和噪声的功率谱密度可统一表示为

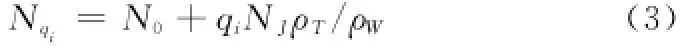
式中,ρT=TJ/Th,表示一跳内被干扰时间占一跳时间的比例;ρW=WJ/WSS,表示干扰带宽占总跳频带宽的比例。

软判决结果Y=R0-R1的干扰状态与Ri的干扰状态有关,因此令随机变量Qj=(q0q1)表示Y的干扰状态,其中j=0,1,2,3。Qj与q0,q1的关系如表1所示。假设两信道的干扰状态相互独立,则Qj的概率分布为

表1_一跳干扰状态Qj与各信道干扰状态qi的关系

当发送编码符号为s(s=0或1),干扰状态为Qj时,判决结果Y的概率密度函数为判决结果Y送入译码器进行Viterbi译码,找出一条似然概率最大的路径作为译码输出。用pY(y|s)表示编码符号为s时Y的似然函数。为简化计算,使用对数似然函数ln pY(y|s)作为译码度量,则Viterbi算法等价于找到一条累积译码度量最大的路径。其比特误码率Pb的联合上界[20]可表示为式中,dfree表示卷积码的最小自由距离;ak为与正确路径首次汇合且距离为k的路径上的错误比特数,这两个参数由卷积码的生成函数确定;P2(k)为成对错误概率,即一条与正确路径距离为k的错误路径被选为幸存路径的概率。因为已假设发送全0序列,则成对错误概率为

式中,r遍历错误路径与正确路径不同的k个符号。假设这k个符号中,第r个符号对应判决结果yr干扰状态为Qrj,令Q=(Q1j,…,Qrj,…,Qkj)表示所有k个符号对应判决结果的干扰状态向量,且在Q中,干扰状态Qj发生的次数分别为kj,k0+k1+k2+k3=k。从而可将式(10)化为条件成对错误概率P2(k,Q)的平均,即

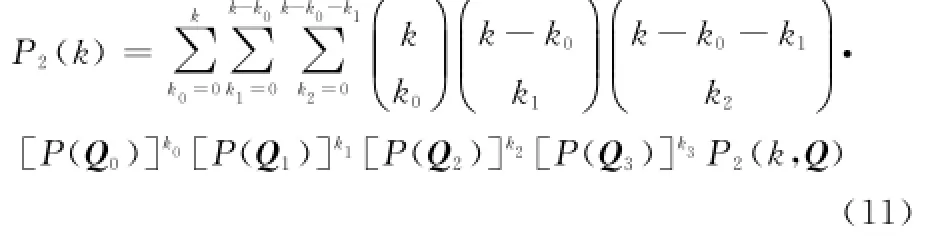
式中,P2(k,Q)可表示为

由式(8)知,式(12)中pY(yrj|s,Qj)(s=0,1)是分段函数,分段点在y=0。因此进一步假设在每种干扰状态Qj对应的kj个判决结果Yj中,有nj个大于0(用Y+j表示),其余(kj-nj)个小于0(用Y-j表示)。并令向量N=(n0,n1,n2, n3),则可再次将P2(k,Q)看作P2(k,Q,N)的平均,即

式中

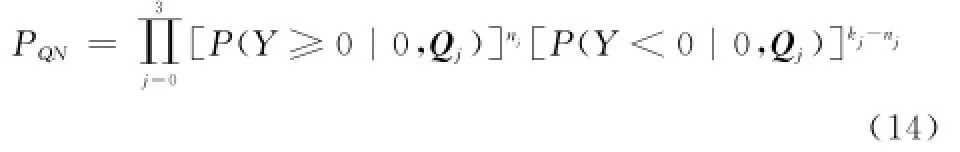
式中,P(Y≥0|0,Qj)和P(Y＜0|0,Qj)分别是发送符号s=0,干扰状态为Qj时Y≥0和Y＜0的概率,可由式(8)中Y的概率密度函数在相应的区间上积分得到。而式(13)中条件成对错误概率P2(k,Q,N)可表示为则可得U的分布函数

式中,D2=D3+D4。特殊地,当D3=0,D4＞0时,B0n=0; B1n=0(当n＜D4)或B1n=1(当n=D4)。当D4=0,D3＞0时,B1n=0;B0n=0(当n＜D3)或B0n=1(当n=D3)。

因此,式(15)可化为

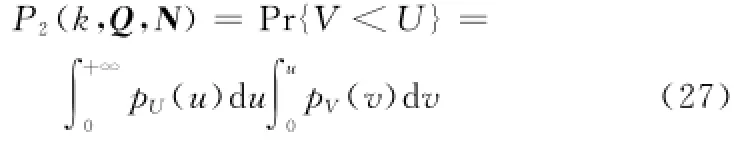
将式(22)、式(24)代入式(27)并积分,可得

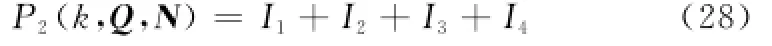
式中

特殊地,当n1=n2=n3=n4=0时,P2(k,Q,N)= Pr{U＞0}=∫+∞0pU(u)d u=1。当k1-n1=k2-n2=k3-n3=k4-n4=0时,P2(k,Q,N)=Pr{V＜0}=0。

至此,可由式(28)得到P2(k,Q,N),将其代入式(13)得到P2(k,Q),进而代入式(11)可得到成对错误概率P2(k),最后将P2(k)代入式(9)即可得到跟踪干扰下MSFH的比特误码率上限。

2.2 部分频带干扰下MSFH误码率

部分频带干扰可以看作跟踪干扰的一种特殊情况,即干扰方无法准确跟踪数据信道,而只能随机选择干扰频带的位置,相当于跟踪成功率下降到β=ρW=WJ/WSS。因此,在部分频带干扰下,可得Qj的概率分布为

将式(33)～式(36)代入式(11),即可计算成对错误概率P2(k),同理,将P2(k)代入式(9)即可得到部分频带干扰下MSFH的比特误码率上限。

3 仿真与数值分析

不失一般性,假设跳频带宽内有32个跳频频点, MSFH使用码率为1/2的卷积编码,最小自由距离dfree=5时的一个生成多项式为[(5)8(7)8][20]。令平均信噪比¯γ为16.7 d B,此时MSFH在无干扰瑞利衰落信道下的比特误码率约为10-5。

图5比较了跟踪干扰和部分频带干扰下MSFH误码率仿真值和数值计算得到的上限。仿真结果与数值计算结果基本重合,说明第2节得到的误码率上限是非常紧密的。图5中,跟踪干扰和部分频带干扰带宽相同(同为ρW= 0.25),但跟踪干扰条件下系统误码率明显高于部分频带干扰条件。这是因为跟踪干扰成功率很高(β=1),相应地,在跟踪干扰下状态Q3发生的概率高于部分频带干扰条件下。而根据文献[3],在4种干扰状态中Q3导致的误码最严重。

图5 跟踪干扰/部分频带干扰下MSFH误码率仿真与数值对比(ρW=0.25,跟踪干扰β=1,ρT=1)

MSFH抗跟踪干扰性能与常规二进制FH/FSK(FH/ BFSK)进行比较。假设两者跳频带宽相同,FH/BFSK中数据频率与补偿频率的间隔固定为1/Ts,且采用与MSFH同样的卷积编码和软判决Viterbi译码。跟踪干扰方跟踪数据信道的跳变,并在数据信道及其附近频点上发射窄带噪声。这样,对FH/BFSK来说,成功的跟踪干扰总是同时覆盖数据频率和补偿频率。与文献[2]相似,观察跟踪干扰的时间比例ρT、成功率β和带宽比例ρW对干扰效果的影响,结果分别如图6～图8所示。

图6 跟踪干扰ρT对MSFH与常规FH/BFSK误码率影响(ρW=1/8,β=1)

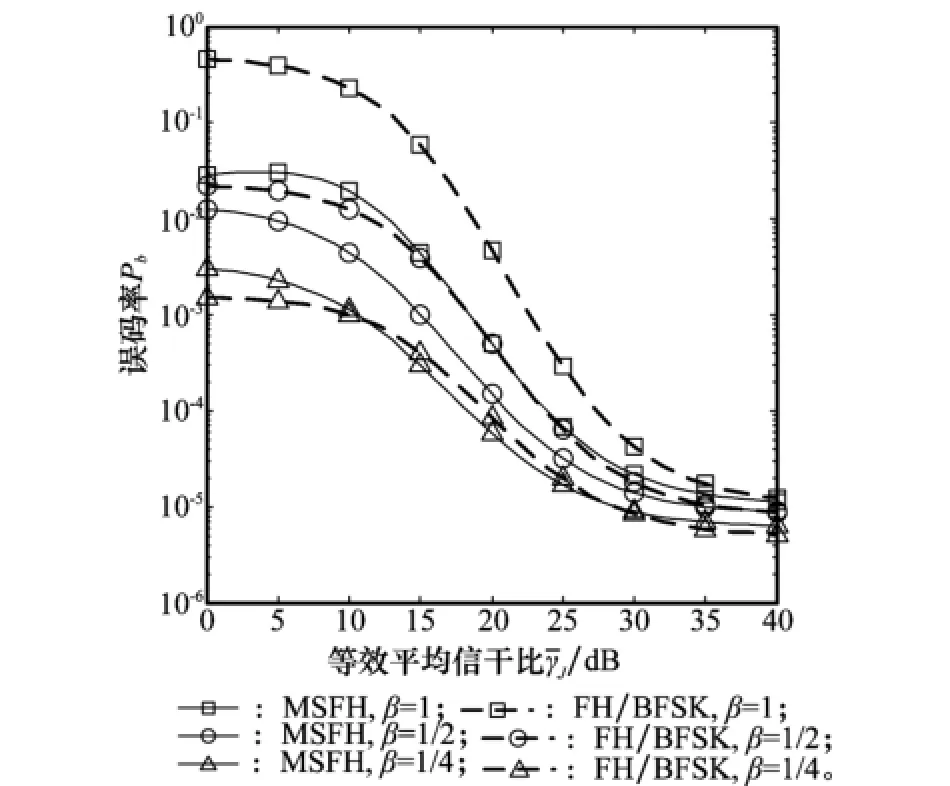
图7 跟踪干扰β对MSFH与常规FH/BFSK误码率影响(ρW=1/8,ρT=1)

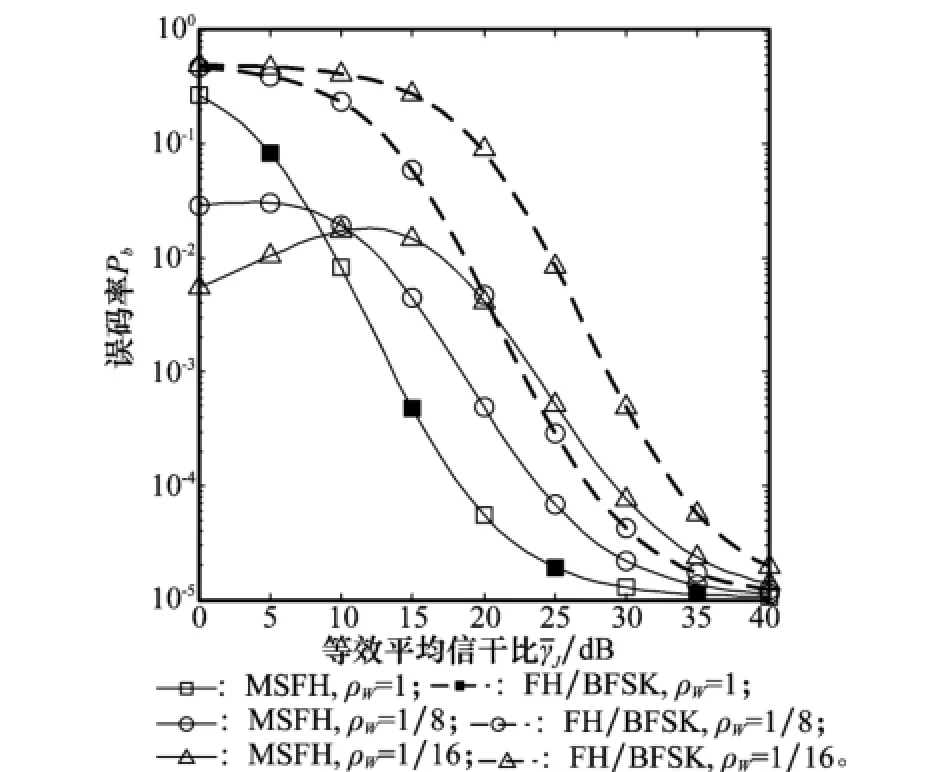
图8 跟踪干扰ρW对MSFH与常规FH/BFSK误码率影响(β=1,ρT=1)

跟踪干扰时间比例ρT对MSFH与FH/BFSK误码率的影响如图6所示。两者的误码率都随ρT的增大而增大。对相同ρT,中等信干比下MSFH比FH/BFSK普遍约有3～5 dB性能增益;而在小信干比下MSFH性能增益更大,可达5 dB以上。

干扰成功率β对干扰效果的影响如图7所示。MSFH与FH/BFSK误码率都随β的增大而增大;当β较大时, MSFH比FH/BFSK普遍约有3～5 dB性能增益;而在小信干比下,MSFH性能增益可达5 d B以上。可见MSFH通过降低补偿信道被干扰的概率,带来的抗跟踪干扰性能增益是明显的。由图7亦可发现,当干扰成功率接近干扰带宽比例(图中β=1/4,ρW=1/8),即跟踪干扰逐渐退化为部分频带干扰时,MSFH相比FH/BFSK的误码率性能优势不明显。这一点将在图9部分频带干扰条件下进一步说明。

图8所示为跟踪干扰带宽比例ρW对干扰效果的影响,条件为干扰成功率β=1,干扰时间比例ρT=1。此时ρW使系统误码率达到最大的跟踪干扰称为最坏跟踪干扰。图8中当ρW=1,即宽带干扰时,MSFH与FH/BFSK误码率重合。随ρW减小,FH/BFSK误码率增大,即FH/BFSK的最坏跟踪干扰带宽很窄。而ρW与MSFH误码率之间的关系有所不同:在大信干比和中等信干比(约¯γJ＞10 dB)下, MSFH误码率随ρW增大而减小,即最坏跟踪干扰是窄带的;而随信干比降低,MSFH最坏跟踪干扰的带宽急剧变宽,最后变为宽带干扰。在最坏跟踪干扰下,MSFH比FH/BFSK普遍约有5～10 d B性能增益。值得注意的是,当跟踪干扰带宽很窄(ρW=1/16)时,MSFH误码率先随信干比减小而增大,达到最大值后,随信干比继续减小,MSFH误码率反而逐渐减小。这是因为跟踪干扰带宽特别窄时,击中补偿信道的概率很小,而数据信道上干扰信号功率很大,此时将增大数据信道的非相干接收能量,有利于正确判决。图6～图8显示MSFH抗跟踪干扰能力明显优于FH/BFSK。

图9比较了MSFH,FH/BFSK和DFH的抗部分频带干扰性能。其中FH/BFSK模型与图6～图8中相同。而DFH工作带宽亦分为32个频点,扇出系数为2,采用线性合并译码[21]方法。这种情况下DFH的G函数可等效为dfree=5的卷积编码,编码增益与MSFH和FH/BFSK相同。由图9可见,在相同干扰带宽下,MSFH误码率远低于DFH。这是因为MSFH采用窄带接收,相比DFH的宽带接收,进入接收机的干扰较少。而在小信干比下,MSFH比FH/BFSK误码率略高,这是因为较强的部分频带干扰仅击中MSFH补偿信道时,将使MSFH产生非常严重的误码。虽然在图9中没有画出,但实际上当ρW取小于1的其他值时,以上结论仍然成立。图9显示MSFH抗部分频带干扰能力明显优于DFH。

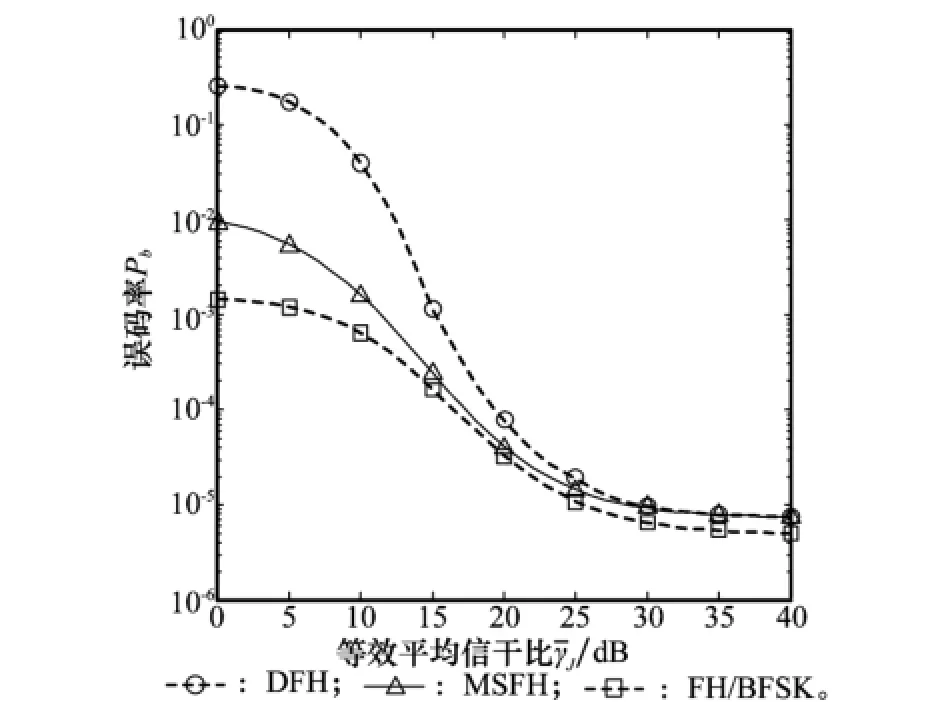
图9 部分频带干扰对MSFH、DFH和FH/BFSK误码率影响(ρW=1/8)

4 结 论

本文提出的MSFH中,数据信道和补偿信道频率分别按各自的跳频序列跳变,增加了传输频率的随机性,提高了抗跟踪干扰性能;同时窄带接收保证了良好的抗部分频带干扰性能。在频率非选择性瑞利慢衰落信道下,详细分析了跟踪干扰对系统误码率的影响,并简要讨论了系统抗部分频带干扰性能。结果表明,MSFH抗跟踪干扰性能优于FH/FSK,而抗部分频带干扰性能优于DFH。虽然以慢速跳频为例,但MSFH亦适用于快速跳频。

[1]Felstead E B.Follower jammer considerations for frequency hopped spread spectrum[C]∥Proc.of the IEEE Military Communications Conference,1998:474-478.

[2]Lee C,Jeong U,Ryoo J Y,et al.Performance of follower noise jammers considering practical tracking parameters[C]∥Proc.of the 64th IEEE Vehicular Technology Conference,2006:1 5.

[3]Poisel R A.Modern communications jamming principles and techniques[M].2nd ed.Norwood:Artech House,2006:167-170.

[4]Ko C C,Nguyen-Le H,Huang L.ML-based follower jamming rejection in slow FH/MFSK systems with an antenna array[J]. IEEE Trans.on Communications,2008,56(9):1536-1544.

[5]Eken F.Use of antenna nulling with frequency-hopping against the follower jammer[J].IEEE Trans.on Antennas and Propagation,1991,39(9):1391-1397.

[6]Liu F,Nguyen-Le H,Ko C C.Vector similarity-based detection scheme for multi-antenna FH/MFSK systems in the presence of follower jamming[J].IET Signal Processing,2008,2(4): 346-353.

[7]Wang Y,Wu G.Covariance-based follower jamming blocking algorithm for slow FH-BFSK systems[C]∥Proc.of the Asian-Pacific Con ference on Communications,2009:148-152.

[8]Hassan A A,Stark W E,Hershey J E.Error rate for optimal follower tone-jamming[J].IEEE Trans.on Communications, 1996,44(5):546-548.

[9]Herrick D L,Lee P K.CHESSa new reliable high speed HF radio[C]∥Proc.of the IEEE Military Communications Conference,1996:684-690.

[10]Mills D G,Edelson G S.CHESS study final report[R].New York:DARPA and AWL,2001.

[11]Zhu Y C,Gan L C,Lin J,et al.Performance of differential frequency hopping systems in a fading channel with partial-band noise jamming[C]∥Proc.of the International Conference on Wireless Communications,Networking and Mobile Computing, 2006:1-4.

[12]Zhu Y C,Gan L C,Xiong J Q,et al.Performance analysis of shortwave differential frequency hopping systems with partialband jamming[J].Chinese Journal of Radio Science,2006,21 (6):885 890.(朱毅超,甘良才,熊俊俏,等.短波差分跳频系统抗部分频带干扰性能分析[J].电波科学学报,2006,21 (6):885-890.)

[13]Lou J Y,Qu X X,Wang S.Error probabilities of differential frequency hopping receiver with noise-normalization combining sequence detection under partial-band jamming[C]∥Proc.of the International Conference on Wireless Communications and Signal Processing,2010:1-4.

[14]Qu X X,Wang S,Lou J Y.Performance analysis of NNC-DFH receiver over Nakagami fading channel with partial-band jamming[J].Journal of Electronics&Information Technology, 2011,33(7):1544-1548.(屈晓旭,王殊,娄景艺.Nakagami衰落信道下NNC-DFH接收机抗部分频带干扰性能分析[J].电子与信息学报,2011,33(7):1544-1548.)

[15]Dong B H.Performance analysis of an improved differential frequency hopping communication system[D].Chengdu:University of Electronic Science and Technology of China,2010.(董彬虹.改进差分跳频通信系统性能分析[D].成都:电子科技大学,2010.)

[16]Pan W,Zhou S D,Yao Y.Performance analysis of differential frequency hopping communication system[J].Acta Electronica Sinica,1999,27(11A):102-104.(潘武,周世东,姚彦.差分跳频通信系统性能分析[J].电子学报,1999,27(11A):102-104.)

[17]Qu X X,Wang S,Lou J Y,et al.Performance analysis of antijamming of partial-band in NNC-DFH receivers[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(9):1-5.(屈晓旭,王殊,娄景艺,等.NNC-DFH接收机抗部分频带干扰性能分析[J].华中科技大学学报(自然科学版),2011,39(9):1-5.)

[18]Zhao H,Quan H D,Cui P Z.Multi-sequence frequency hopping system and its performance over AWGN channel[J].Journal of Signal Processing,2013,29(5):600-606.(赵寰,全厚德,崔佩璋.多序列跳频系统及其在AWGN信道下误码率性能分析[J].信号处理,2013,29(5):600-606.)

[19]Zhao H,Quan H D,Cui P Z.Multi-sequence frequency hopping system and its performance over Rayleigh fading channel[J].Journal of Signal Processing,2013,29(8):1077 1083.(赵寰,全厚德,崔佩璋.多序列跳频系统及其在瑞利衰落信道下性能分析[J].信号处理,2013,29(8):1077-1083.)

[20]Proakis J G.Digital Communications[M].4th ed.New York: Mc Graw-Hill,2001:338-349.

[21]Chen Z,Li S Q,Dong B H,et al.Synchronous multi-user performance of differential frequency hopping over Rayleigh fading channels[J].Journal of University of Electronic Science and Technology of China,2008,37(2)206-209.(陈智,李少谦,董彬虹,等.瑞利衰落信道下差分跳频同步多用户性能[J].电子科技大学学报,2008,37(2)206-209.)

全厚德(1963-

赵 寰(1985-),男,教授,博士,主要研究方向为无线通信系统抗干扰。

E-mail:zkjysyyb@163.com

崔佩璋(1974-),男,副教授,博士,主要研究方向为无线通信系统抗干扰。

E-mail:cpz_zk@163.com

Follower-jamming resistible multi-sequence frequency hopping wireless communication

ZHAO Huan,QUAN Hou-de,CUI Pei-zhang
(Information Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,China)

The conventional slow-hopping-rate frequency-hopping/frequency-shift-keying(FH/FSK)is threatened by follower jamming(FJ).On the other hand,the differential frequency hopping(DFH)can resist FJ efficiently,but its bit error rate rises significantly under partial band jamming(PBJ).To enhance the FJ rejection capability of the slow-hopping-rate FH/FSK without the expense of PBJ rejection capability,the proposed multi-sequence frequency hopping(MSFH)mode makes the data channel and the complementary channel hop on their respective frequency sequences,which will lure the follower jammer out of aiming at the complementary channel,thus mitigating the effect of FJ.Besides,the narrow-band front end is employed in the MSFH receiver,which will resist PBJ more efficiently than the wide-band receiver of DFH.In the Rayleigh fading channel,the anti-jamming performance of the convolutional coded MSFH is evaluated.Numerical and simulation results show that,the MSFH generally outperforms FH/FSK by 5～10 dB when under the worst-case FJ, and also outperforms DFH notably when under PBJ.

frequency-hopping(FH);slow-hopping-rate;multi-sequence frequency-hopping(MSFH);follower jamming(FJ)

TN 914.4

A

10.3969/j.issn.1001-506X.2015.03.31

),男,博士研究生,主要研究方向为短波无线通信抗干扰技术。

E-mail:zhaohuan_mec@163.com

网址:www.sys-ele.com

1001-506X(2015)03-0671-08

2014 05 29;

2014 07 07;网络优先出版日期:2014 09 28。

网络优先出版地址:http:∥w ww.cnki.net/kcms/detail/11.2422.TN.20140928.1610.008.html

总装备部军内科研基金资助课题