多传感器网络目标检测方法综述
2015-06-05闫永胜王海燕申晓红
闫永胜,王海燕,张 秀,申晓红
(西北工业大学航海学院,陕西西安710072)
多传感器网络目标检测方法综述
闫永胜,王海燕,张 秀,申晓红
(西北工业大学航海学院,陕西西安710072)
在并行拓扑结构下,从系统级的角度对多传感器网络目标检测方法进行综述,将似然比检测归纳分类为统计量(决策统计量和融合统计量)的确定和门限(决策门限和融合门限)的求解两部分,并分别展开论述。在硬决策融合系统统计量确定方面,分别归纳了理想信道、非理想信道条件下,不同融合统计量构成检测器的检测性能优劣,并通过仿真试验对比分析了不同融合统计量的检测性能;在软决策融合系统统计量确定方面,归纳了软决策融合系统中局部传感器节点性能度量方式,并对比分析了局部传感器节点决策空间划分方法;在门限求解方面,将门限求解方法归纳总结为逼近法、迭代法、蒙特卡罗方法,并分析比较这些方法的适用范围、优缺点等;最后,对多传感器网络目标检测进行了展望。
信号与信息处理;多传感器网络;决策融合;目标检测;综述
0 引 言
随着微机电系统、无线通信技术和大规模集成电路技术的发展,低功耗、低成本、多用途传感器的研制成为可能,进而孕育出许多新的信息感知和处理模式,多传感器网络(multi-sensor network,MSN),即分布式传感器网络,就是其中一例。MSN是由小型、低功耗的节点组成,且节点之间通过无线或有线连接方式形成自组织网络,通过MSN中节点的信息融合,可以显著提高系统的感知和处理增益[-13]。在民用领域,MSN常用于环境监测、灾难预警[46]及健康护理[7]等;在军事领域,MSN常用于目标检测、定位、跟踪[810]、战场态势评估等。
具有信息融合能力MSN目标检测兴起于20世纪80~90年代。在分布式雷达对目标检测过程中,数据传输的高成本促使设计者在传输信息之前压缩数据,从而引申出MSN目标检测概念。文献[11]率先将传统的检测理论扩展到MSN目标检测中,研究了两个传感器的分布式检测问题。近年来,随着MSN技术的发展,涌现出一些综述文献[1215]。文献[12]总结了无线传感器网络(一种特殊的MSN)下分布式决策融合方法,并提出了进一步推动分布式决策融合从理论进入工程应用领域的展望,该文献仅仅对衰落信道条件下融合中心融合统计量进行综述,而没有从MSN目标检测系统级的角度对融合检测问题进行探讨;文献[13-15]在分析了水声信道特点基础上,对大规模MSN进行了综述,重点从水声通信角度出发阐述了各个协议层所面临的挑战,并强调了跨层设计方法在优化水声MSN设计中的重要价值。这些综述文献从不同角度对MSN技术进行梳理,但是对协同信号处理方法尤其是目标检测的共性问题缺乏深入的剖析。
本文总结了当前MSN决策融合目标检测方面的主要成果,依据阈值检测方法将MSN决策规则归纳分类为统计量的确定和门限的求解,并从这两个角度对MSN决策方法及其构成系统的性能进行综述。
1 MSN目标检测拓扑结构及框架
从MSN网络拓扑结构划分,可将MSN目标检测系统分为:串行、并行和树形,以及带有反馈的串行、带有反馈的并行等[16-19]。当MSN中传感器节点数目有限时,相比于无反馈检测系统,反馈可以提高检测系统的检测性能[16];当MSN中传感器节点数目较大时,对于二元假设检验问题,反馈并不能够显著提高检测系统的检测性能[20],且局部传感器判决规则、融合规则求解运算复杂度高,不适用于实时性要求高的检测系统。串行MSN目标检测系统最大缺点在于任意一条通信连接中断或任意一个传感器节点失效都会导致整个检测系统瘫痪;树形MSN目标检测系统也存在类似串行MSN目标检测系统的隐患。而并行MSN目标检测系统则不然,由于各个传感器节点工作相互独立,一个或几个传感器节点失效不影响其他节点工作。即使在并行MSN机构中融合中心节点起着中央枢纽的作用,但是在简单的控制机制下,其他传感器节点可以在突发情况下成为融合中心节点。因此,本文重点针对并行MSN目标检测系统展开综述。
具有并行拓扑结构的MSN目标检测系统如图1所示,该系统由局部传感器节点(local sensor nodes,LSN)、传输信道、数据融合中心(data fusion center,DFC)组成。分布在监测区域的LSN采集监测区域信息xi,并依据LSN判决规则ui=γi(xi)输出局部判决结果,当ui∈{0,1}时,融合系统称为硬决策融合系统,当ui∈{0,1,…,M-1}时,融合系统称为软决策融合系统。这些结果调制后经信道传输至DFC,DFC对接收到的数据y=[y1,y2,…,yN]T,采用融合规则u0=γ0(y)确定最终的输出u0∈{H0,H1},其中,H0表示无目标,H1表示有目标。整个数据传递过程可以分为三层:局部判决层、信道传输层、数据融合层,分别对应局部传感器判决规则、信道传输模型、融合规则。文献[21]论证了在并行融合拓扑结构中二元假设检验背景下,LSN的最优判决规则和DFC的最优融合规则均是似然比检测。似然比检测是一种阈值检测,因此可以从统计量的确定和门限的求解两部分对MSN目标检测系统进行综述。

图1 并行拓扑结构的MSN目标检测
2 检测统计量的确定
当MSN采用硬决策融合时,LSN的检测性能(检测概率和虚警概率)在一定程度上表征了LSN判决规则的优劣,但是在分析MSN目标检测系统性能时,可以通过假设LSN检测性能已知,重点考虑DFC融合统计量;当MSN采用软决策融合时,与硬决策融合系统相反,主要考虑LSN判决规则,即LSN观测空间的划分方法,而DFC融合规则可以参照硬决策融合系统DFC融合规则。因此,本文在检测统计量确定方面重点分析硬决策融合系统的DFC融合统计量以及软决策融合系统的LSN观测空间划分方法。
2.1 硬决策融合系统的DFC融合统计量
依据LSN与DFC之间传输信道类型,DFC融合统计量可分为:①理想信道DFC融合统计量;②非理想信道DFC融合统计量。理想信道DFC融合统计量适合于有线传感器网络,在确定融合统计量过程中,不考虑信息在信道传输过程中的传输错误;非理想信道DFC融合统计量的表达式与信道建模方式有关,从信道建模方法可将非理想信道DFC融合统计量确定方法分为两类:①衰落信道建模融合统计量确定;②传输错误概率建模融合统计量确定。
2.1.1 理想信道DFC融合统计量
当LSN向DFC传输ui∈{1,0}数据时,假设传输信道是理想的,且传感器间观测相互独立,则DFC最优融合统计量为似然比融合统计量,可表示为

依据DFC融合统计量所需先验信息多少,可将似然比融合统计量归纳为Chair-Varshney统计量、GLRT统计量、Bayes统计量以及Counting统计量。
(1)Chair-Varshney统计量
Chair和Varshney推导了似然比检测统计量,提出了一种DFC最优融合规则[22],其融合统计量为

式中,pdi(xt,yt)和pfa分别是LSN的检测概率和虚警概率,pdi(xt,yt)是目标位置(xt,yt)的函数。由式(2)可以看出,Chair-Varshney融合统计量是LSN判决结果ui的加权,加权因子是各个LSN的判决性能参数。该统计量建立在目标位置已知的基础上,实际中,目标位置是未知的,因此,该融合统计量常用来作为硬决策融合统计量的性能上限,其他的融合统计量与其相比较。
(2)GLRT统计量
文献[23]提出了广义似然比检测(generalized likelihood ratio test,GLRT)统计量,其表达式为GLRT统计量求解分为两步:①采用最大似然估计

(max likelihood estimation,MLE),最大化H1条件下对数似然函数

求解位置参数的估计^θ=(^xt,^yt);②依据式(3)计算GLRT融合统计量Λ2。GLRT统计量是对目标的联合定位、检测,但是先估计目标位置,再进行目标检测不符合实际应用中的信号处理顺序,违背了目标检测的意义。
(3)Bayes统计量
鉴于GLRT统计量实际意义较小以及GLRT统计量中MLE运算量大的缺点,文献[24]从Bayes角度出发,通过引入目标位置的先验分布,对似然函数积分,以消除统计量中未知的目标位置信息,提出了一种Bayes融合统计量,该统计量表达式为

式中,f(xt,yt)=为目标位置的先验分布,式中积分是通过数值二重积分实现的。
(4)Counting统计量
以上的统计量Λ1,Λ2,Λ3都是建立在LSN判决性能参数(pdi和pfa)已知的基础上,但是在实际的目标检测应用中,LSN的某次判决性能参数很难确定,即使这些判决性能参数可以确定,但是传输这些参数到DFC也是需要很大代价的,因此文献[25-26]提出了一种Counting融合统计量:

该融合统计量不需要LSN的先验知识,仅依据DFC接收到的局部判决结果进行累加得到DFC的融合统计量,当LSN数目很大时,Counting统计量构建的融合规则是渐进最优融合规则[25-26]。此外,在Counting统计量的基础上,文献[27-28]给出了一种用于融合系统给的扫描统计量(scan statistic,SS),该统计量是Counting统计量的改进,其将传感器覆盖区域划分为较小的窗体,每个窗体内部计算LSNs输出1的个数,这些窗体中1的个数最大值即为SS统计量。SS统计量适用于大规模MSN条件下主动目标探测,当节点数目较大时,其性能优于Counting统计量,但是SS统计量要求MSN布放时在每个滑动窗体内部,传感器节点数目大致相同,这种要求大大增大了MSN布放成本,在一定程度上违背了大规模MSN的初衷。

表1 不同理想信道条件下DFC融合统计量比较
(5)不同统计量比较
表1总结了理想信道条件下DFC融合统计量,分别从统计量需求的先验知识、特点、运算量、DFC检测性能分析采用方法以及难易程度等5个角度进行对比,其中检测性能分析所采用的方法将在后续展开论述。此外,通过蒙特卡罗仿真试验来对比不同融合统计量构成目标检测系统的检测性能,仿真模型及仿真条件如下。

仿真模型:式中,si是接收LSNs采集到的数据;ai是信号幅度,满足ai=是二维坐标系下第i个LSN距目标(xt,yt)的距离,ni~N(0,σ2)。该模型下,第i个LSN的虚警概率和检测概率分别为
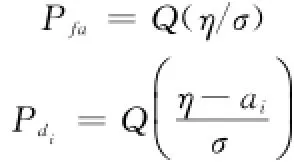
式中,η为第i个LSN的判决门限;Q(·)是标准正态分布随机变量的右尾概率,定义为
仿真条件:目标在d0处以P0=5 000各向同性地向外辐射能量,假设目标位于二维平面(15,36)处,能量是以球面扩展方式衰减的;N=20个LSNs均匀分布在200 m× 200 m区域内检测目标的有无。LSN虚警概率Pfa=0.1,融合中心虚警概率PFA=0.01;蒙特卡罗次数M=104次。图2给出了Chair-Varshney、Bayes、GLRT以及Counting统计量的ROC曲线。

图2 理想信道条件下不同融合规则ROC曲线性能对比
从图2可以看出,Chair-Varshney统计量的检测性能最优,其完全利用了目标的位置信息,GLRT统计量和Bayes统计量的性能相当,优于Counting统计量。GLRT统计量的检测性能很大程度上取决于MLE目标位置的估计,而精确的目标位置估计需要较多的传感器节点数目,故本文选取传感器节点数为N=20,经过100次Monte Carlo MLE试验得到目标位置的估计结果为(20.6,46.7)。
2.1.2 非理想信道DFC融合统计量
为了寻求更加切合实际的基于MSN目标检测方法,文献[29-31]将瑞利衰落信道模型与决策融合相结合,在获取一定信道先验知识条件下,得到了似然比融合统计量;文献[32-35]采取信道衰落最终的表现形式——平均错误概率这一不同建模方式,并结合MSN目标检测系统,分析了最优或次优DFC融合统计量。
(1)衰落信道建模DFC融合统计量
衰落信道建模从传输层角度出发,忽略传输过程中的载波、相干解调步骤,建立衰落信道下数据的传输模型,如图3所示。
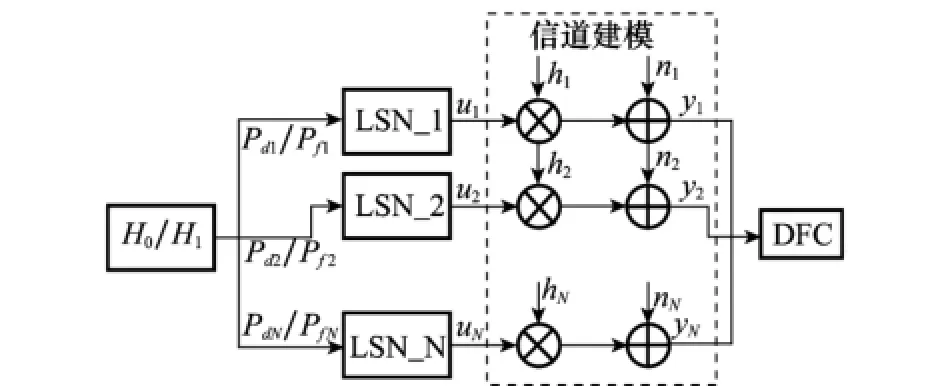
图3 衰落信道条件下并行拓扑结构MSN决策融合模型
假设第i个LSN发送的数据ui∈{+1,-1}经过衰落信道输出为yi=hiui+ni,其中hi为衰落信号包络,其概率密度函数为f(hi)=2hie-hi2,hi≥0,ni为均值为0方差为σ2的高斯随机过程。最优融合统计量为似然比检测统计量:

基于似然比检测统计量在理论上可以证明其检测性能是最优的,但是DFC需要完整的信道信息hi。一般采用信道估计方法来获取,但这种方法需要消耗大量的能量资源。因此通过寻求一些不需要完全获取信道信息的融合统计量,以达到节约整个探测系统能量的目的。
①衰落信道下Chair-Varshney融合统计量
衰落信道下Chair-Varshnety融合统计量是一种次优的统计量[31],具体表达式为

文献[29]证明了Chair-Varshney融合统计量是高通信信噪比条件下最优似然比检测统计量的逼近,并通过仿真试验验证了在低通信信噪比(SNR=10log)条件下该统计量构成的检测系统存在较大的性能损失。
②MRC融合统计量
MRC融合统计量是一种次优的统计量,同时也需要DFC获取信道的全部信息,具体的表达式为

MRC融合统计量是低通信信噪比条件下最优似然比检测统计量的逼近,但是在高通信信噪比条件下该统计量构成的检测系统存在较大性能损失[29]。衰落信道下融合统计量ΛC_1和ΛC_2可以从另外一个角度解释:高通信信噪比下,LSN传输的数据可以被DFC可靠接收,因此融合统计量与信道信息无关;低通信信噪比下,衰落信道对融合统计量的影响最为严重。
③EGC融合统计量
一种由理想信道条件下Counting融合统计量启发得来了融合统计量[30],成为EGC融合统计量:

该融合统计量表达式简单,仅需要将DFC所得结果累加求和即可,已有结果表明EGC算法在较宽的通信信噪比范围内,检测性能良好,鲁棒性强。
④基于信道统计特性的LRT融合统计量(LRT_CS)
Chair-Varshney,MRC,EGC融合统计量建立在连续信道状态信息hi的基础上,实时获取hi是不切实际的。因此,文献[31]构建了一种基于传输信道统计特性的LRT融合统计量:
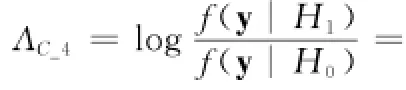

文献[31]通过仿真试验表明,这种LRT_CS融合统计量建立在慢变衰落信道基础上,不需要连续的信道状态信息。
⑤基于信道估计的LRT融合统计量
文献[37]对通信信道处理采用了不同的方法,假设LSN与DFC之间信道是慢衰落瑞利信道,在发送判决结果之前,发送已知的训练字符,通过最小均方误差估计信道冲击响应,进而分析研究这种构架的决策融合系统检测性能,其融合统计量在BPSK调制方式下表达式为~h+σ2n是系统等效噪声,由信道估计误差和信道加性高斯白噪声组成,通信信噪比SNR=B/σ2n,h^n是通过训练确定的信道估计。

融合统计量ΛC_5给出了衰落信道条件下Chair-Varshney融合统计量ΛC_1、MRC融合统计量ΛC_2和EGC融合统计量ΛC_3的一种实现方法,即通过在传输判决信息之前发送训练字符,获得信道的估计。
⑥不同LRT决策融合统计量比较
表2总结了非理想信道条件下不同的LRT融合统计量,分别从所需信道的先验知识、统计量特点以及检测性能优劣等角度进行对比。
其中,li∈{±B}是发送的训练字符;σ2w=Bσ2

表2 衰落信道条件下不同LRT决策融合统计量比较
这些次优的融合统计量均是独立随机变量的和,因此可通过中心极限定理(center limit theorem,CLT)逼近正态分布的方法,来评估目标检测系统的检测性能,仿真模型及仿真条件如下。
仿真模型:假设LSNs检测性能已知,分析不同融合统计量的检测性能。通过求取式(7)~式(10)在H0、H1假设下的均值和方差,获取DFC闭式的检测概率和虚警概率表达式。
仿真条件:传感器节点数目N=6,LSN虚警概率Pfa= 0.1,假设LSNs的检测概率相同Pd=0.6,信道服从单位能量的瑞利衰落,即f(hi)=2hie-h2i,平均比特信噪比SNR= 10 dB。CLT逼近得到的ROC曲线如图4所示,可以看出,随着虚警概率的增加,DFC检测概率增大,并趋向于1; LRT_CS统计量检测性能优于其他3种统计量。
(2)平均传输错误概率建模DFC融合统计量
从概率角度出发,一种描述LSN与DFC之间通信信道的方法是定义二进制对称信道(binary symmetric channel,BSC)的平均错误概率P(yi|ui),在二进制数字调制系统中,其是一个交叉概率[34];在多进制数字调制系统中,其是一个平均错误概率转移矩阵。这种依据传输错误概率进行信道建模的方法,不必假设信道具体实现形式,有效地克服了衰落信道建模方法在某些情况下的局限性,普适应强。

图4 衰落信道条件下不同融合统计量ROC曲线性能对比(CLT逼近)
在这种建模下,没有形成较为系统的分类,不同科研工作者在不同条件下给出了最优或次优的融合统计量。传输错误概率假设概率转移矩阵MDy×Du,其第ij个元素为
Mij=P(yl=i|ul=j),i=1,…,Dy;j=1,…,Du(12)
概率转移矩阵影响融合统计量,进而影响目标检测系统检测性能。文献[34]在采用传输错误概率方法对信道建模的基础上,分别给出了Bayes准则、Neyman-Pearson(N-P)准则下DFC检测性能的渐进错误指数,并在Bayes准则下给出了融合统计量表达式,即DFC对接收到的各个LSN数据进行求和,但非理想信道导致的传输错误概率影响了DFC门限的求解;文献[32]采用传输错误概率建模方法分析了给定LSN决策规则时,两个传感器节点在“AND”、“OR”、“XOR”融合规则下的检测性能,推导了传输错误概率建模下LSN的检测规则,并将这种信道建模方法推广应用到多个传感器决策融合中;文献[38-40]在信道传输错误概率建模的基础上,研究了LSN多比特量化的决策融合算法。
这些文献在平均错误概率建模的基础上,获得了不同形式的融合统计量,并分析了检测系统的检测性能。与衰落信道建模方法相比,这种信道建模方法可以将信道的衰落特性、信号调制方式以及噪声干扰反映到平均错误概率中。
(3)两种信道建模方法的关系
针对LSN与DFC之间不同的信道建模方式,DFC的融合统计量表征也不同。衰落信道建模方式最终输出形式即为平均错误概率,衰落信道建模方式可以通过衰落信道上的单信道接收性能分析方法来转化为平均错误概率建模,具体方法如下。
在衰落信道中,接收信号功率随空间和时间随机变化,因此,平均差错率也是随机变化的,用平均差错率Pb( E)来表示衰落信道的误码特性[41],可表示为



LSN向DFC传输n bits判决信息,则平均传输错误k bits信息的概率为

作为一种特例,当平均传输错误概率应用于硬决策融合系统时,传输1 bit局部传感器判决信息错误1 bit的平均概率为

因此,由衰落信道模型(16)可以推导得到平均传输错误概率表达式如式(18)、式(19)所示,此外,式(16)的衰落信道模型未考虑信号的调制方式,而平均传输错误概率建模方式可以将不同的调制方式(BPSK,FSK)反映到错误概率中,进而最终反映到DFC的融合统计量中。
2.2 软决策融合系统的LSN判决统计量
软决策融合系统的特点是每个LSN向融合中心传输的数据是对观测空间的多级量化结果,一般而言,软决策融合系统的检测性能优于硬决策融合系统的检测性能[4243]。
2.2.1 软决策融合系统中LSN的性能度量方式
软决策融合系统中LSN的判决性能参数与硬决策融合系统中LSN的判决性能参数表达方法不同,硬决策融合系统中,可以依据LSN的输出ui∈{0,1}来判决目标的有无,此时存在N-P准则下的检测概率以及Bayes准则下的最小错误概率。但在软决策融合系统中,LSN输出的是多比特量化信息,不存在像硬决策融合系统中的检测概率或虚警概率,因此需要寻求LSN的性能度量方式。
软决策融合系统,可以通过概率向量对(αjk,βjk)之间的距离来评测,其中αjk=P(uj=k|H0),βjk=P(uj=k|H1), k∈{0,1,…,M},M=2L是量化级数,L是量化位数。从信息论角度出发,K-L距离、Vairational距离、Chernoff信息在一定程度上反映出DFC对LSN概率向量对的分辨力[44],分别表示如下:
Kullback-Leibler距离[45- 46]:
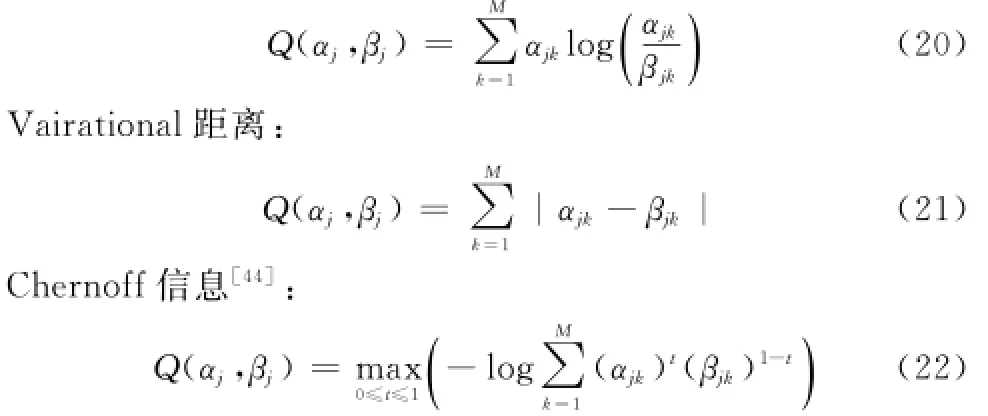
其中,Kullback-Leibler距离和Chernoff信息分别是N-P准则和Bayes准则下的渐近误差指数[47]。以上的LSN性能度量方式一个重要作用是在大量的LSN中选取有效的节点参与软决策融合,以通过这样的节点选择方式降低整个系统的能量消耗。
2.2.2 软决策融合系统LSN量化方法
软决策融合系统中获取最优的LSN观测空间划分规则是异常复杂的[38,4849],尤其是当传感器节点间观测相关情况下[50]。这种运算复杂度高的LSN最优量化规则对于实时的目标探测系统而言是不可能实现的,因此学者致力于寻求次优或便于计算的观测空间划分方法,本文将软决策系统观测空间划分法归纳分类为:最优决策空间划分方法、检测统计量均分观测空间划分方法、概率均分观测空间划分方法。
(1)最优决策观测空间划分法
文献[51]在硬决策空间划分基础上,提出了N-P准则下决策空间划分的最优方法:对LSN的硬决策空间再划分,对判决为H0的决策空间Ω0和判决为H1的决策空间Ω1再划分,但是在求解最优划分概率时,很难得到解析解,且计算复杂度随着节点数目增加成指数增长。在此基础上,提出了采用最大化J散度准则求解最优的虚警概率和检测概率划分法,旨在强调LSN对DFC的信息量贡献。
(2)检测统计量均分法
相明等人在文献[52-53]提出了一种检测统计量均分方法,并在融合中心采用随机化检测方法,分析了采用该均分法构建的软决策融合系统的检测性能。
检测统计量均分法原理[54]:当检测统计量li(zi)>Ti存在一个值Ai,使得P(li(zi)>Ai|H0)≈0,则为了充分反映ui=1的可信度,仅需对区间[Ti,Ai]进行量化。同理,显然存在一个值Bi,使得P(li(zi)<Bi|H1)≈0,为了充分反映ui=0的可信度,仅需对区间[Bi,Ti]进行量化,将[Ti,Ai]均匀划分为2m个区间,对应的门限分别为T11, T12,…,T12m-1,并从左至右标上序号0,…,2m-1,序号即为其可信度。同理对区间[Bi,Ti]均匀划分为2m个区间,对应的门限分别为T01,T02,…,T02m-1,并依次标为0,…, 2m-1来反映其可信度。当m=2时,对传感器观测空间划分如图5所示。

图5 当量化级数为4级时,传感器观测空间再划分方法
将检测统计量——LSN观测值的似然比进行等间距划分[43],LSN输出取决于似然比检测统计量与检测门限之间的差值,在N-P准则下,该软决策融合系统的检测性能分析表明:随着量化级数的增加,软决策融合系统的检测性能逼近集中式系统的检测性能,高于硬决策融合系统检测性能。
(3)概率均分法
文献[55]提出了一种基于概率均分法的决策空间划分方法,其实质是将整个观测空间Ωi划分为两个互不相交的部分ΩiH0和ΩiH1。然后按照检测概率对空间ΩiH1再划分为2m个互不相交的空间,满足要求

依次标上序号0,…,2m-1,序号即为其可信度。按照虚警概率对空间ΩiH0
再划分为2m个互不相交的空间,满足要求

图6给出了当量化为2级情况下,传感器观测空间划分方法。
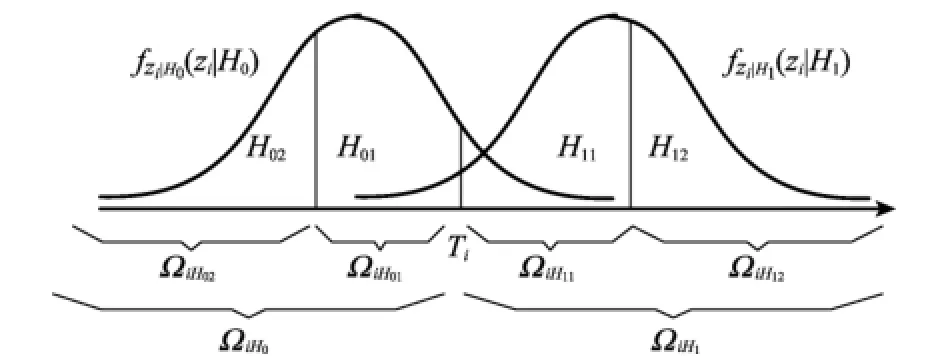
图6 当量化级数2级时,传感器观测空间再划分方法
基于检测统计量均分的观测空间划分法在融合中心求解融合规则时,需要求解大量LSN的虚警概率和检测概率,基于概率均分的决策空间划分法简化了LSN的计算量[55]。
(4)其他决策空间划分方法
最优决策空间划分、检测统计量均分以及概率均分法以外,存在其他的一些决策空间划分法。文献[56 57]在认知无线电频谱感知应用中,通过分布式检测来确定某种频谱的有无,在决策空间划分方面,划分为4级,中间级门限λ采用硬决策融合系统的判决门限,其他级门限分别为λ±x,λ±x±y,其中,门限间隔x和y通过最小化DFC的量化误差来决定。区别于硬决策融合系统中LSN的阶跃式判决输出结果,文献[58-59]将LSN观测值yi,0≤i≤N映射到连续递增的置信隶属度函数μi(yi)∈[0~1]上,并依据最小均方量化误差准则得到量化结果(即Lloyd-Max量化器)。结果表明这种LSN观测空间划分方法构成的检测系统检测性能明显优于硬决策系统的检测性能。
(5)不同软决策空间划分方法对比
为了避免最优决策空间划分的复杂性求解,学者们提出了检测统计量均分法和概率均分法,两者简化了决策空间划分过程。检测统计量均分法是一种直观的表述,其在计算概率(αjk,βjk)并传输这些数据到DFC是一个较为复杂过程;概率均分法是分别对H1决策空间和H0空间的等概率再划分,当LSN判决规则确定后,不必求解概率向量对,简化了LSN的运算量,相比检测统计量均分法,概率均分法运算复杂度更低。在检测性能方面,这两种决策空间划分方法并未给出优劣,这一点可作为后续的一个研究分支。
3 检测门限求解及检测器性能评估
为了得到DFC融合规则的检测性能或者在N-P准则下求解检测门限,需要确定离散融合统计量的概率分布或概率分布列(这里将这种方法称为直接法),但是,这一离散随机变量的概率分布列或连续随机变量的概率分布一般未知或很难得到解析解,或者虽然概率分布列或概率分布已知,但是依据概率分布直接计算检测性能所需付出较大的代价。当探测系统节点数目较大时,运算复杂度成指数增加。因此,学者们寻求易于计算的门限求解方法及检测性能评估方法,本文归纳总结为以下几种方法:逼近法、迭代法、蒙特卡罗方法等。逼近法是通过概率论知识近似得出融合统计量的概率分布列或概率分布,从而确定检测门限及获取检测器性能评估。逼近法分为常规逼近和鞍点逼近[60];N-P准则下的迭代法主要是指给定虚警概率,通过循环迭代方法求解LSN和DFC的检测门限,主要有:穷举法、K-L距离迭代法[61]、粒子滤波迭代法等。
3.1 逼近法
3.1.1常规逼近
由于DFC融合统计量具有式(1)的形式,可以看作是独立随机变量的和,因此在仅获得随机变量的一阶矩和二阶矩情况下,采用CLT进行正态逼近,即当节点数目N→+∞时,检测统计量在Hi(i=0,1)条件下的概率密度服从高斯分布,利用此逼近求解N-P准则下融合门限,进而评估检测器性能,该方法即为常规逼近,也称作CLT逼近。
常规逼近可以解决很多实际问题,文献[29,62]采用常规逼近方法评估检测器检测性能,但是该方法建立在大规模传感器探测系统的基础上,当节点数目较小时,逼近精度较差,尤其是当要逼近的概率位于密度函数尾部区域时,这一结论在一定程度上说明了常规逼近法的局限性。
3.1.2鞍点逼近
对于独立随机变量之和,鞍点逼近是逼近概率密度函数或者尾概率密度函数最有效的方法[60,63]之一。在常规逼近中应用中心极限定理逼近融合统计量的尾概率分布误差较大的主要原因是待估计值,即融合统计量融合门限与真实的融合统计量概率密度函数均值相差较远,在这种情况下,鞍点逼近方法将融合统计量真实的概率密度函数通过指数偏移实现均值偏移,从而构建出新的概率密度函数,使其均值逼近待估计值(融合统计量融合门限),进而采用常规逼近方法得到融合统计量的概率密度函数。鞍点逼近未知的概率密度函数所采用的指数偏移方法表达式为fs^,i(x,^θi)=ex^θi-Ki(θ^i)fs,i(x)(23)式中,^s是偏移后的随机变量;fs,i(x)=fs(x|Hi)表示s在假设Hi的概率密度函数;Ki(θ)是s的累积生成函数,对于MSN目标检测问题而言Ki(θ)=N log(E(eθl|Hi))。
文献[63]通过仿真试验验证了随着WSN规模增大,逼近真实尾概率的相对误差迅速减小,并保持在O(N-1)或O(N-3/2)数量级。在运算复杂度方面,鞍点逼近方法在确定构建逼近概率密度函数的参数^θ时,采用Newton-Raphson算法计算,需要M+1次加法、M+3次乘法、3次除法和M次求幂操作(M为LSN的量化级数),该运算复杂度远小于直接计算概率密度函数所需的O(NM-1)数量级。
3.2 迭代法
迭代法主要通过搜索方式确定DFC融合门限,进而进行MSN目标检测系统的性能评估。将迭代法归纳分类为穷举迭代法、在线学习迭代法以及粒子滤波迭代法,这些迭代法的本质是搜索合适的门限以达到一定准则下的最优。
3.2.1 穷举迭代法
穷举迭代法的核心思想是:DFC在确定融合门限过程中,通过排列各个LSN输出组合,利用N-P准则下离散融合统计量随机化检测必要性[6465]的特点,搜索得出DFC融合统计量的融合门限,进而确定MSN目标检测系统的检测性能。文献[52,66]基于穷举迭代法搜索确定了DFC融合门限,并采用随机化检测方法求解随机化因子,进而确定MSN目标检测系统的检测性能。
穷举迭代法在确定门限过程中,运算复杂度为O(N2b-1)数量级(N为传感器节点数目,b为每个LSN量化输出位数,M=2b为量化级数),随着MSN目标检测系统节点数目增加,迭代法搜索的次数指数增加,因此该方法只适合于MSN小规模的目标检测系统(传感器节点数目少)。
3.2.2 在线学习迭代法
在线学习迭代法的核心思想是:最小化观测数据与所需输出分布之间的Kullback-Leibler距离(K-L距离),K-L距离表达式为

从而达到在线搜索门限的目的,并采用牛顿迭代法或Gauss-Seidel迭代法等优化求解K-L距离的最小值。该方法直接对获取的数据或LSN判决输出进行操作,不需要精确的获取LSN判决统计量、DFC融合统计量的概率分布。
文献[61]就是基于此思想给出了一种门限在线学习方法,利用K-L距离函数严格的凸性,虚警概率p是门限λ的函数p=p(λ),α是N-P准则下要达到的虚警概率,当且仅当p=α时,K-L距离达到全局最小值,在一些通用假设条件下,估计的门限值λ以1概率收敛于真实门限值。为了增加迭代速度,采用牛顿迭代法求解函数∂K(α,p)/∂λ=0的解,以加快虚警概率p向α收敛的速度。
在线学习迭代法不需要获取H1和H0假设下概率分布的先验知识,仅依靠接收到的观测数据,即可迭代求取门限值。但是,在搜索门限时,需要构造N-P准则下虚警概率与门限的函数p(λ),构造过程复杂,且在迭代过程中,需要满足一定条件以达到迭代收敛的目的。
3.2.3 粒子滤波迭代法
统计优化思想亦可应用在最优门限求解过程,文献[67]提出了一种基于粒子滤波的门限迭代求解方法。DFC应用最小错误概率准则进行最优传感器门限迭代搜索,通过粒子滤波算法迭代确定代价函数的局部最小值,比较这些局部最小值,以获得全局最小值,进而确定该最小值所对应的粒子——LSN检测门限。
粒子滤波迭代法不需要建立在已知H1,H0概率密度函数已知的假设下,仅需要假设初始粒子在一定范围内服从均匀分布。文献[67]在最小错误概率准则下通过对粒子进行重采样迭代获取最小化错误概率所对应的LSN判决门限。该方法和在线学习迭代法相同,不需要假设概率密度函数,且对初始值的选取要求不高,但是迭代求解过程复杂,同样不适于实时的MSN目标探测系统。此外,为了避免搜索到错误概率的局部最小值,需要多次选取不同的初始值,迭代得到不同的错误概率,通过比较选择最终的最小错误概率对应的门限。
3.3 蒙特卡罗仿真方法
当H0和H1条件下的概率密度函数很难解析地确定,且不满足逼近条件或逼近效果不理想时,可以采用蒙特卡罗仿真分析法求解给定虚警概率条件下的检测门限,进而进行检测性能分析。在检测性能评估方面,该方法有效地避免了许多复杂运算。但是,为了得到估计精度,需要产生的从而使得求解的概率具有100(1-α)%的置信度,其中P是被估计概率,ε=|^P-P|/P为相对误差。

3.4 不同门限求解方法比较
表3给出了门限求解方法或检测性能评估方法的优缺点与计算复杂度的对比。不同方法适用不同的应用背景:常规逼近适合于待逼近点(融合统计量门限)在真实融合统计量概率密度函数均值周围的情况;鞍点逼近适合逼近独立随机变量和的分布;迭代法中穷举法适合于较小规模MSN目标检测系统的门限求解,其他迭代法没有特定的限制,但是运算量较大。需要说明的是:虽然在线学习迭代法和粒子滤波方法中运算复杂度表达式一致,但是实际运算量不同,M×K×N是指迭代次数,不同方法基本操作不同,运算时间不同;蒙特卡罗仿真方法是一种较为简便的门限确定方法,经常用于融合统计量构成检测器的性能评估,但是需要大量的实验次数。样本数目应该足够大,且满足条件[68]

表3 门限求解、性能评估方法比较
4 结束语
本文对基于MSN的目标检测方法进行综述,将检测问题归纳划分为统计量的确定和门限的求解两个方面。在硬决策融合系统统计量确定方面,重点讨论数据融合中心融合统计量的求解,并依据LSN与DFC之间信道建模的有无,将硬决策融合系统中融合统计量的确定方法归纳分类为理想信道条件下融合统计量的确定、非理想信道条件下融合统计量的确定两部分。在此基础上,对比分析了不同条件下融合统计量确定方法的优缺点。在软决策融合系统统计量确定方面,重点论述了LSN的观测空间划分法;在门限确定方面,将门限确定方法归纳划分为逼近法(常规逼近和鞍点逼近)、迭代搜索法(穷举法、在线学习迭代法、粒子滤波法)、蒙特卡罗仿真方法,并分析对比了不同方法的优缺点。
随着传感器网络相关技术的发展,在多MSN目标检测方面,仍然存在着挑战,还有一些亟待解决的问题,可以从以下几个方面开展工作:
(1)非理想信道条件下,自适应门限求解问题
目前大多数研究者在利用自适应求解检测问题门限过程中,往往建立在理想通信信道的假设上,如何利用在线学习等算法自适应地求解检测门限(LSN判决门限和DFC融合门限),从而满足一定准则下的最优是未来MSN目标检测的研究重点之一。
(2)非理想信道条件下,多目标函数优化问题
在无线传感器网络通信信道中,尤其是水声传感器网络通信信道中,衡量一个检测系统是否最优不仅仅由检测性能(检测概率、贝叶斯风险、K-L距离等)决定,还包括系统内部通信量、检测系统消耗能量、局部传感器节点和数据融合中心的运算复杂度等因素。这种情况下,基于MSN目标检测系统最优就演化为一个多目标函数优化问题。
(3)特定应用背景下的MSN目标检测问题
水声传感器网络目标检测:传统的MSN目标检测方法没有考虑传感器与融合中心之间的共享信道特点,这一特性对于水声传感器网络目标检测而言,更为严峻。这是因为水声信道具有传输衰减大、多径衰落严重、通信带宽有限、噪声谱级高等特点[6972]。因此,水声传感器网络背景下的目标检测应用中,如何对多径强、传播时延长、衰落水声信道建模,如何在通信带宽有限、传感器节点能量有限情况下寻求一种最优或次优的融合规则有待于进一步研究。
小规模MSN目标检测系统建模:小规模MSN具有节点数目少的特点,MSN目标检测融合方法在求解门限时,对于离散的融合统计量不能直接求解其概率分布列,当通过逼近方法逼近其概率分布列时,由于不满足逼近条件,结果逼近误差较大,因此节点数目较少情况下目标检测是一个亟待解决问题。
[1]Akyildiz I F,Su W,Sankarasubramaniam Y,et al.Wireless sensor networks:a survey[J].Computer Networks,2002,38 (4):393-422.
[2]Gharavi H,Kumar S P.Scanning the issue:special issue on sensor networks and applications[J].Proceedings of the IEEE, 2003,91(8):1151-1153.
[3]Bal M,Shen W,Ghenniwa H.Collaborative signal and information processing in wireless sensor networks:a review[C]∥Proc. of the IEEE International Conference on Systems,Man and Cybernetics,2009:3240-3254.
[4]Yu T C,Lin CC,Chen C C,et al.Wireless sensor networks for indoor air quality monitoring[J].Medical Engineering&Physics,2013,35(2):231-235.
[5]Chen D,Liu Z,Wang L,et al.Natural disaster monitoring with wireless sensor networks:a case study of data-intensive applications upon low-cost scalable systems[J].Mobile Networks and Applications,2013,18(5):651-663.
[6]Bouabdellah K,Noureddine H,Larbi S.Using wireless sensor networks for reliable forest fires detection[J].Procedia Computer Science,2013,19(1):794 801.
[7]Rezaee A A,Yaghmaee M H,Rahmani A M,et al.HOCA: healthcare aware optimized congestion avoidance and control protocol for wireless sensor networks[J].Journal of Network and Computer Applications,2014,37(1):216 228.
[8]Cohen K,Leshem A.Performance analysis of likelihood-based multiple access for detection over fading channels[J].IEEE Trans.on Information Theory,2013,59(4):2471-2481.
[9]Wang G,Li Y,Ansari N.A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J]. IEEE Trans.on Vehicular Technology,2013,62(2):853 -862.
[10]Vempaty A,Han Y,Varshney P.Target localization in wireless sensor networks using error correcting codes[J].IEEE Trans.on Information Theory,2014,60(1):697-712.
[11]Tenney R R,Sandell N R.Detection with distributed sensors[J]. IEEE Trans.on Aerospace and Electronic Systems,1981,17(1): 501-510.
[12]Yang X J.Review of distributed decision fusion in wireless sensor networks[J].Computer Engineering and Applications, 2012,48(11):1-6.(杨小军.无线传感器网络下分布式决策融合方法综述[J].计算机工程与应用,2012,48(11):1-6.)
[13]Akyildiz I F,Pompili D,Melodia T.Challenges for efficient communication in underwater acoustic sensor networks[J]. ACM Sigbed Review,2004,1(2):3-8.
[14]Akyildiz I F,Pompili D,Melodia T.Underwater acoustic sensor networks:research challenges[J].Ad Hoc Networks,2005, 3(3):257-279.
[15]Heidemann J,Ye W,Wills J,et al.Research challenges and applications for underwater sensor networking[C]∥Proc.of the IEEE Wireless Communications and Networking Conference,2006:228-235.
[16]Alhakeem S,Varshney P K.Decentralized Bayesian detection with feedback[J].IEEE Trans.on Systems,Man and Cybernetics—Part A:Systemsand Humans,1996,26(4):503-513.
[17]Tay W P,Tsitsiklis J N,Win M Z.On the subexponential decay of detection error probabilities in long tandems[J].IEEE Trans.on Information Theory,2008,54(10):4767-4771.
[18]Tay W P,Tsitsiklis J N,Win M Z.Data fusion trees for detection:does architecture matte[J].IEEE Trans.on Information Theory,2008,54(9):4155-4168.
[19]Tay W P,Tsitsiklis J N,Win M Z.Bayesian detection in bounded height tree networks[J].IEEE Trans.on Signal Processing,2009,57(10):4042-4051.
[20]Tay W P.The value of feedback in decentralized detection[J]. IEEE Trans.on Information Theory,2012,58(12):7226 -7239.
[21]Ahmadi H R,Vosoughi A.Distributed detection with adaptive topology and nonideal communication channels[J].IEEE Trans.on Signal Processing,2011,59(6):2857 2874.
[22]Chair Z,Varshney P K.Optimal data fusion in multiple sensor detection systems[J].IEEE Trans.on Aerospace and Electronic Systems,1986,(1):98 101.
[23]Niu R,Varshney P K.Joint detection and localization in sensor networks based on local decisions[C]∥Proc.of the Fortith IEEE Conference on Signals,Systems and Computerson, 2006:525-529.
[24]Guerriero M,Svensson L,Willett P.Bayesian data fusion fordistributed target detection in sensor networks[J].IEEE Trans.on Signal Processing,2010,58(6):3417-3421.
[25]Niu R,Varshney P K,Cheng Q.Distributed detection in a large wireless sensor network[J].Information Fusion,2006,7 (4):380-394.
[26]Niu R,Varshney P K.Performance analysis of distributed detection in a random sensor field[J].IEEE Trans.on Signal Processing,2008,56(1):339-349.
[27]Guerriero M,Willett P,Glaz J.Distributed target detection in sensor networks using scan statistics[J].IEEE Trans.on Signal Processing,2009,57(7):2629-2639.
[28]Song X,Willett P,Glaz J,et al.Active detection with a barrier sensor network using a scan statistic[J].IEEE Journal of Oceanic Engineering,2012,37(1):66-74.
[29]Chen B,Jiang R,Kasetkasem T,et al.Channel aware decision fusion in wireless sensor networks[J].IEEE Trans.on Signal Processing,2004,52(12):3454-3458.
[30]Chen B,Jiang R,Kasetkasem T,et al.Fusion of decisions transmitted over fading channels in wireless sensor networks[C]∥Proc. of the IEEE Conference on Signals,Systems and Computers, 2002:1184-1188.
[31]Niu R,Chen B,Varshney P K.Fusion of decisions transmitted over Rayleigh fading channels in wireless sensor networks[J]. IEEE Trans.on Signal Processing,2006,54(3):1018 1027.
[32]Xia Y,Wang F,Deng W S.The decision fusion in the wireless network with possible transmission errors[J].Information Sciences,2012,199:193-203.
[33]Chen B,Willett P K.On the optimality of the likelihood-ratio test for local sensor decision rules in the presence of nonidealchannels[J].IEEE Trans.on Information Theory,2005,51 (2):693-699.
[34]Cheng Q,Chen B,Varshney P K.Detection performance limits for distributed sensor networks in the presence of nonideal channels[J].IEEE Trans.on Wireless Communications,2006, 5(11):3034-3038.
[35]Chen H,Chen B,Varshney P K.Further results on the optimality of the likelihood-ratio test for local sensor decision rules in the presence of non-ideal channels[J].IEEE Trans.on Information Theory,2009,55(2):828-832.
[36]Li Y J,Wang Z,Sun Y X.Decision fusion under fading channel in resource-constrained wireless sensor networks[J].Journal of Software,2007,18(5):1130-1137.(李燕君,王智,孙优贤.资源受限的无线传感器网络基于衰减信道的决策融合[J].软件学报, 2007,18(5):1130-1137.)
[37]Xu Z H,Huang J G,Zhang L L,et al.System modeling and performance analysis for detection fusion of multiple arrays under low SNR[J].Systems Engineering and Electronics,2011, 33(11):2418 2422.(徐振华,黄建国,张玲玲,等.低信噪比条件下多基阵检测融合系统建模与性能分析[J].系统工程与电子技术,2011,33(11):2418 2422.)
[38]Liu B,Chen B.Channel-optimized quantizers for decentralized detection in sensor networks[J].IEEE Trans.on Information Theory,2006,52(7):3349-3358.
[39]Liu Y L,Feng X X,Dang H G,et al.The fusion algorithm of soft decision in distributed detection based on non-ideal channel[J]. Journal of Air Force Engineering University(Natural Science E-dition),2008,9(2):44-47.(刘英坤,冯新喜,党宏刚,等.基于非理想信道的分布式多检测器软决策融合算法[J].空军工程大学学报(自然科学版),2008,9(2):44 47.)
[40]Cheng V W,Wang T Y.Performance analysis of distributed decision fusion using a multilevel censoring scheme in wireless sensor networks[J].IEEE Trans.on Vehicular Technology, 2012,61(4):1610-1619.
[41]Proakis J.Digital communicutions[M].5th ed.New York: McGraw Hill,2008:160-220,846-850.
[42]Shorey R,Ananda A,Chan M C,et al.Mobile,wireless,and sensor networks:technology,applications,and future directions[M].Hoboken:Wiley,2006.
[43]Aziz A M.A simpleand efficient suboptimal multilevel quantization approach in geographically distributed sensor systems[J].Signal Processing,2008,88(7):1698-1714.
[44]Fabeck G,Bielefeld D,Mathar R.Cross-layer resource allocation in sensor networks for distributed detection with soft decision fusion[C]∥Proc.of the IEEE Second International Workshop on Cross Layer Design,2009:1-5.
[45]Xiao JJ,Luo Z Q.Universal decentralized detection in a bandwidth-constrained sensor network[J].IEEE Trans.on Signal Processing,2005,53(8):2617-2624.
[46]Yang Y,Blum R S,Sadler B M.A distributed and energy-efficient framework for Neyman-Pearson detection of fluctuating signals in large-scale sensor networks[J].IEEE Journal on Selected Areas in Communications,2010,28(7):1149-1158.
[47]Thomas J A.Elements of information theory[M].Hoboken:Wiley,2006.
[48]Viswanathan R,Varshney P K.Distributed detection with multiple sensors I.fundamentals[J].Proceedings of the IEEE, 1997,85(1):54-63.
[49]Gustafsson F,Karlsson R.Statistical results for system identification based on quantized observations[J].Automatica,2009, 45(12):2794-2801.
[50]Helstrom C W.Gradient algorithm for quantization levels in distributed detection systems[J].IEEE Trans.on Aerospace and Electronic Systems,1995,31(1):390-398.
[51]Lee C C,Chao J J.Optimum local decision space partitioning for distributed detection[J].IEEE Trans.on Aerospace and Electronic Systems,1989,25(4):536-544.
[52]Xiang M,Wang Z,Li H,et al.A fusion algorithm for distributed underwater signal detection[J].Journal of Northwestern Polytechnical University,2000,18(2):237-240.(相明,王昭,李宏,等.一种分布式水声信号检测系统的融合算法[J],西北工业大学学报,2000,18(2):237 240.)
[53]Bai Y S,Zhao J W,Xiang M,et al.The distributed detection fusion on narrowband underwater acoustic signal[J].Journal of System Simulation,2003,15(7):931-938.(白银生,赵俊渭,相明,等.窄带水声信号的分布式检测融合[J].系统仿真学报, 2003,15(7):931-938.)
[54]LüG F,Wang H Y,Shen X H,et al.Performance analysis of different quantitative rules about soft decision system on non-ideal channel[J].Electronic Design Engineering,2013,21(7): 51- 54.(吕国飞,王海燕,申晓红,等.非理想信道不同量化规则软决策算法性能分析[J].电子设计工程,2013,21(7):51 -54.)
[55]Xia S Z,Zhou W X.Soft decision fusion algorithm for distributed detection[J].Chinese Journal of Sensors and Actuators, 2008,21(7):1164- 1168.(夏双志,周万幸.分布式检测系统的一种软决策融合算法[J].传感技术学报,2008,21(7):1164 -1168.)
[56]Van Den Biggelaar O,Dricot J M,De Doncker P,et al. Quantization and transmission of the energy measures for cooperative spectrum sensing[C]∥Proc.of the 71st IEEE Vehicular Technology Conference,2010:1 5.
[57]Mustonen M,Matinmikko M,Mammela A.Cooperative spectrum sensing using quantized soft decision combining[C]∥Proc.of the 4th IEEE International Conference on Cognitive Radio Oriented Wireless Networks and Communications,2009:1- 5.
[58]Aziz A M.A soft-decision fusion approach for multiple-sensor distributed binary detection systems[J].IEEE Trans.on Aerospace and Electronic Systems,2011,47(3):2208 2216.
[59]Aziz A M.A new adaptive decentralized soft decision combining rule for distributed sensor systems with data fusion[J].Information Sciences,2014,256:197- 210.
[60]Aldosari S A.Detection in sensor networks[D].Pennsylvania: Carnegie Mellon University,2005.
[61]Pados D A,Papantoni-Kazakos P,Kazakos D,et al.On-line threshold learning for Neyman-Pearson distributed detection[J]. IEEE Trans.on Systems,Man and Cybernetics,1994,24(10): 1519- 1531.
[62]Sestok C K,Said M R,Oppenheim A V.Randomized data selection in detection with applications to distributed signal processing[J].Proceedings of the IEEE,2003,91(8):1184 -1198.
[63]Aldosari S A,Moura J M F.Detection in sensor networks:the saddlepoint approximation[J].IEEE Trans.on Signal Processing,2007,55(1):327- 340.
[64]Willet P,Warren D.The suboptimaliy of randomized tests in distributed and quantized detection systems[J].IEEE Trans.on Information Theory,1992,38(2):355- 361.
[65]Xiang M,Zhao J.On the performance of distributed Neyman-Pearson detection systems[J].IEEE Trans.on Systems,Man and Cybernetics—Part A:Systemsand Humans,2001,31(1):78- 83.
[66]Xiang M,Wang Z,Li Hong,et al.Study on the performance of datafusion system for underwater signal detection[J].Acta Acoustic,1999,24(6):574-581.(相明,王昭,李宏,等.水声信号数据融合系统的性能研究[J].声学学报,1999,24(6):574 -581.)
[67]Kyriakides I,Cochran D.Threshold optimization for distributed detection using particle filtering methods[C]∥Proc.of the IEEE Workshop on Sensor Array and Multichannel Processing,2006:481-485.
[68]Kay S M.Fundamentalsof statistical signal processing:detection theory[M].Prentice Hall PTR,1998:36-40
[69]Shen X H,Wang H Y,Zhao B Z,et al.A more secure underwater acoustic frequency hopping communication system based on chaotic sequence[J].Journal of Northwestern Polytechnical University,2006,24(2):180 184.(申晓红,王海燕,赵宝珍,等.基于混沌序列的水声跳频通信系统研究[J].西北工业大学学报,2006,24(2):180-184.)
[70]Qarabaqi P,Stojanovic M.Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels[J].IEEE Journal of Oceanic Engineering,2013,38(4):701-717.
[71]Climent S,Sanchez A,Capella J V,et al.Underwater acoustic wireless sensor networks:advances and future trends in physical,MAC and routing layers[J].Sensors,2014,14(1):795-833.
[72]Ling J,Tan X,Yardibi T,et al.On Bayesian channel estimation and FFT-based symbol detection in MIMO underwater acoustic communications[J].IEEE Journal of Oceanic Engineering,2013,39(1):59-73.
Target detection with multi-sensor networks:a survey
YAN Yong-sheng,WANG Hai-yan,ZHANG Xiu,SHEN Xiao-hong
(School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China)
The decision fusion-based target detection algorithms are reviewed from the technical level for parallel multi-sensor network topologies.The likelihood ratio test method is categorized as determination of the statistics including the local sensor and data fusion center statistics and the thresholds solving including decision thresholds and data fusion center thresholds,and we carry out discussion on this basis.In theaspect of statistics determination with hard decision fusion system,the detection performance of different systems based on different fusion statistics under the ideal channel and the non-ideal channel is summarized and analyzed.The simulation results are also given to illustrate the performance of different fusion statistics.In the aspect of statistics determination with the soft decision fusion system,the performance metric is concluded.Besides,the decision space partition methods of local sensor nodes are compared and analyzed.When comes to the aspect of threshold solving,it can be summarized as approximation,iteration and Monte Carlo simulation.Further,the applications,advantages and disadvantages of these methods are also considered and compared.Finally,further research trends of decision fusion-based target detection are proposed.
signal and information processing;multi-sensor network;decision fusion;target detection;survey
TP 391
A
10.3969/j.issn.1001-506X.2015.03.01
闫永胜(1986-),男,博士研究生,主要研究方向为多传感器网络目标检测与定位。
E-mail:ysyan@mail.nwpu.edu.cn
王海燕(1965-),男,教授,博士研究生导师,博士,主要从事现代信号检测与现代信息处理、水声信息感知、水下电子对抗与智能电子系统、水声通信与组网、目标识别与定位跟踪。
E-mail:hywang@nwpu.edu.cn
张 秀(1990-),女,硕士研究生,研究方向为水声传感器网络目标定位。
E-mail:zhangxiu210@126.com
申晓红(1965-),女,教授,博士研究生导师,博士,研究方向为水声通信与组网;微弱信号检测与数字信号处理;目标探测、识别与定位;传感器(阵)与声学探测系统。
E-mail:xhshen@nwpu.edu.cn
1001-506X(2015)03-0473-12
2014 07 18;
2014 10 17;网络优先出版日期:2014 10 31。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141031.1028.002.html
国家自然科学基金(61401364);教育部博士点基金(20136102120013)资助课题
