传感器误差情况下的线性校正TOA定位算法

2015-06-05朱国辉冯大政向平叶

系统工程与电子技术 2015年3期

关键词：测量误差方根校正

朱国辉,冯大政,向平叶,周延

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)

传感器误差情况下的线性校正TOA定位算法

朱国辉,冯大政,向平叶,周延

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)

传统定位方法一般是在假设传感器位置信息准确已知的前提下进行的。然而在实际情形中,传感器位置信息往往含有随机误差,这些误差会严重影响目标的定位精度。针对这一问题,提出了一种存在传感器误差情况下的线性校正TOA定位算法。首先将非线性TOA定位方程组转化为一组关于目标位置的伪线性方程,利用加权最小二乘估计进行初始求解;然后在此基础上把伪线性方程组转化为关于估计偏差的求解问题,进而对初始解进行线性校正。在测量误差充分小的情况下分析了该算法的有效性。仿真结果表明该算法具有较好的定位性能。

定位;加权最小二乘估计;到达时间;传感器位置误差;线性校正

0 引言

定位技术在雷达、声纳、导航和传感器网络等领域[14]有着广泛的应用。就具体的定位参数信息而言,主要包括到达时间(time of arrival,TOA)、到达时间差(time difference of arrival,TDOA)、到达角(angle of arrival,AOA)和信号到达强度(received signal strength,RSS)等[58]。目前,常见的利用TOA测量信息对目标进行定位的算法有泰勒级数(Taylor-series,TS)法[9]、两级加权最小二乘(twostep WLS,TSWLS)法[10]、近似最大似然估计法[11]和多维尺度分析法[12]等。

然而,这些TOA定位方法都是在假设传感器位置信息准确已知的前提下进行的;而在实际应用中,传感器常常被安装在运动平台上,其位置信息往往含有随机误差。文献[13 14]的研究表明,传感器位置中含有的随机误差,即使在很小的情况下,也会严重降低目标的定位精度。文献[13]提出了一种两级加权最小二乘TDOA定位方法,该方法利用传感器位置误差统计信息设计加权矩阵来减轻传感器位置误差对目标定位精度的影响。在TDOA测量误差和传感器位置误差足够小时,该方法对远场目标的定位精度能够达到克拉美罗界(Cramer-Rao lower bound, CRLB)。文献[14]将两级加权最小二乘TDOA定位算法的思想应用到传感器位置误差情况下的TOA定位场景,所得定位算法在TOA测量误差和传感器位置误差充分小时对近场和远场目标的定位精度均能达到CRLB。但是该方法在第二级加权最小二乘估计求解时涉及到开方运算,产生的定位结果具有模糊性,并且可能出现虚数解。目前,文献[15]将总体最小二乘法应用到含有传感器位置误差的TOA定位中。然而,所得定位算法并不能达到CRLB,主要原因是没有考虑增广矩阵中误差分量之间的相关性,此时,总体最小二乘法并不能得到最优解。TS算法通过对非线性TOA定位方程进行一阶泰勒级数展开来实现线性化,需要预先给定一个迭代初始值;其收敛性依赖于初始值的选取和目标函数的非线性程度。当初始值接近真实值时,算法收敛速度快,定位精度高;但是在目标函数高度非线性并且初始值选择不好的情况下,容易落入到局部极小点,而且收敛性难以保证。为此,本文提出了一种传感器位置误差情况下的线性校正TOA定位算法,该算法首先利用加权最小二乘估计对伪线性定位方程组进行初始求解;然后将伪线性方程组转化为关于目标位置估计偏差的线性形式来进行求解;这里在TOA测量误差和传感器位置误差足够小的假设下分析了算法的有效性。仿真结果表明该算法与传统TOA定位算法相比具有较好的定位性能。

1 TOA定位模型

不考虑非视距传播的影响,根据TOA定位原理可得

式中,ti为测量值;toi表示信号从目标uo到传感器soi的真实时间;Δti为测量误差;c为信号传播速度。

将方程(2)两端同时乘以信号传播速度得

式中,ni=cΔti表示相应的距离测量误差。

将式(3)写成矢量形式

式中,ro=[ro1,ro2,…,roN]T;n=[n1,n2,…,nN]T。假定测量误差矢量n服从均值为零,协方差矩阵为Qr的高斯分布。

在实际应用中,传感器真实位置坐标soi一般未知,需要预先进行估计。假设估计的含有随机误差的传感器位置坐标si可以表示为

式中,Δsi为传感器位置随机误差,将式(5)表示为矢量形式

在传感器位置含有随机误差的情况下,基于多站TOA测量信息的定位问题即为根据方程组(4)和(6)尽可能准确地估计目标位置坐标uo。

2 线性校正TOA定位算法

2.1 加权最小二乘估计

由式(1)可知,式(3)是关于目标uo的非线性方程,将式(3)两边同时取平方,并利用式(1),经整理可得

当测量误差ni与2rio相比较小时,有。由于真实的传感器位置坐标sio也是未知量,根据式(5)可将soi表示为soi=si-Δsi,并代入式(7),经整理可得

式(9)为关于矢量φ的线性方程,其加权最小二乘解为

式中,加权矩阵W=E[ηηT]-1=(BQrBT+DQsDT)-1。将

2.2 线性校正TOA定位算法

式(9)在求解过程中假设φ1中分量uo与uoTuo互不相关,而事实上它们紧密相关。因此,由式(11)得到的目标位置^φ1(1∶3)只是一种粗估计,TSWLS算法[14]是在此基础上利用uo和uoTuo之间的关系对定位结果进行优化,但是由于涉及到开方运算,求得的定位结果具有模糊性,并且可能会产生虚数解。为此,这里提出一种线性校正TOA定位方法。考虑到实际值uo与估计值^φ1(1∶3)之间存在偏差,不妨设此偏差为φ2=Δφ1(1∶3),则实际位置为uo=^φ1(1∶3)-φ2。将uo=^φ1(1∶3)-φ2代入式(8)左端可得

对式(14)进行加权最小二乘求解可得

由式(15)得到的^φ只是初始估计^φ(1∶3)与真实目标uo21之间偏差的估计,校正后的目标位置为

下面利用一阶小误差扰动理论来求解校正后的目标位置估计^u的偏差及协方差矩阵。及式(16)可知目标位置估计^u的偏差为

在TOA测量误差与传感器位置误差充分小时,忽略高于一阶的扰动误差及偏差项,利用关系式式(14)可得

由式(17)可得

又由η=Bn+DΔs可知E[Δ^u]=03×1,即估计^u为无偏估计。由式(20)和W的定义可得估计^u的协方差矩阵为

2.3 性能分析

第二，反映价格因素的汇率和平均进口价格变量的系数是所有变量中系数最高的，这说明进口量对价格因素的变化非常敏感。

CRLB界是任意无偏估计所能达到的下界,由文献[16]可知基于TOA测量信息的定位问题的CRLB为

当误差矢量n和Δs与ri相比足够小时,即满足

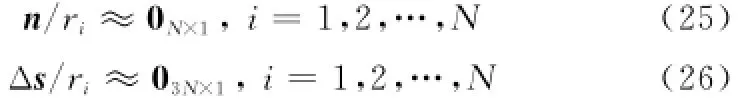
时,由式(16)得到的估计^u近似为有效估计。将cov(^u)转化为

令G3=B-1D,由矩阵求逆引理可得

令G4=B-1Go2,则cov(^u)为

根据Go2、B和D的定义可知矩阵G3和G4的第i行(i=1, 2,…,N)分别为

根据式(12)可知φ2可表示为n和Δs线性组合的形式,在条件式(25)和(26)下,即在n与Δs足够小时有

即也就是说,由式(16)所得估计^u在TOA测量误差和传感器位置误差足够小时近似为有效估计。

3 仿真实验

为了检验文中算法对目标位置估计的性能,将该算法与经典的TS法、TLS法、TSWLS法及克拉美罗界的仿真结果进行比较。

5个传感器位置坐标分别为

所有位置坐标单位均为m。同文献[14]一样,假设各个TOA测量值服从均值为零、方差为的高斯分布,则Qr=,传感器位置误差协方差阵设为Qs=σs2diag(1,1,1,2, 2,2,10,10,10,40,40,40,3,3,3),采用位置估计的均方根误差对各算法的定位性能进行衡量,其定义式为

式中,~uk为第k次目标位置估计;K=104表示蒙特卡罗仿真实验次数。

为了对比的公平,用式(11)所得初始定位结果计算文中算法和TSWLS法的权值及作为TS法的迭代初值。

仿真1 两目标位置坐标分别为uo1=[600,650,550]T和uo2=[2 000,2 500,3 000]T。图1(a)和图1(b)分别为各算法在σ2r=10-2情况下对两目标位置估计随σ2s变化时的均方根误差的统计结果。可以看出,即使在传感器位置误差较小时,TLS法的均方根误差也明显大于CRLB,这是因为它没有考虑增广矩阵中误差分量之间的相关性;而文中方法、TS法和TSWLS法的均方根误差均能够达到CRLB。随着测量误差的增加,各算法的估计均方根误差都会有所增加,而文中方法的估计均方根误差一直贴近CRLB,具有较好的定位性能。

仿真2 两目标位置坐标分别为uo3=[-400,-550, 450]T和uo4=[2 000,-2 500,-3 000]T。图2(a)和图2(b)分别给出了各算法在σ2s=10-2情况下对两目标位置估计随σ2r变化时的均方根误差的统计结果。在测量误差较小时,从图2中可以得出与仿真1中类似的结论,TLS法对两目标位置估计的均方根误差均明显大于CRLB,而其余算法能达到CRLB。随着测量误差的增加,各算法的估计均方根误差均有所增加。在测量误差较大时,TS法的均方根误差出现迅速增加的现象,这是因为在测量误差较大时,迭代初始值距真实值较远,在迭代过程中出现局部收敛或者发散的现象;而文中方法对uo3的估计均方根误差要小于TSWLS法,两种方法对uo4的估计均方根误差大小相当。

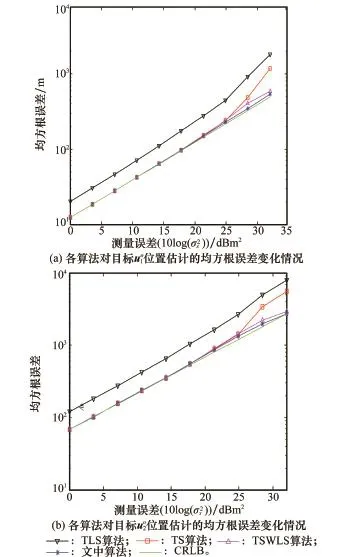
图1 各算法随变化时对和的定位性能示意图

TLS算法尽管也考虑了传感器位置误差,但是它忽略了增广矩阵中误差分量之间的相关性,定位性能并不理想; TSWLS法假设uo与r1相互独立,在第二级求解过程中涉及到开方运算,会产生模糊解,甚至可能产生复数解;而本文方法在第2.2节中对伪线性方程组进行了线性化,从仿真实验可以看出,在测量误差较大时本文算法要优于TSWLS法。由于TOA定位问题高度非线性,TS法很容易出现发散或者局部收敛的现象,这在仿真实验中也得到了验证。

图2 各算法随变化时对u和的定位性能示意图

4 结束语

传感器位置误差的存在会严重影响目标的定位精度,本文针对这一问题提出了一种估计传感器位置误差的线性校正TOA定位算法。算法通过两次加权最小二乘估计提高了目标定位精度。在TOA测量误差和传感器位置误差充分小时,该算法对目标的位置估计近似为有效估计。实验结果表明,该方法与传统TOA定位算法相比具有较好的定位性能。

[1]Fluckiger M,Neild A,Nelson B J.Optimization of receiver arrangements for passive emitter localization methods[J].Ultrasonics,2012,52(3):447-455.

[2]Win M Z,Conti A,Mazuelas S,et al.Network localization and navigation via cooperation[J].IEEE Communications Magazine,2011,49(5):56 62.

[3]Gholami M,Cai N X,Brennan R W.Evaluating alternative approaches to mobile object localization in wireless sensor networks with passive architecture[J].Computers in Industry,2012,63(9): 941-947.

[4]Jin J B,Wu N,Yang Q.Sensor placement strategies for TDOA location system based on semidefinite relaxation[J].Journal of Circuits and Systems,2013,18(2):133-138.(金家保,吴宁,杨全.基于半定松弛的时差定位系统优化布站算法[J].电路与系统学报,2013,18(2):133-138.)

[5]Liu C F,Yang J,Wang F S.Joint TDOA and AOA location algorithm[J].Journal of Systems Engineering and Electronics, 2013,24(2):183-188.

[6]Xu B,Chen J Y,Zhong X P.New cellular location algorithm based on TLS-assisted Taylor series expansion in TOA mode[J]. Systems Engineering and Electronics,2011,33(6):1397-1402. (徐波,陈建云,钟小鹏.TOA模式下TLS辅助泰勒级数展开的蜂窝定位新算法[J].系统工程与电子术,2011,33(6):1397-1402.)

[7]Huang J,Xue Y B,Yang L.An efficient closed-form solution for joint synchronization and localization using TOA[J].Future Generation Computer Systems,2013,29(3):776-781

[8]Shen G W,Zetik R,Thoma R S.Performance comparison of TOA and TDOA based location estimation algorithms in LOS environment[C]∥Proc.of the 5th Workshop on Positioning, Navigation and Communication,2008:71 78.

[9]Foy W H.Position-location solution by Taylor-series estimation[J]. IEEE Trans.on Aerospace and Electronic Systems,1976,12(2): 187-194.

[10]Chan Y T,Ho K C.A simple and efficient estimator for hyperbolic location[J].IEEE Trans.on Signal Processing,1994, 42(8):1905-1915.

[11]Chan Y T,Hang H Y C,Ching P C.Exact and approximate maximum likelihood localization algorithms[J].IEEE Trans. on Vehicular Technology,2006,55(1):10-16.

[12]Wei W H,Wan Q,Chen Z X,et al.A novel weighted multidimensional scaling analysis for time of arrival based mobile location[J].IEEE Trans.on Signal Processing,2008,56(7): 3018-3022.

[13]Ho K C,Lu X,Kovavisaruch L.Source localization using TDOA and FDOA measurements in the presence of receiver location errors:analysis and solution[J].IEEE Trans.on Signal Processing,2007,55(2):684-696.

[14]Ma Z H,Ho K C.TOA localization in the presence of random sensor position errors[C]∥Proc.of the IEEE International Conference on Acoustics,Speech,and Signal Processing, 2011:2468-2471.

[15]Wang A H,Yang K,An J P,et al.Total least-squares algorithm for time of arrival based wireless sensor networks location[J]. IEICE Trans.on Fundamentals of Electronics,Communications and Computer Sciences,2011,94(9):1851 1855.

[16]Sun M,Ho K C.Refining inaccurate sensor positions using target at unknown location[J].Signal Processing,2012,92(9): 2097-2014.

Linear-correction TOA localization algorithm with sensor location errors

ZHU Guo-hui,FENG Da-zheng,XIANG Ping-ye,ZHOU Yan
(National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China)

Conventional location algorithms are based on the postulation that the sensor locations are exactly known.However,in practical situations,the sensor positions generally include random errors,which can considerably reduce the source localization accuracy.To tackle this problem,a new time of arrival(TOA)positioning algorithm based on the linear-correction technique is proposed.The proposed algorithm firstly reorganizes the nonlinear TOA equations into pseudo-linear ones and the initial target position estimation is obtained by using weighted least-squares estimatets.Then a linear-correction technique is used to correct the initial position estimate.The effectiveness of the proposed method is theoretically analyzed under sufficiently small noise postulation.Simulation study validates the good performance of the proposed algorithm.

location;weighted least square estimate;time of arrival(TOA);sensor position error;linearcorrection

TN 92

10.3969/j.issn.1001-506X.2015.03.04

朱国辉(1987-),男,博士研究生,主要研究方向为无源定位与跟踪。E-mail:zhugh@stu.xidian.edu.cn

冯大政(1959-),男,教授,博士,主要研究方向为研究方向为盲信号处理、雷达信号处理、无源定位和阵列信号处理。

E-mail:dzfeng@xidian.edu.cn

向平叶(1987-),女,硕士研究生,主要研究方向为空时信号处理,无源定位。

E-mail:yutong.324@163.com

周延(1988-),男,博士研究生,主要研究方向为空时信号处理。

E-mail:spainraul123@126.com

网址:www.sys-ele.com

1001-506X(2015)03-0498-05