基于融合Dijkstra的凸壳算法的舰载机机库调运规划

司维超,齐玉东,韩 维

(1.海军航空工程学院兵器科学与技术系,山东烟台264001; 2.海军航空工程学院飞行器工程系,山东烟台264001)

基于融合Dijkstra的凸壳算法的舰载机机库调运规划

司维超1,齐玉东1,韩 维2

(1.海军航空工程学院兵器科学与技术系,山东烟台264001; 2.海军航空工程学院飞行器工程系,山东烟台264001)

为解决舰载机在特殊的机库环境中调运路径规划问题,提出了一种融合Dijkstra方法的凸壳算法。首先,建立了飞机机库调运的数学模型以及相关基础模型,为算法应用提供基础。其次,给出了利用凸壳算法进行路径规划的执行机制,并利用其建立了飞机调运可行路径有向图。然后,利用Dijkstra方法对该可行路径有向图进行最短路径求解,最终给出最优路径。最后,将该方法应用于库兹涅佐夫号航母飞机机库调运。结果表明,该方法原理正确,且能够较好地给出最优路径。

飞机调运;路径规划;Dijkstra;凸壳算法;最优路径

0 引 言

航空母舰在当今世界作用越来越重要,其绝大多数作战使命都需要并且只能由飞机来承担和完成。通过对飞机进行有效的保障,可以大大提高航空母舰的作战能力[1]。飞机保障过程中的一个重要方面是对其在机库甲板上进行有序地移动[2]。鉴于机库甲板面积较小,为了保证安全,必须进行合理规划[3]。

随着现代战争的节奏加快,航母作用日益突出,而提高其舰载机调运效率显得尤为重要[4]。在满足安全约束条件下,根据机库特殊情况,动态给出舰载机移动路线需要进一步研究。

国外针对飞机的调运主要依靠人工指挥[5]。此种方法不可避免会导致效率低下及出现错误。另外,我国尚未具备成熟的飞机机库调运经验,亟待进行研究。为此本文通过对飞机机库调运问题进行建模,并利用融合Dijkstra方法[6]的凸壳算法[78]对舰载机机库调运问题进行求解,提高了效率和准确性。

1 飞机机库调运路径规划问题建模

飞机在机库中调运路径规划问题可以看为在满足约束条件下的最短路求解问题[9]。由于机库的环境相对舰面来说更狭小,所以在调运飞机时要满足的约束条件也更多更严格[10]。数学模型建立如下:

目标函数

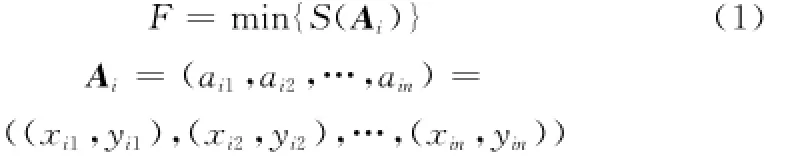
约束条件

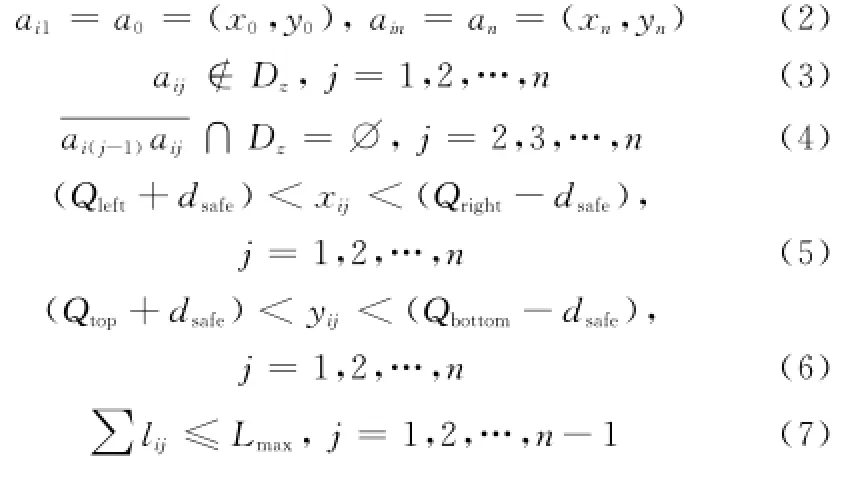
式中,F为调运所要达到的目标效果,即在满足约束条件下,尽可能缩短飞机在机库内的行走路径,从而缩短飞机出库时间;S为飞机沿某条机库行走路径的距离;Ai为第i条舰载机行走路线,aij为第i条行走路线中的第j个中间路径节点,规定其位于机库坐标平面内的坐标为(xij,yij);n为路径节点的个数;a0为路径的起始点;an为路径的终点; Dz表示当前状态下机库中所有的障碍物区域的集合;Qleft表示机库右侧边界所表示的X轴值;Qright表示机库左侧边界所表示的X轴值;Qtop表示机库上侧边界所表示的Y轴值;Qbottom表示机库下侧边界所表示的Y轴值;dsafe表示最小安全间隔,即不与机库四周发生碰撞的最小间距;lij为飞机第i条路径的第j个移动路径段的长度;Lmax为所要求的起点和终点之间最大不能超过的路径总长度[11]。

由上述可知,式(2)表明了飞机移动的起点和目的地。式(3)表示所规划的飞机行走路线不能与障碍物发生碰撞。式(4)表示所规划出的最终路径中相邻两个节点的连线不能与任何障碍物相交。式(5)和(6)表示飞机路径节点不能与机库四周墙壁发生碰撞。式(7)表示所规划的飞机行走路线的距离必须具有上限约束。

2 基于融合Dijkstra的凸壳算法的最短路径规划

2.1 环境建模

(1)机库模型的建立

本部分主要对飞机调运所需的机库环境进行建模,给出整个大环境。此处可以近似将机库看作为一个矩形区域。例如针对库兹涅佐夫号航母机库矩形区域如图1所示。

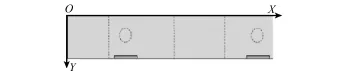
图1 机库模型

(2)飞机实体模型和障碍物凸壳模型建立

为了简化问题,用包围飞机最大边界的简单凸多边形来表示舰载机,如图2所示,图中,Ga、Gb和Gc为按照比例缩放时的相关尺寸。

图2 飞机凸多边形模型

为了能够将运动实体简化为一个质点,方便凸壳算法的执行,在规划路径时,首先需要将障碍物凸多边形进行扩充,建立障碍物凸壳多边形[12],如图3所示,图中各参数可以通过测量给出。

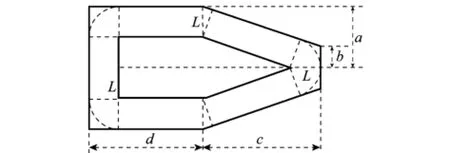
图3 飞机凸壳模型

(3)建立舰载机位姿模型

针对每一个障碍物凸壳模型,当确定其状态(位置、朝向等)时需要用到二维平面变换。具体如图4所示。

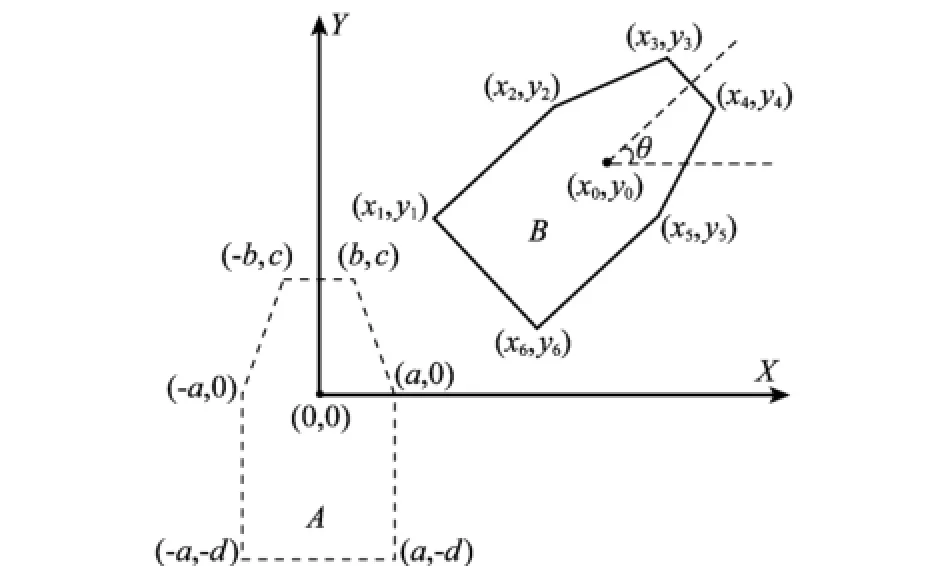
图4 障碍物位姿模型

令A模型中任意一顶点坐标为(x,y),则对应新的坐标计算过程为

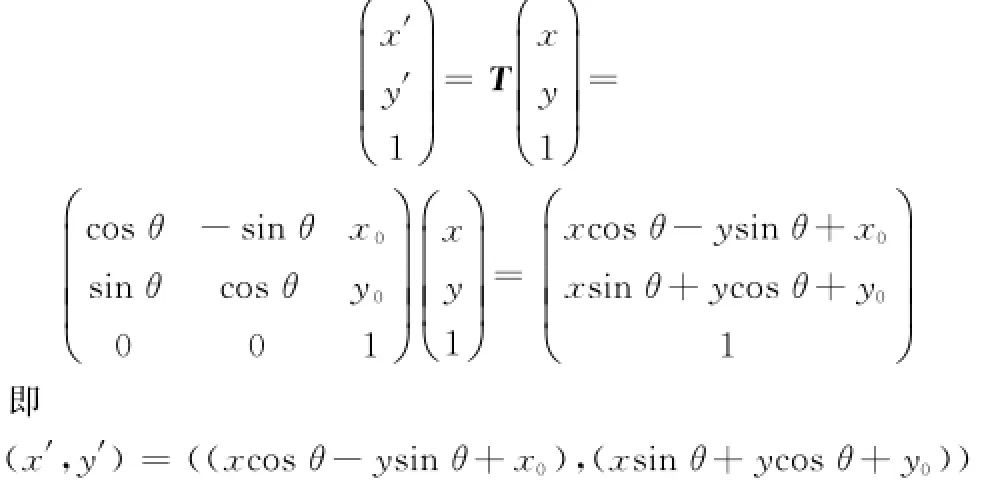
(4)碰撞检测模型的建立

此处需要对路径节点进行碰撞检测,主要是判断所规划出移动路径上的节点是否位于其他障碍物内部,即是否发生碰撞[1314]。具体步骤如下:

步骤1 明确当前机库中各个障碍物状态及路径节点坐标M(a,b),进行初步判断。依据为通过判断该障碍物的最左侧点和最右侧点是否位于X=a直线两侧,由此可以减少参与点碰撞检测的障碍物数量。

步骤2 对筛选出来的障碍物与点M(a,b)进行最终点碰撞检测。以某个障碍物模型A为例,示意图如图5所示。

图5 碰撞检测示意图

(1)分别比较A的每一条边与直线X=a的关系,看是否有交点。令某边的端点为(xi,yi)和(xj,yj),则判断依据如下:

①(max(xi,xj)≥a)and(min(xi,xj)＜a)表明X=a直线穿过该边或其右端点;

②(max(xi,xj)＞a)and(min(xi,xj)≤a)表明X=a直线穿过该边或其左侧端点。

(2)计算交点。据比例公式(a-xi)/(xj-xi)=(yib1)/(yi-yj),可以得出b1=yi-(a-xi)(yi-yj)/(xjxi),则所求交点为(a,b1),示意图如图6所示。

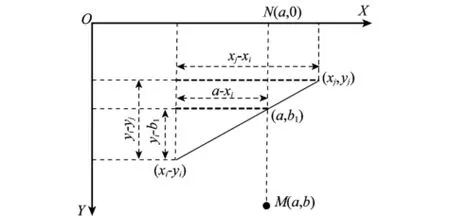
图6 求交示意图

(3)针对障碍物每条边分别进行上述比较,使得最后可以给出一个交点集合(无重复,且因为为凸多边形所以最多有两个交点,记为(a,b1)和(a,b2))。

(4)进行最终的检测:若min(b1,b2)＜y＜max(b1,b2),表明M点介于两交点之间,另据凸多边形的性质可知,M点必位于障碍物内部,也即此时会出现碰撞现象;否则不发生。

2.2 基于凸壳算法的可行路径有向图建模

(1)初始化机库布局环境,明确运动实体及调运目的地,建立障碍物凸壳模型。

根据飞机位姿模型确定机库环境。假设有12架飞机(以Z1-Z12表示),令Z1作为运动实体(简化为一质点),位置D作为调运目的地,并对障碍物执行凸壳扩充,如图7所示。

图7 假设的机库局部凸壳环境模型

图7中,四周虚线表示机库墙壁进行凸壳内扩后的界限。运动实体Z1的运动轨迹不能与障碍物凸壳模型及四周虚线框有碰撞,即其间隔必须大于等于最小安全距离。

(2)执行凸壳算法,寻求可行路径有向图。

凸壳算法主要是基于两点之间线段距离最短的思想。首先,建立起点和终点的连线,如果该连线不与任何障碍物凸壳模型相交,则其即为待规划的最优路径;否则,连线穿过障碍物凸壳模型,则该连线将障碍物分为上下两部分,此时可以将路径规划问题转换为求解障碍物上下两部分顶点集的凸包问题,从而可以得到上下两条最优路径(假如存在的话)。其次,对当前规划出路径上相邻两个节点间的路径段重复执行以上的路径规划,直至所有路径段均不与障碍物发生碰撞。最后,按照所记录的无碰撞路径节点建立路径有向图。

①建立起点Z1和终点D之间的有向线段Z1D,确定线段Z1D所穿越的障碍物。

由图7可知,有向线段Z1D直接穿过障碍物Z6和Z7,但是由于障碍物Z5与Z6有交集,在计算凸包时必须把Z5算入线段Z1D间接穿过的障碍物,故最终被穿越的障碍物集合为R={Z5,Z6,Z7}。

②以线段Z1D为分界线,将R中障碍物分为上下两部分,并对各自的顶点集合排序。

判断障碍物集合R中各障碍物顶点属于“上半部分”或者“下半部分”的依据为:假设经过Z1点和D点直线方程为f(x,y)=ax+by+c,且待判断的某顶点坐标为(xi,yi),则f(xi,yi)=(axi+byi+c)≥0,表示该顶点位于线段Z1D上部;f(xi,yi)=(axi+byi+c)＜0,表示该顶点位于线段Z1D下部。

由图7可知,点ui(i=1,2,…,16)属于上部;点di(i= 1,2)属于下部。分别对两顶点集按照“先按X坐标升序,当X坐标相同时,再按Y坐标升序”的原则进行排序,结果为:上部顶点集Up Points={Z1,u1,u2,u3,u4,u5,u6,u7,u8,u9,u10,u11,u12,u13,u14,u15,u16,D};下部顶点集Down-Points={Z1,d1,d2,D}。

③分别计算Up Points的上凸包和DownPoints的下凸包。

所谓凸包是指顶点集中凸点的集合。在进行凸包搜索时,需要判断相邻3个顶点的排列顺序(顺时针或逆时针)。这里采用矢量叉积的方式进行判断,具体如下:

点P0、P1、P2按照顺时针的顺序排列,则P1点为上凸包点,依据为(P2-P0)×(P1-P0)＜0;点P0、P1、P2按照逆时针的顺序排列,则P1点为下凸包点,依据为(P2-P0) ×(P1-P0)＞0;点P0、P1、P2共线,P1点不为凸包点,依据为(P2-P0)×(P1-P0)=0。

针对图7所示情况,对其顶点集Up Points按照顺时针判断方式求其上凸包顶点;对其顶点集Down Points按照逆时针判断方式求其下凸包顶点。结果为:上凸包点集Up-Bulgy Points={Z1,u1,u4,u6,u9,u11,u13,u15,D};下凸包点集DownBulgy Points={Z1,d1,d2,D}。

④依次连接上凸包及下凸包中各顶点,并进行初步优化。将上下凸包各个顶点连接起来,如图8中虚线所示。

图8 初始凸包图

此时得到两条初始规划路径UpRoute(Z1,D)和DownRoute(Z1,D)。但是,由图8可以看出,这两条路径并不是完全满足要求的,例如上凸包中的点u4位于障碍物Z5内部等。为此需要对UpRoute(Z1,D)和DownRoute(Z1, D)分别进行碰撞检测。

具体如下:

步骤1 对上下凸包执行碰撞检测,去除不合格点。经检测可知,此处上凸包中的点u4与障碍物Z5发生碰撞,所以将其进行排除。点u9虽然不位于障碍物内部,但是线段u6u9穿越障碍物,所以将其进行排除。

上凸包点集Up Bulgy Points={Z1,u1,u6,u11,u13,u15, D};下凸包点集Down Bulgy Points={Z1,d1,d2,D}。

步骤2 对新的上下凸包点集执行优化操作,去除冗余点。由于飞机在机库中调运时,应该尽量避免频繁转向。为此对上下凸包分别进行检查可知,上凸包中点u13是多余的,可以删掉。此时新的上下凸包点集为:上凸包点集Up-Bulgy Points={Z1,u1,u6,u11,u15,D};下凸包点集Down-Bulgy Points={Z1,d1,d2,D}。

利用线段连接上下新凸包各个顶点,如图9中虚线所示。

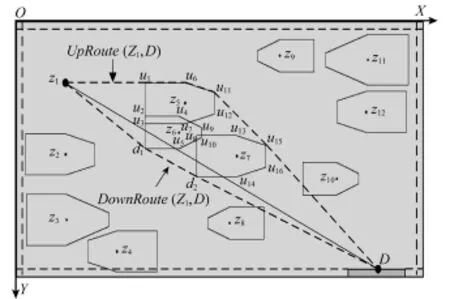
图9 优化后凸包图

图10 最终可行路径有向图

2.3 基于Dij kstra方法的最短路径求解

利用凸壳算法最终可以得出可行路径有向图,其复杂情况完全取决于参与凸壳运算的障碍物的数量,且不同的起点和终点其可行路径有向图也互不相同。为了能够覆盖所有可能情况,此处将所有的可行路径有向图求最优路径问题统一看为赋权有向图求最短路问题,从而可以利用统一的算法进行求解。目前对于所有非负权有向图求最短路最好的方法是Dijkstra方法[15],为此本文采用该算法求解飞机机库调运可行路径有向图的最短路径。对图10所示的可行路径有向图进行简化提取,如图11所示。其中的权值取两点间距离。

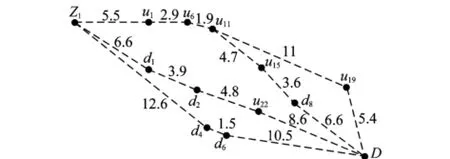
图11 简化后赋权可行路径有向图

Dijkstra方法的具体步骤如下:

步骤1 初始化。给定赋权有向图D=(V,A)。用P, T分别表示某个点的P标号、T标号,Si表示第i步时,具P标号点的集合。为了在求出从vs到各点的距离的同时,也求出从vs到各点的最短路,给每个点v以一个λ值,算法终止时,如果λ(v)=m,表示在从vs到v的最短路上,v的前一个点是vm;如果λ(v)=M,则表示D中不含从vs到v的路;λ(v)=0表示v=vs。

初始i=0时,令S0={vs},P(vs)=0,λ(vs)=0;对每一个v≠vs,令T(v)=+∞,λ(v)=M,k=s。

步骤2 如果Si=V,算法终止,这时,对每个v∈Si, d(vs,v)=P(v);否则转入步骤3。

步骤3 考查每个使(vk,vj)∈A且vj∉Si的点vj。如果T(vj)＞P(vk)+ωkj,则把T(vj)修改为P(vk)+ωkj,把λ(vj)修改为k;否则转入步骤4。

对图11所示的可行路径有向图执行进行Dijkstra求解可知,从Z1到D的最短路为(Z1,d1,d2,u22,D),长度为23.9。

3 实例仿真

将上述求解过程实际应用于求解库兹涅佐夫号航母机库飞机的调运。

(1)确定机库初始调运环境,以及运动实体和目的地。假设库兹涅佐夫号航母的某种机库布局如图12所示,且需要将飞机S调运至升降机D。

图12 实例之机库局部布局环境图

(2)建立机库障碍物凸壳环境模型,如图13所示。

图13 实例之机库凸壳环境模型

(3)执行融合Dijkstra方法的凸壳算法,求最优路径。

图14中粗折线为所规划的最优路径,与实际最优路径基本吻合,这表明本文所提的方法是可行的。对不同情况下的飞机分别进行路径规划,都能够得到较好的结果。由此可知,本文所述方法可较好地对飞机机库调运问题进行求解,所得结果基本符合实际要求。另外,算法执行的复杂程度主要取决于参与运算的障碍物数量,而与路径长度关系不大,为此在不同数量障碍物下对算法分别执行50次独立路径规划运算,提取规划时间的统计结果如图15所示。由图15可知,当有6个障碍物参与运算时,所需计算时间平均为28 s,所以计算效率基本符合实际要求。

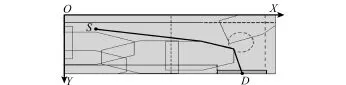
图14 实例之最优调运路径

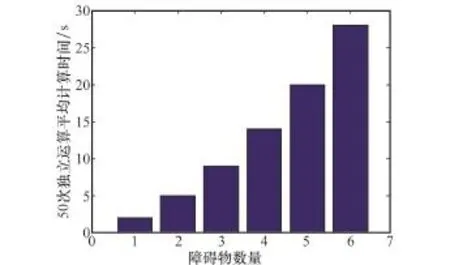
图15 平均计算时间

4 结 论

将飞机机库调运问题转化为在满足特殊约束条件下的最短路径求解问题,提出了一种融合Dijkstra方法的凸壳算法,并对最短路进行规划,克服了以往靠人工引导的缺陷。通过将该方法实际应用于库兹涅佐夫号航母飞机机库调运,结果表明,该方法原理正确,且所得结果符合实际。

[1]Han W,Wang Q G.Conspectus of aircraft carrier and carrier plane[M].Yantai:Naval Aeronautical and Astronautical University Press,2009:37-41.

[2]Duan PP,Nie H.Effect of carrier movement on aircraft’s landing and arresting performance[J].Journal of Nanchang Hangkong University(Natural Sciences),2012,26(1):53-60. (段萍萍,聂宏.航母运动对飞机着舰拦阻性能的影响分析[J].南昌航空大学学报(自然科学版),2012,26(1):53-60.)

[3]Fu Y G,Ding M Y,Zhou C P.Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV[J].IEEE Trans.on Systems, Man and Cybernetics-Part A:Systems and Humans,2012,42 (2):511-526.

[4]Authority of the Chief of Naval Operations.CV Flight/Hangar Deck NATOPS Manual[R].Washington,D C:Authority of the Chief of Naval Operations 2001.

[5]Johnston J S.A feasibility study of a persistent monitoring system for the flight deck of U.S[D].USA:Navy Aircraft Carriers Department of the Air Force Air University,2009.

[6]Deng Y,Chen Y,Zhang Y,et al.Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment[J].Applied Soft Computing,2012,12(3):1231-1237.

[7]Liu R,Fang B,Tang Y Y.A fast convex hull algorithm with maximum inscribed circle affine transformation[J].Neurocomputing,2012,77(1):212-221.

[8]Brun C,Dufourd J F,Magaud N.Designing and proving correct a convex hull algorithm with hypermaps in Coq[J].Computational Geometry,2012,45(8):436-457.

[9]Hu Y M,Liu W M.Multi-constrained shortest path model and soving[J].Journal of Hunan University of Science&Technology(Natural Science Edition),2010,25(1):87 90.(胡耀民,刘伟铭.多约束最短路模型与求解[J].湖南科技大学学报(自然科学版),2010,25(1):87-90.)

[10]Sun S N.Modern aircraft carrier[M].Shanghai:Shanghai Popular Science Press,2000:1-50.(孙诗南.现代航空母舰[M].上海:上海科学普及出版社,2000:1 50.)

[11]Zheng C W,Yan P,Ding M Y,et al.Route planning for air vehicles[M].Beijing:National Defense Industry Press,2008: 70-79.(郑昌文,严平,丁明跃,等.飞行器航迹规划[M].北京:国防工业出版社,2008:70-79.)

[12]Yang Y,Liu Y C.A path planning algorithm based on convex hull for autonomous service robot[J].Transaction of Beijing Institute of Technology,2011,31(1):54-58.(杨毅,刘亚辰.一种基于凸壳的智能服务机器人路径规划算法[J].北京理工大学学报,2011,31(1):54-58.)

[13]Prete J,Mitchell J S B.Safe routing of multiple aircraft flows in the presence of time-varying weather data[C]∥Proc.of the AIAA Guidance,Navigation,and Control Conference,2004: 1-21.

[14]Dieguez A R,Sanz R,Lopez J.Deliberative on-line local path planning for autonomous mobile robots[J].Journal of Intelligent and Robotic Systems,2003,37(1):12-19.

[15]Xiong D G,Hu Y W.A matrix method of solving shortest path using Dijkstra algorithm[J].Journal of Henan Polytechnic University,2011,30(5):608-612.(熊德国,胡勇文.用Dijkstra算法求解最短路的矩阵方法[J].河南理工大学学报, 2011,30(5):608- 612.)

Carrier plane transportation in hangar based on convex hull algorithm combined with Dijkstra

SI Wei-chao1,QI Yu-dong1,HAN Wei2
(1.Department of Ordnance Science and Technology,Naval Aeronautical and Astronautical University,Yantai 264001,China;2.Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University,Yantai 264001,China)

In order to solve the carrier plane moving route planning problem in special hangar environment, a new convex hull algorithm combined with Dijkstra is proposed.Firstly,the mathematic model of the carrier plane moving problem and correlative basic models are established,which supply foundation for the using of the algorithm.Secondly,the executive mechanism of using the convex hull algorithm to plan routes is provided, which is used to establish the carrier plane moving route directed graph.Then the best route could be found by using Dijkstra to operate on the directed graph.Finally,the method is used to solve the carrier plane moving route planning problem in hangar of the Kuznetsov aircraft carrier.Simulation results indicate that the principle of the method is correct and it performs well for getting the best route.

carrier plane moving;route planning;Dijkstra;convex hull algorithm;best route

TP 202

A

10.3969/j.issn.1001-506X.2015.03.17

司维超(1984-),男,讲师,博士,主要研究方向为舰载机技术研究及应用。E-mail:sxwxc1984@163.com

齐玉东(1974-),男,教授,博士,主要研究方向为指挥控制及优化。E-mail:LuckydevilSI@163.com

韩 维(1970-),男,教授,博士,主要研究方向为舰载机技术研究及应用。

E-mail:Luckydevilhan@163.com

网址:www.sys-ele.com

1001-506X(2015)03-0583-06

2014-03-24;

2014-07-24;网络优先出版日期:2014-09-28。

网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20140928.1716.019.html