Ad-hoc网络中基于博弈论和粒子群优化的协作算法

2015-06-05张佳岩赵洪林

系统工程与电子技术 2015年3期

关键词：接入点纳什中继

张闯,张佳岩,赵洪林

(哈尔滨工业大学通信技术研究所,黑龙江哈尔滨150080)

Ad-hoc网络中基于博弈论和粒子群优化的协作算法

张闯,张佳岩,赵洪林

(哈尔滨工业大学通信技术研究所,黑龙江哈尔滨150080)

为了促使Ad-hoc网络中的“自私”节点进行合作,提出了一种基于博弈论和粒子群优化的协作算法(Nash Bargaining of game theory and particle swarm optimization,NGPSO)在算法的第一阶段,源节点通过对中继节点转发的数据进行价格补偿,从而达到使中继节点参与合作的目的。将源节点的最优出价归结为纳什谈判问题,得到具有帕累托最优的激励价格,保证源节点和中继节点在合作中同时获得最佳收益;在算法的第二阶段,中继节点在获得源节点的最优出价后,通过粒子群优化算法得到最优的转发功率,使其合作收益增益最大。仿真表明,和随机价格激励相比,所提出的NGPSO算法能使源节点和中继节点达到最优收益;和中继节点固定功率转发相比,所提出的NGPSO算法,能显著提高源节点的能量效率和中继节点的收益,同时在适当设置中继节点转发功率的搜索空间时,可以保证总的能量效率。

协作算法;博弈论;粒子群优化;能量效率

0 引言

近年来,关于Ad-hoc网络中节点间的协作问题得到了越来越多的关注。Ad-hoc网络除可以表现出“无私”的合作特性外,还可能表现出不合作的“自私”特性。在Ad-hoc网络中,如果节点既要进行自身的数据传输,又要为其他节点提供路由选择和数据转发服务,则当其为其他节点服务时,势必要消耗自身的能量和带宽资源,节点往往表现出不合作的行为。研究表明,当网络中的不合作节点数目占到全网总结点的10%到40%时,网络的平均吞吐量会严重下降16%至32%[1]。因此,如何建立有效的激励机制,促进节点间合作是一个亟待解决的问题。

为了促使节点进行合作型的数据转发,文献[2-3]提出了针锋相对(Tit-for-Tat)的协作策略,该策略使网络中的节点根据历史统计来判断是否进行合作。然而,针锋相对策略是一种反复博弈的过程,当节点在网络中出现的次数很少时,该策略可能失效。文献[4]提出了一种基于价格补偿的激励合作策略,通过接入点对中继节点转发的数据量进行价格补偿来激励中继节点帮助源节点转发数据。该策略中,中继节点在合作中获得的收益有时会低于非合作时获得的收益,这是由该策略最大化接入点收益造成的。文献[5]对文献[4]的工作进行了改进,将接入点对中继节点做出的价格补偿转变为由源节点做出,从而使中继节点在合作中获得的收益始终大于非合作中获得的收益;文献[6]针对一个源节点和多个中继节点模型,采用非合作博弈方法,首先由中继节点作为卖方决定带宽价格,之后源节点根据带宽价格决定其带宽需求。该策略本质上是一个Stackelberg博弈模型,文献[6]证明了存在纳什均衡,并提出了一种分布式算法计算纳什均衡,但同时文献[6]也提到纳什均衡并不是最有效率的;文献[7]针对一个时分复用系统,采用合作博弈的方法,提出了一种基于交换时隙资源的激励合作机制;文献[8]对文献[7]的工作进行扩展,提出了一种联合时隙和功率分配的协作方法;文献[9]同样在基于资源交换进行协作的基础上,提出了一种快速粒子群算法从而获得合作博弈的纳什均衡。文献[4-6]是基于非合作博弈的方法对激励合作机制进行了研究,非合作博弈的纳什均衡有可能是无效率的,即不具有帕累托最优性,不能一定保证所设计的效用函数最优;文献[7-9]采用合作博弈理论建立了激励合作的机制,但基于资源交换建立的合作机制是建立在双方都有闲置资源的基础上的,这限制了其应用范围。

不同于以上研究,为了促使Ad-hoc网络中的“自私”节点参与合作,本文提出了一种基于博弈论和粒子群优化的协作算法(Nash bargaining of game theory and particle swarm optimization,NGPSO)。本文主要贡献是解决了激励合作机制中的两个关键问题:如何激励合作及何时合作。①对于如何激励合作问题,通过源节点对中继节点转发的数据进行价格补偿,从而达到促使网络中的“自私”节点进行合作的目的。本文将源节点的最优激励价格归结为纳什谈判问题,避免了传统非合作博弈方法得到的纳什均衡可能不是最佳策略的问题,确保源节点的激励价格具有帕累托最优性,从而使源节点和中继节点在合作中获得的收益最优;②对于何时合作问题,通过基于纳什谈判的最优激励算法,当源节点和中继节点合作获得的收益大于非合作的收益时,双方达成合作;③进一步,为了提高中继节点的收益,采用粒子群优化算法计算了中继节点的最优转发功率。

1 系统模型

激励合作机制的建立依赖于初始的网络拓扑结构,本文主要研究如何得到源节点的最优出价和中继节点的最优转发功率,因此采用一种简单的网络模型,如文献[4]所描述,两个位置相近的对等用户被划为一簇,其中用户1作为发起协作请求的源节点,用户2作为中继节点,具体模型如图1所示。假设系统是以频分复用的方式工作,用户之间不产生干扰,并且源节点和中继节点的可用带宽为W Hz,采用全向天线进行数据的接收和发送。为了激励中继节点进行传输,源节点对中继节点转发的数据进行价格补偿,从而使中继节点有动力参与合作。模型中,用户1的部分数据被中继节点转发,用户2的数据直接传输给基站。假设用户1请求协作传输的数据带宽占总带宽W的比例为n(n∈[0,1]),除了协作传输数据之外,用户1的可用带宽W全部用来和基站进行数据传输。为了激励用户2进行数据转发,用户1对通过用户2传输的数据进行价格补偿,每单位数据补偿金额为u。假设用户2愿意转发的数据带宽占总带宽W的比例为n,用剩下的1-n的带宽直接向目的节点发送其他数据。假设接入点(AP)对用户1和用户2每单位数据收费为λ。

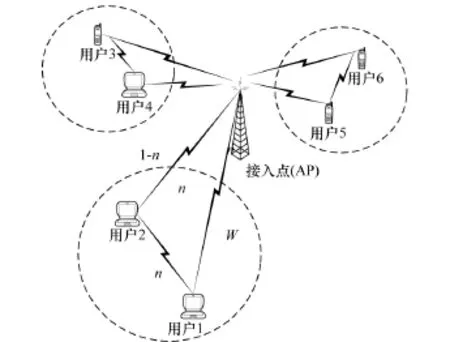
图1 系统模型

从用户1的角度,为了获得更大的收益,它希望尽可能地减少每单位数据价格u;而从用户2的角度,则希望尽可能地提高每单位数据价格u,本文采用纳什谈判的方法达到一个最优折中。同时,用户2在获得用户1的出价后,需要考虑其自身性能(功率)及获得回报(价格)之间的平衡,因此需要决定其最佳的转发功率。下面对以上两个问题进行分析以确定这两个参数。

2 能量效率

为了能够定量地研究系统的性能,需要一个恰当的衡量标准。文献[10-11]在用博弈论研究CDMA系统功率控制时,给出了一种衡量系统性能的能量效率函数,其定义为

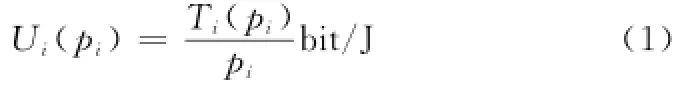
该定义可以解释为:每消耗一单位能量能够正确接收的数据量。为了使该定义能够符合实际,文献[10]规定了其需要满足的特性:当p→∞时,Ui(pi)→0;当p→0时, Ui(pi)→0。也就是说当发射功率为无穷大或者是零时,用户的能量效率值为0,这是符合常识的。Ti(pi)为有效传输信息量,在文献中被定义为

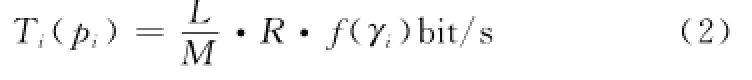
式中,M为发送数据量;L为信息比特;M-L比特用作错误检测。f(γi)为效率函数,其定义和传统的表示一个数据帧被正确接收的概率稍有不同:

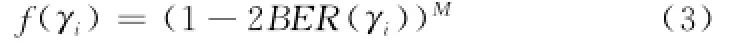
式中,γi为接收信噪比;BER(γi)为误比特率;当采用非相干2FSK调制时BER(γi)=1/2exp(-γi/2)。f(γi)之所以采取如此定义,是为了使发射功率为无穷大或者是零时,用户的能量效率为0,具体证明可以参照文献[10]。

为分析方便,有R=ηW,其中η(b/(s·Hz))为频谱效率,当采用2FSK调制时,η2FSK=1。因此式(2)可以表示为

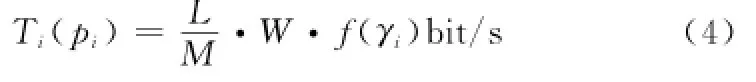
由此,可以定义用户1的能量效率为

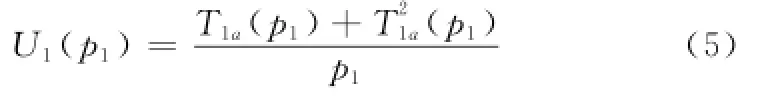
式中,T1a(p1)为用户1直接传输到接入点的有效吞吐量,表示为

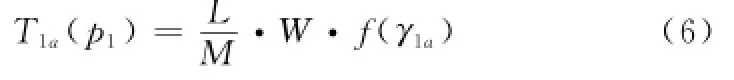
式中,γ1a为用户1到接入点的信噪比;T21a(p1)为用户1通过用户2中继的有效吞吐量,因为用户2中继的数据占自身比例为n,因此)表示为

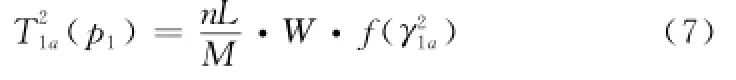
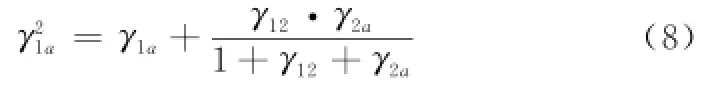
式中,γ12、γ2a分别为用户1到中继节点,中继节点到接入点的信噪比。用户2的效用函数为

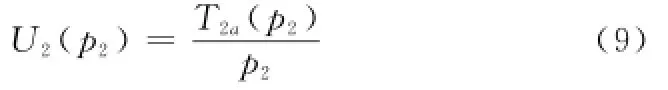
为用户2用带宽比例为1-n传输自己数据时的有效吞吐量。

3 收益函数

对于用户1来说,为了促使用户2进行合作,需要对用户2进行补偿,即支付用户2每单位数据μ的价格,同时,接入点对用户1的收费为每单位数据λ。可以看出,用户1获得的好处为U1(p1),而付出代价是需要支付λT1a(p1)和(p1)的费用。参考文献[4]中对收益函数的定义,定义用户1的收益函数为

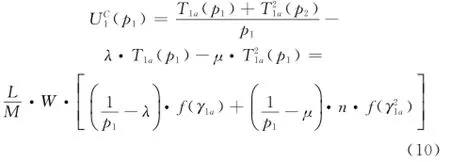
该定义不同于文献[2]中对于用户2的补偿由接入点做出,用户1直接对用户2进行价格补偿。

同理,用户2的收益函数定义为

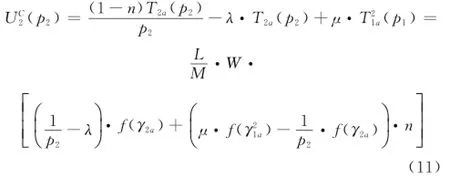
4 基于纳什谈判解的最优激励算法

本节将采用合作博弈理论中的纳什谈判方法对图1所描述的系统进行分析,并得到源节点的最优激励价格。

4.1 纳什谈判解的基本概念和定理

定义1 合作博弈论中的谈判问题可以定义为:设k=1,2,…,K,K表示博弈参与者的集合,表示一个非空的闭合凸子集,用来表示参与者所有可行解的收益分配集合。令¯Ui为第i个参与者所期望得到的最小支付。(S,¯Ui)被称为一个有K个参与者的谈判问题。如果S满足纳什提出的4条公理,并且这个解[13]满足:

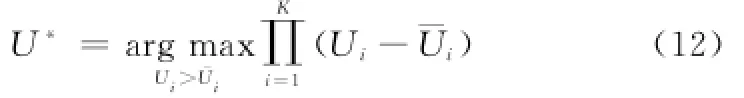
这个解被称为“纳什谈判解”(Nash bargaining solution,NBS)。“NBS”的意义为:K个参与人选择一个策略使得他们收益增益的乘积最大,这个乘积也称为“纳什乘积”。

定理1 在协作带宽一定的条件下,本文提出的激励问题为纳什谈判问题。

证明两个用户的可行收益分配集合为

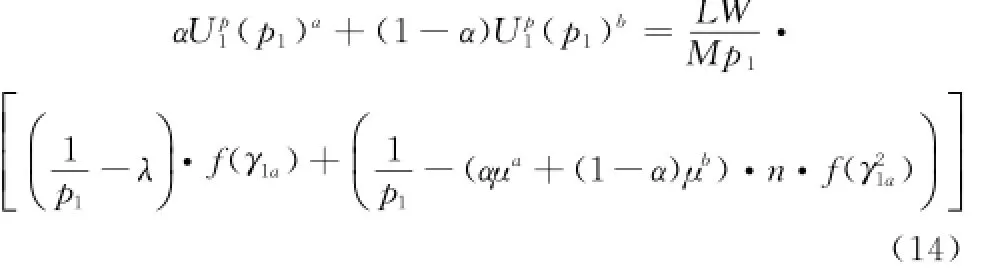
因此只需证明μ为凸子集,因为μ是全体实数集合,又因为整个欧式空间n为凸集,所以μ为凸子集,即αμa+ (1-α)μb∈μ。由此可以证明αUp1(p1)a+(1-α)Up1(p1)b∈S1,同样可以证明αUp2(p2)a+(1-α)Up2(p2)b∈S2。从而本文提出最优激励问题可以采用纳什谈判方法进行解决。证毕

4.2 基于NBS的最优价格

根据纳什谈判方法,前文所描述问题的NBS的表示方式为

式(20)可以决定源节点和中继节点何时进行合作:当式(20)取值大于零,且UC1(p1)-U1(p1)和UC2(p2)-U2(p2)的值也同时大于零时,源节点和中继节点可以达成合作。即,和非合作方式相比,在合作中源节点和中继节点的效用均得到了提高,合作有利可图。

定理2 针对图1所提的系统,当用户1的发射功率为p1,用户2的发射功率为p2,且用户1和用户2的合作收益为UC1(p1)和UC2(p2),不合作收益为U1(p1)和U2(p2)时,则(UC1(p1)-U1(p1))(UC2(p2)-U2(p2))最优价格的NBS如式(21)所示:

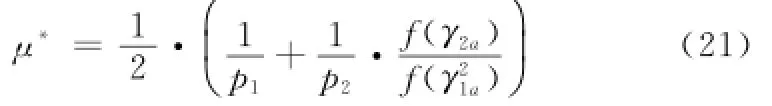
基于以上分析,本文提出了一种基于NBS的最优激励协作算法,具体过程如下。

算法1 基于NBS的最优激励算法

(1)用户1和用户2交换彼此发射功率信息p1和p2。

(2)用户1根据式(21)计算最优激励价格并通知给用户2。

(3)用户2判断UC2(p2)-U2(p2)的值。

①如果UC( p)-U(p)＞0,则用户2合作并将合作

2222信息反馈给用户1。

②否则,用户1终止合作。否则,用户2不合作。

(4)用户1根据用户2的反馈信息,判断UC1(p1)-U1(p1)的值。

①如果UC1(p1)-U1(p1)＞0,则用户1发送数据给用2。

算法1的实现前提是用户1和用户2需要获知信噪比信息γ1a、γ12和γ2a。

5 基于粒子群优化的转发功率算法

在得到用户1的最优价格μ*之后,用户2的合作增益效用可以表示为

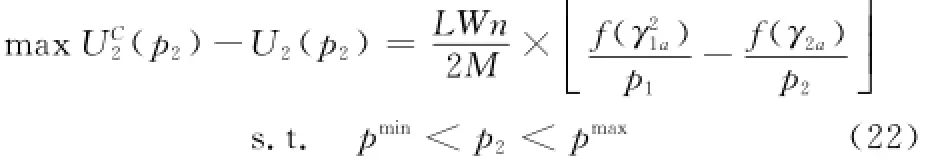
由式(22)可以看出,当用户2获知用户1的最优出价μ*后,用户2希望最大化其合作增益效用,用户2的合作增益效用依赖于效率函数和自身的发射功率,同时效率函数

f(γ2

1a)和f(γ2a)是p2的函数,因此用户2的转发功率决定了其合作增益效用,但f(γ21a)和f(γ2a)中含有e的指数项,故式(22)很难求得闭合解。为了获得中继节点的最优转发功率,本文提出了一种基于粒子群优化的最优转发功率算法。

粒子群优化算法(particle swarm optimization,PSO)是由文献[14]提出的一种进化计算技术。PSO算法首先在可行解空间中随机初始化一群粒子,每个粒子代表优化问题的一个潜在解,并用位置、速度和适应度值表示该粒子的特征,适应度值由适应度函数计算得到,其值的大小代表了粒子的优劣。粒子在可行解空间中运动,通过跟踪个体极值和群体极值更新个体位置,个体极值是指个体所经历的位置中计算得到的适应度值最优的位置,群体极值是指所有粒子搜索得到的适应度值最优的位置。粒子每更新一次位置,就计算一次适应度值,并通过比较新得到适应度值和个体极值、群体极值的使用度值更新个体极值和群体极值的位置。

为求解式(22)所提出的优化问题,设适应度函数为fitness(p2)=U2(p2)-UC2(p2)。问题转换为求解:

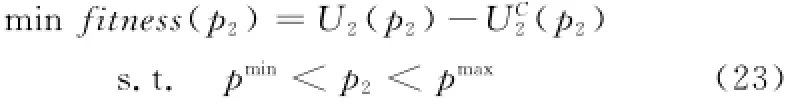
设种群的粒子数为M,种群的位置为Pj(j=1,2,…, M),其搜索空间为[pmin,pmax],粒子速度为Vj,fitness(Pj)为潜在解的适应度值,pbest和gbest分别为最优个体位置和最优全局位置。本文提出的基于粒子群优化的转发功率算法如下。

算法2 基于粒子群优化的转发功率算法

(1)随机初始化种群的位置Pj,Pj～f(pmin,pmax),其中f(·)为均匀分布函数,pmin和pmax分别为最小和最大发射功率。

(2)随机初始化粒子的速度Vj,Vj～f(0,1)。

(3)初始化第j个粒子的最优位置:pbest←Pj,如果fitness(pbest)＞fitness(gbest),更新种群的最优位置:gbest←pbest。

(4)初始化r1、r2,ri(i=1,2)～f(0,1)。

(5)按下式更新粒子的速度和位置:

①Vj←w Vj+c1r1(pbest-Pj)+c2r2(gbest-Pj),其中w为惯性权重,c1、c2为学习因子。

②Pj←Pj+Vj

③如果fitness(Pj)＜fitness(pbest),更新粒子的最优位置pbest←Pj;如果fitness(pbest)＜fitness(gbest),更新粒子群的最优位置gbest←pbest。

(6)若满足停止条件(运算精度或迭代次数),搜索停止,则gbest为最优解。

(7)否则,返回步骤5继续搜索。

由于式(22)是γ21a和γ2a的函数,因此用户2需要知道信道的信噪比状态信息γ21a和γ2a。

6 实验结果及分析

仿真模型参考文献[15],具体如图2所示。

图2 仿真模型

假设接入点在原点的位置上,用户1位于X轴正方向900 m处,即用户1的坐标为(900,0)。用户2的位置在X轴的方向移动,其坐标为(d,0)。d为用户2到接入点之间的距离,仿真中的参数设置如表1所示。

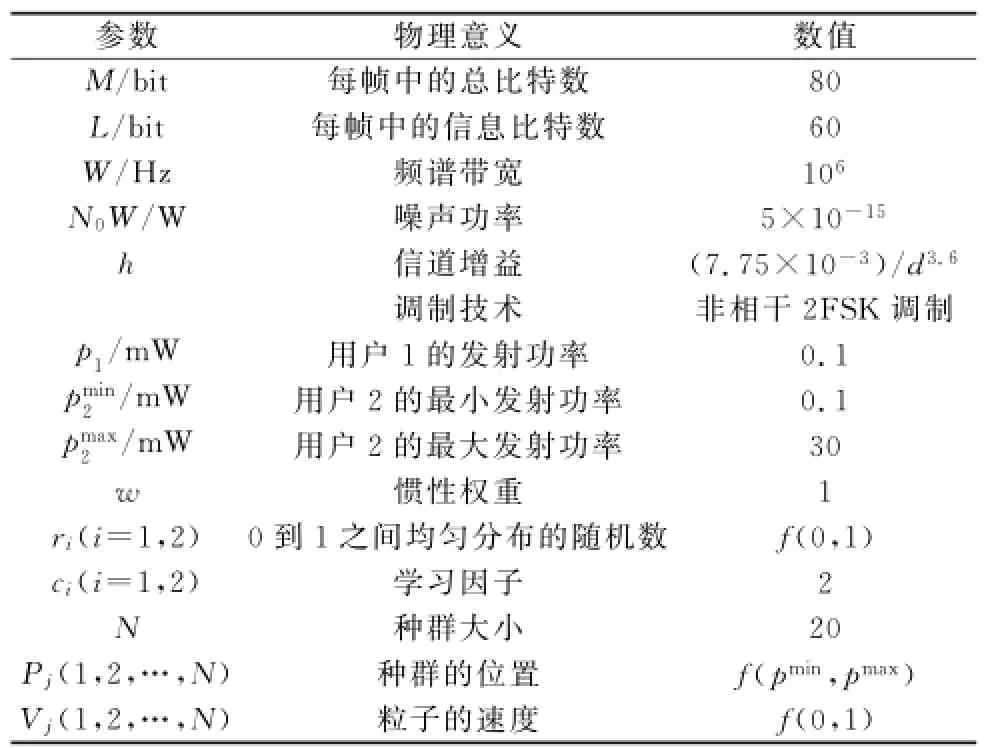
表1 仿真参数

在图3中,纵轴表示两个用户的收益增益乘积((UC1(p1)-U1(p1))(UC2(p2)-U2(p2)))的值,横轴表示用户2距离接入点的距离,其负值表示用户2在接入点左侧,正值表示用户2在接入点右侧。

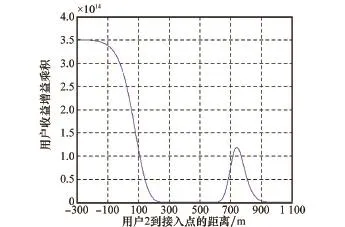
图3 用户的收益增益乘积

从图3中可以看出,当用户2距离接入点的距离小于260 m或在600～1 000 m时,双方的收益增益乘积为正,由图4同时可以看出,当用户2距离接入点的距离小于260 m时,用户1和用户2合作时的收益小于不合作时的收益,因此,只有当用户2距离接入点在600～1 000 m时(此时,UC( p)

11-U1(p1)＞0且UC2(p2)-U2(p2)＞0),用户1和用户2通过合作可以增加彼此的收益,故此距离为协作距离。

由图4可以看出,在协作距离内,和不合作相比,用户1和用户2的收益都明显增加。图4中,用户1不合作时的收益之所以接近于0,是因为仿真将用户1距离接入点的距离设置的较远,其信道条件较差,这更体现出用户1需要其他用户协作其传输。

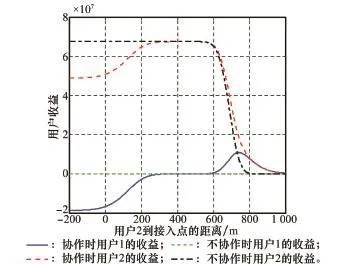
图4 协作与不协作时用户的收益

图5给出了用户1协作时的收益、能量效率及不合作时的能量效率,从图5中可以看出,用户1的收益曲线包含于能量曲线。因此,在协作距离内总能保证用户1能量效率的提升,同时由图5也可以看出,和不合作相比,用户1的能量效率有了明显的提升。

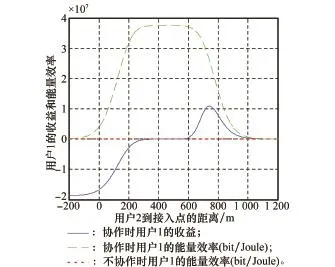
图5 用户1的收益和能量效率

图6给出了用户1采用纳什谈判价格和随机价格时两个用户的收益增益乘积,由图6可以看出,当用户1采用随机价格时,两个用户的收益增益乘积在协作距离内不能始终为正,如果达成合作,一方的得益是以另一方的损失为前提的,因此当用户1采取随机价格激励时,不能总是促使合作,并且即使收益增益乘积为正,和本文提出的最优出价相比其值也不保证一定最优。

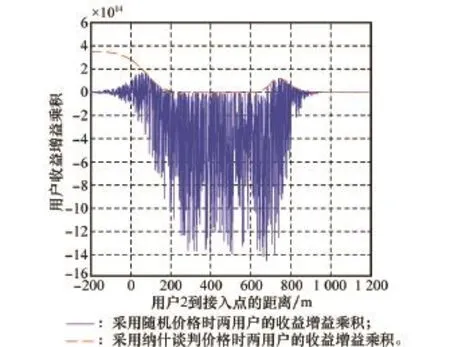
图6 用户的收益增益乘积

图7给出了当用户1采取随机价格激励时用户1和用户2的收益,从图7中可以看出两个用户的收益函数是随机变化的,和图4中的最优价格激励相比,在协作距离内,两个用户的收益不能达到最优。

图8给出了在协作距离为750 m、800 m和850 m时,适应度值和迭代次数的关系。从图8中可以看出,当迭代次数大于50次时适应度值(即用户2的合作收益增益)在搜索空间内收敛,其收敛速度较快,对于目前的终端计算能量来讲是可以完成此计算任务的。

图9给出了当用户2采取不同转发功率时用户1在不同协作距离的能量效率。由图9可以看出,本文所提NGPSO算法和用户2的转发功率为0.1 mW时相比显著的增加了用户1的能量效率,但同时也可看出,和用户2的转发功率为0.2 mW时相比,能量效率提升并不明显,这是因为当用户2的转发功率达到一定值时,用户1到达接入点的有效数据量已经基本稳定,因此即使用户2增加转发功率也不会明显改善用户1的能量效率。

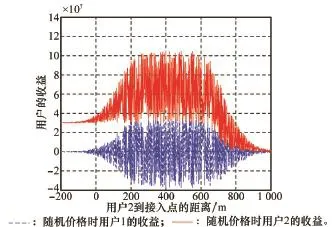
图7 随机价格时用户的收益

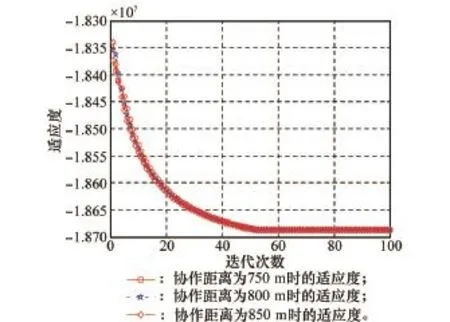
图8 适应度和迭代次数

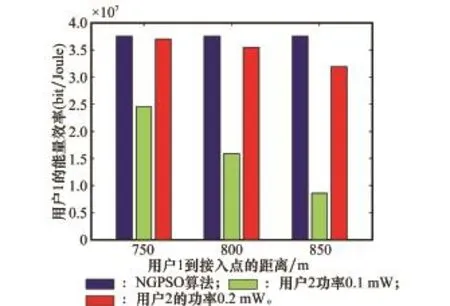
图9 用户1的能量效率

图10给出了当用户2采取不同转发功率时其收益在不同协作距离的变化情况。由图10可以看出本文所提方法和采用固定功率转发相比,用户2的收益有了显著的提升。

图11给出了系统总的能量效率采用NGPSO算法和固定功率转发在不同协作距离时的变化情况。从图11中可以看出,和用户2的转发功率为0.1 mW或0.2 mW时相比,本文所提的NGPSO算法的能量效率不是很高,这是因为为了说明本文所提算法收敛速度较快,将用户2的最大转发功率设置为用户1的300倍增大了搜索空间,当用户2的转发功率大到一定程度时,其对有效数据量的提升并不能带来明显好处,反而降低了能量效率,在实际应用当中二者的功率差距不会如此之大。当用户2的转发为0.2 mW时,和0.1 mW相比系统总的能量效率有显著的提升,因此,适当减少用户2的搜索空间时,可以改善系统的能量效率。同时,本文所提算法第二阶段的优化目标为用户2的合作收益增益,如果考虑系统总的能量效率,可以对式(22)的目标函数进行改进,进行联合优化,也可以提升系统总的能量效率,这是下一步的工作。

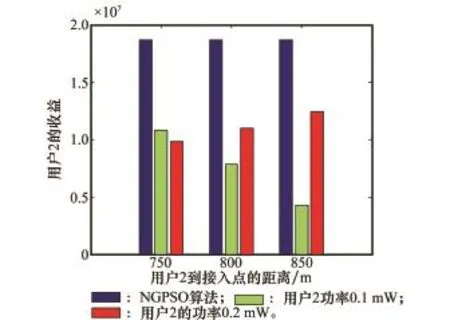
图10 用户2的收益

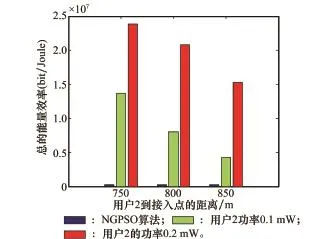
图11 总的能量效率

7 结论

为促使Ad-hoc网络中的“自私”节点进行合作,本文提出了一种NGPSO算法,通过源节点对中继节点转发的数据进行价格补偿,使中继节点协助源节点进行数据传输。首先,将源节点的最优出价归结为纳什谈判问题,得到具有帕累托最优性的激励价格的纳什均衡解,从而保证源节点和中继节点在合作中皆可获得最佳收益;之后,在获得源节点的出价后,通过粒子群优化算法中继节点决定其转发功率,使其合作收益增益最大。仿真实验表明,本文所提NGPSO算法,和随机价格激励相比,能使源节点和中继节点在合作中获得的收益达到最优;和中继节点固定转发功率相比,能明显提高中继节点的收益和源节点的能量效率;同时,适当设置中继节点的功率搜索范围,可以保证系统总的能量效率。

[1]Marti S,Giuli T,Lai K,et al.Mitigating routing misbehavior in mobile Ad hoc networks[C]∥Proc.of the IEEE International Conference on Mobile Computing and Networking,2000:255-265.

[2]Srinivasan V,Nuggehalli P,Chiasserini CF,et al.An analytical approach to the study of cooperation in wireless ad hoc networks[J]. IEEE Trans.Wireless Communications,2005,4(2):722-733.

[3]Felegyhazi M,Hubaux J P,Buttyan L.Nash equilibria of packet forwarding strategies in wireless Ad hoc networks[J].IEEE Trans.on Mobile Computingation,2006,5(5):463 476.

[4]Ileri O,Mau S C,Mandayam N B.Pricing for enabling forwarding in self-configuring Ad hoc networks[J].IEEE Journal on Selected Areas Communications,2005,23(1):151-162.

[5]Shastry N,Adve R S.Stimulating cooperative diversity in wireless ad hoc networks through pricing[C]∥Proc.of the IEEE International Conference on Communications,2006:3747-3752.

[6]Cong L,Zhao L,Zhang H,et al.Pricing-based game for spectrum allocation in multi-relay cooperative transmission networks[J].IET Communications,2011,5(4):563-573.

[7]Zhang G,Yang K,Ding E,et al.Fair and efficient resource sharing for selfish cooperative communication networks using cooperative game theory[C]∥Proc.of the IEEE International Conference on Communications,2011:1-5.

[8]Zhang G,Yang K,Liu P,et al.Joint channel bandwidth and power

allocation game for selfish cooperative relaying networks[J].IEEE Trans.on Vehicular Technology,2012,61(9):4142-4156. [9]Zhang G,Yang K,Liu P,et al.Resource-exchange based cooperation stimulating mechanism for wireless ad hoc networks[C]∥Proc. of the IEEE International Conference on Communications,2012:297 -301.

[10]Goodman D J,Mandayam N B.Power control for wireless data[J]. IEEE Personal.Communications,2000,7(2):48-54.

[11]Saraydar C U,Mandayam N B,Goodman D J.Pricing and power control in a multicell wireless data network[J].IEEE Journal on Selected Areas Communications,2001,19(10): 1883-1892.

[12]Krikidis I,Thompson J,Mclaughlin S.et al.Amplify-and-forward with partial relay selection[J].IEEE Communications Letters,2008,12(4):235-238.

[13]Nash J.The bargaining problem[J].Econometrica,1950,28 (2):155-162.

[14]Kennedy J,Eberhart R.Particle swarm optimization[C]∥Proc.of the IEEE International Conference on Neural Networks, 1995:1942-1948.

[15]Zhang Z,Shi J,Chen H,et al.A cooperation strategy based on Nash bargaining solution in cooperative relay networks[J]. IEEE Trans.on Vehicular Technology,2008,57(4):2570- 2577.

Cooperation algorithm based on game theory and particle swarm optimization for Ad-hoc networks

ZHANG Chuang,ZHANG Jia-yan,ZHAO Hong-lin
(Communication Research Center,Harbin Institute of Technology,Harbin 150080,China)

To stimulate the selfish nodes of Ad-hoc networks to participate in cooperation,a cooperation algorithm based on Nash Bargaining of game theory and particle swarm optimization(NGPSO)is proposed.In the first stage of the proposed algorithm,the relay node is paid by the source node for forwarding source nodes’data,then cooperation between the source node and the relay node can be reached.We model the optimal bid of the source node as Nash bargain,and Nash equilibrium of the optimal bid which is Pareto efficient is given. Consequently,the optimal bid can guarantee that the source node and the relay node obtain optimal revenue.In the second stage of the proposed algorithm,after obtaining the optimal bid of the source node,the relay node determines optimal transmit power through particle swarm optimization to maximize its own cooperative gain. Simulation results show that,compared to random price incentive mechanisms,the NGPSO algorithm can make the source node and the relay node obtain optimal revenue.Meanwhile,the proposed algorithm improves the cooperative gain of the relay node and the energy efficiency of the source node compared to the algorithm where the relay node uses constant transmit power.Furthermore,when the relay node appropriately sets its search space, the total energy efficiency of the whole system can be ensured.

cooperation algorithm;game theory;particle swarm optimization;energy efficiency

TP 393.01

10.3969/j.issn.1001-506X.2015.03.30

张闯(1986-),男,博士研究生,主要研究方向为协作通信、链路自适应传输。

E-mail:cangshanerhai@126.com

张佳岩(1974-),男,讲师,博士,主要研究方向为抗干扰通信技术、协作通信。

E-mail:JYzhang@hit.edu.cn

赵洪林(1969-),男,教授,博士研究生导师,主要研究方向为扩频通信、软件无线电技术和宽带无线通信网络研究。

E-mail:hlzhao@hit.edu.cn

网址:www.sys-ele.com

1001-506X(2015)03-0664-07

2013 12 06;