基于Laguerre图的自优化A-Star无人机航路规划算法

2015-06-05魏瑞轩许卓凡王树磊吕明海

系统工程与电子技术 2015年3期

关键词：航路交点威胁

魏瑞轩,许卓凡,王树磊,吕明海

(空军工程大学航空航天工程学院,陕西西安710038)

基于Laguerre图的自优化A-Star无人机航路规划算法

魏瑞轩,许卓凡,王树磊,吕明海

(空军工程大学航空航天工程学院,陕西西安710038)

为了降低无人机航路规划的运算量,减少规划时间,确保算法对于任意形状威胁区域和地形的适应性以及所规划航路的准确性,提出了一种新颖的LA-Star算法用于无人机航路规划。首先把威胁区域和禁飞区域简化为圆形,利用Laguerre图算法进行航路预规划,在此基础上简化二次规划空间的范围,之后恢复威胁区域和禁飞区域的真实形状,在简化后的规划空间内使用改进A-Star算法实施二次航路规划,最后对生成的航路进行自优化处理。仿真结果证明了LA-Star算法满足航路规划的实时性和准确性要求。

无人机;航路规划;LA-Star算法;Laguerre图;A-Star算法

0 引言

随着现代科学技术的进步和发展,未来战场上以多架无人机(unmanned aerial vehicle,UAV)协同的方式执行各类任务将成为一种重要的作战方式[1]。航路规划作为无人机任务规划的重要组成部分之一,主要是依据地形和敌方火力威胁信息,在一定约束条件下,寻找从起点到目标点的可行航路[2]。在航路规划问题中,常用的规划算法包括AStar算法[3]、Dijkstra算法[4]、Voronoi图算法[5]、Laguerre图算法[6]、遗传算法[7]、粒子群优化算法[8]、蚁群算法[9]等。

基于图形(Graph-based)的航路规划算法由于空间复杂度和时间复杂度比较小、结构简单等特点受到了广泛的关注[10-11],Laguerre图就是其中的典型代表。文献[6]针对目前Laguerre图生成算法不易实现的问题,提出了一种基于Delaunay图的Laguerre图构造算法,其时间复杂度为线性对数阶,运行时间能够满足在线规划的要求。但是由于Laguerre图方便解决关于圆的几何问题[12],因此使用Laguerre图进行无人机航路规划就必须把威胁区域(为了方便,本文中威胁区域和禁飞区域统一称为威胁区域)简化为二维平面上的一组圆,圆心坐标和圆的半径分别代表威胁区域的位置以及威胁半径,而对于大多数威胁区域不是圆形的情况Laguerre图就无法进行准确航路规划。A-Star算法是一种启发式的图搜索算法[13],可以在威胁区域是任意形状的情况下进行航路规划,但是由于算法较为复杂,时间复杂度较高,不易满足实时规划的要求[14]。

为了解决算法实时性和准确性之间的矛盾,本文首先对A-Star算法进行了改进,提出了自优化A-Star算法,然后在此基础上提出了基于Laguerre图的自优化A-Star算法,即LA-Star算法。保证了航路规划的实时性以及对任意形状威胁区域的适用性。

1 自优化A-Star算法基本原理

1.1 A-Star算法

A-Star算法是一种启发式的图搜索算法,能够在具有多约束条件以及任意形状的威胁环境下进行航路规划[13]。它的关键思想是选择合适的启发函数,对于各个扩展节点的代价值进行计算和评估,从而选择代价值最优的结点加以扩展,直到找到目标节点为止。

在A-Star算法需要建立两个列表:open表和close表, open表用于存放经过推算但是还没有扩展过的节点,close表用于存放已经被扩展过的节点。对于被扩展的节点需要进行代价评估,这需要构造代价函数,其一般形式如下:

式中,g(n)是指无人机从起始节点Start运动到节点n已经消耗的代价;h(n)是指从节点n运用到目标节点Target估计需要消耗的代价;f(n)作为决定航路点拓展问题的关键信息,其形式一般根据实际问题的特点和需要决定[15]。

本文中g(n)用从初始节点Start到节点n所规划航路的长度表示,h(n)用节点n到目标节点Target的欧氏距离表示。

1.2 威胁区域的规避

判断A-Star算法拓展节点是否在威胁区域范围以内,本文采用“射线判断法”,如图1所示,判断点P(xn,yn)是否在多边形威胁区域以内,则以P点为起点做如下射线:

判断该射线与威胁区域边界交点的个数,若交点数为奇数,则判断Pn点在威胁区域内,若交点数为偶数,则判断Pn点在威胁区域外。在图1中,点P2引出的射线与威胁区域边界存在1个交点,因此在威胁区域内,而点P1、P3、P4分别存在0、0、2个交点,因此在威胁区域以外。

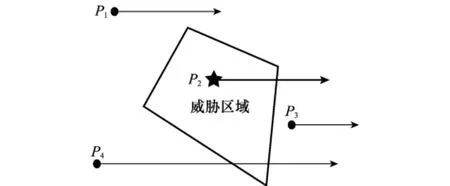
图1 判断拓展节点所在区域

在搜索拓展节点的时候,通过判断节点是否在威胁区域内来约束节点的拓展,不拓展在威胁区域内的节点,也就是在航路规划空间内将威胁区域排除,从而进一步缩小了搜索空间,提高了搜索效率。

在规划空间内排除了威胁区域后,拓展新节点要分两种情况讨论,假设节点Pn-2和Pn-1已经被拓展,下一步需要拓展节点Pn,如图2所示,那么只需要判断Pn-1与Pn的连线与威胁区域的边界是否存在交点,图中Pn-1P'n的连线与威胁区域存在两个交点,因此P'n要排除,而Pn-1Pn的连线与威胁区域不存在交点,因此Pn是合适的拓展节点。

图2 节点拓展时的两种情况

1.3 进入角约束

由于任务需要,无人机在到达目标点之后需要按照一定的航向角接近目标[16],因此在目标点周围设置了虚拟威胁区域,这样一方面控制了无人机的进入角度,另一方面压缩了算法的搜索空间,从而提高了效率,虚拟威胁区域的设置如图3所示。

图3 设置虚拟威胁区域

1.4 航路点自优化

A-Star算法所规划的航路存在航向变化频繁且航路点过于密集的特征,不适合直接应用于无人机飞行[17]。因此对所规划的航路点进行优化是十分有必要的。这里提出一种在已规划航路基础上删除、插入航路点的优化算法。

1.4.1 航路点的删除

定义2 Ni可优化:如图4所示,依次连接NiNi+kNi+k+1(k=1,2,3…),若连线互相没有交点,则称可连,否则称不可连。若k＜K+1时NiNi+kNi+k+1可连,k=K+1时NiNi+kNi+k+1不可连,则可以连续删除航路点Ni+k(k= 1,2,…,K),同时将NK后续航路点的下标减去K。航路点的删除优化从起点到终点依次顺序进行。

图4 删除多余的航路点

1.4.2 航路点的插入

经过航路点删除后,仍然可以实施进一步优化,在航路点之间插入一些新的节点,再根据定义2进行反向顺序点优化。

航路点插入的流程如下,在生成航路上的两个连续航路点连线上等间距地插入若干个新航路点。如图5所示,初始生成的航路为ABCD,在连续航路点之间插入新的航路点后再进行反向顺序点优化,得到更优的航路AA4C1D。

图5 插入航路点优化航路

2 LA-Star算法原理及实现

2.1 Laguerre图航路规划基本原理

Laguerre图是Voronoi图的衍生图,非常适合用于解决涉及圆的几何问题[12]。引入Laguerre图用于UAV的航路规划,其生成元为平面上的一组圆,圆心和半径分别表示威胁源的位置及覆盖范围等信息,若两个威胁区域不相交,Laguerre图总能够找到一条合适的路径避开威胁源的攻击范围[6]。

使用Laguerre图进行无人机航路规划首先需要假设每个威胁区域为圆形,其次在任务空间内根据各个威胁区域的位置和半径画出Laguerre图,最后便可以通过对Laguerre图各个路径代价的分析得到合适的无人机航路。

2.2 Laguerre图算法优化

为了优化生成的路径,本文在使用Laguerre图规划之前在地图边缘上增加了若干虚拟威胁源,这样使得生成的Laguerre图路径分布更加均匀,更加适合无人机飞行。如图6所示,虚拟威胁源用深色小圆表示。

图6 增加虚拟威胁源

2.3 威胁区域简化

对于威胁区域简化,采用“外切圆法”,即无论威胁区域是什么形状,只取一个半径尽可能小的圆与威胁区域外切,把威胁区域全部包含在内,这样就把威胁区域简化成为了圆形,如图7所示。

探究1 在其他条件不变的情况下，点(为表达方便，以下讨论中统称该点为D)是否可以换成y轴上的其他点(0,b)呢？

图7 简化威胁区域

2.4 缩小自优化A-Star算法规划范围

在使用自优化A-Star算法进行二次规划之前,需要对规划空间进行简化,以缩减算法的搜索空间,这也是LAStar算法的关键之一。在这里提出一种根据已有航路点简化规划区域的算法:

步骤1 连接NiNi+1并延长,若与第一次所规划的航路没有交点则NiNi+1为所简化区域的一条边。

步骤2 若NiNi+1的延长线与第一次所规划的航路存在交点,则依次连接NiNi+k(k=1,2,3…),当0≤k≤q时,NiNi+k与Ni+mNi+n(0≤m,n≤q且m≠n)不相交,当k=q+1时,NiNi+q+1与Ni+qNi+q+1相交,则NiNi+q为所简化区域的一条边。

步骤3 根据第一次规划的航路从起点开始按照顺时针或者逆时针方向对规划空间进行简化,直到首尾连接形成简化的多边形区域。

2.5 LA-Star算法基本流程及创新性

LA-Star算法的基本流程如图8所示。

图8 LA-Star算法流程

LA-Star算法的创新有以下几点:一是对于传统A-Star算法的改进,包括改进了威胁区域的规避方法、利用虚拟威胁区域增加了无人机进入角约束以及增加了航路点自优化的过程;二是对Laguerre图算法的优化,即增加虚拟威胁源以优化生成的航路;三是对于任意形状威胁源的处理可以简化成圆形区域的思想以及两种规划算法的结合。

3 算法仿真与性能分析

现假设任务区域为一个大小为100 km×75 km的二维区域,加入位置和形状随机产生的10个四边形威胁区域,任务需要两架完全相同的无人机从两个初始位置(单位: km)Start1(9.527,40.765)和Start2(14.975,50.075)分别飞往两个目标位置Target1(91.056,46.599)和Target2 (82.095,61.907),“■”点表示无人机初始位置;“◆”点表示目标点,如图9所示。下面使用LA-Star算法进行航路规划。

图9 航路规划区域

根据“外切圆法”计算出每一个多边形威胁区域的外切圆,经过简化后的威胁区域如图10所示。

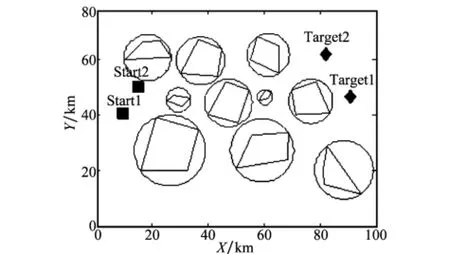
图10 经过简化的航路规划区域

对于简化后的威胁区域使用Laguerre图算法进行航路规划,得到的航路如图11中粗实线所示。

图11 Laguerre图算法规划结果

取消威胁区域的简化,即使用威胁区域的真实形状代替之前简化的圆形,如图12所示。对比看出,第一步中使用Laguerre图进行航路规划后,所规划的航路对于简化的威胁区域来说效果较好,但是在恢复威胁区域真实形状后,第一步中所规划的航路就明显不符合航路规划要求,因此需要进一步规划。接下来的任务就是简化任务区域,使用自优化A-Star算法进行航路规划。

图12 恢复威胁区域形状后的任务空间

经过计算,所得到的二次规划区域如图13中深灰色区域所示。

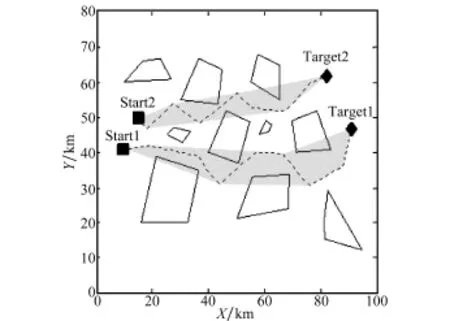
图13 简化后的航路规划区域

简化后的空间内使用自优化A-Star算法进行航路规划,所得到的航路如图14中实线所示。

图14 LA-Star算法规划的航路

3.2 数据分析与结论

对同样条件下的任务区域分别使用LA-Star算法、A-Star算法以及Laguerre图算法进行航路规划,比较它们的规划时间以及路径长度,结果如表1和表2所示。

表1 3种航路规划算法规划时间比较_

表2 3种航路规划算法规划路径长度比较__

从表1和表2的数据可以看出,在规划时间上, Laguerre图算法用时最少,LA-Star算法其次,A-Star算法用时最多且比其他两种算法大很多。这是由于LA-Star算法是在Laguerre图算法的基础上使用了自优化A-Star算法进行了精确规划,因此用时略长于Laguerre图算法,但是用时明显少于A-Star算法。

在航路长度上,Laguerre图算法规划的航路最长,LAStar算法和A-Star算法所规划的长度相同,且明显短于Laguerre图算法,这是由于使用威胁区域的原始形状使得规划的航路准确性更高。

综合分析规划时间和航路长度两组数据,可以得出结论:Laguerre图算法虽然用时最短,但是所规划的航路长度明显大于另外两种算法,且航路较为弯曲,不适合在威胁区域为非圆形的情况下使用,A-Star算法虽然路径长度较优,但是规划用时过长,不符合实时性要求。而LA-Star的规划时间略大于Laguerre图算法,但是其规划的航路长度最小,路径更优,同时符合实时性和准确性的要求。

3.3 算法快速性分析

保证其他试验条件不变,分别比较LA-Star算法、AStar算法、Laguerre图算法以及Voronoi图算法在不同威胁源个数情况下的运行时间,实验结果如图15所示。

图15 LA-Star算法比较分析

根据文献[6],Laguerre图算法的复杂度为O(n log n), A-Star算法的复杂度为O(n2),由结果分析可得,当威胁源个数较小的时候,LA-Star算法、Laguerre图算法以及Voronoi图算法的运行时间相差不大,其中Laguerre图算法的快速性最好,当威胁源数目增加,3种算法的差距逐渐增大,然而相比以上3种算法,A-Star算法的运行时间始终较长,并且相差的时间迅速增大。因此,这4种算法的快速性从优到差的顺序为:Laguerre图算法＞Voronoi图算法＞LA-Star算法＞A-Star算法。

通过实验仿真可以得出以下结论:综合LA-Star算法的快速性和准确性,其明显优于其余3种算法。

4 结束语

由Laguerre图算法和自优化A-Star算法结合的LAStar算法能够很好地解决无人机航路规划中的实时性问题和准确性问题,对现有的无人机航路规划发展具有显著的意义。然而,本算法仍有待完善之处,比如多架无人机协同的情况以及无人机初始位置和目标位置在威胁区域内的情况,这也将在后续的论文中进行研究与完善。

[1]Wei R X,Li X R.UAV system and operational use[M].Beijing:National Defense Industry Press,2009.(魏瑞轩,李学仁.无人机系统及作战使用[M].北京:国防工业出版社,2009.)

[2]Gao H,Chen X,Xia Y C.Research on UAV path planning[J]. Journal of Nanjing University of Aeronautics and Astronautics,2001,33(2):135 138.(高晖,陈欣,夏云程.无人机航路规划研究[J].南京航空航天大学学报,2001,33(2):135 -138.)

[3]Yao J F,Lin C,Xie X B,et al.Path planning for virtual human motion using improved A*star algorithm[C]∥Proc.of the 7th International Conference on Information Technology:New Generations,2010:1154-1158.

[4]Kang H,Lee B,Kim K.Path planning algorithm using the particle swarm optimization and the improved dijkstra algorithm[C]∥Proc.of the Pacific-Asia Workshop on Computational Intelligence and Industrial Application,2008:1002-1004.

[5]Peng C,Lu X Q,Dai J Y,et al.Research of path planning method based on the improved Voronoi diagram[C]∥Proc.of the 25th Chinese Control and Decision Conference,2013:2940-2944.

[6]Wang S L,Wei R X,Shen D,et al.Construction algorithm of Laguerre diagram for path planning[J].Systems Engineering and Electronics,2013,35(3):552 556.(王树磊,魏瑞轩,沈东,等.面向航路规划的Laguerre图构造算法[J].系统工程与电子技术,2013,35(3):552-556.)

[7]Ju M Y,Cheng C W.Smooth path planning using genetic algorithms[C]∥Proc.of the 9th World Congress on Intelligent Control and Automation,2011:1103 1107.

[8]Shakiba R,Najafipour M,Salehi M E.An improved PSO-based path planning algorithm for humanoid soccer playing robots[C]∥Proc.of the 3rd Joint Conference of AI&Robotics and the 5th RoboCup Iran Open International Symposium,2013:1-6.

[9]Zhao S G,Li M.Path planning of inspection robot based on ant colony optimization algorithm[C]∥Proc.of the International Conference on Electrical and Control Engineering,2010:1474 -1477.

[10]Choi J W,Curry R E.Real-time obstacle-avoiding path planning for mobile robots[C]∥Proc.of the AIAA Conference on Guidance,Navigation,and Control,2010:216-227.

[11]Lum C W,Vagners J.A search algorithm for teams of heterogeneous agents with coverage guarantees[J].Journal of Aerospace Computing,Information,and Communication,2010,7 (1):1-28.

[12]Berg M D,Kreveld M V,Overmars M,et al.Computation geometry algorithms and application[M].3rd ed.Berlin:Springer-Verlag,2008.

[13]Qi Z,Shao Z H,Ping Y S,et al.An improved heuristic algorithm for UAV path planning in 3D environment[C]∥Proc.of the 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics,2010:258-260.

[14]Qu Y H,Pan Q,Yan J G.Flight path planning of UAV based on heuristically search and genetic algorithms[C]∥Proc.of the 31st Annual Conference of IEEE on Industial Electronics Society,2005:45-49.

[15]Li J,Sun X X.A route planning’s method for unmanned aerial vehicles based on improved A-star algorithm[J].Acta Armamentarii,2008,29(7):788-792.(李季,孙秀霞.基于改进A-Star算法的无人机航迹规划算法研究[J].兵工学报,2008,29 (7):788-792.)

[16]Pascarella D,Venticinque S,Aversa R.Agent-based design for uav mission planning[C]∥Proc.of the 8th International Conference on P 2P,Parallel,Grid,Cloud and Internet Computing,2013:76-83.

[17]Li S J.Research on UAV path planning and evaluation methodology[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012.(李素娟.无人机航路规划及评价方法研究[D].南京:南京航空航天大学自动化学院,2012.)

Self-optimization A-Star algorithm for UAV path planning based on Laguerre diagram

WEI Rui-xuan,XU Zhuo-fan,WANG Shu-lei,LÜMing-hai
(School of Aeronautics and Astronautics,Air Force Engineering University,Xi’an 710038,China)

In order to relieve the operation burden and time consume for unmanned aerial vehicle(UAV) path planning,a novel UAV path planning method named LA-Star algorithm is proposed which as well guarantees the adaption in scenarios of various threat areas and terrains.Under the roundness assumption of all threat areas and no-fly-zones,the Laguerre diagram algorithm is applied to pre-plan the flight path which largely benefits path re-plan because of shrunk operation space.With the original shape of threat areas,improved A-Star algorithm is then applied in path re-planning with reference to pre-planned path.Finally,optimize the path planned above.Simulations show the LA-Star algorithm satisfies time and veracity requirements.

unmanned aerial vehicle(UAV);path planning;LA-Star algorithm;Laguerre diagram; A-Star algorithm

V 219

10.3969/j.issn.1001-506X.2015.03.16

魏瑞轩(1968-),男,教授,博士,主要研究方向为飞行器控制理论与应用。

E-mail:rxw123@sohu.com

许卓凡(1989-),男,硕士研究生,主要研究方向为无人飞行器控制理论与应用。

E-mail:15129006715@163.com

王树磊(1983-),男,博士研究生,主要研究方向为导航、制导与控制。

E-mail:wangshulei2009@gmail.com

吕明海(1990-),男,硕士研究生,主要研究方向为无人飞行器控制理论与应用。

E-mail:lmh199001@163.com

网址:www.sys-ele.com