基于VHS分子模型的DSMC方法研究分子蒸馏气相微观特性

许松林，李 阳

(天津大学化工学院，天津 300072)

基于VHS分子模型的DSMC方法研究分子蒸馏气相微观特性

许松林，李 阳

(天津大学化工学院，天津 300072)

为了研究分子蒸馏器内气体的微观特性，基于变径硬球分子模型，采用了直接模拟蒙特卡洛方法，考虑了分子转动能和平动能，建立了描述分子蒸馏气相传递过程的一维和二维模型，计算了不同蒸发温度下的蒸发效率，并将模拟计算值与实验数据对比，验证了模型的合理性．通过模拟分子的运动和碰撞过程，分析了蒸发温度、冷凝温度和蒸发面与冷凝面的间距等参数对气相空间的碰撞频率和分子平均自由程分布的影响．结果表明：碰撞频率和平均自由程分布的变化始终呈相反趋势；在蒸发面附近，碰撞频率和分子平均自由程分别处于各自最大值和最小值；从蒸发面到冷凝面的气相空间，碰撞频率逐渐减小，分子平均自由程逐渐增大；靠近冷凝面时，碰撞频率和分子平均自由程分别达到各自最小值和最大值；随着蒸发温度或冷凝温度的升高，气相空间同一位置处的碰撞频率增大而平均自由程减小；随着蒸发面与冷凝面的间距增加，碰撞频率在同一位置处有所增大，但在冷凝面附近更小；间距增加，同一位置处的分子平均自由程减小，但是冷凝面附近，间距越大时平均自由程也越大．

分子蒸馏；直接模拟蒙特卡洛方法；变径硬球；碰撞频率；平均自由程

分子蒸馏是一种高效分离热敏性、黏滞性、高沸点性物质的技术，利用分子平均自由程的差别，在远低于物质常压沸点的温度下进行的高真空非平衡蒸馏．国内外学者对分子蒸馏的液相传递过程进行了广泛研究[1-4]，然而气相空间流动机理的分析还不够深入．由于气相空间分子间的碰撞频率对蒸馏速率和传质效率影响较大，气体分子平均自由程是分子蒸馏过程的重要参数，因此，针对分子蒸馏气相空间碰撞频率和平均自由程等微观特性的研究有着深刻的意义，可用于指导分子蒸馏器的设计与核算．

分子蒸馏器的蒸发面与冷凝面之间的距离和气体分子平均自由程为同一量阶，分子蒸馏器内气体的流动属于过渡流区域，不再满足连续介质假设，该流动过程的控制方程为Boltzmann方程．因此，研究分子蒸馏器内气体的微观特性，实质上是求解Boltzmann方程．由于Boltzmann方程是一个非线性的积分微分方程，给解析求解带来了极大困难．目前求解Boltzmann方程主要采用介观方法，已有的介观方法大体上可以分为两类．

(1)以动力学理论的Boltzmann方程为基础，通过数值求解分布函数而获得宏观流动信息．若不对其进行简化，数值求解Boltzmann方程，目前无法求得近似解；若进行简化，由于分子蒸馏气相空间的流动是一个多组分、可压缩及变温的流动，简化的Boltzmann方程对该流动过程的模拟存在较大的误差．

(2)构造新的介观流体模型，直接从流动的物理过程出发，通过模拟系统的真实物理过程，再现流动现象．其中，Bird[5]提出的直接模拟蒙特卡罗(direct simulation Monte Carlo，DSMC)方法，基于真实分子运动的物理模型，采用有限个仿真分子代替真实气体分子，使计算量大大减小；而且，充分考察分子的运动和碰撞过程，高效地反映气体分子运动的微观特性，成为过渡领域应用比较广泛的介观模拟方法之一．至今已有许多学者采用DSMC方法对分子蒸馏气相传递过程进行了模拟研究．

Bhandarkar等[6]首次采用DSMC方法研究了分子蒸馏器内气体的宏观和微观性质，并与Hickman等[7]实验方法得到的结果进行了对比分析．Lutišan等[8]基于硬球(hard sphere，HS)分子模型，应用DSMC方法对分子蒸馏过程中单组分体系的蒸发和冷凝进行了研究，给出了气相空间单一组分气体分子的碰撞频率和平均自由程等微观性质分布规律，考察了操作参数、结构参数对其分布的影响，还分析了碰撞频率对传质效率的影响．然而，上述模型研究都是基于理想蒸发速率的前提展开的，即认为所有逸出蒸发面的蒸汽分子无论经过多少次碰撞最终都到达了冷凝面．而实际过程中，由蒸发面逸出的蒸汽分子在气相空间存在碰撞，导致部分分子返回蒸发面，从而实际蒸发速率小于理论蒸发速率，即气相传递过程的非理想性．Batistella等[9]考虑了这一非理想性因素，通过DSMC方法用HS分子模型对单组分体系的气体分子碰撞和运动进行了模拟计算，探讨了分子蒸馏器内气相传递过程的非理想性对气体宏观和微观性质分布的影响．由于实际待分离的物质多为多原子气体分子，多原子气体分子除了具有分子平动能之外，还有分子转动能和振动能．但是，分子振动的特征温度很高，分子蒸馏的实际操作温度下不足以激发分子的振动能，故在模型中忽略分子的振动能是合理的．因此，在考虑分子平动能的基础上，Hu 等[10]同时考虑了分子的转动能，应用DSMC方法，选择HS分子模型，建立了新的计算模型，重点研究了新模型下分子蒸馏器内气体分子宏观性质分布的改变，及操作参数、结构参数对分子蒸馏过程的影响．总之，上述文献均采用HS分子模型对分子蒸馏器内气体的流动过程进行了模拟研究，该分子模型具有固定不变的碰撞截面，而真实气体分子的碰撞截面是随着碰撞对相对速度增大而减小的，HS模型导致模拟中黏性系数和温度的关系与真实气体存在一定的偏差．对此，Bird[5]引入了变径硬球(variable hard sphere，VHS)分子模型．VHS模型的分子具有HS模型分子一样的均匀的散射几率，但它的碰撞截面是分子间相对速度的函数，与真实气体分子碰撞情况更吻合，在模拟气体分子碰撞等方面具有明显的优越性．同时，Hu等[10]分析了分子蒸馏气相空间的流场性质分布在考虑分子转动能后的变化，结果发现考虑分子转动能的模型计算结果更接近实际情况．因此，选用更能真实反映气体碰撞的VHS模型，考虑分子的平动能和转动能，对分子蒸馏气相空间的分子碰撞进行模拟是有必要的，而且更符合实际．此外，这些研究主要探讨了单一组分气体分子的宏观或微观性质分布规律，文献[10]中虽然考察了双组分体系的气体分子蒸发和冷凝过程，但并没有给出气相空间分子微观性质分布，如总的碰撞频率和平均自由程的分布．碰撞频率和平均自由程又是反映微观过程的两个关键参数．

笔者基于VHS分子模型，采用DSMC方法，在考虑分子平动能和转动能的条件下，建立了能更好地反映分子蒸馏气相空间传递过程的新模型，模拟了分子蒸馏气相空间二元组分的运动和碰撞，给出了分子蒸馏气相空间总的碰撞频率和平均自由程等微观性质分布规律，并考察了蒸发温度和冷凝温度等操作参数和蒸发面与冷凝面的间距等结构参数对其影响．研究结果对优化操作及合理设计分子蒸馏器具有一定的指导意义．

1 模型与方法

1.1 物理模型

模拟分子蒸馏气相空间分子的运动，物理模型如图1所示，将蒸发面与冷凝面简化为两平行平板．x轴与蒸发面垂直并指向冷凝面，y、z轴沿蒸发面方向．蒸发温度为TE，冷凝温度为TC，蒸发面与冷凝面之间的距离为D．高温下，液相分子脱离蒸发面后通过气相分子间的碰撞作用，迅速向高真空区膨胀而形成气相分子蒸汽流，造成气体沿x方向发生传热、传质和动量传递，描述x方向上气体分子微观特性的各物理量也随之变化．当模拟的分子蒸馏器是同轴圆柱时，相比平行平板，气体分子运动过程中不仅位置发生了变化，方向也发生了变化．

图1 气相空间物理模型Fig.1 Physical model for the vapor space

为简化模拟计算过程，做如下假设：①分子之间只发生二元碰撞；②忽略外力场对蒸汽分子的作用；③离开蒸发面和冷凝面的蒸汽分子速度服从Maxwell分布．

1.2 计算模型

1.2.1 分子模型的选择

DSMC方法是通过模拟大量气体分子的运动与碰撞，统计仿真分子的运动状态实现对流场的模拟，因此在对流场进行模拟之前需要对分子模型进行选择．在已有的多种分子模型中，最简单、使用最广泛的是HS模型．文献[8-10]中采用的是HS模型，HS分子恒定不变的分子直径和碰撞截面简化了理论分析与模拟计算，但是HS模型与真实分子碰撞截面随分子间相对运动速度增大而减小的物理事实并不符合，在模拟分子碰撞问题时所得模拟结果与实际情况存在明显偏差．为此Bird[5]引入了VHS模型．VHS模型认为碰撞后分子的运动状态符合混沌假设，即分子散射角在整个空间方向上的分布是随机的且是均匀分布的，同时碰撞截面是碰撞对相对运动速度的函数．

引入总碰撞截面σT、碰撞分子有效直径d和相对速度ur的参考值σT,ref、dref和ur,ref，则在VHS模型中，分子直径和碰撞截面都是相对速度的函数，其定义为

式中：下标“ref”表示参考值；下标“r”表示相对值；ν为幂指数[5]．此外，该模型还给出了碰撞偏向角的定义[5]，偏向角与相对速度无关，即

式中：χ为碰撞后偏向角；b为碰撞参数．

VHS模型的分子间相互作用势是负幂律模型，即分子相互作用势()Ur是按分子中心距离r的某个负α次幂变化

式中：a为调节参数[11]；幂指数α的取值是9．

经过推导可得，VHS模型黏性系数是随温度的一定幂次变化的，这一结论比较符合真实气体规律[5]．可见，VHS模型最大限度地反映了真实气体碰撞情况，在模拟混合气体碰撞和运动方面具有优势，因此本文选择VHS模型．

1.2.2 分子模型的选择

要正确模拟非平衡流场，其关键在于能够构造出正确反映多原子分子内能状态及碰撞前后分子内能状态变化的模型[12]．本文模拟计算物系为邻苯二甲酸二异辛酯(EHP)和癸二酸二异辛酯(EHS)，相关物性参数如表1所示[13-14]．表1中A、B为Antoine 方程lg,psat＝A-B/T的系数，其中psat为饱和蒸汽压，Pa；T为液相温度，K．EHP和EHS均为多原子气体分子，分子的能量模式包括平动能、转动能和振动能．但是，由于分子振动的特征温度很高，实际分子蒸馏操作温度不足以激发工质分子的振动能量，所以，模拟计算过程中可忽略分子的振动能，只需考虑分子的平动能和转动能．统计力学证明[11]，多原子分子的平动和转动自由度均为3．

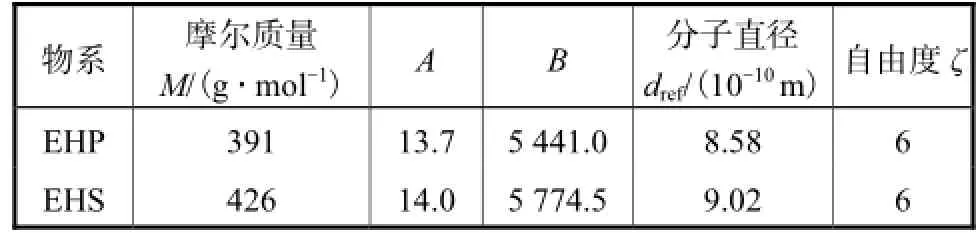
表1 EHP-EHS的物理参数Tab.1 Physical parameters of EHP-EHS

当两个气体分子碰撞时，碰撞前后的总能量是不变的．但是，总能量在平动能与转动能之间传递，导致能量的分布发生变化．对于碰撞过程中不同能量模式之间的传递及碰撞后能量的重新分布，本文采用Larsen-Borgnakke(L-B)模型来计算．L-B模型是通过随机数选择碰撞，碰撞分子对的总能量为碰撞前两分子相对平动能与转动能之和并且保持不变，然后根据总能量的平衡分布来决定每个分子碰撞后的平动能与转动能[15]．

1.3 气体微观特征量的计算

分子蒸馏器内气体流动属于高真空稀薄气体非平衡流动，通过运动和相互碰撞来实现气体分子间能量、动量的交换，而气体由非平衡态过渡到平衡态的过程，也是通过分子间的相互碰撞来实现的，因此，气体分子碰撞频率是反映微观过程的十分重要的特征量．同时，分子蒸馏的机理是以不同分子间平均自由程的差别为前提的，平均自由程也是分子蒸馏的一个关键参数．本文计算的混合气体微观特征量，主要用于计算碰撞频率和平均自由程．

1.3.1 碰撞频率

碰撞频率是指单位时间、单位体积内分子间总的碰撞次数．考虑p类分子和q类分子之间的碰撞，单位时间内p类气体分子的碰撞频率计算式[16]为

气相空间中混合气体在单位时间、单位体积内的碰撞次数，即混合气体碰撞频率的计算式[16]为

式中：s为混合气体中所有分子的种类数；pn、qn分别表示p、q类分子数密度，m-3；T,pqσ为p类分子和q类分子碰撞的有效截面，m2；r,pqu为p类分子与q类分子之间的相对速度，m/s；pf为p类气体分子的碰撞频率，s-1；Z为混合气体的碰撞频率，m-3·s-1. 1.3.2 平均自由程

由于分子运动的无规则性，一个分子在任意连续两次碰撞之间所经过的自由路程是不同的．气体分子在相邻两次碰撞之间移动的平均路程是平均自由程．一个p类气体分子的平均自由程是用它的碰撞频率去除以它的平均速度[16]，即

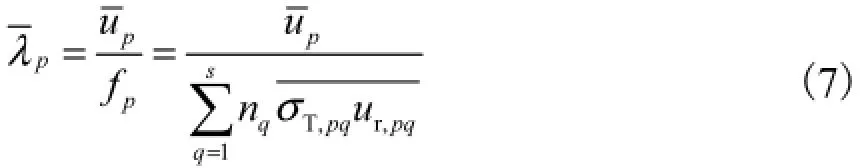
气相空间中混合气体分子的平均自由程[16]则为

式中：n为混合气体的分子数密度，m-3；λ为混合气体分子的平均自由程，m．

2 结果与讨论

2.1 模型验证

实际分子蒸馏过程中，逸出的气体分子间相互碰撞及部分分子在蒸发面或冷凝面再蒸发，使得实际蒸发速率小于由Langmuir-Knudsen公式[6]计算得到的理论蒸发速率．因此，定义分子蒸馏过程一个纯组分的蒸发效率为

Hickman等[7]采用射流张力计对EHP在不同蒸发温度下的蒸发速率进行了实验测定，实验中分子蒸馏器为同轴圆柱的，蒸发面和冷凝面的间距D＝17,mm，冷凝温度TC＝273,K，液相摩尔组成为xEHP＝0.294．分别采用本文模型、文献[8，10]的模型对文献[7]中的EHP-EHS分子蒸馏过程进行模拟计算，并针对相同条件下蒸发效率随蒸发温度的变化情况与实验结果进行了比较，如图2所示．

从图2中可见，本文和文献[8，10]模拟结果及Hickman等[7]的实验结果均发现，蒸发效率随着蒸发温度的升高趋于下降，但会出现小幅度的波动．这是因为蒸发温度升高，蒸发量增大，气相空间分子数密度增大，分子间的碰撞加剧，更多的分子返回蒸发面，蒸发效率降低．另一方面，蒸发温度升高，离开蒸发面的分子法向速度增大，有利于分子向冷凝面运动，蒸发效率会有所提高，因此，蒸发效率出现波动是正常的．而且，文献[8，10]和本文模拟结果与Hickman等[7]实验结果相比，DSMC方法模拟计算的蒸发效率比实验得到的蒸发效率下降速度慢一些．这是因为Hickman等[7]实验采用射流张力计，表面蒸发带走一部分热量，使得下部流体表面温度下降，从而实际蒸发速率减小，实际蒸发效率偏低．

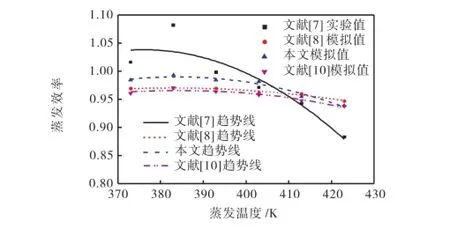
图2 EHP的蒸发效率与蒸发温度的关系Fig.2 Dependence of evaporation efficiency on the evaporator temperature for EHP

由图2可知，不同模型计算的蒸发效率略有不同．本文在考虑分子转动及平动能的同时，采用VHS分子模型计算所得的蒸发效率与Hickman实验值较为接近，相对偏差的绝对平均值为3.57%，而文献[8，10]的HS分子模型计算结果与Hickman等[7]实验值的平均相对偏差分别为4.64%和4.56%．通过以上对比分析可知本文计算模型更接近于实际情况，证明了模型的有效性和模拟结果的可靠性，同时也验证了VHS模型相对于HS模型的优越性．

2.2 蒸发温度的影响

改变蒸发温度，液相分子的蒸发速率将发生变化．这时，气相空间内气体分子数密度和分子之间相对运动速度也相应改变．不同蒸发温度时，x轴上的混合气体分子平均碰撞频率及平均自由程分布的变化关系见图3．其中，冷凝温度TC＝273,K，蒸发面与冷凝面的间距D＝20,mm．

由图3(a)可以看出，混合气体分子的碰撞频率由蒸发面到冷凝面逐渐递减．蒸发温度由353,K升高到373,K时，气相空间同一位置处混合气体分子的碰撞频率增大，整个气相空间的碰撞频率梯度也随蒸发温度的升高而增大．这是因为蒸发温度升高，更多的分子逸出蒸发面进入气相空间，气相空间内气体分子数密度增大，分子之间易发生碰撞，且气体分子的运动速度增大，分子间相对运动速度也随之增大，从而碰撞频率增大．由图3(b)可以看出，平均自由程由蒸发面到冷凝面逐渐递增．蒸发温度升高导致同一位置处的分子平均自由程减小，且蒸发温度提高10,K左右时，整个气相空间平均自由程梯度就明显减小．蒸发温度为353,K时，平均自由程在冷凝面附近达到了最大值，约为5.61,mm．

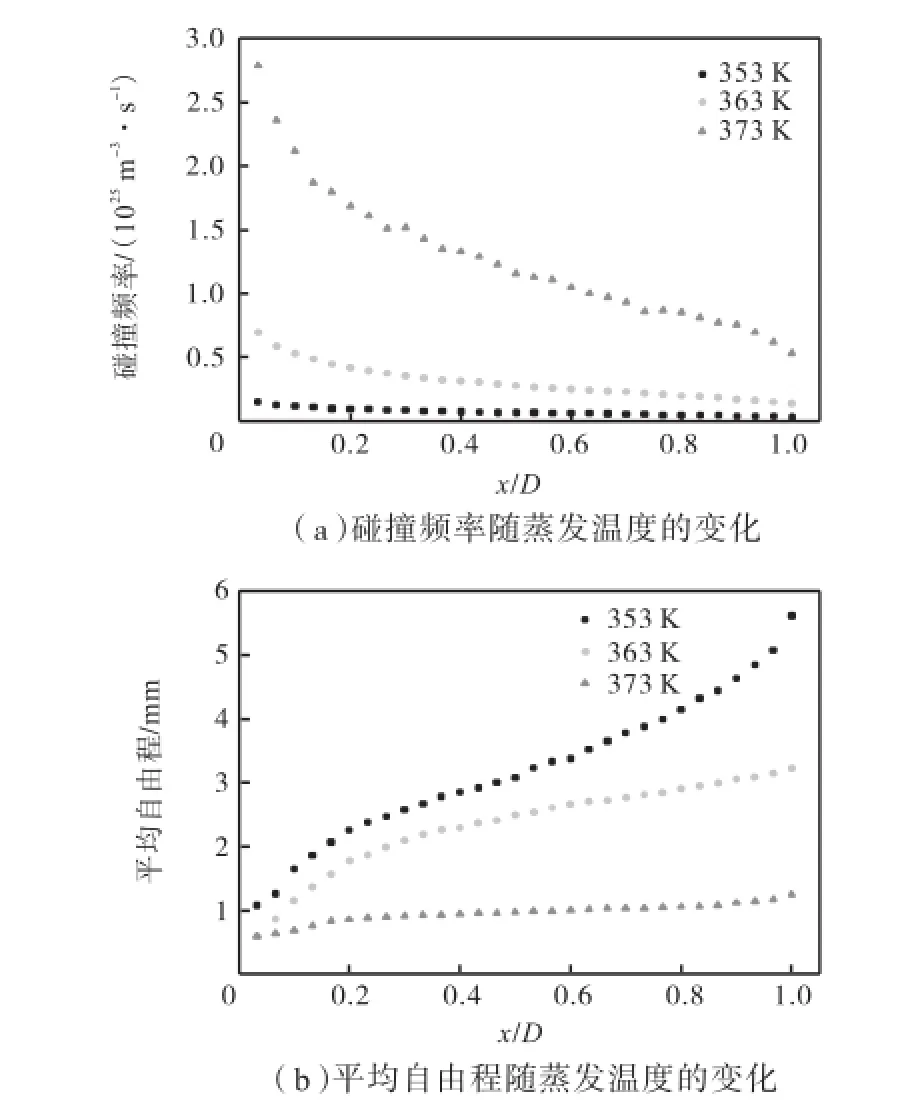
图3 碰撞频率和平均自由程随蒸发温度的变化Fig.3Dependence of collision frequency and mean free path on position at different evaporator temperatures

2.3 冷凝温度的影响

改变冷凝温度，气相分子的冷凝速率将发生变化，这时，气相空间内气体分子数密度和分子间相对运动速度也相应改变．不同冷凝温度时，x轴上的混合气体分子平均碰撞频率及平均自由程分布的变化关系见图4．其中，蒸发温度TE＝353,K，蒸发面与冷凝面的间距D＝20,mm．

从图4(a)和4(b)中可以看出，气相分子运动方向上，即从蒸发面到冷凝面，碰撞频率逐渐降低而平均自由程逐渐增加．冷凝温度升高，碰撞频率呈增大趋势；而平均自由程则是随着冷凝温度的升高呈减小趋势．这主要是因为提高冷凝温度，分子在冷凝面的再蒸发和反射效果加强，使得气相空间内分子数密度相对增大，碰撞分子对的相对运动速度也随之增大，因此，气相空间内碰撞频率增大，相邻两次碰撞之间经过的路程也随之缩短，即分子平均自由程减小．当冷凝温度由273,K升高至293,K时，整个气相空间的分子平均自由程减小，最小值出现在TC＝293,K的蒸发面附近，不足1,mm．

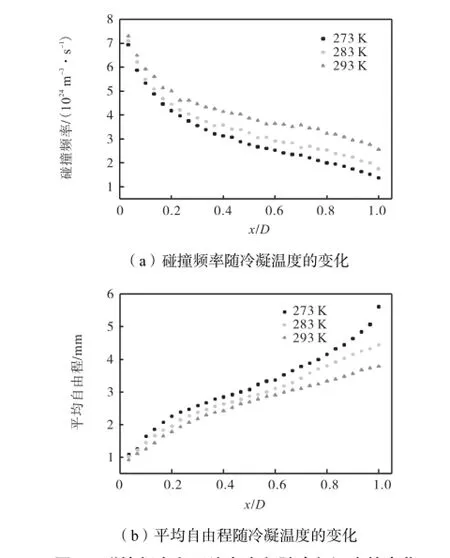
图4 碰撞频率和平均自由程随冷凝温度的变化Fig.4 Dependence of collision frequency and mean free path on position at different condenser temperatures

2.4 蒸发面与冷凝面的间距的影响

改变蒸发面与冷凝面的间距时，气相空间内气体分子数密度和分子间相对运动速度也相应改变．蒸发面与冷凝面的间距不同时，x轴上的混合气体分子平均碰撞频率及平均自由程分布的变化关系见图5．其中，蒸发温度TE＝353,K，冷凝温度TC＝273,K．

从图5(a)中可以看出，碰撞频率由蒸发面到冷凝面是逐渐减小的，且变化梯度也是逐渐减小的．这是因为在靠近蒸发面的地方，分子数密度较大，分子之间发生有频率的剧烈碰撞；而远离蒸发面的地方，分子数密度较小，碰撞作用使得分子的宏观速度增加，分子的无规则运动减弱，平均相对运动速度减小，因此碰撞频率减小．当蒸发面到冷凝面之间的间距增大，整体变化梯度变得平缓．同时，蒸发面附近的分子碰撞频率随着间距增大也增加，冷凝面附近的分子碰撞频率值则越小．由图5(b)可以看出，平均自由程在气体运动方向呈逐渐增大趋势，在冷凝面附近达到最大值．这是因为分子数密度在靠近冷凝面处最小，碰撞不够频繁，分子相对运动速度较小，碰撞频率也最低，相邻两次碰撞之间走过的平均路程也相对最长．蒸发面与冷凝面之间的间距越大，平均自由程变化梯度越平缓．当间距由10,mm增至30,mm时，整个气相空间的平均自由程最大值出现在D＝30,mm时的冷凝面附近，约为5.78,mm，仍不超过此时的蒸馏间距．

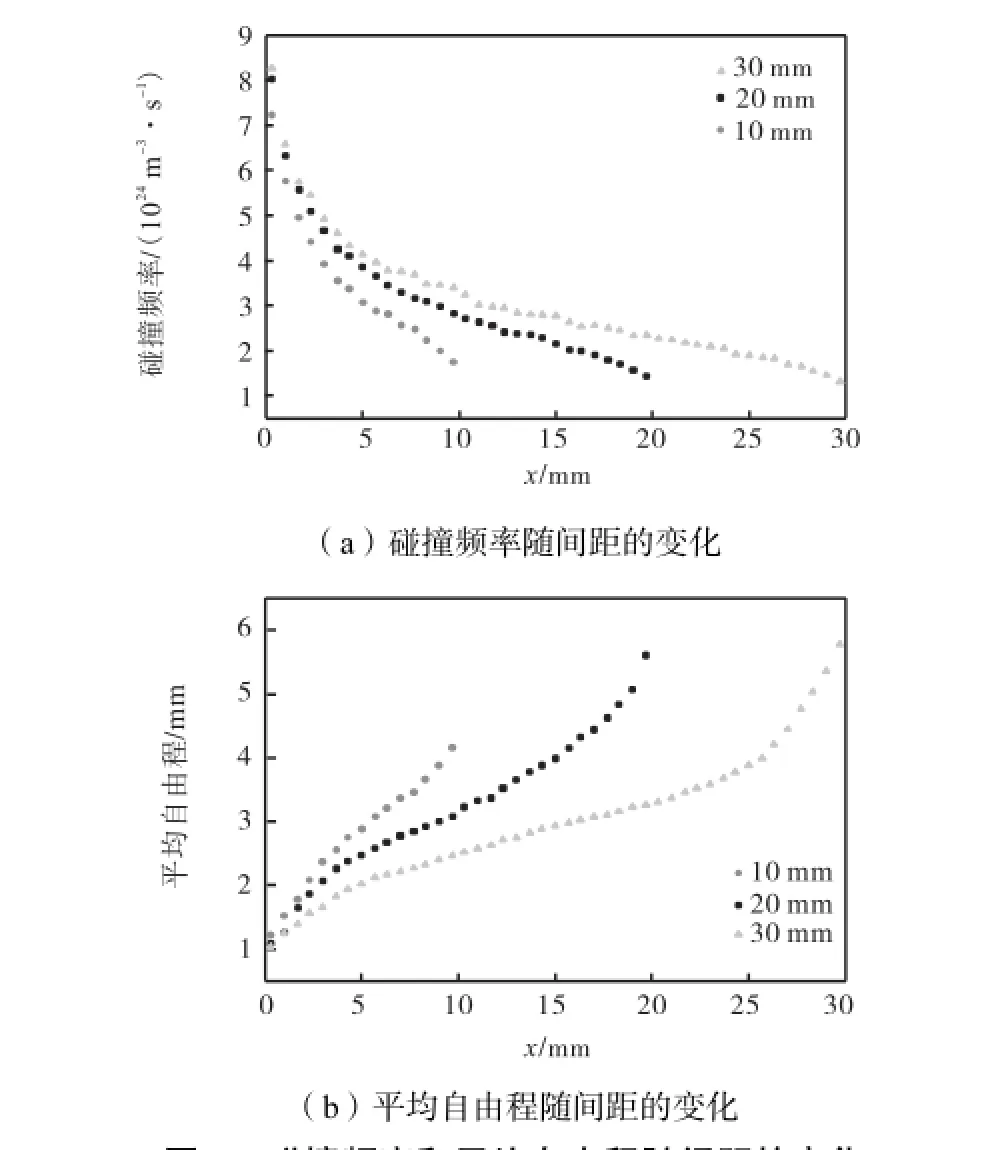
图5 碰撞频率和平均自由程随间距的变化Fig.5Dependence of collision frequency and mean free path on position at different distillation gaps

3 结 论

本文基于DSMC方法，采用更能真实反映气体碰撞过程的VHS模型，同时考虑分子的平动能和转动能，对分子蒸馏气相空间二元分子的碰撞和运动过程进行了模拟，分析了不同操作参数和结构参数对于气相微观特性的影响，填补了分子蒸馏气相传递过程的现有实验和理论分析的不足．蒸发效率的模拟计算结果与文献实验值对比，验证了模型的合理性．通过分析得到如下结论.

(1) 气相空间分子总的碰撞频率和平均自由程始终呈相反的变化趋势．

(2) 在气体分子运动方向上，由蒸发面到冷凝面碰撞频率是逐渐减小的，而平均自由程是逐渐增大的.

(3) 当蒸发温度或冷凝温度升高时，分子蒸馏气相空间同一位置处的碰撞频率增大，平均自由程减小；当蒸发面和冷凝面的间距增大时，碰撞频率也增大，但靠近冷凝面处，间距越大碰撞频率则越小；相反地，平均自由程随着间距增大而减小，在靠近冷凝面处，间距越大分子平均自由程也越大．

［1］ Kaplon J，Kawala Z，Skoczylas A. Evaporation rate of a liquid from the surface of a rotating disc in high vacuum[J]. Chemical Engineering Science，1986，41(3)：519-522.

［2］ Bhandarkar M，Ferron J R. Transport processes in thin liquid films during high-vacuum distillation[J]. Industrial & Engineering Chemistry Research，1988，27(6)：1016-1024.

［3］ Lutišan J，Cvengroš J，Micov M. Heat and mass transfer in the evaporating film of a molecular evaporator [J]. Chemical Engineering Journal，2002，85(2)：225-234.

［4］ 许松林，王 玲，郭 凯．刮膜式分子蒸发器上液体的停留时间分布[J]. 天津大学学报，2012，45(1)：70-74．Xu Songlin，Wang Ling，Guo Kai. Residence time distribution of liquid in wiped film molecular distillation [J]. Journal of Tianjin University，2012，45(1)：70-74(in Chinese).

［5］ Bird G A. Molecular Gas Dynamics and the Direct Simulation of Gas Flow[M]. Oxford：Clarendon Press，1994.

［6］ Bhandarkar M，Ferron J R. Simulation of rarefied vapor flows[J]. Industrial & Engineering Chemistry Research，1991，30(5)：998-1007.

［7］ Hickman K C D，Trevoy D J. Studies in high vacuum evaporation—The falling stream tensimeter [J]. Industrial & Engineering Chemistry，1952，44(8)：1882-1888.

［8］ Lutišan J，Cvengroš J. Mean free path of molecules on molecular distillation[J]. Chemical Engineering Journal， 1995，56(2)：30-50.

［9］ Batistella C B，Maciel M R W，Maciel F R. Rigorous modeling and simulation of molecular distillatory：Development of a simulator under conditions of nonideality of the vapor phase[J]. Computers and Chemical Engineering，2000，24(2)：1309-1315.

［10］ Hu Hui，Huang Jicai，Wu Shuming，et al. Simulation of vapor flows in short path distillation[J]. Computers and Chemical Engineering，2013，49：127-135.

［11］ 吴其芬，陈伟芳. 高温稀薄气体热化学非平衡流动的DSMC方法[M]. 长沙：国防科技大学出版社，1999. Wu Qifen，Chen Weifang. High-Temperature Thermo-Chemical Non-Equilibrium Rarefied Gas Flows DSMC Method [M]. Changsha：National University of Defense Technology Press，1999(in Chinese).

［12］ Boger D，Ozawa T，Zhong J，et al. Modeling of the stardust reentry flows with ionization in DSMC[C]// 45th AIAA Aerospace Science Meeting and Exhibit. Reno，USA，2007：611-634.

［13］ Yaws C L. Chemical Properties Handbook[M]. New York：McGraw-Hill，1999.

［14］ Xubin Z，Chunjian X，Ming Z．Modeling of falling film molecular distillator[J]. Separation Science and Technology，2005，40(6)：1371-1386.

［15］ Tchuen G，Zeitoun D E. Computation of weakly ionized air flow in thermochemical non-equilibrium over spherecones[J]. International Journal of Heat and Fluid Flow，2008，29(5)：1393-1401.

［16］ 吴其芬，陈伟芳，黄 琳，等. 稀薄气体动力学[M].长沙：国防科技大学出版社，2004. Wu Qifen，Chen Weifang，Huang Lin，et al. Rarefied Gas Dynamics[M]. Changsha：National University of Defense Technology Press，2004(in Chinese).

（责任编辑：田 军）

Microscopic Characteristics of Vapors in Molecular Distillation by DSMC Method Based on VHS Molecular Model

Xu Songlin，Li Yang
(School of Chemical Engineering and Technology，Tianjin University，Tianjin 300072，China)

To investigate the microscopic characteristics of vapors in molecular distillation，based on the variable hard sphere(VHS)molecular model，the direct simulation Monte Carlo(DSMC)method was adopted and molecular rotational energy was included as well as molecular translational energy when developing one- and two-dimensional model. The evaporation efficiency at different evaporator temperatures was compared with the published experimental data. The simulated results show a satisfactory agreement with the literature，indicating the simulation model is accurate. The influence of evaporator temperature，condenser temperature and distillation gap on the distribution of collision frequency and the mean free path in vapor space was discussed and analyzed by simulating the movement or collisions between molecules. It is found that the distribution of collision frequency and that of mean free path always show a reverse variation tendency. Near the evaporator surface，collision frequency reaches the maximum value while mean free path reaches the minimum value conversely. Near the condenser surface，the situation is opposite. In the vapor spaces that from the evaporator surface to the condenser surface，collision frequency decreases and the mean free path increases. With the increase of evaporator or condenser temperature，collision frequency in the vapor spaces increases whereas the mean free path decreases at the same location；The collision frequency also increases while the mean free path decreases at the same location with the increase of distillation gap between evaporator and condenser surfaces；Furthermore，the rising distillation gap leads to a smaller mean free path at the same location and a largermean free path near the condenser surface.

molecular distillation；direct simulation Monte Carlo(DSMC) method；variable hard sphere(VHS)；collision frequency；mean free path

TQ028.8

A

0493-2137(2015)11-1023-07

10.11784/tdxbz201406039

2014-06-12；

2014-07-21.

国家自然科学基金资助项目(21176170).

许松林（1966— ），男，博士，副研究员.

许松林，slxu@tju.edu.cn.

时间：2014-10-27. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201406039.html.