基于SAEF方法计算高铁车内全频噪声

毛 杰，郑 旭，郝志勇，孙 强，马晓龙

(1. 浙江大学能源工程学系，杭州 310027；2. 长春轨道客车股份有限公司技术中心，长春 130000)

基于SAEF方法计算高铁车内全频噪声

毛 杰1，郑 旭1，郝志勇1，孙 强2，马晓龙2

(1. 浙江大学能源工程学系，杭州 310027；2. 长春轨道客车股份有限公司技术中心，长春 130000)

提出了统计声学能量流(statistical acoustic energy flow，SAEF)方法，将不同物理场的激励耦合后加载到高铁SAEF模型上，计算车外激励与车内声场及车内声腔之间的声能流动，可分析车内全频噪声．首先，采用刚性多体动力学、快速多极边界元和大涡模拟提取了350,km/h下的轮轨力/二系悬挂力、轮轨噪声和空气动力噪声，并且这些激励通过了参考文献试验的验证．其次，搭建了车厢有限元模型，基于多点激励-多点响应技术验证了车厢仿真模态，证明了整体的车厢及区域的铝型材-内饰组合板的精度，间接保证了基于模态特性的组合板隔声量的准确度．最后，搭建了SAEF模型，加载耦合激励并定义组合板隔声性能后，计算了350,km/h下、0～4,000,Hz内的车内噪声．对比车内中心声腔的仿真与试验声压级，结果显示两者的变化趋势基本一致，声压级总值相差2.6,dB(A)，符合工程要求，验证了SAEF方法应用于高铁车内全频噪声研究的可行性．

高速铁路；全频噪声；统计声学能量流；多物理场耦合激励

高速列车车内声学仿真研究的工作已有很多，主流方法包括有限元-边界元(finite element-boundary element，FE-BE)法、有限元-统计能量分析(finite element-statistical energy analysis，FE-SEA)混合法和统计能量分析(SEA)．各个方法的理论决定了它们的应用范围，例如FE-BE、FE-SEA和SEA分别适用于求解大规模声学问题的低频、中频和高频噪声．

肖友刚等[1]采用FE-BE计算了由轨道不平顺引起的室内低频噪声，但未考虑声激励和内饰件，且由于声学模型自由度和计算量的限制无法求解中高频噪声．Sapena等[2]采用FE-SEA法搭建了驾驶室的中频声学模型，将内饰件等效为吸声系数，考虑了机械力与空气动力噪声的耦合作用，但忽略了轮轨噪声以及内饰件与白车身之间的约束．刘加利等[3]提取了列车表面压力脉动，基于SEA理论分析了车内中高频气动噪声，但未研究其他激励下的车内噪声．需要说明的是高速列车白车身通常为具有夹层结构的铝型材，而SEA子系统为具有夹层属性的单层板，该建模等效过程存在较大误差．此外，上述研究未将分析频域拓宽到全频，结果也未与试验进行对比，很多工作还有待完善．

本文提出了统计声学能量流(statistical acoustic energy flow，SAEF)方法，考虑了完整的多物理场耦合激励，重点研究车外激励与车内声场之间以及车内声腔之间的能量流动，可以快速、准确地预测高铁车内全频噪声．

1 背景理论

列车高速行驶时，引起车内噪声的激励源分为机械激励和声激励两类．机械激励主要指二系悬挂力，它由轮轨力经转向架悬挂系统的衰减产生．声激励分为轮轨噪声、空气动力噪声和设备噪声，由于本文的车厢无受电弓，因此不考虑集电噪声．

1.1 多体动力学理论

车轮与钢轨表面由于存在不平顺性，即粗糙度，在高速行驶时会产生轮轨力．轮轨力通过列车刚性多体动力学获取，计算式[4]为

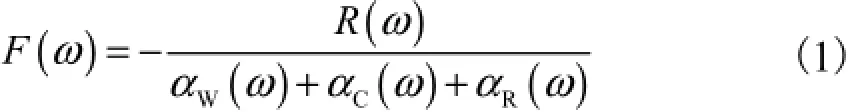
式中：F为垂向轮轨力；ω为圆频率；R为粗糙度；αW、αC和αR分别为车轮、接触弹簧和钢轨的位移导纳(力与位移的比值)．

1.2 轮轨噪声

轮轨力作为一对作用力和反作用力，分别激励车轮和轨道产生振动并辐射噪声．对于钢轨的任一位置z，由轮轨力Fm(ω)作用在zm处引起的振动响应[5]为

式中αRT为钢轨的传递位移导纳．

车轮噪声和轨道噪声通过快速多极边界元分析(fast multi-pole boundary element analysis，FMBEA)获取，采用“分块”原理，可有效求解大规模声学问题[6]．根据边界元理论，已知结构表面振动速度，基于边界条件可计算表面的声压．

1.3 空气动力噪声

高铁的流场速度一般远小于声速(1)Ma≪，因此在车体表面形成的空气动力噪声主要是双极子声源，由外表面的空气压力脉动引起[7]．表面压力脉动及其引起的空气动力噪声分别采用大涡模拟(large-eddy simulation，LES)和间接边界元分析(indirect boundary element analysis，IBEA)获取．

两个强度均为Q、相距I的单极声源组成的双极子声源在空间声场任一位置P(r1，θ1)形成的叠加声压为

式中：ρ为空气密度；c为空气介质中的声速；k为波数，k＝ω/c；θ1为P点到声源中心的连线与极轴的夹角．

1.4 SAEF方法

综合上述理论可以计算各激励源，然后用SAEF方法计算车内噪声，其原理如图1所示．

图1(a)所示为车外噪声经空气传播后在车体表面形成激励的示意，假设图中的声源代表某个车轮.当车轮产生振动并辐射噪声，声波开始向空间传播.根据声学原理，均匀理想流体媒介中具有简谐解的小振幅声波波动的Helmholtz微分方程为

式中：∇2为Laplace算子，∇2＝∂/∂x2＋∂/∂y2＋∂/∂z2；p为声压．

对于振动结构外场声辐射问题，边界条件为Neumann边界条件(给定∂p/∂n)，即

式中：n为法向单位矢量；β、χ、γ为给定参数．

此外，p还必须满足Sommerfeld辐射条件，即

式中：r为声场中的观察点与声源表面的距离；j为虚数单位．

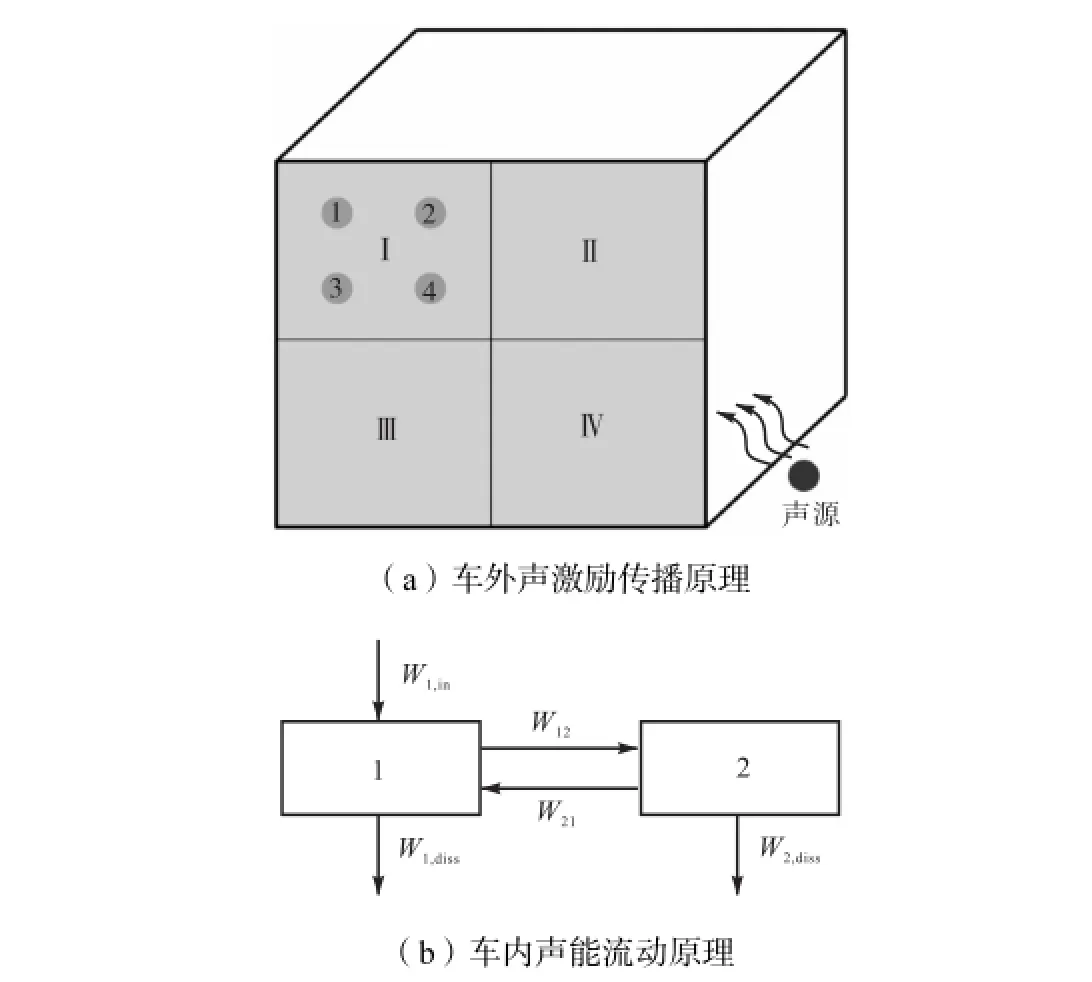
图1 统计声学能量流方法原理Fig.1 Principle of statistical acoustic energy flow method

式中A为待定常数，一般是复数．

观察点对应的径向质点速度为

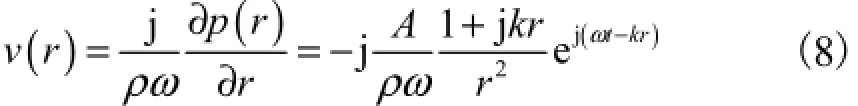
声场中任一位置观察点的声压为

将车体简化为图1(a)中的正方体，并把正面划分为Ⅰ～Ⅳ共4个结构子系统．声波经空气传播后在车体表面形成声学分布，因此在子系统表面布置一定数量的声学观察点，如Ⅰ表面的1～4号观察点，它们的声压和速度分别表示为pI1、pI2、pI3、pI4和vI1、vI2、vI3、vI4，可分别由式(7)和式(8)获取．

观察点1～4对应子系统Ⅰ的面积为SI1、SI2、SI3和SI4，它们与子系统Ⅰ的面积SI之间的关系为

式中：T60为混响时间(声腔内声能量级衰减60,dB所用的时间)；f为频率．

对于一个声腔子系统，除了输入功率与耗散功率以外，剩下的能量来自于子系统之间的流动功率，如图1(b)中所示的W12和W21．这种声功率流动通过声腔之间的耦合损耗因子η12和η21实现，且有

可得子系统Ⅰ表面的车轮噪声声功率W1,w，即

式中*表示共轭复数．

同理可得轨道噪声和空气动力噪声在Ⅰ表面的声功率，将所有声激励耦合后得到Ⅰ上的耦合声功率WI,coup．耦合声功率经Ⅰ的隔声量STL衰减，在车内形成透射声功率WI,in．WI,coup和WI,in的关系为

对于车身铝型材与内饰组合板的隔声量，SEA理论并不是合适的算法，因为无法准确等效铝型材的夹层属性，并且忽略了铝型材与内饰件之间的相互约束，因此本文采用声学有限元法计算组合板的隔声量(详见第3.2节)．在入射侧混响声(1,Pa)的激励下，可以得到组合板透射侧任一位置x的声压p(x)，再通过隔声公式计算组合板的隔声量，即

式中：Γ为组合板有限元模型的表面；G(x，y)为自由场格林函数；y为Γ上的一点．

至此，车体表面的耦合声激励经各结构子系统对应的组合板隔声量衰减，流入到车内声腔子系统的透射声功率已经得到．车内各个声腔子系统之间的声能流动基于SEA理论计算，以两个车内声腔子系统为例，如图1(b)所示．假设声腔子系统1与子结构子系统Ⅰ相连，即W1,in直接输入到声腔1中；声腔2与声腔1相连，但不与任何结构子系统相连，即无外界声能的直接输入．由于声腔存在阻尼损耗因子η，具有耗散功率Wi,diss，且有

式中：Ei为第i个声腔子系统的能量；iη为第i个声腔子系统存在的阻尼损耗因子．

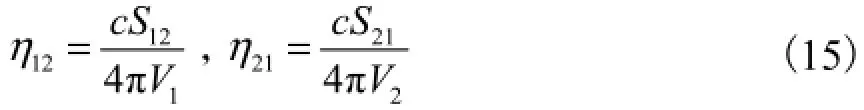
车内声腔的总阻尼损耗因子通过试验测取，其计算式为式中：S12和S21分别为声腔的耦合面积；V1为声腔1的体积；V2为声腔2的体积．

当考虑所有结构子系统流入车内声腔的声功率、以及所有声腔子系统之间的能量流动关系后，即可得到车内任一声腔子系统的声学响应．

2 多物理场激励仿真与试验

2.1 轮轨力与二系悬挂力

如第1节所述，轮轨力和二系悬挂力可通过刚性多体动力学获取，车厢的动力学模型及主要刚体参数分别如图2和表1、表2所示．

在建模过程中，车身等效为刚性质量块，包括重心位置、质量、转动惯量等；转向架等效为轮对、构架、抗蛇行减振器、横向液压减振器、一系悬挂(钢簧)、二系悬挂(空簧)等；由于列车搭载试验在试运营前的京沪线上完成，轮轨粗糙度较小，可以用标准轨道谱简化．

图2 车厢刚性多体动力学模型Fig.2 Rigid multi-body dynamic model of the car

表1 车体的刚体参数Tab.1 Rigid-body parameters of the car body

表2 悬挂弹簧的刚体参数Tab.2 Rigid-body parameters of the suspension springkN/m

350,km/h下、0～4,000,Hz内的垂向轮轨力，如图3(a)所示．轮对左右侧的轮轨力基本一致，整体随频率递减．在1,000,Hz以下有多个峰值，最大超过7,000,N．列车动力学模型是匀速直线行驶，因此沿着轨道和侧向的力暂不考虑．

轮轨力经转向架悬挂系统衰减后，得到空气弹簧悬挂末端的二系悬挂力，如图3(b)所示．二系悬挂力在0～200,Hz内具有较高的峰值，是车内低频噪声的主要激励；在200,Hz以上，二系悬挂力锐减，已不是引起车内噪声的主要因素．考虑到显示效果，本文只给出了0～200,Hz频段的结果．

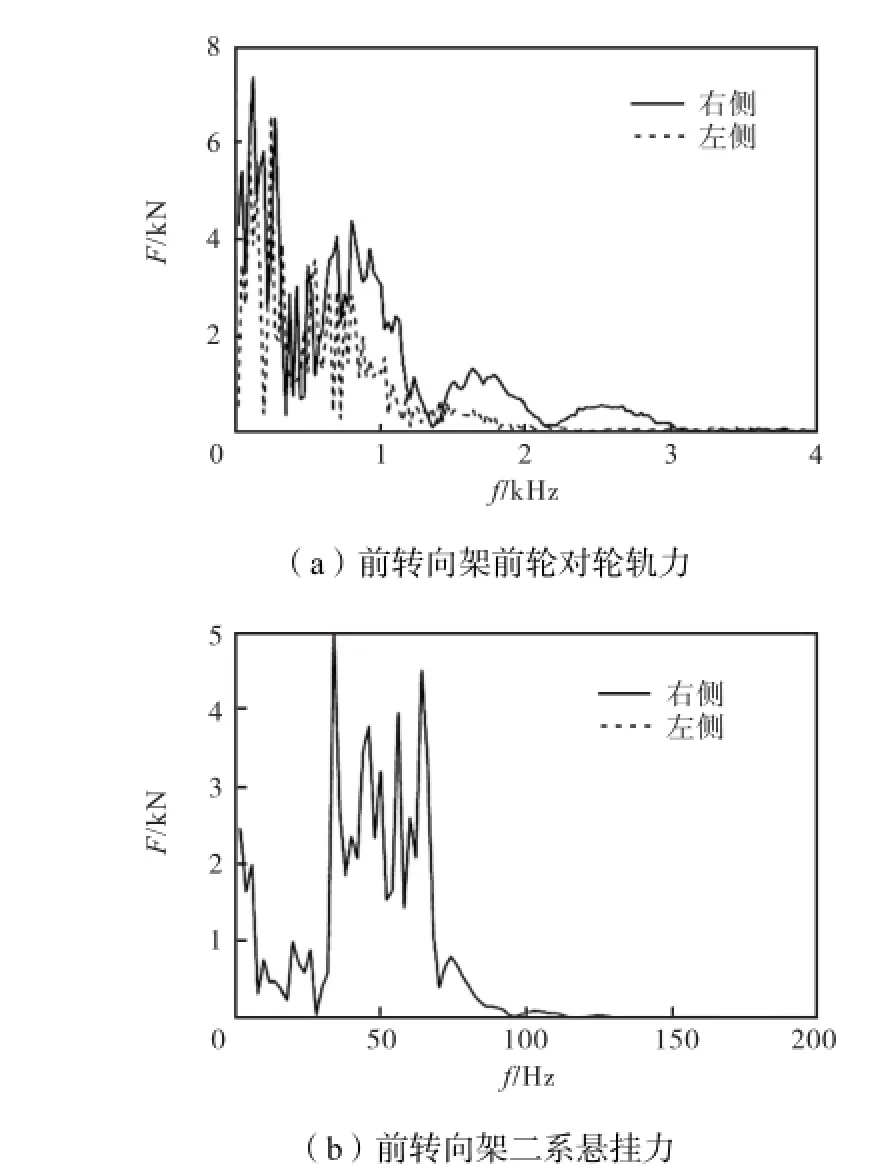
图3 前转向架轮轨力和二系悬挂力Fig.3Wheel-rail interaction force and secondary suspension force of the front bogie

2.2 车外噪声源仿真

车轮噪声经空气介质传播到车体表面的仿真模型如图4(a)所示，包括4个轮对(8个车轮)的结构-声耦合模型和形如车体表面的场点模型．

2.2.6 家乡经济条件 一般家乡经济条件对劳动力外出务工意愿既有正向影响，又有负向影响。一方面，较好的家乡经济条件能够给农村劳动力更宽的视野，使其渴望外出获得更好的就业机会；另一方面，较好的家乡经济条件可能有较好的就业机会，降低其外出务工意愿。调查中，经济条件较差的编码为1，有44名，占22.9%；经济条件一般的编码为2，有92名，占47.9%；经济条件较好的编码为3，有56名，占29.2%。

参考蚌埠-徐州试验路段的轨道结构，搭建了板式轨道有限元模型，包括钢轨、扣件、轨道板、底座和基础梁体，如图4(b)所示．固定钢轨的扣件通常由弹条、预埋铁座、绝缘轨距块和橡胶垫板组成，在计算模型中简化为弹簧-阻尼单元．轨道有限元模型参数如表3所示．

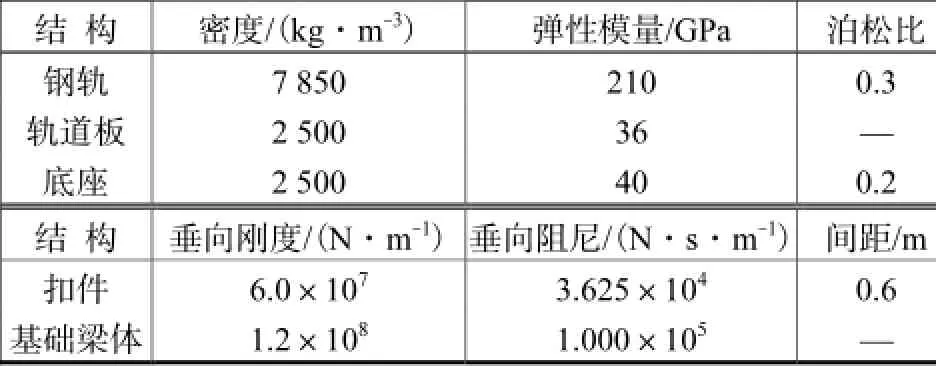
表3 轨道有限元模型参数Tab.3 Parameters of the finite element rail model

计算车体表面的非定常压力脉动所需的全尺寸列车组风洞模型(150,m×18,m×15,m)如图4(a)所示，包括风洞轮廓、进风口、头车、三号车、尾车和出风口，其中头车和尾车的主要作用是保证被试车表面的流场较为顺畅，与实际情况相仿．

选取转向架中心区域的一个声学观察点，得到350,km/h时该点的车轮噪声、轨道噪声和空气动力噪声声压级SPL的1/3倍频程结果，如图4(d)所示，最大峰值分别出现在2,000～2,500,Hz(105,dB)、800～1,000,Hz(106,dB)和1,250～1,600,Hz(106,dB)频段，与Mellet等[8]完成的试验结论基本一致．虽然文献[8]的车型与本文不同，但是头车的转向架与本文具有很高的相似性和参考价值，证明车外噪声源仿真模型和结果的精度．

图4 车外噪声源的仿真模型及结果Fig.4 Simulation models and results of the exterior noise sources

2.3 设备噪声

设备噪声集中在车下设备舱．由于舱内的声源特征复杂，有风扇的旋转噪声、裙板栅栏的空气动力噪声、牵引系统的电磁噪声以及设备的机械噪声等，因此，本文在搭载试验时测取了设备噪声，测点如图5(a)所示．1～3号传声器分别固定在牵引变流器一侧、变流器与冷却风扇电机之间以及冷却风扇电机旁边．各个测点的1/3倍频程声压级结果如图5(b)所示．从图中可以看到，在分析频段内，车下设备舱内的声学环境近似于混响，可以将其简化成混响激励作用在舱内声腔子系统上．

图5 设备噪声测点及结果Fig.5 Measuring points and results of the equipment noise

3 车内全频噪声分析

3.1 统计声学能量流建模

整备车厢有限元模型与SAEF模型之间有密切的关系．在有限元建模时，将车厢划分为3个系统，分别是白车身、内饰件和牵引传动系统．

白车身有限元模型由包含铝型材截面特征的二维四边形单元组成．内饰件从下而上主要包括隔热层、沥水板、吸声层、地板系统、座椅、门窗、木质间壁(洗手间、电气柜等)、玻璃间壁、侧墙板、行李架和通风系统等．牵引系统重点考虑了转向架，并将车下电气设备简化为均布质量施加在白车身模型对应的节点上．整备车厢有限元模型由上述3个系统装配后得到，如图6所示．

图6 整备车厢有限元模型Fig.6 Finite element car model with standard equipment

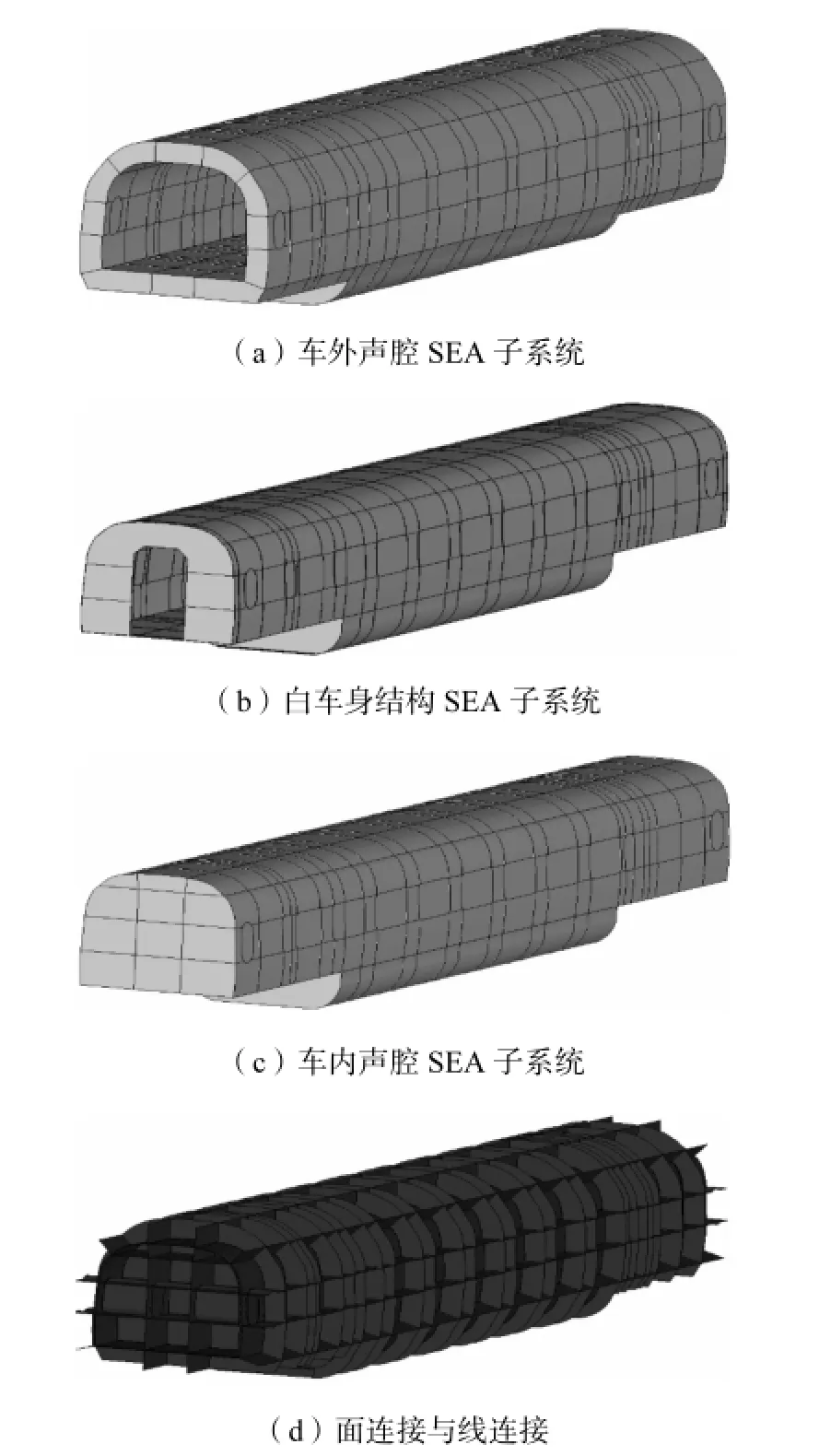
图7 车厢统计声学能量流模型Fig.7 Statistical acoustic energy flow model of the car

3.2 整备车厢隔声性能

车内不同区域的组合板结构不尽相同，对应的隔声量也不一样[8]．从图7(b)中可以看到，白车身结构子系统可以分为3个区域，分别是地板、侧墙和车顶．在每个断面上，3个区域各划分为3个子系统，此外侧墙还包括车窗子系统．其中地板和车窗因构造复杂且隔声性能关键，需要重点研究；其他区域子系统的结构相对简单，分析难度不大．

选取某个区域的地板系统为例，它的有限元模型如图8(a)所示．由于吸音层具有声学特征，需要将其与地板和沥水板的接触面定义为耦合层，与实际情况更加接近．采用声学有限元法计算板件组合板在0～4,000,Hz中心频带内的隔声量，计算模型如图8(b)所示．

板件的隔声性能与模态具有密切的关系，通常在整体模态频率下，板件的隔声曲线易出现低谷．模态分析和隔声试验可以分别间接和直接验证板件隔声性能，但是研究过程中，获取车体各个区域的组合板试件是不现实的，所以需要寻找其他方法验证组合板隔声量的精度．由于组合板是组成整备车厢的子结构，如果整备车厢的有限元模型精度足够高，就能保证子结构的精度，从而间接证明了子结构隔声性能的准确度．

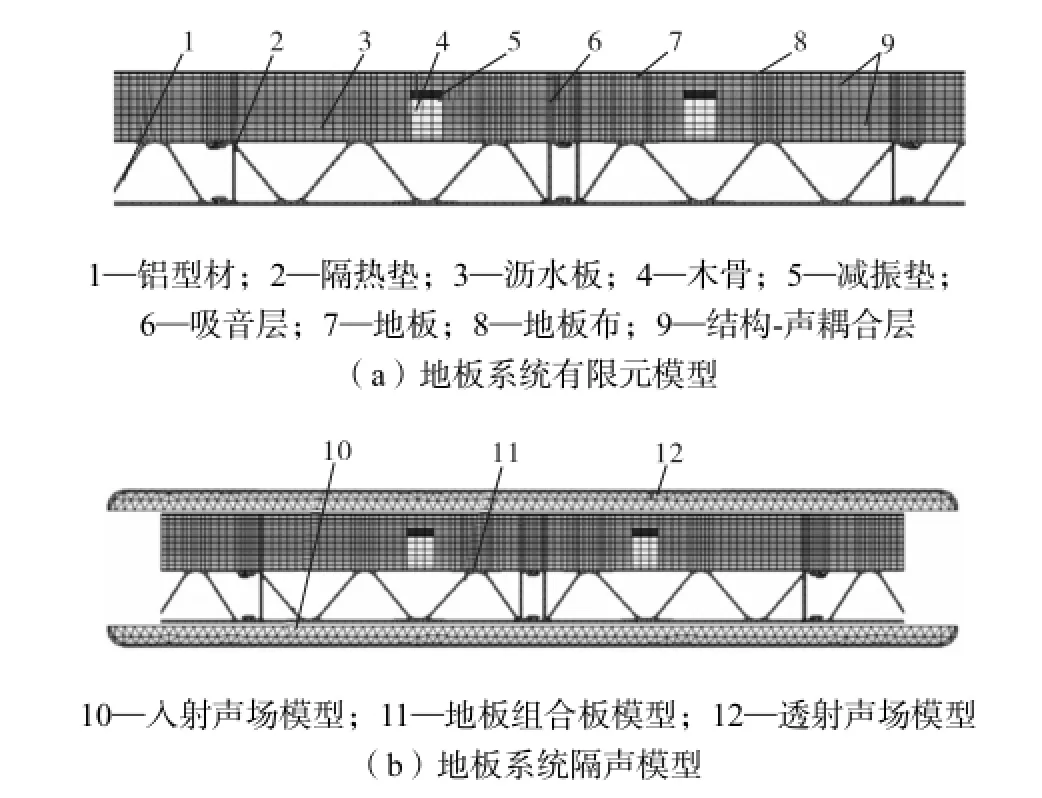
图8 地板组合板结构有限元模型Fig.8 FE model of the floorboard composition structure

整备车厢模态试验采用多点激励-多点响应的测试技术，如图9(a)所示．试验过程中，在车体表面等间距布置振动传感器，测点尽量选取刚度较大的区域．试验时将车厢置于水平轨道上，由于转向架空气弹簧的弹性支撑，车厢近似处于自由边界，并在车下布置多个激振器激励车体并测量模态．

整备车厢首阶垂向弯曲模态对于列车具有重要的意义，具体可参考《200,km/h以上速度级铁道车辆强度设计和试验鉴定暂行规定》．仿真与试验模态振型如图9(b)所示，两者的振型十分一致．由于模态频率为企业的保密内容，故本文无法提供，但两个频率误差在10%以内．综上，整备车厢有限元模型的精度是足够高的，可以间接证明各区域组合板基于模态特性的隔声量仿真结果．

图9 整备车厢首阶垂向弯曲模态振型的仿真与试验对比Fig.9 Simulated and measured first-order vertical bending modal shapes of the car

采用图8(b)的声学有限元模型计算得到该地板系统在0～4,000,Hz频段的隔声量STL，如图10所示．从图中可以看到，该地板组合板的隔声量在总体上随着频率的升高而增大，在1,600,Hz和3,150～4,000,Hz中心频带内出现峰值，隔声量分别为77.9,dB和80.3,dB；但在200,Hz中心频率下出现了隔声量的低谷，因为地板组合板在200,Hz中心频率下具有整体模态，使该频率下出现隔声量低谷．

车窗有限元模型如图11所示，由内外层钢化玻璃、中间空气层和周边的密封橡胶组成．其中，内层和外层的钢化玻璃厚度分别为6,mm和4,mm，空气层厚度为24,mm．空气层和玻璃的接触面定义为流固耦合层．采用声学有限元法计算得到车窗在0～4,000,Hz中心频带内的隔声量，如图10所示．

图10 地板组合板和车窗的隔声量1/3倍频程结果Fig.10 Sound transmission losses of the floorboard composition and window in 1/3 octave band

采用同样的方法得到侧墙上、中、下区域的组合板的隔声量结果，如图12(a)所示．侧墙各区域组合板的隔声量幅值与变化趋势基本一致．然而，由于3个区域的铝型材截面结构相差较大，导致组合板在不同的频率下具有完全不同的模态振型，最终使特定频率下的隔声量出现差异．

车顶区域各组合板子系统的隔声量结果如图12(b)所示．曲线特征与侧墙组合板基本一样．

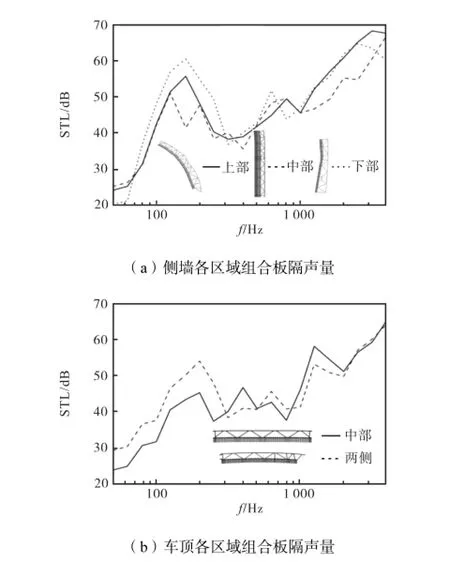
图12 侧墙和车顶组合板的隔声量1/3倍频程结果Fig.12Sound transmission loss of the sidewall and roof composition structure in 1/3 octave band

3.3 车内声学响应仿真与试验对比

将不同区域组合板的隔声性能、机械激励和声激励添加到车厢SAEF模型中，效果如图13所示．

图13 多物理场耦合激励加载到统计声学能量流模型Fig.13 Statistical acoustic energy flow model stimulated by multi-physical field coupling excitation

在开始车内噪声计算之前，还需要基于试验获得一组SAEF模型附属参数，分别是车内声腔的内损耗因子、座椅材料的吸声系数、客室上方的穿孔通风顶板的隔声量和客室两端的玻璃间壁的隔声量．其中，声腔的内损耗因子可以通过式(14)求得，试验结果如图14(a)所示，总体上随频率递减，并在高频处稳定在一个较小的幅值附近．座椅材料的吸声系数通过驻波管测量，结果如图14(a)所示；穿孔顶板和玻璃间壁的隔声量在由混响室和消声室组合的标准隔声实验室测量，结果如图14(b)所示．

图14 统计声学能量流模型附属参数Fig.14 Auxiliary parameters of the SAEF model

计算完成后，得到多物理场激励耦合作用下的车内声腔子系统的声学响应．参考《GB/T 12816—2006铁道客车内部噪声限值及测量方法》，选取车内中心、距离地板1.2,m左右的声腔进行重点研究，得到0～4,000,Hz频段的声压级，与350,km/h下的列车搭载试验相同位置测点的数据对比，结果如图15所示．可以看到，在0～4,000,Hz频段内，车内中心声腔的仿真与试验声压级曲线的趋势总体上保持一致．在100,Hz以下频段，仿真与试验的误差较大，因为组合板的隔声量在低频段受到边界条件的影响. 在1,000,Hz中心频率处，引起仿真与试验误差的主要原因是轨道模型在该频率处的精度不足，使轨道噪声偏大，进而使车内噪声偏大．在其他频率处，仿真与试验的误差总体控制在3,dB以内，满足工程要求．此外，在分析频段内，车内中心声腔的仿真与试验的A计权声压级总值分别为67.6,dB(A)和65.0,dB(A)，相差2.6,dB(A)．

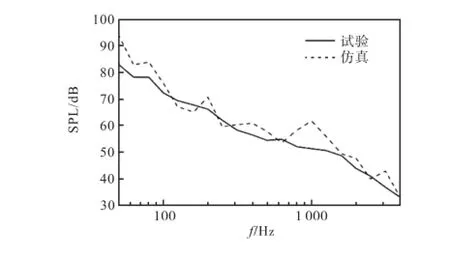
图15 多物理场耦合激励下的车内中心声压级1/3倍频程仿真与试验对比曲线Fig.15Comparison of the 1/3 octave band simulated and measured interior center sound pressure levels under the multi-physical-field coupled excitations

4 结 论

(1) 采用多体动力学、快速多极边界元和大涡模拟提取了350,km/h下的轮轨力/二系悬挂力、车轮噪声、轨道噪声和空气动力噪声，对比文献[9]的试验结果发现，仿真与试验得到的各噪声源最大声能频段一致，对应的声压级误差也较小，验证了多物理场激励的准确性．

(2) 搭建了整备车厢有限元模型，同时完成了车厢的模态试验，得到首阶垂向弯曲模态的仿真与试验结果，两者的频率误差小于10%，且振型高度一致，可以保证模型及组合板隔声性能的精度．

(3) 基于首次提出的SAEF方法计算了350,km/h时多物理场激励下的高速列车车内全频噪声，并对比分析了车内中心声压级的仿真结果与搭载试验结果，误差在工程允许范围内，证明了SAEF方法的可行性和有效性．

［1］ 肖友刚，康志成. 高速列车乘客室内轮轨激励噪声的贡献度分析[J]. 华南理工大学学报：自然科学版，2009，37(2)：98-101，106. Xiao Yougang，Kang Zhicheng. Acoustic contribution analysis of passenger room of high-speed train under wheel-rail excitation[J]. Journal of South China University of Technology：Natural Science Edition，2009，37(2)：98-101，106(in Chinese).

［2］ Sapena J，Tabbal A，Jove J，et al. Interior noise prediction in high-speed rolling stock driver’s cab：Focus on structure-borne paths(mechanical and aero sources) [J]. Noise and Vibration Mitigation for Rail Transportation Systems，2012，118(1)：445-452.

［3］ 刘加利，张继业，张卫华. 高速列车车内中高频气动噪声计算方法[J]. 交通运输工程学报，2011，11(3)：55-60. Liu Jiali，Zhang Jiye，Zhang Weihua. Calculation method of interior aerodynamic noises with middle and high frequencies for high-speed train[J]. Journal of Traffic and Transportation Engineering，2011，11(3)：55-60(in Chinese).

［4］ Thompson D J，Jones C J C. A review of the modelling of wheel/rail noise generation[J]. Journal of Sound and Vibration，2000，231(3)：519-536.

［5］ Wu Tianxing，Thompson D J. Theoretical investigation of wheel/rail non-linear interaction due to roughness excitation[J]. Vehicle System Dynamics，2000，34(4)：261-282.

［6］ Liu Yijun，Nishimura N. The fast multipole boundary element method for potential problems：A tutorial[J]. Engineering Analysis with Boundary Elements，2006，30(5)：371-381.

［7］ Colonius T，Lele S K. Computational aeroacoustics：Progress on nonlinear problems of sound generation[J]. Progress in Aerospace Sciences，2004，40(6)：345-416.

［8］ 张庆辉，郝志勇，张焕宇，等. 柴油机缸盖罩隔声性能与透射噪声[J]. 天津大学学报：自然科学与工程技术版，2014，47(9)：796-802. Zhang Qinghui，Hao Zhiyong，Zhang Huanyu，et al. Sound insulation performance and transmission noise of engine covers of diesel engine[J]. Journal of Tianjin University：Science and Technology，2014，47(9)：796-802(in Chinese).

［9］ Mellet C，Letourneaux F，Poisson F，et al. High speed train noise emission：Latest investigation of the aerodynamic/rolling noise contribution [J]. Journal of Sound and Vibration，2006，293(3/4/5)：525-546.

(责任编辑：孙立华)

Calculation of Full-Spectrum Interior Noise of High-Speed Train with SAEF Method

Mao Jie1，Zheng Xu1，Hao Zhiyong1，Sun Qiang2，Ma Xiaolong2
(1. Department of Energy Engineering，Zhejiang University，Hangzhou 310027，China；2. Research and Development Center，Changchun Railway Vehicles Company Limited，Changchun 130000，China)

Statistical acoustic energy flow(SAEF)method was proposed to study full-spectrum interior noise of highspeed railway trains(HST)，considering multi-physical-field coupling excitations to stimulate the acoustic energy flow between the exterior excitations and interior noise，as well as between the interior acoustic cavities. First of all，rigid multi-body dynamics(RMBD)，fast multi-pole boundary element analysis(FMBEA)and large-eddy simulation(LES)were employed to extract the wheel-rail interaction forces/secondary suspension forces，wheel-rail rolling noise and aerodynamic noise at 350,km/h，respectively；and these excitations were validated by references. Second，a finite element(FE)car model was constructed；the precision of the global FE car as well as the local FE aluminum alloy extrusion-trim part composition boards was validated by modal analysis via multi-input and multioutput technology. Thus，the mode-based sound transmission loss(STL)accuracy of any composition board was indirectly ensured. Finally，the SAEF model of the curb car，which was stimulated by the coupled excitation and defined with the given composite board STLs，was constructed to calculate the interior noise in 0～4,000,Hz at 350,km/h. The simulated and measured interior center sound pressure levels(SPL)were compared. The results show that the variation trend of the simulated 1/3,octave band SPL spectrum agrees well with that of the on-line-measured one. The deviation between the simulated and measured overall SPLs is 2.6,dB(A)，which was well controlled below the engineering tolerance limit，thus validating the feasibility of SAEF method in the HST full-spectrum interior noise analysis.

high-speed train；full-spectrum noise；statistical acoustic energy flow；multi-physical-field couplingexcitation

TB532

A

0493-2137(2015)11-0960-09

10.11784/tdxbz201404101

2014-04-25；

2014-06-12.

国家高技术研究发展计划(863计划)资助项目(2011AA11A103).

毛 杰（1987— ），男，博士研究生，maojie1987@zju.edu.cn.

郑 旭，zhengxu@zju.edu.cn.

时间：2014-07-08. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201404101.html.