一种轴/径向伸缩式成型鼓的运动特性分析

杨玉虎，邬全兵

(天津大学机构理论与装备设计教育部重点实验室，天津 300072)

一种轴/径向伸缩式成型鼓的运动特性分析

杨玉虎，邬全兵

(天津大学机构理论与装备设计教育部重点实验室，天津 300072)

基于我国航空轮胎成型鼓的自主创新需求，针对一种典型的大伸缩比轴/径向伸缩式轮胎成型鼓，研究了其运动特性，以期为该机构的运动学设计奠定基础．基于矢量法建立了该机构的运动学模型，采用无因次分析方法分析了3层鼓肩的运动规律，分别从轴向、径向和周向研究了3层鼓肩依次层叠收缩的相对运动关系，建立了鼓肩避免干涉的几何约束方程．研究结果表明：该成型鼓分2个阶段收缩，鼓肩轴向尺寸越大第1阶段越长；鼓肩的轴向尺寸应小于最大伸展状态下成型鼓轴向尺寸的1/4，否则轴/径向伸缩比减小．最后结合算例对该机构进行了运动学仿真，验证了该分析方法的正确性和有效性．

运动分析；无因次；成型鼓；轴/径向伸缩式

轴/径向伸缩式轮胎成型鼓能同时实现轴向与径向伸缩运动，主要用于航空轮胎等球形轮胎成型．随着我国航空业的发展，航空轮胎的需求量越来越大[1].

成型鼓的轴/径向伸缩比及刚度越大，轮胎的成型范围越大、成型精度越高．国内外研究者基于这两个目标对轴/径向伸缩式成型鼓进行了系统的研究. Artamonova等[2]及Cамохвалов[3]分别提出了一种连杆机构串接齿轮齿条机构来驱动鼓肩实现轴/径向伸缩运动的成型鼓，该种成型鼓对加工及安装精度的要求较高．文献[4-5]提出了两种不同构型的轴/径向伸缩式成型鼓，并对结构与工作原理进行了简单介绍，但并未形成系统的设计理论与方法．杨彦东等[6]提出了一种新型成型鼓并进行了尺度综合，该成型鼓的外瓦鼓肩由相邻两侧完全相同的内瓦连杆机构驱动，在周向形成了闭环结构，整机刚度得到很大提高，但由于成型鼓收缩到最小时形成两层嵌套的圆柱，所以径向伸缩比不大．文献[7]提出的新型成型鼓不仅整机刚度大，而且由于成型鼓收缩到最小时形成3层嵌套的圆柱，所以径向伸缩比更大．但上述文献中，只对特定最大径向与轴向尺寸的成型鼓进行了研究，没有采用无因次分析方法来消除最大径向与轴向尺寸对研究结果的影响，不具有一般性．

本文基于我国航空轮胎成型鼓的自主创新需求，采用无因次分析方法[8-10]分析文献[7]所提出的大伸缩比轴/径向伸缩式轮胎成型鼓的运动特性．首先系统地介绍了该成型鼓的结构与工作原理，并在此基础上建立其运动学模型；其次采用无因次分析方法分析鼓肩的运动规律，建立鼓肩避免干涉的几何约束方程，为该机构的尺度综合奠定了基础．

1 结构与工作原理

根据文献[7]中成型鼓的结构绘制其机构简图，如图1所示．该成型鼓轴向对称．如图1(a)所示，周向由两组构型相同、尺度参数不同的内瓦连杆机构和一组外瓦连杆机构均布而成；如图1(b)所示，Ⅰ为一组内瓦连杆机构，末端连接内层鼓肩；Ⅱ为另一组内瓦连杆机构，末端连接中间层鼓肩；其他均为外瓦连杆机构，末端连接外层鼓肩．内瓦连杆机构由中空轴1、丝杠2、螺母3和3′、主连杆4、副连杆5、内层鼓肩6及内层瓦板7组成；外瓦连杆机构由与主连杆4固联的槽凸轮9、内层鼓肩6、摆杆8、外层鼓肩10及小转臂11组成．

该机构由丝杠2输入运动，驱动螺母3和3′背向运动，进而通过主连杆4和副连杆5导引内层鼓肩6实现轴向与径向收缩运动；中间层鼓肩的运动原理与内层鼓肩相同；相邻两组内瓦连杆机构通过与主连杆固联的凸轮共同导引外层鼓肩实现轴向与径向收缩运动．与内层鼓肩对应的内瓦连杆机构收缩最快，中间层次之，外层最慢，故该成型鼓由最大膨胀工况的单层圆柱面，依次收缩成3层嵌套的圆柱．

为了便于系统地阐述该机构的结构与工作原理，

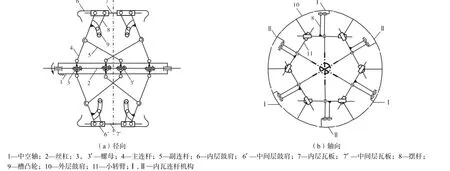
图1 大伸缩比成型鼓机构Fig.1 Building drum mechanism with big telescopic ratio

2 运动分析模型

图2 运动学模型Fig.2 Kinematic model

以丝杠轴线为x轴、轴向对称轴为y轴，建立坐标系Oxy，如图2所示．内层鼓肩对应的连杆机构中，设杆长分别为主连杆的位置角为1ϕ，初始值为10ϕ，摆杆的位置角为1ψ，初始值为10ψ．中间层鼓肩对应连杆机构的参数分别为l21、l22、l23、l24、l25、ϕ2、ϕ20、ψ2和ψ20．

设螺母所在位置点2O与1O的螺距比为k，1O的位移为s，则2O的位移为ks，N的位移为s，M的位移为ks．采用矢量法，分析鼓肩的位移、速度和加速度的变化规律．

2.1 位 移

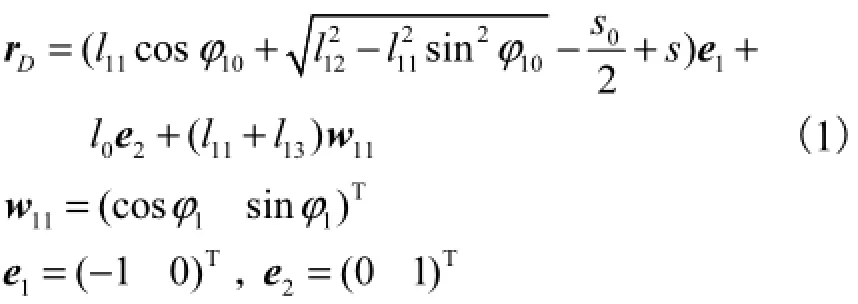
ϕ可在ABC△中由余弦定理得到．

中间层鼓肩上对应点的位置矢量可同理得到．

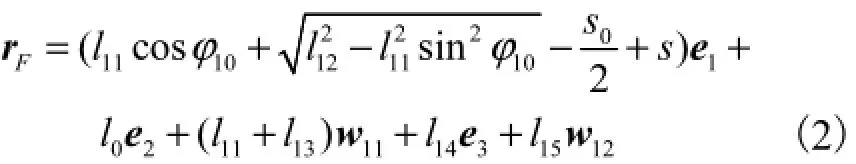
1ψ可由两组相邻的内瓦连杆机构从坐标原点到F点组成的封闭矢量多边形求得，即

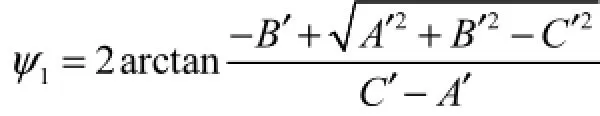
其中

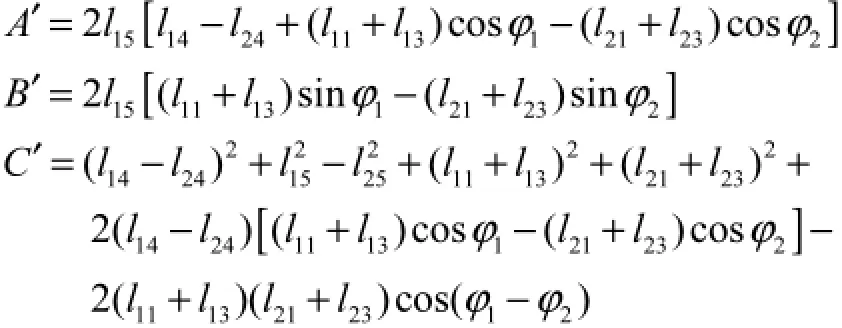
2.2 速 度

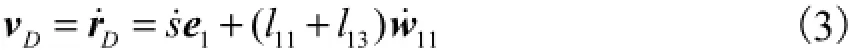
式中

中间层鼓肩上对应点的速度矢量可同理得到．

将F点的位置矢量rF=(xF,yF)T对时间求一阶导数得速度矢量

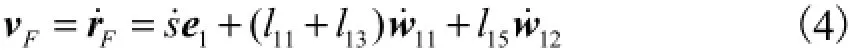
2.3 加速度

将D点的位置矢量rD=(xD,yD)T对时间求二阶导数得加速度矢量

中间层鼓肩上对应点的加速度矢量可同理得到.

将F点的位置矢量rF=(xF,yF)T对时间求二阶导数得加速度矢量如前文所述．

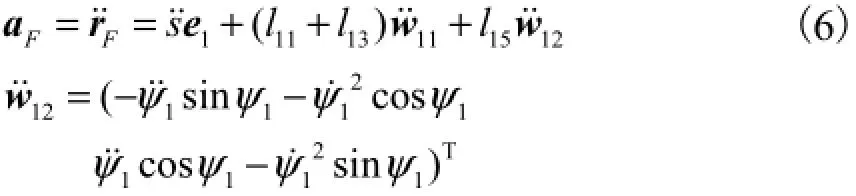
3 运动特性分析

在收缩工况下，首先分析特殊位置处3层鼓肩之间避免几何干涉的条件，然后采用无因次分析方法分析收缩过程中3层鼓肩的运动规律．

3.1 几何约束条件

该鼓是轴向对称结构，对称面同一侧鼓肩的运动规律与另一侧完全相同．在收缩工况下，分别分析同侧3层鼓肩之间的干涉条件及两侧鼓肩之间的干涉条件．鼓肩厚度1Δ和鼓肩轴向尺寸2Δ如图3所示．

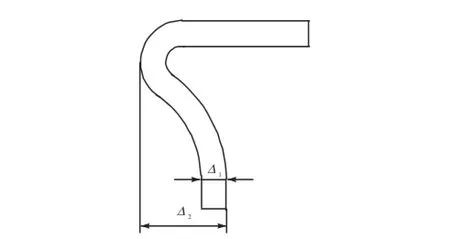
图3 鼓肩结构参数Fig.3 Structural parameters of drum shoulder

3.1.1 同侧内层与中间层鼓肩

如图4所示，同侧内层鼓肩与中间层鼓肩在周向开始层叠时，为了避免发生干涉，它们的轴向位移差需大于鼓肩的厚度．

成型鼓收缩到最小时，为了避免发生干涉，同侧内层鼓肩和中间层鼓肩的轴向位移差需大于鼓肩的轴向尺寸．

3.1.2 同侧中间层与外层鼓肩

如图5所示，中间层鼓肩与外层鼓肩在周向开始层叠时，为了避免发生干涉，它们的径向位移差需大于鼓肩的厚度，且轴向位移差大于鼓肩的轴向尺寸．

成型鼓收缩到最小时，为了增大径向伸缩比，外层鼓肩与中间层鼓肩的径向位移差等于鼓肩的厚度，轴向位移差等于鼓肩的轴向尺寸．

3.1.3 两侧内层鼓肩

为了避免对称面两侧内层鼓肩之间发生干涉，成型鼓收缩到最小时，内层鼓肩不能越过对称面．

需要说明的是，上述分析中，成型鼓收缩到最小时，3层鼓肩的层叠关系是径向伸缩比达到最大的理想结果，但真实机构由于杆件较多，且相邻两内瓦鼓肩之间需要留出空隙以免与外瓦鼓肩上固联的滑块发生干涉，机构并不能收缩到该位置．

3.2 无因次分析

为使分析结果更具有一般性，使其能适用不同尺度的轴/径向伸缩式成型鼓，需消除影响成型鼓运动特性的最大径向及轴向尺寸，如图6所示．为此采用无因次分析方法，设1R=，1H=，在以下分析中横纵坐标分别为无因次量xH和yR．

图4 同侧内层与中间层鼓肩层叠关系Fig.4 Schematic graph of stack-up position of innermost and intermediate drum shoulders

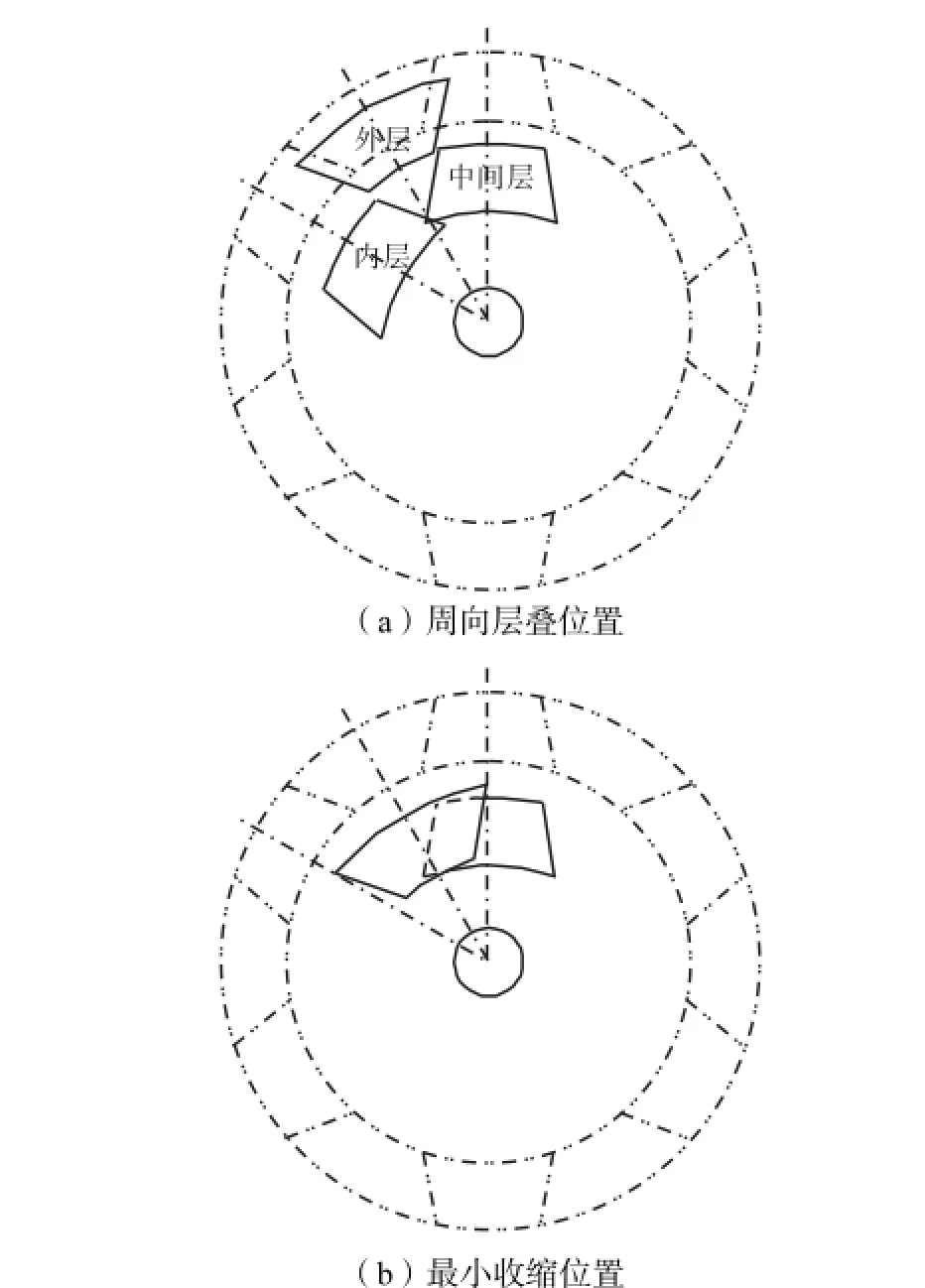
图5 同侧中间层与外层鼓肩层叠关系Fig.5 Schematic graph of stack-up position of intermediate and outermost drum shoulders

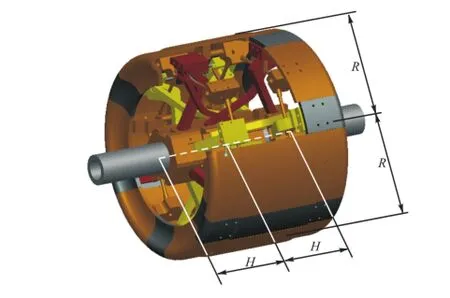
图6 最大径向与轴向尺寸Fig.6 Maximum axial and radial sizes

根据第2节运动分析模型，选取表1和表2所示的机构参数，对3层鼓肩进行运动学仿真．

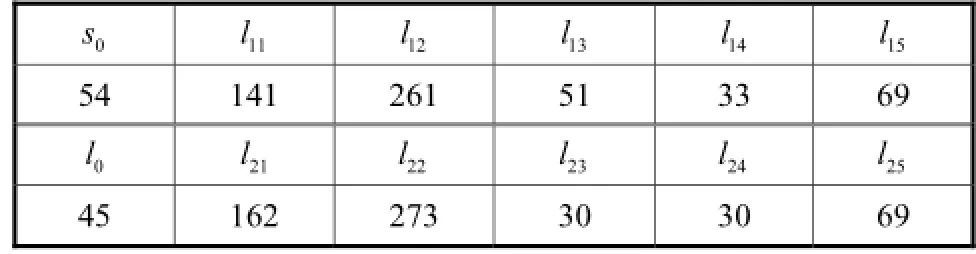
表1 机构主要尺寸参数Tab.1 Main size parameters of the mechanism

表2 机构结构参数Tab.2 Structural parameters of the mechanism

3.2.1 位 移

设螺母都匀速运动，1O处螺母的速率为2,mm/s，由式(1)和式(2)，利用MATLAB编程，计算收缩过程中3层鼓肩的运动轨迹，如图7所示，图中横轴为负值表示所分析的是y轴左侧的鼓肩．

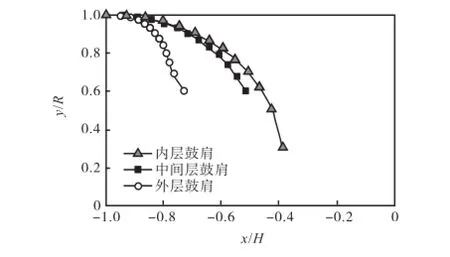
图7 鼓肩运动轨迹Fig.7 Motion trajectories of drum shoulders

为便于比较3层鼓肩的轴/径向位移的大小，采用无因次分析方法，定义成型鼓由最大伸展状态运动到最小收缩状态时，1O处螺母的最大位移为收缩行程，用0S表示．以收缩行程为基准，得3层鼓肩及1O的轴/径向无因次位移．在表1和表2所示机构参数下，取收缩行程为90,mm，由式(1)和式(2)可得3层鼓肩的轴/径向无因次位移随螺母无因次位移的变化曲线如图8所示．下文的螺母都是指1O处螺母．

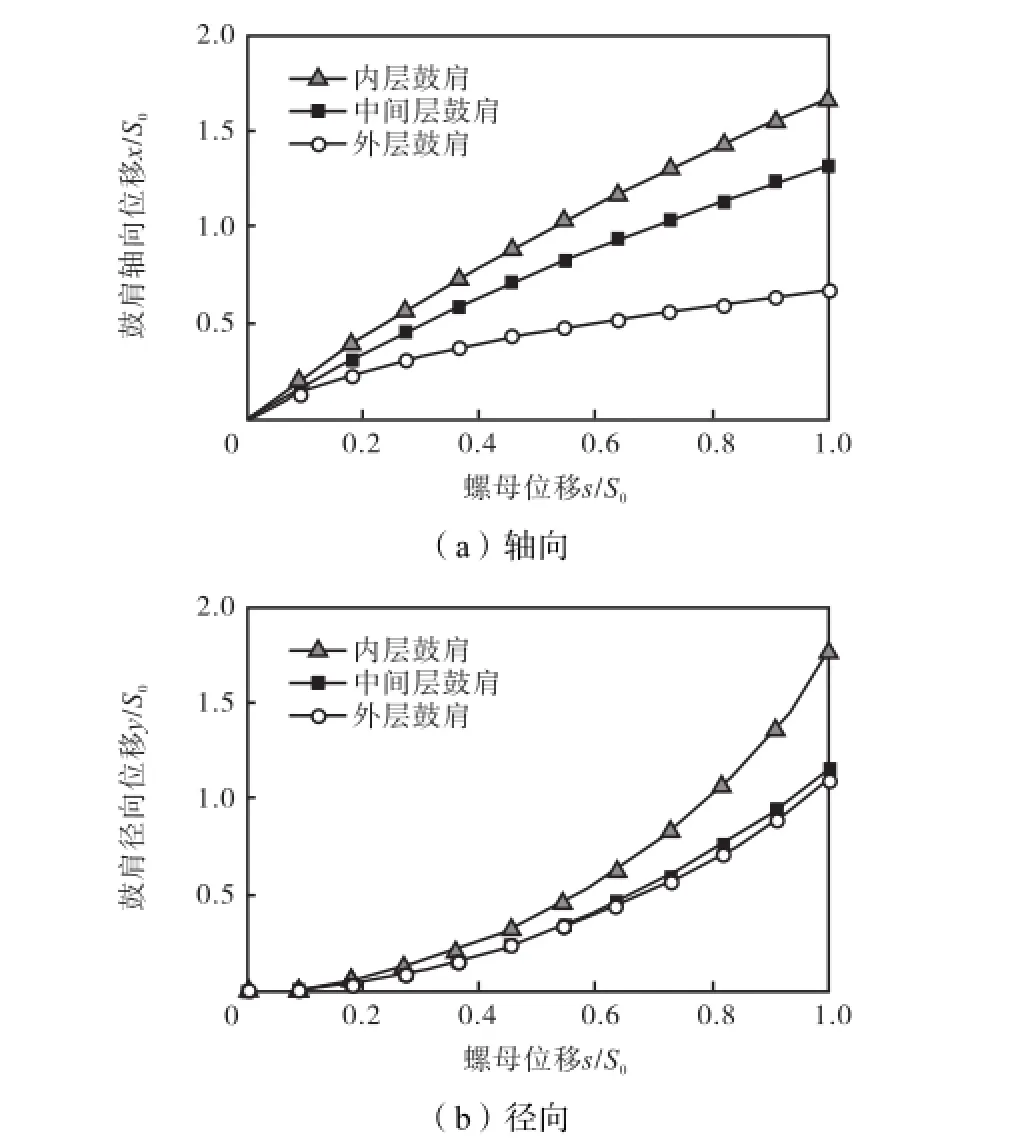
图8 鼓肩位移随螺母位移的变化Fig.8 Displacement of drum shoulders versus nut displacement

由图7和图8可知，成型鼓的收缩过程分为2个阶段．轴向收缩阶段：为避免鼓肩发生干涉，外层鼓肩只沿轴向做收缩运动；轴/径向同时收缩阶段：各层鼓肩沿轴向和径向同时依次做收缩运动．

第3.1节已介绍中间层鼓肩和外层鼓肩之间避免几何干涉的条件，分析可知，鼓肩结构参数1Δ和2Δ是影响第1阶段长度的因素，而参数1Δ相较于2Δ很小，故2Δ是主要影响因素．由轴向约束条件，可得螺母位移随鼓肩结构参数2/HΔ的变化曲线如图9所示.

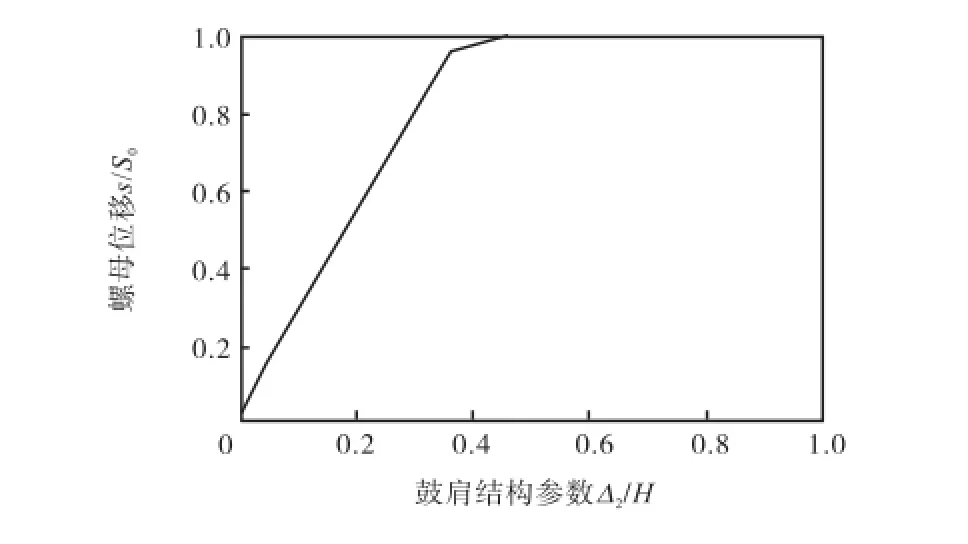
图9 螺母位移随鼓肩结构参数的变化Fig.9Nut displacement versus the structural parameters of drum shoulders

由图9可知，鼓肩结构参数Δ2H 越大，螺母位移越大，即第1阶段越长．当鼓肩结构参数Δ2H =0.5时，成型鼓只有轴向收缩阶段，即中间层鼓肩无法运动到外层鼓肩内部形成嵌套，这会减小成型鼓的轴/径向伸缩比，故鼓肩结构参数应满足Δ2＜0.5H．

3.2.2 速 度

为便于比较3层鼓肩的轴/径向速度的大小，采用无因次分析方法，以螺母的速度为基准，得鼓肩的轴/径向无因次速度．由式(3)和式(4)，利用MATLAB编程，可得3层鼓肩的轴/径向无因次速度随螺母无因次位移的变化曲线，如图10所示．

图10 鼓肩速度随螺母位移的变化Fig.10 Velocity of drum shoulders versus nut displacement

由图10可以看出，外层鼓肩的轴向速度先缓慢减小，在螺母收缩行程结束前快速增大，这利于缩短成型鼓的收缩时间，提高轮胎成型效率；3层鼓肩的径向速度都逐渐增大．

3.2.3 加速度

因为螺母匀速运动，所以鼓肩的加速度不作无因次化处理．由式(5)和式(6)，利用MATLAB编程，可得3层鼓肩的轴/径向无因次加速度随螺母无因次位移的变化曲线，如图11所示．

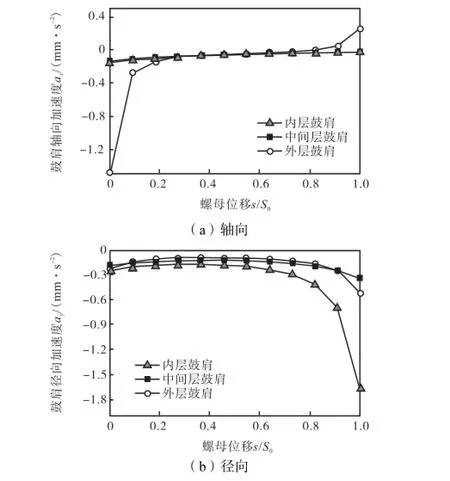
图11 鼓肩加速度随螺母位移的变化Fig.11 Acceleration of drum shoulders versus nut displacement

由图11可以看出，内层鼓肩与中间层鼓肩的轴向加速度很小，而外层鼓肩的轴向加速度先缓慢减小，在收缩行程结束前快速增大，轴向惯性力增大；内层鼓肩的径向加速度先缓慢增大，在收缩行程结束前快速增大，径向惯性力增大．

4 结 论

(1) 成型鼓的收缩过程分为2个阶段．轴向收缩阶段：为避免鼓肩发生干涉，外层鼓肩只沿轴向做收缩运动，且鼓肩轴向尺寸越大第1阶段越长．轴/径向同时收缩阶段：各层鼓肩沿轴向和径向同时依次做收缩运动.

(2) 鼓肩的轴向尺寸应小于最大伸展状态下成型鼓轴向尺寸的1/4，否则会使该种鼓的轴/径向伸缩比减小.

(3) 成型鼓即将收缩到最小之前，受到的轴/径向惯性力快速增大，且径向惯性力主要来自于内层鼓肩，轴向惯性力主要来自于外层鼓肩．

［1］ 王松威，关伟平. 全球航空轮胎业现状与发展趋势[J]. 轮胎工业，2009，29(11)：643-648. Wang Songwei，Guan Weiping. Current conditions and developing tendency of global aircraft tire industry[J]. Tire Industry，2009，29(11)：643-648(in Chinese).

［2］ Artamonova G N，Golovkin E K，Kim V A，et al. Tire-Building Drum：US，4126507[P]. 1978-11-21.

［3］ Cамохвалов Ю И. 大型轮胎成型鼓及其设计方法[J].孙和平，译. 世界橡胶工业，1988(6)：82-86，81. Cамохвалов Ю И. Giant tire building drum and the method of design[J]. Sun Heping，Trans. World Rubber Industry，1988(6)：82-86，81(in Chinese).

［4］ Kawaida S，Kitayama Y. Tire Building Drum：US，4220494[P]. 1980-09-02.

［5］ 谢义忠. 轮胎成型机成型鼓：中国，200620083428. 8[P]. 2006-11-15. Xie Yizhong. Tire Building Drum：China，200620083428. 8[P]. 2006-11-15(in Chinese).

［6］ 杨彦东，杨玉虎. 一种新型轴/径向伸缩式成型鼓及其尺度设计[J]. 天津大学学报，2012，45(12)：1045-1050. Yang Yandong，Yang Yuhu. A new type shaft/radial telescopic tire duilding drum and its dimension design[J]. Journal of Tianjin University，2012，45(12)：1045-1050(in Chinese).

［7］ Roberts C A，Byerley M S. Tire Manufacturing Drum Having Simultaneous Axial and Radial Adjustability：US，6058999[P]. 2000-05-09.

［8］ Cheng C H，Yang H S. Optimization of rhombic drive mechanism used in beta-type Stirling engine based on dimensionless analysis[J]. Energy，2014，64：970-978.

［9］ Tian Y，Shirinzadeh B，Zhang D，et al. Three flexure hinges for compliant mechanism designs based on dimensionless graph analysis[J]. Precision Engineering，2010，34(1)：92-100.

［10］ 虞启辉，石 岩，宋荣志，等. 气动发动机输出扭矩无因次分析[J]. 北京航空航天大学学报，2013，39(9)：1233-1237. Yu Qihui，Shi Yan，Song Rongzhi，et al. Dimensionless analysis of output torque of air-powered engine[J]. Journal of Beijing University of Aeronautics and Astronautics，2013，39(9)：1233-1237(in Chinese).

(责任编辑：金顺爱)

Analysis of Movement Characteristic of an Axial/Radial Telescopic Tire Building Drum

Yang Yuhu，Wu Quanbing
(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China)

Based on the demand for independent innovation of Chinese aircraft tire，a study on the movement characteristics of an axial/radial telescopic tire building drum with big telescopic ratio was conducted，which aimedto lay foundation for kinematic design of the mechanism. Kinematic model of the mechanism was established based on the vector method，and dimensionless analysis was used to analyze the movement rule of drum shoulders. The relative movement of drum shoulders was studied in axial direction，radial direction and circumference respectively，and geometric constraint equations were established to avoid interference. The analysis results show that the building drum has two contraction phases，and the larger the axial size of drum shoulders is，the longer the first phase becomes. The axial size of drum shoulders will be less than a quarter of the axial size of the building drum in the biggest stretch state，otherwise the axial/radial telescopic ratio will decrease. Finally a simulation combined with examples was conducted by MATLAB codes，which shows that the approach is correct and effective.

kinematic analysis；dimensionless；building drum；axial/radial telescopic

TH112

A

0493-2137(2015)11-0947-06

10.11784/tdxbz201406091

2014-07-03；

2014-09-15

国家自然科学基金资助项目(51175367).

杨玉虎（1962— ），男，博士，教授.

杨玉虎，yangyuhu@tju.edu.cn.

时间：2014-09-24. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201406091.html.